IMU 积分的误差状态空间方程推导
文章目录
- 0. 前言
- 1. 离散时间的IMU运动学方程
- 2. 状态变量定义
- 3. 补充公式
- 4. IMU误差状态空间方程推导
0. 前言
本文推导的是 IMU 积分的误差状态空间方程,预积分的推导要比积分复杂,但是推到方法和本文是一样的,因此这里只给出积分的推导方式。
另外,本文的推导方式参考了 R2Live Supplementary Material 中给出的推导,这种方法是基于李群李代数使用 全增量 的方法计算误差状态空间方程,非常好理解。
1. 离散时间的IMU运动学方程
{pi+1=pi+viΔt+12[Ri(ami−bai−nai)−g]Δt2vi+1=vi+[Ri(ami−bai−nai)−g]ΔtRi+1=Riexp[(ωmi−bωi−nωi)Δt]bωi+1=bωi+nbωiΔtbai+1=bai+nbaiΔt\left\{\begin{array}{l} \mathbf{p}_{i+1}=\mathbf{p}_i+\mathbf{v}_i \Delta t+\frac{1}{2}\left[\mathbf{R}_i\left(\mathbf{a}_{m i}-\mathbf{b}_{a_i}-\mathbf{n}_{a i}\right)-\mathbf{g}\right] \Delta t^2 \\ \mathbf{v}_{i+1}=\mathbf{v}_i+\left[\mathbf{R}_i\left(\mathbf{a}_{m i}-\mathbf{b}_{a i}-\mathbf{n}_{a i}\right)-\mathbf{g}\right] \Delta t \\ \mathbf{R}_{i+1}=\mathbf{R}_i \exp \left[\left(\mathbf{\omega}_{mi}-\mathbf{b}_{\omega i}-\mathbf{n}_{\omega i}\right) \Delta t\right] \\ \mathbf{b}_{\omega i+1}=\mathbf{b}_{\omega i}+\mathbf{n}_{b_\omega i} \Delta t \\ \mathbf{b}_{a_i+1}=\mathbf{b}_{a i}+\mathbf{n}_{b_a i} \Delta t \end{array}\right. ⎩⎨⎧pi+1=pi+viΔt+21[Ri(ami−bai−nai)−g]Δt2vi+1=vi+[Ri(ami−bai−nai)−g]ΔtRi+1=Riexp[(ωmi−bωi−nωi)Δt]bωi+1=bωi+nbωiΔtbai+1=bai+nbaiΔt
- 式中忽略了参考坐标系,一般可以选择 worldworldworld 系 W{W}W,此时 g=[0,0,9.8]Tg=[0, 0, 9.8]^Tg=[0,0,9.8]T;
- nai,nωi\mathbf{n}_{a i},\mathbf{n}_{\omega i}nai,nωi 为IMU读数的高斯白噪声;
- nbai,nbωi\mathbf{n}_{b_a i},\mathbf{n}_{b_\omega i}nbai,nbωi 为IMU零偏的随机游走的高斯分布。
2. 状态变量定义
- 名义状态 x^\hat{\mathbf{x}}x^:估计出来的状态,真正能算出来的状态;
- 真实状态 x\mathbf{x}x:无法计算出来的状态,永远不知道的状态,只能用公式表示出来;
- 误差状态 δx\mathbf{\delta x}δx:真实状态 x\mathbf{x}x 与 名义状态 x^\hat{\mathbf{x}}x^ 的差值,关系式为:x=x^+δx\mathbf{x} = \hat{\mathbf{x}} + \mathbf{\delta x}x=x^+δx,即 真实状态 = 名义状态 + 误差状态。
比如:
-
角速度 ω\mathbf{\omega}ω 的名义状态和真实状态:
{名义值:ωi^=ωmi−b^ωi真实值:ωi=ωi^−δb^ωi−nωi=ωmi−b^ωi−δb^ωi−nωi\left\{\begin{array}{l} 名义值:\hat{\mathbf{\omega}_i} = \mathbf{\omega}_{m i} - \hat{\mathbf{b}}_{\omega i} \\ 真实值:\mathbf{\omega}_i = \hat{\mathbf{\omega}_i} - \delta\hat{\mathbf{b}}_{\omega i} - \mathbf{n}_{\omega i} = \mathbf{\omega}_{m i} - \hat{\mathbf{b}}_{\omega i} - \delta\hat{\mathbf{b}}_{\omega i} - \mathbf{n}_{\omega i} \end{array}\right. {名义值:ωi^=ωmi−b^ωi真实值:ωi=ωi^−δb^ωi−nωi=ωmi−b^ωi−δb^ωi−nωi -
加速度 a\mathbf{a}a 的名义状态和真实状态:
{名义值:ai^=ami−b^ai真实值:ai=ai^−δb^ai−nai=ami−b^ai−δb^ai−nai\left\{\begin{array}{l} 名义值:\hat{\mathbf{a}_i} = \mathbf{a}_{m i} - \hat{\mathbf{b}}_{a i} \\ 真实值:\mathbf{a}_i = \hat{\mathbf{a}_i} - \delta\hat{\mathbf{b}}_{a i} - \mathbf{n}_{a i} = \mathbf{a}_{m i} - \hat{\mathbf{b}}_{a i} - \delta\hat{\mathbf{b}}_{a i} - \mathbf{n}_{a i} \end{array}\right. {名义值:ai^=ami−b^ai真实值:ai=ai^−δb^ai−nai=ami−b^ai−δb^ai−nai
3. 补充公式
-
李代数上的增量和李群上的扰动之间的关系:
exp(ϕ+Δϕ)=exp(JlΔϕ)⋅exp(ϕ)=exp(ϕ)⋅exp(JrΔϕ)\begin{align} \exp (\phi+\Delta \phi) =\exp (J_l \Delta \phi) \cdot \exp (\phi) =\exp (\phi) \cdot \exp (J_r \Delta \phi)\end{align} exp(ϕ+Δϕ)=exp(JlΔϕ)⋅exp(ϕ)=exp(ϕ)⋅exp(JrΔϕ) -
SO(3)SO(3)SO(3)的伴随性质:
R⊤exp(ϕ)R=exp(R⊤ϕ)\begin{align}R^{\top} \exp (\phi) R=\exp \left(R^{\top} \phi\right)\end{align} R⊤exp(ϕ)R=exp(R⊤ϕ) -
BCH近似公式:
log[exp(ϕ1)exp(ϕ2)]={Jl(ϕ2)−1ϕ1+ϕ2,ϕ1≈0Jr(ϕ1)−1ϕ2+ϕ1,ϕ2≈0\begin{align} \log \left[\exp \left(\phi_1\right) \exp \left(\phi_2\right)\right]=\left\{\begin{array}{l}\operatorname{J_l}\left(\phi_2\right)^{-1} \phi_1+\phi_2, \quad \phi_1 \approx 0 \\ \operatorname{J_r}\left(\phi_1\right)^{-1} \phi_2+\phi_1, \quad \phi_2 \approx 0 \end{array}\right.\end{align} log[exp(ϕ1)exp(ϕ2)]={Jl(ϕ2)−1ϕ1+ϕ2,ϕ1≈0Jr(ϕ1)−1ϕ2+ϕ1,ϕ2≈0
4. IMU误差状态空间方程推导
4.1. 旋转误差 δr^i+1\delta\hat{\mathbf{r}}_{i+1}δr^i+1
定义:δr^i+1=log[R^i+1⊤Ritt]名义值:R^i+1=R^iexp(w^iΔt)真实值:Ri+1=R^iexp(δr^i)⋅exp(ωiΔt)\begin{aligned} \text { 定义:} \delta \hat{r}_{i+1} & =\log \left[\hat{R}_{i+1}^{\top} R_{i t t}\right] \\ \text {名义值:} \hat{R}_{i+1} & =\hat{R}_i \exp \left(\hat{w}_i \Delta t\right) \\ \text {真实值:} R_{i+1} & =\hat{R}_i \exp \left(\delta \hat{r}_i\right) \cdot \exp \left(\omega_i \Delta t\right) \end{aligned} 定义:δr^i+1名义值:R^i+1真实值:Ri+1=log[R^i+1⊤Ritt]=R^iexp(w^iΔt)=R^iexp(δr^i)⋅exp(ωiΔt)
则旋转误差如下:

4.2. 速度误差 δv^i+1\delta\hat{\mathbf{v}}_{i+1}δv^i+1
名义值:v^i+1=v^i+(R^ia^i−g)Δt真实值:vi+1=(v^i+δv^i)+[R^iexp(δr^i)(a^i−δb^ai−nai)−g]Δt\begin{aligned} 名义值: \hat{v}_{i+1}&=\hat{v}_i+\left(\hat{R}_i \hat{a}_i-g\right) \Delta t \\ 真实值:v_{i+1} &= \left(\hat{v}_i+\delta \hat{v}_i \right) + \left[\hat{R}_i \exp \left(\delta \hat{r}_i\right)\left(\hat{a}_i-\delta \hat{b}_{a i}-n_{a i}\right)-g\right] \Delta t \end{aligned} 名义值:v^i+1真实值:vi+1=v^i+(R^ia^i−g)Δt=(v^i+δv^i)+[R^iexp(δr^i)(a^i−δb^ai−nai)−g]Δt

4.3. 平移误差 δpi+1\delta \mathbf{p}_{i+1}δpi+1
名义值: p^i+1=pi^+v^iΔt+12(Ri^ai^−g)Δt2真实值: pi+1=(p^i+δp^i)+(v^i+δv^i)Δt+12[R^i⋅exp(δr^i)(a^i−δb^ai−nai)−g]⋅Δt2\begin{aligned} & \text { 名义值: } \hat{p}_{i+1}=\hat{p_i}+\hat{v}_i \Delta t+\frac{1}{2}\left(\hat{R_i} \hat{a_i}-g\right) \Delta t^2 \\ & \text { 真实值: } p_{i+1}=\left(\hat{p}_i+\delta \hat{p}_i\right)+\left(\hat{v}_i+\delta \hat{v}_i\right) \Delta t+\frac{1}{2}\left[\hat{R}_i \cdot \exp \left(\delta \hat{r}_i\right)\left(\hat{a}_i-\delta \hat{b}_{ai}-n_{ai}\right) -g\right] \cdot \Delta t^2 \\ & \end{aligned} 名义值: p^i+1=pi^+v^iΔt+21(Ri^ai^−g)Δt2 真实值: pi+1=(p^i+δp^i)+(v^i+δv^i)Δt+21[R^i⋅exp(δr^i)(a^i−δb^ai−nai)−g]⋅Δt2

4.4. 角速度零偏误差 δb^wi+1\delta \hat{b}_{w_{i+1}}δb^wi+1
名义值:b^wi+1=b^wi真实值:bwi+1=b^wi+δbwi+Δt⋅nbwi误差:δbwi+1=δbwi+Δt⋅nbwi\begin{aligned} \text { 名义值:} \hat{b}_{w_{ i+1}} &=\hat{b}_{w i} \\ \text { 真实值:} b_{w_{i+1} } &=\hat{b}_{w_i}+\delta b_{w i}+\Delta t \cdot n_{b_{wi}} \\ \text { 误差:} \delta b_{w_{i+1} } &=\delta b_{w i}+\Delta t \cdot n_{b_{wi}} \\ \end{aligned} 名义值:b^wi+1 真实值:bwi+1 误差:δbwi+1=b^wi=b^wi+δbwi+Δt⋅nbwi=δbwi+Δt⋅nbwi
4.5. 加速度零偏误差 δb^ai+1\delta \hat{b}_{a_{i+1}}δb^ai+1
名义值:b^ai+1=b^ai真实值:bai+1=b^ai+δbai+Δt⋅nbai误差:δbai+1=δbai+Δt⋅nbai\begin{aligned} \text { 名义值:} \hat{b}_{a_{ i+1}} &=\hat{b}_{a i} \\ \text { 真实值:} b_{a_{i+1} } &=\hat{b}_{a_i}+\delta b_{a i}+\Delta t \cdot n_{b_{ai}} \\ \text { 误差:} \delta b_{a_{i+1} } &=\delta b_{a i}+\Delta t \cdot n_{b_{ai}} \\ \end{aligned} 名义值:b^ai+1 真实值:bai+1 误差:δbai+1=b^ai=b^ai+δbai+Δt⋅nbai=δbai+Δt⋅nbai
4.6. 整理成矩阵状态空间方程的形式
定义IMU运动学的矩阵状态空间方程形式为
δx^i+1=Fx⋅δx^i+Fw⋅wi\delta \hat{\mathbf{x}}_{i+1}=\mathbf{F}_x \cdot \delta \hat{\mathbf{x}}_i + \mathbf{F}_w \cdot \mathbf{w}_i δx^i+1=Fx⋅δx^i+Fw⋅wi
其中状态变量的定义为:
δx^i=[δr^i,δp^i,δv^i,δb^wi,δb^ai]⊤wi=[δnwi,δnai,δnbwi,δnbai]⊤\begin{aligned} \delta \hat{\mathbf{x}}_i &= \left[\delta \hat{\mathbf{r}}_i, ~~\delta \hat{\mathbf{p}}_i, ~~\delta \hat{\mathbf{v}}_i, ~~\delta \hat{\mathbf{b}}_{wi}, ~~\delta \hat{\mathbf{b}}_{ai}\right]^{\top} \\ \mathbf{w}_i &= \left[\delta\mathbf{n}_{wi}, ~~\delta\mathbf{n}_{ai}, ~~\delta\mathbf{n}_{b_{wi}}, ~~ \delta\mathbf{n}_{b_{ai}}\right]^{\top} \end{aligned} δx^iwi=[δr^i, δp^i, δv^i, δb^wi, δb^ai]⊤=[δnwi, δnai, δnbwi, δnbai]⊤
则系数矩阵为:
Fx=[exp(−ωiΔt^)00−IΔt00IIΔt00−R^i(a^i)×Δt0I0−R^iΔt000I000000]Fω=[−IΔt00000000−R^iΔt0000IΔt0000IΔt]\begin{aligned} \mathbf{F}_x &= \left[\begin{array}{ccccc} \exp \left(-\hat{\omega_i \Delta t}\right) & 0 & 0 & -I \Delta t & 0 \\ 0 & I & I \Delta t & 0 & 0\\ -\hat{R}_i\left(\hat{a}_i\right)_{\times} \Delta t & 0 & I & 0 & -\hat{R}_i \Delta t \\ 0 & 0 & 0 & I & 0 \\ 0 & 0 & 0 & 0 & 0 \end{array}\right] \\\\ F_\omega &=\left[\begin{array}{cccc} -I \Delta t & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & -\hat{R}_i \Delta t & 0 & 0 \\ 0 & 0 & I \Delta t & 0 \\ 0 & 0 & 0 & I \Delta t \end{array}\right] \end{aligned} FxFω=exp(−ωiΔt^)0−R^i(a^i)×Δt000I0000IΔtI00−IΔt00I000−R^iΔt00=−IΔt000000−R^iΔt00000IΔt00000IΔt
协方差矩阵的传播公式为:
Pi+1=FxPiFx⊤+FωQFω⊤\mathbf{P}_{i+1}=\mathbf{F}_x \mathbf{P}_i \mathbf{F}_x{ }^{\top}+\mathbf{F}_\omega \mathbf{Q} \mathbf{F}_\omega{ }^{\top} Pi+1=FxPiFx⊤+FωQFω⊤
其中 Q\mathbf{Q}Q 为测量噪声的协方差矩阵。
相关文章:

IMU 积分的误差状态空间方程推导
文章目录0. 前言1. 离散时间的IMU运动学方程2. 状态变量定义3. 补充公式4. IMU误差状态空间方程推导4.1. 旋转误差 δr^i1\delta\hat{\mathbf{r}}_{i1}δr^i14.2. 速度误差 δv^i1\delta\hat{\mathbf{v}}_{i1}δv^i14.3. 平移误差 δpi1\delta \mathbf{p}_{i1}δpi14.4. …...

VirtualBox的克隆与复制
快照太多,想整合成1个文件怎么办? 最近,我就遇到一个问题。快照太多了。比较占用空间怎么办? 错误做法 一开始,我是这么操作的,选中某个快照,然后选择删除…然后我登录虚拟机后,发…...

每天5分钟玩转机器学习算法:逆向概率的问题是什么?贝叶斯公式是如何解决的?
本文重点 前面我们已经知道了贝叶斯公式,以及贝叶斯公式在机器学习中的应用,那么贝叶斯公式究竟解决了一个什么样的问题呢?贝叶斯是为了解决逆向概率的问题。 正向的概率和逆向的概率 正向概率:假设袋子里面有N个白球,有M个黑球,你伸手一摸,那么问题就是你摸出黑球的概…...

游戏闲聊之游戏是怎么赚钱的
其实一般情况下不太爱写这种文章,简单说就一点,这个行业的人我惹不起。 1、外挂 所谓外挂,是指通过技术手段,提供辅助游戏的工具,方便玩家获得一些额外的能力; 这事我特意咨询过律师,外挂分两…...
Redis高频面试题汇总(下)
目录 1.Redis中什么是Big Key(大key) 2.Big Key会导致什么问题 3.如何发现 bigkey? 4.为什么redis生产环境慎用keys *命令 5.如何处理大量 key 集中过期问题 6.使用批量操作减少网络传输 7.缓存穿透 8.缓存击穿 9.缓存雪崩 10.缓存污染(或满了…...
Windows修改Docker安装目录修改Docker镜像目录,镜像默认存储位置存放到其它盘
Windows安装Docker,默认是安装在C盘,下载镜像后会占用大量空间,这时需要调整镜像目录;场景:不想连服务器或者没有服务器,想在本地调试服务,该需求就非常重要。基于WSL2安装docker后,…...

376. 摆动序列——【Leetcode每日刷题】
376. 摆动序列 如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为 摆动序列 。第一个差(如果存在的话)可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。 例如, [1, 7, 4, 9, 2, 5] 是一个…...
mgre实验
实验思路 1、首先根据拓扑结构合理分配IP地址,并对各个路由器的IP地址和R5环回接口的IP地址进行配置。 2、让私网中的边界路由器对ISP路由器做缺省路由。 3、根据实验要求,对需要配置不同类型认证的路由器进行认证配置,和需要不同封装的协议…...
)
一文彻底了解Zookeeper(介绍篇)
zookeeper 是什么? zookeeper是一个分布式协作框架,提供高可用,高性能,强一致等特性 zookeeper 有哪些应用场景? 分布式锁:分布式锁是指在分布式环境中,多个进程或线程需要互斥地访问某个共享…...
1. ELK Stack 理论篇之什么是ELK Stack?
ELK Stack 理论篇之什么是ELK Stack?1.1 什么是 ELK Stack?1.2 ELK Stack的发展史1.2.1 Elasticsearch1.2.2 引入 Logstash 和 Kibana,产品更强大1.2.3 社区越来越壮大,用例越来越丰富1.2.4 然后我们向 ELK 中加入了 Beats1.2.5 那么&#x…...
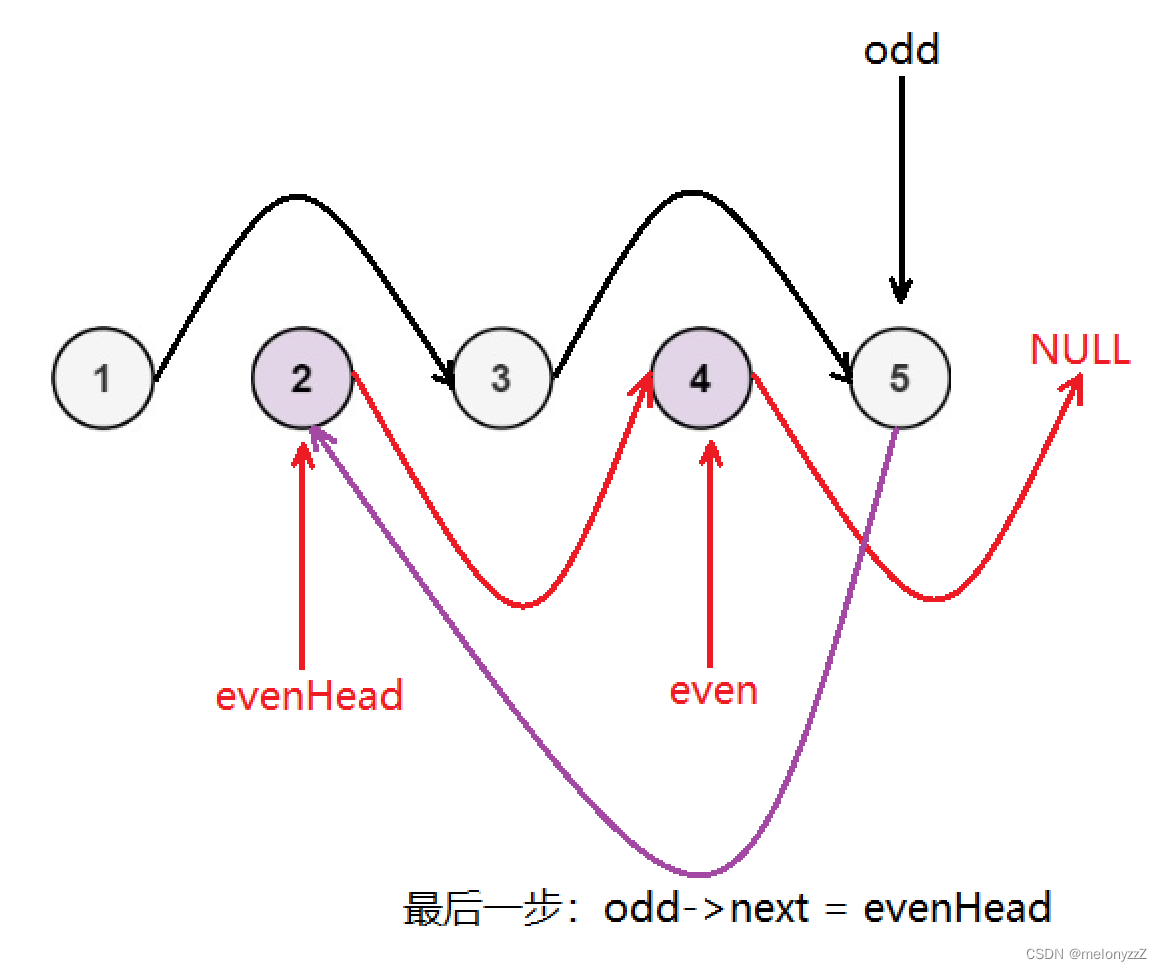
两道有关链表的练习
目录 一、分割链表 二、奇偶链表 一、分割链表 给你一个链表的头节点 head 和一个特定值 x ,请你对链表进行分隔,使得所有 小于 x 的节点都出现在 大于或等于 x 的节点之前。 你不需要 保留 每个分区中各节点的初始相对位置。 示例 1: 输…...
Python uiautomator2安卓自动化测试
一、前言 uiautomator2是Python对Android设备进行UI自动化的库,支持USB和WIFI链接,可以实现获取屏幕上任意一个APP的任意一个控件属性,并对其进行任意操作。 重点是它可以实现安卓自动化采集,甚至是群控采集,且安装和…...

Leetcode. 160相交链表
文章目录指针解法指针解法 核心思路 : 先 分别求两个链表的长度 然后长的链表先走 差距步(长-短) 最后长链表和短链表同时走 ,第一地址相同的就是交点 ,注意一定是地址相同 不可能出现上图这种情况 ,因为C1…...

MDPs —— 马尔可夫决策定义与算法
文章目录MDPs 定义——由实例开始时序决策问题给游戏增点乐子*为什么要有折扣游戏的解——原则所以,什么是 MDPs?MDPs 的基本原理、表示光环原理效用的求解是反向传播的原则不变条件MDPs 的表示MDPs 求解效用迭代法缺点原则迭代法MDPs 定义——由实例开始…...
【C++】图
本文包含了图的基本概念 1.相关概念 1.1 无/有向 无向图:每一个顶点之间的连线没有方向 有向图:连线有方向(类似离散数学的二元关系 <A,B>代表从A到B的边,有方向) <A,B>中A为始点,B为终点在…...

尾递归优化
文章目录1. 前言2. 什么尾调用(Tail Call)?3. 尾调用优化4. Linux内核下的尾递归优化使用5. 参考资料1. 前言 限于作者能力水平,本文可能存在谬误,对此给读者带来的损失,作者不错任何承诺。 2. 什么尾调用…...

P1120 小木棍(搜索+剪枝)
题目链接:P1120 小木棍 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 样例输入: 9 5 2 1 5 2 1 5 2 1 样例输出: 6 分析:这道题一看数据范围就知道是搜索,但关键是需要剪枝。 首先我们求出所有木棍的长度和&am…...
【专项训练】动态规划-3
动态规划:状态转移方程、找重复性和最优子结构 分治 + 记忆化搜索,可以过度到动态规划(动态递推) function DP():# DP状态定义# 需要经验,需把现实问题定义为一个数组,一维、二维、三维……dp =[][] # 二维情况for i = 0...M:...
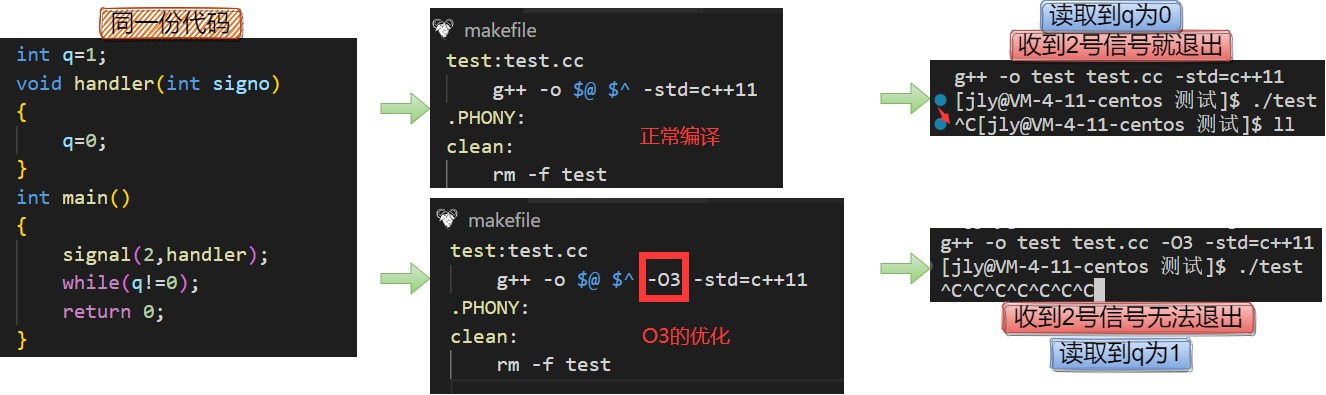
【Linux】信号+再谈进程地址空间
目录 一、Linux中的信号 1、Linux中的信号 2、进程对信号的处理 3、信号的释义 二、信号的捕捉 1、信号的捕捉signal() 2、信号的捕捉sigaction() 三、信号如何产生? 1、kill()用户调用kill向操作系统发送信号 通过命令行参数模仿写一个kill命令 2、rais…...
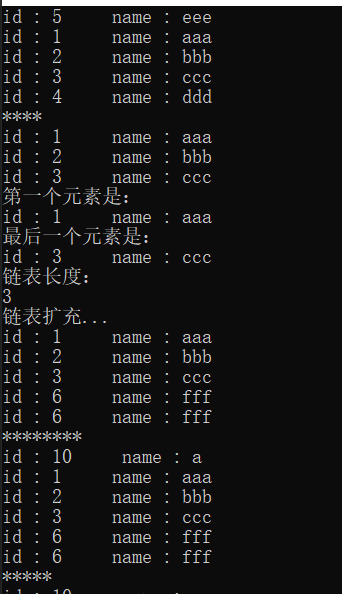
C++回顾(二十一)—— list容器
21.1 list概述 list是一个双向链表容器,可高效地进行插入删除元素。list不可以随机存取元素,所以不支持at.(pos)函数与[]操作符。It(ok) it5(err)需要添加头文件:#include <list> 21.2 list构造 (1)默认构造…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...
