【C++】图
本文包含了图的基本概念
1.相关概念
1.1 无/有向
无向图:每一个顶点之间的连线没有方向
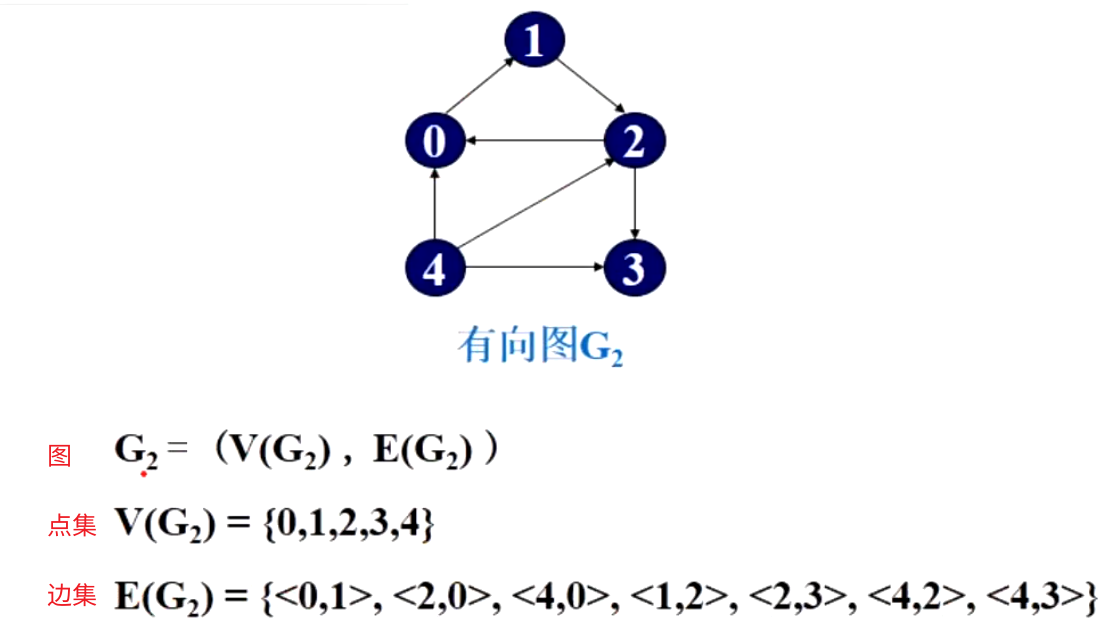
有向图:连线有方向(类似离散数学的二元关系 <A,B>代表从A到B的边,有方向)
<A,B>中A为始点,B为终点
在无向图中,(V,U)和(U,V)是同一条边
1.2 顶点和边
图中的节点叫做顶点。
顶点之间的线条就是边,表示事物与事物之间的关系。
1.3 自回路/多重图

1.4 完全图
图中每一个顶点都有连线(有最多的边数)就叫做完全图
设顶点为N个
- 无向完全图中
n(n-1)/2条边 - 有向完全图中
n(n-1)条边
1.5 邻接与关联
无向图中(u,v)是一条边
- 顶点u和v邻接
- 边
(u,v)与顶点u和v相关联
1.6 子图
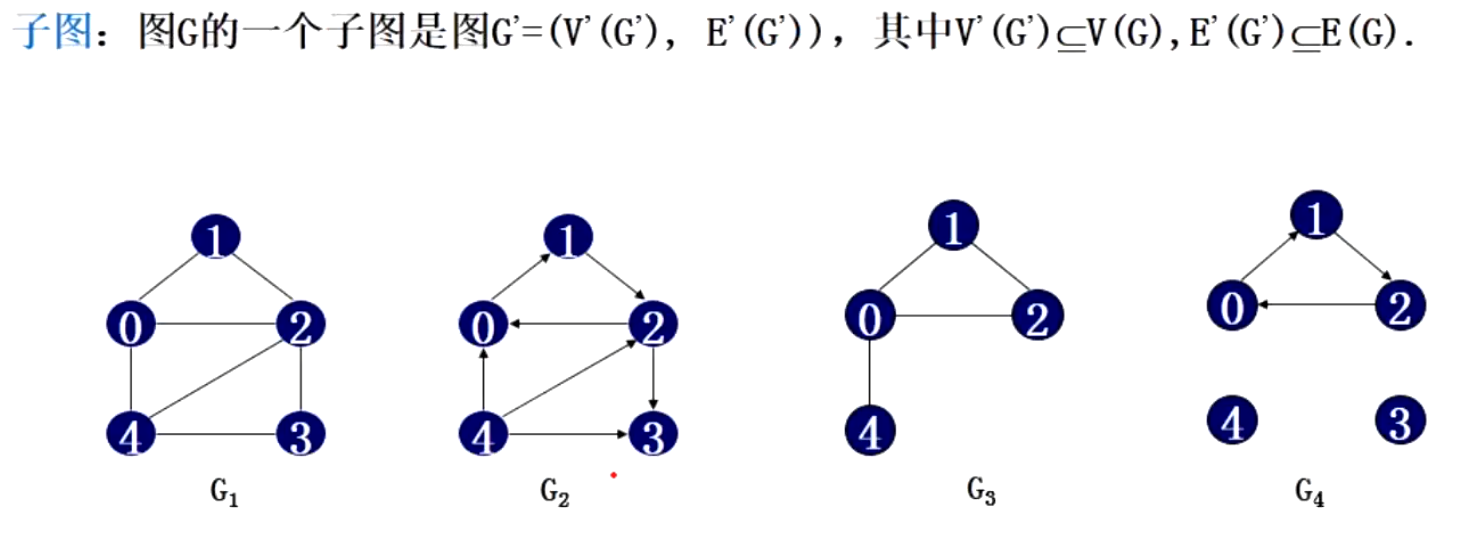
图中G3是G1的子图,G4是G2的子图
简单说来,就是子图是原图的一部分,包括顶点、边(注意方向)都是原图中的一部分
1.6 路径
路径是顶点序列
路径是一个节点到另外一个节点需要经过的边
- 路径长度:路径上边的数目
- 简单路径:除起点、终点可以相同外,路径中其余顶点不相同
- 回路:起点和重点相同的简单路径
1.7 连通图
两个顶点之间只要有路径,那就是连通的
- 连通图:无向图中任意两点之间都有路径,那么就是一个连通图
- 连通分量:无向图的极大连通子图
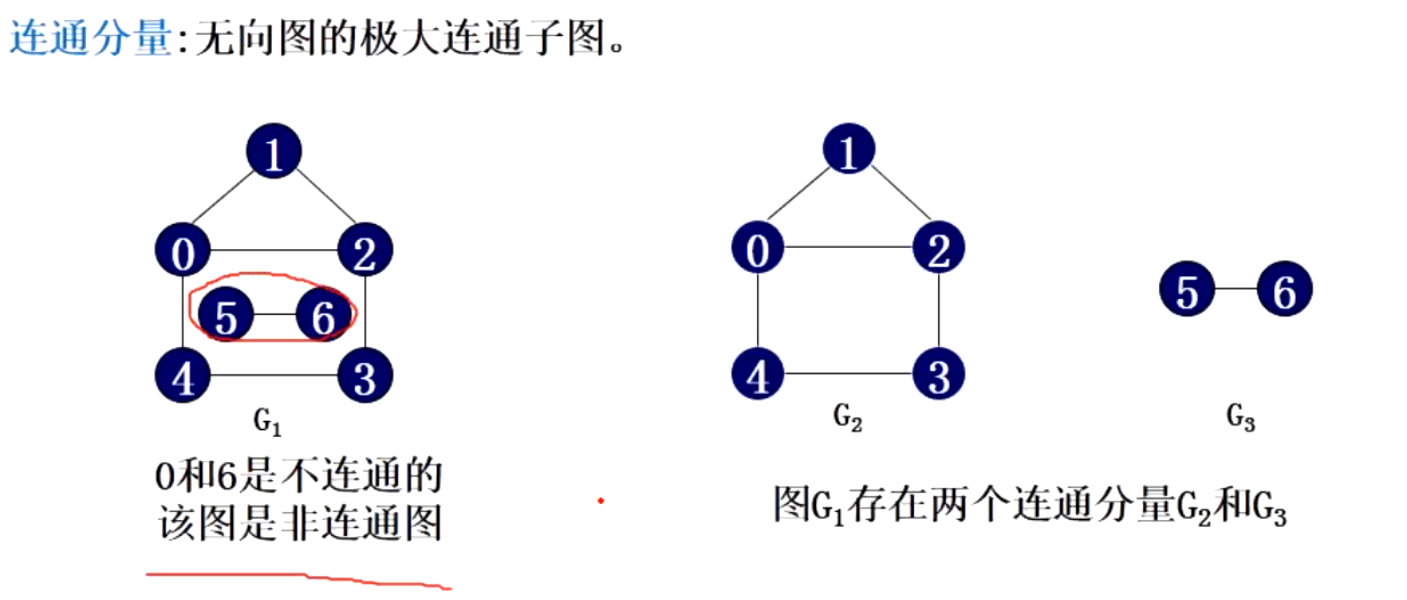
注意,虽然连通分量被称为“极大连通子图”,但它并不是节点最多的哪一个。比如上图中的G2和G3都是极大连通子图。
- 强连通图:有向图中,如果两个顶点之间U和V之间有U到V的路径,那就一定有从V到U的路径
- 强连通分量:有向图的极大联通子图

强连通图G1的极大强连通分量就是它自己(只有非强连通图才有多个强连通分量)
上图中G2就不是强联通图,因为4节点没有入边(也就没有节点能到4)
- 第三图的上半部分并非G1的强连通分量,但是是G2的强力连通分量。
- 同时,单独的4顶点也是一个强连通分量(单独顶点都是)
1.7 顶点的度
度:与该顶点相关联的边的数目
- 入度:射入v的边的数目
- 出度:从v射出去的边的数目
1.8 生成树
生成树包含图中的所有顶点,但是只有足够构成一颗树的n-1条边
- 因为n-1条边再加上一条就会构成回路
- 生成树中不包含回路
1.9 网
给图中的每条边都添加上权值,带权的图称为网
2.表示法
2.1 邻接矩阵
用二维数组来表示每个顶点之间的关系(矩阵)

优缺点
优点
- 便于判断两个顶点之间是否有边,可以直接根据下标判断,
O(1) - 便于计算各个顶点的度
- 无向图:第i行元素之和就是顶点i的度(前提是用1来表示)
- 有向图:第i行元素之和为顶点i的出度;第i列为入度
缺点
- 如果节点多,边少,就会出现空间浪费
- 无法方便地找到一个顶点和那一条边相连(需要遍历)
- 对于无向图,也会出现空间浪费
2.2 邻接表
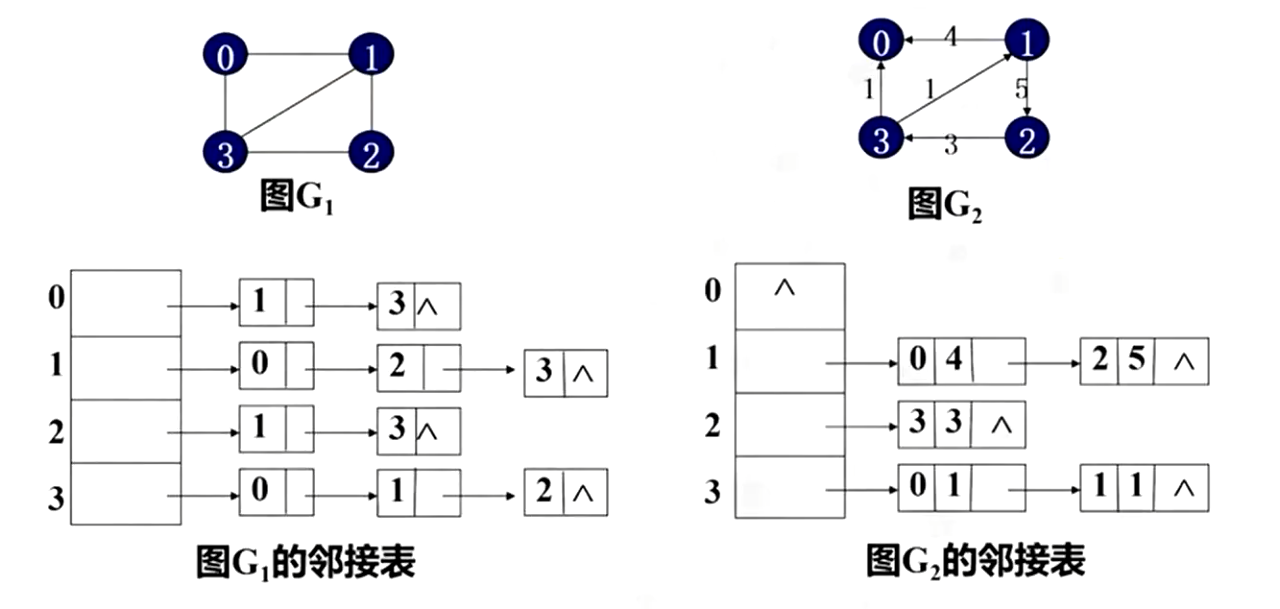
邻接表有些类似于哈希表的拉链法。每一个节点后面跟着一个单链表,用于存储与这个节点相连的节点。
在G2的有向图中,一般存储的是出度表,即从该节点出发的边。如果边有权值,则还需要存储权值
优缺点
优点:
- 可以快速找到一个节点和谁相连(出度)
缺点
- 不便于判断两个顶点之间是否有边
- 不便于计算有向图各个顶点的度(需要遍历所有节点)
关于第二个缺点,可以新增一个入度表(即一个出度表/一个入读表)来计算。但是这样会增加时空复杂度。
3.遍历
3.1 深度优先DFS
深度优先以递归为基本思路,从一个结点开始,递归向后遍历这个节点的单链表中的节点。

为了避免同一个节点遍历多次,我们需要有一个bool数组来标识一个节点是否遍历过。如果遍历过,则把对应下标的值设定为true来标识
由于深度优先的递归部分只能遍历连通图。若出现了上图中非联通的情况,需要我们在外循环中重新遍历一下bool标识数组,确认所有节点都遍历完成。
如果漏了节点(就是没有和其他节点联通的独立节点)那么就以此节点开头再进行一次深度遍历。

3.2 广度优先BFS
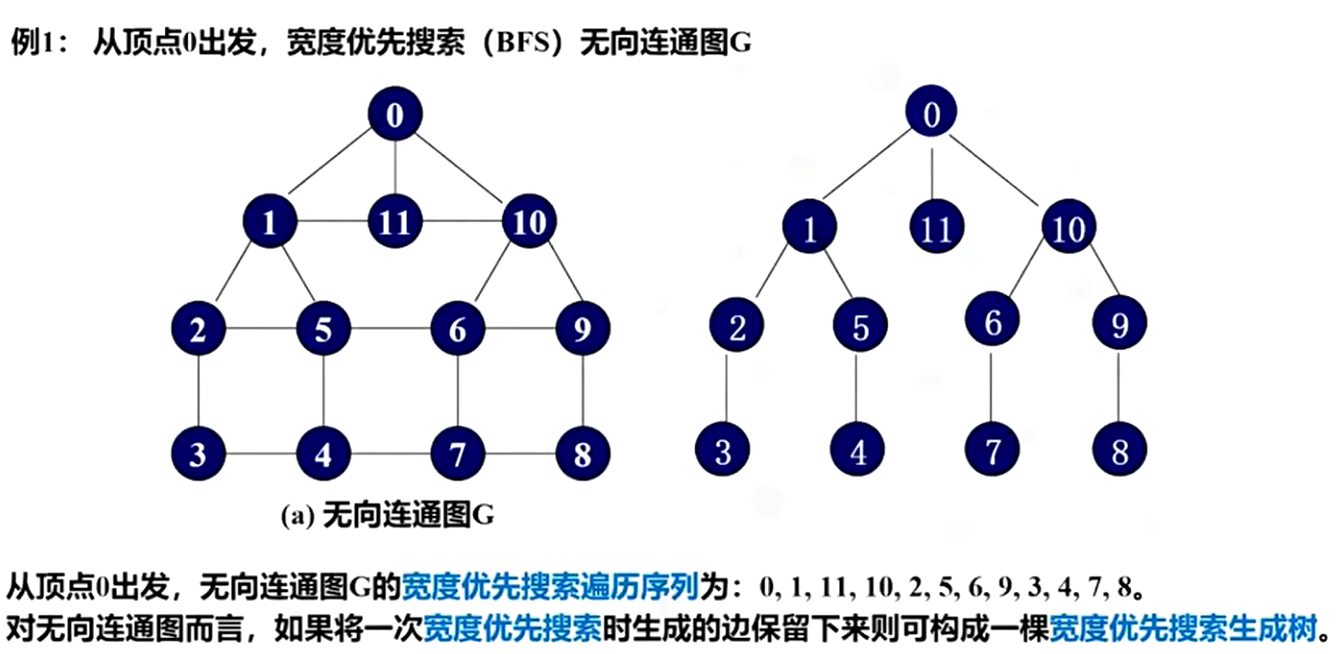
广度优先遍历类似二叉树的层序遍历,依靠循环+队列来完成遍历
- 入起始节点,打印起始节点的值
- 出队头节点(第一次的时候是起始节点)往队列中入该节点单链表中的所有节点
- 依此类推,出一个节点,就入这个节点单链表中的所有节点
- 同样地用一个
bool数组标识节点是否被访问。如果被访问了则跳过该节点 - 也需要在队列循环结束后遍历一遍
bool数组,确认所有节点都访问完毕。

3.3 判断一个图是否连通
使用任何遍历方式,遍历完毕后检查bool数组
若有节点没有被访问,则说明是非连通图
4.拓扑排序
https://blog.csdn.net/qq_43448856/article/details/119959241
给定一个图,每次都选择一个无入度(没有入边)的节点加入序列中,并删除该节点的出边
最终得到的序列就是一个拓扑排序之后的序列
- 每次删除出边后,都可能形成新的无入度的节点
因此,针对同一棵树的拓扑排序序列,可能有多种不同的情况
5.最小生成树算法
生成树的概念参考 1.8 生成树,最小生成树即让生成树中所有边的权值加起来最小
5.1 普里姆Prim

如图中所示,我们先根据这个树的结构构造三个数组
- nearest代表和这个节点最近的节点(默认为-1)
- lowcost代表和这个节点最近节点的权值(默认为无穷大)
- mark是一个bool数组,标识该节点是否已经加入到最小生成树
当我们每从图中取出一个节点的时候,就需要更新这三个表
如图,当我们取走0之后,就需要更新和0连通的三个节点,其中nearest代表刚刚删除掉的节点0,lowcost代表它们和0相连边的权值;同时要把mark中0改为true,表明0已经加入生成树了

第二次选取的时候,遍历lowcost表,找到权值最小的边为(0,2)权值为1。此时就把2加入进去,并更新与2相连的节点3(注,必须要权值更小才需要更新)

依次遍历,直到所有节点都加入了最小生成树(左下角的图)
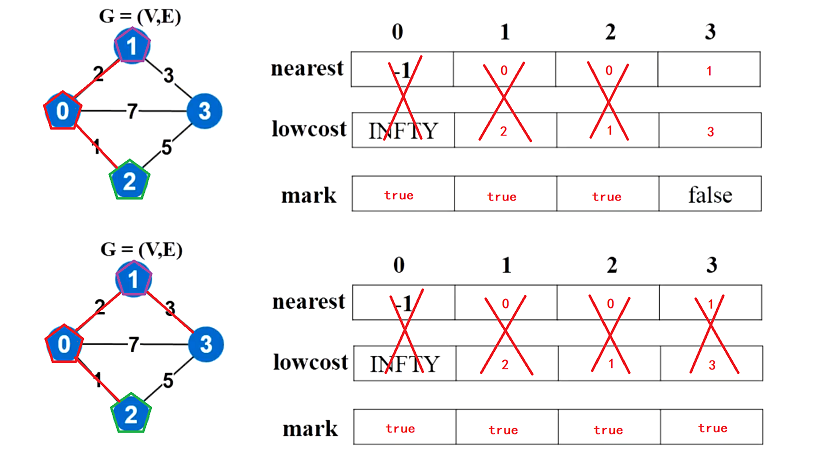
该算法的时间复杂度为O(N^2),只与节点的数量N有关
5.2 克鲁斯卡尔Kruskal

构建一个和原图一样的节点图(无边)在原图中查找权值最小的边,判断其节点是否已经相同,如果没有形成环,则加入到最小生成树的图中
判断是否成环可以通过并查集解决
如下图,先遍历所有边,发现(0,2)的权值最小,判断该边加入后并不会使生成树形成环,则加入该边
- 下图中
(0,2)之间的边1已经移动到了T图上 - 同时将0和2加入到同一个并查集的合集内
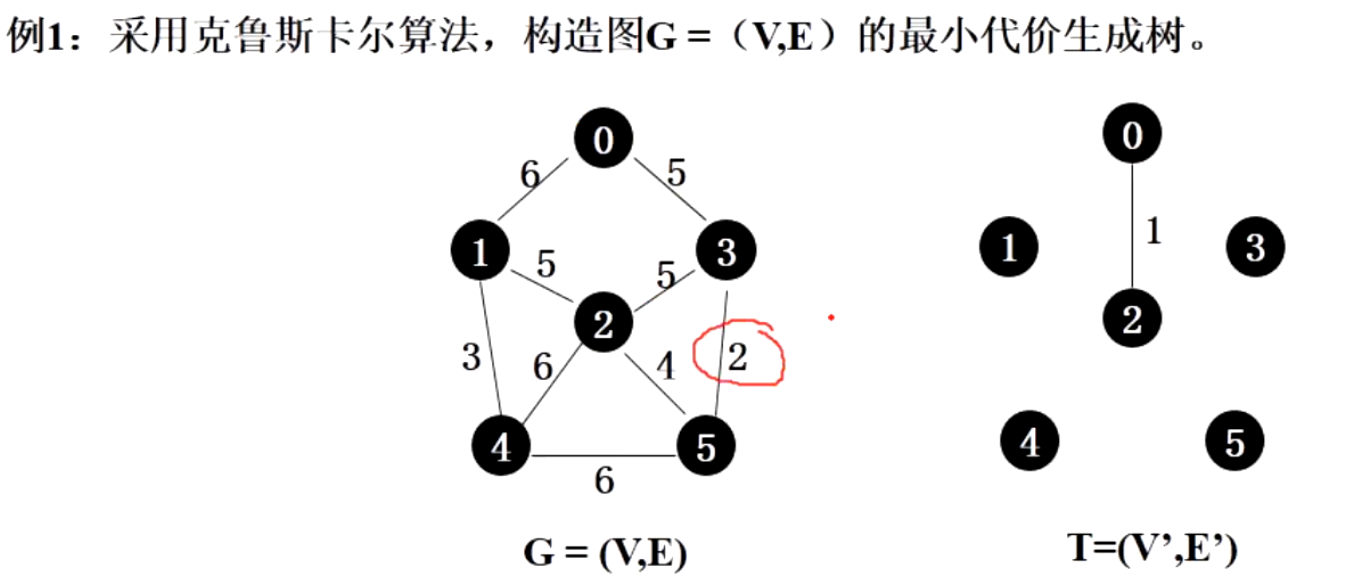
同理继续找权值最小的边,加入到生成树中。如下,将3边移动到右图。

此时我们遇到了3条权值最小的边,权值都为5。此时可以随便加入一条边即可(不能使生成树成环)
如下图中(0,3)和(2,3)的边加入后会使图成环,不能选择该边
- 并查集中0、2、3、5已经在一个集合中,此时判断
(0,3)在一个集合,该边不能加入;(2,3)在一个集合中,该边不能加入
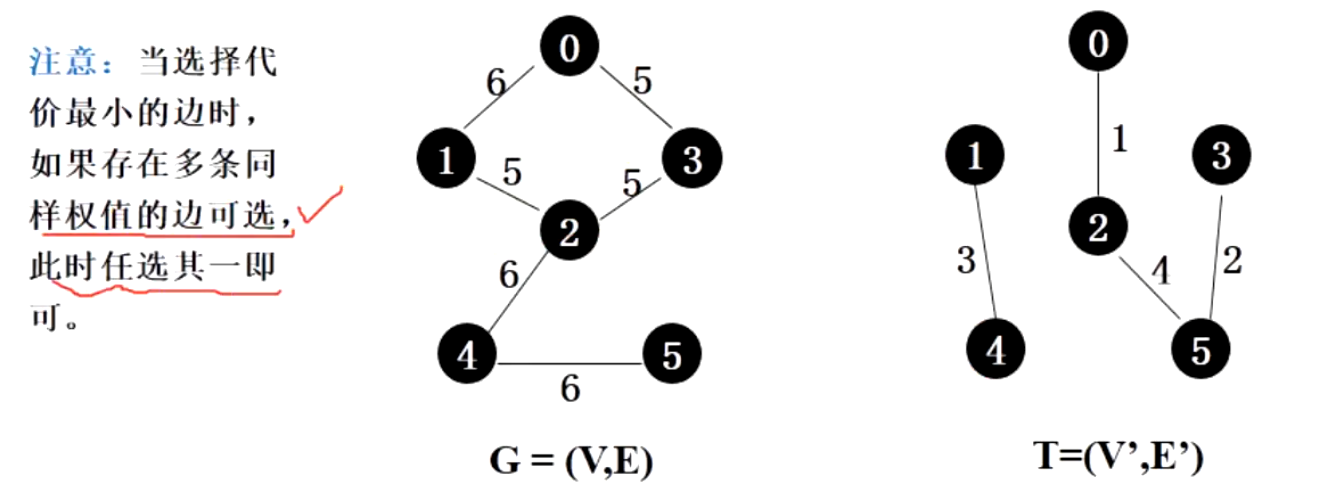
应该选择(1,2)这条边,其不会让树成环

此时所有边都已经连起来了,最小生成树生成成功
算法分析


该算法的时间复杂度为O(E*logE),其中E为边的数目
6.最短路径
带权有向图中,把一条路径(仅考虑简单路径)上所经边的权值之和定义为该路径的路径长度
从源点到终点可能不止一条路径,把路径长度最短的那条路径称为最短路径
6.1 单源最短路径
思路有些类似并查集,path数组中存放的是每一个节点的上一条路径,若下标1处存放0,则代表是从0走到1。同时d数组中标识从0走到下标1的长度。

把1加到s序列之后,发现0到节点2的路径长度缩短了,从原本的(0,2)的6变成了现在(0,1)+(1,2)的4+1=5,长度缩短,对应d数组中下标2处也需要更新
继续下去,直到U数组中没有节点,S数组中节点满,即可获得一个从0出发到任何节点的单源最短路径
6.1.1 狄克斯特拉算法Dijkstra
求解单源最短路径问题的算法
前提:给定一个带权有向图G和源点v,限定各边上的权值大于等于0
基于定理:最短路径上的顶点的最短路径就是该路径
理解:现有一条v到u的最短路径v->……->a->u,那么v到a的最短路径即为v->……->a
算法思路
把图G中的顶点集合V分成两部分:
第一部分,为已求出最短路径的顶点集合(用S表示,初始时S中只有一个源点,以后每求得一条最短路径v,……,u,就将u加入到集合S中,直到全部顶点都加入到S中,算法结束)
第二部分,为其余未求出最短路径的顶点集合(用U表示)
过程:
- 初始化:S只包含源点即S={v},v的最短路径为0。U包含除v以外的其他顶点,U中顶点i距离为边上的权值(若v与i直接相连)或∞(v与i不是直接相连)

- 从U中选取一个距离v最小的顶点u,把u加入S中(该选定的距离就是v到u的最短路径长度)


- 以u为新考虑的中间点,修改U中各顶点i的最短路径长度
若从源点v到顶点 i的最短路径长度(经过顶点u)比原来最短路径长度(不经过顶点u)短,则修改顶点 i的最短路径长度

- 重复2、3步,直至所有顶点都包含在S中
代码设计
着重解决两个问题:
- 如何存放最短路径长度?
用一维数组d[i]存储。源点v默认,d[i]表示源点到顶点i的最短路径长度
如d[2]=12表示源点到顶点2的最短路径长度为12
- 如何存放最短路径?
用一维数组path[]存储。path数组中所存储的数组代表当前顶点在最短路径中的前驱顶点
如path[3]=1,表示在最短路径中,顶点3的前驱顶点是顶点1
算法演示

这是初始化状态
发现数组d中顶点1距离源点距离最近,那么就将顶点1加入到S中

这时,我们需要更新剩余点的最短路径长度和最短路径
显然,顶点2,3,4,5,6并不会都做更新。只有与顶点1直接相连的顶点才有可能会受影响。在上图中会受影响的为顶点2和顶点4

原本顶点2的最短路径长度是6,最短路径是<0,2>。现在由于顶点1的引入,最短路径长度变为5,最短路径变为<0,1>,<1,2>
顶点4同理!
至此,就完成了一次顶点的引入。下面重复上述操作至所有顶点都在S中即可
下面是全过程:
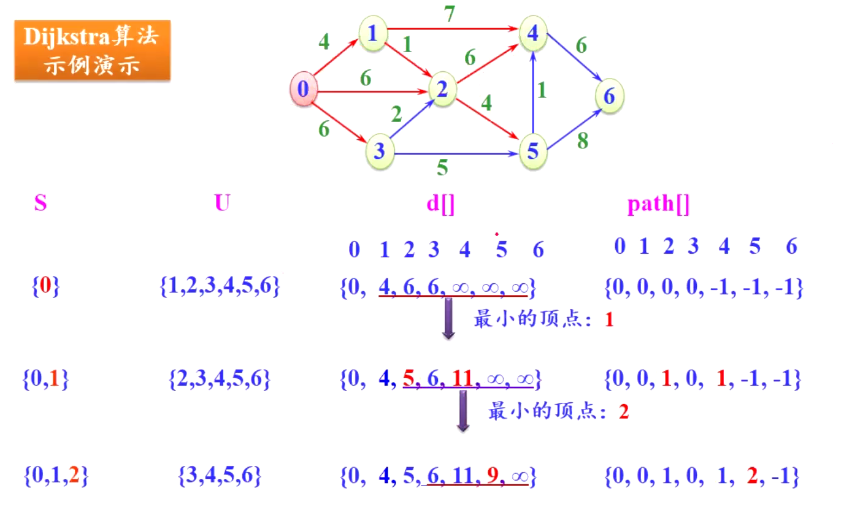
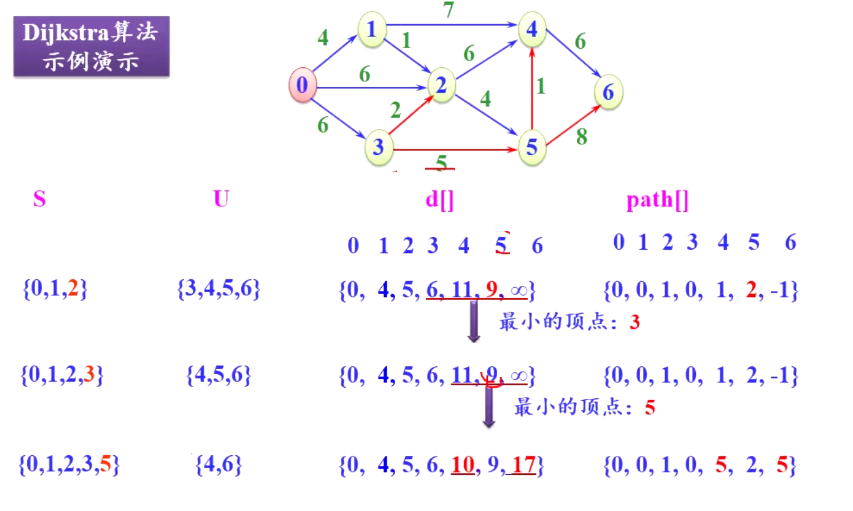

总结一下:在更新d和path数组时,只有与本次引入S中的顶点i直接相连的后驱顶点才有可能发生改变,其余顶点是不可能变的
现在我们利用d和path数组来求解最短路径长度和最短路径:
- 求源点0到终点6的最短路径长度
即为d[6]的值,为16
- 求0到6的最短路径
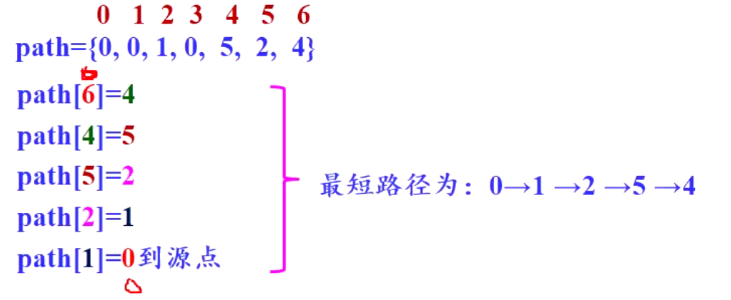
从终点往源点找
时间复杂度
时间复杂度为 O(n2)
相关文章:

【C++】图
本文包含了图的基本概念 1.相关概念 1.1 无/有向 无向图:每一个顶点之间的连线没有方向 有向图:连线有方向(类似离散数学的二元关系 <A,B>代表从A到B的边,有方向) <A,B>中A为始点,B为终点在…...

尾递归优化
文章目录1. 前言2. 什么尾调用(Tail Call)?3. 尾调用优化4. Linux内核下的尾递归优化使用5. 参考资料1. 前言 限于作者能力水平,本文可能存在谬误,对此给读者带来的损失,作者不错任何承诺。 2. 什么尾调用…...

P1120 小木棍(搜索+剪枝)
题目链接:P1120 小木棍 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 样例输入: 9 5 2 1 5 2 1 5 2 1 样例输出: 6 分析:这道题一看数据范围就知道是搜索,但关键是需要剪枝。 首先我们求出所有木棍的长度和&am…...
【专项训练】动态规划-3
动态规划:状态转移方程、找重复性和最优子结构 分治 + 记忆化搜索,可以过度到动态规划(动态递推) function DP():# DP状态定义# 需要经验,需把现实问题定义为一个数组,一维、二维、三维……dp =[][] # 二维情况for i = 0...M:...
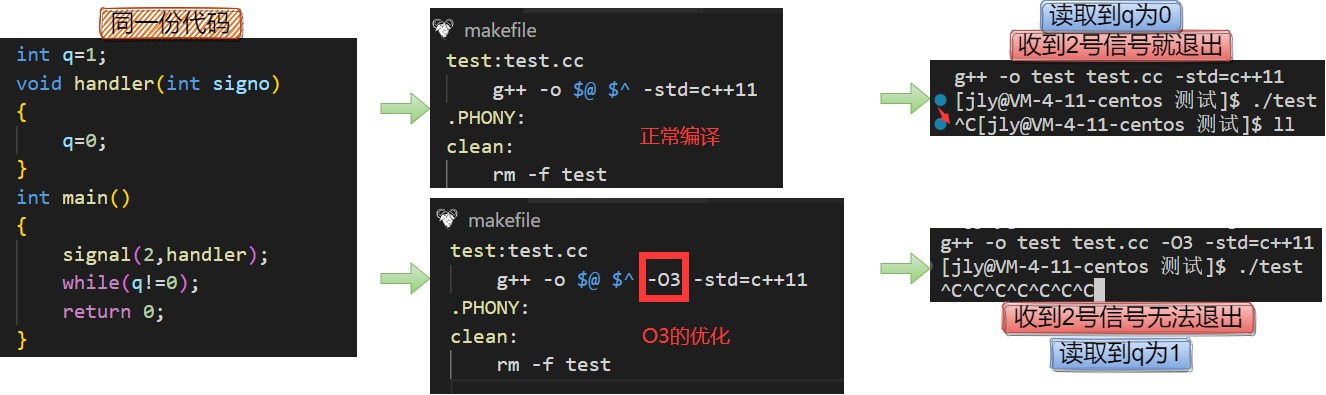
【Linux】信号+再谈进程地址空间
目录 一、Linux中的信号 1、Linux中的信号 2、进程对信号的处理 3、信号的释义 二、信号的捕捉 1、信号的捕捉signal() 2、信号的捕捉sigaction() 三、信号如何产生? 1、kill()用户调用kill向操作系统发送信号 通过命令行参数模仿写一个kill命令 2、rais…...
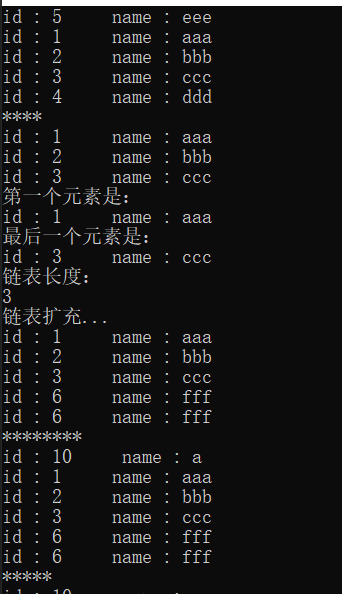
C++回顾(二十一)—— list容器
21.1 list概述 list是一个双向链表容器,可高效地进行插入删除元素。list不可以随机存取元素,所以不支持at.(pos)函数与[]操作符。It(ok) it5(err)需要添加头文件:#include <list> 21.2 list构造 (1)默认构造…...

爱国者一体机电脑蓝屏怎么U盘重装系统教学?
爱国者一体机电脑蓝屏怎么U盘重装系统教学?有用户使用的爱国者一体机电脑开机了之后突然变成了蓝屏的了。而且无法继续使用了,那么遇到这样的蓝屏问题怎么去进行系统的重装呢?一起来看看以下的U盘重装系统教学吧。 准备工作: 1、U…...
)
Vue学习笔记(9)
9.1 axios 9.1.1 概述 Axios是一个流行的基于Promise的HTTP客户端,用于在浏览器和Node中发送HTTP请求。它可以用于处理各种请求类型,例如GET,POST等。Axios可以很容易地与现代前端框架和库集成,例如React,Vue等。 A…...
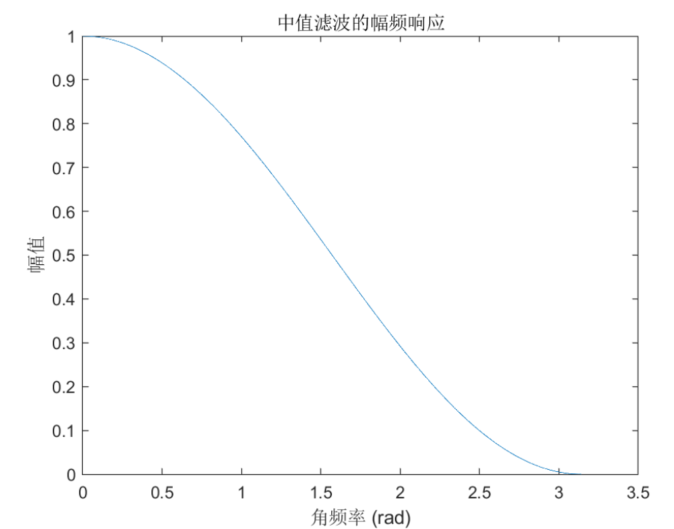
中值滤波+Matlab仿真+频域响应分析
中值滤波 文章目录中值滤波理解中值滤波的过程Matlab 实现实际应用频域分析中值滤波是一种滤波算法,其目的是去除信号中的噪声,而不会对信号本身造成太大的影响。它的原理非常简单:对于一个给定的窗口大小,将窗口内的数值排序&…...

自然语言处理中数据增强(Data Augmentation)技术最全盘点
与“计算机视觉”中使用图像数据增强的标准做法不同,在NLP中,文本数据的增强非常少见。这是因为对图像的琐碎操作(例如将图像旋转几度或将其转换为灰度)不会改变其语义。语义上不变的转换的存在是使增强成为Computer Vision研究中…...
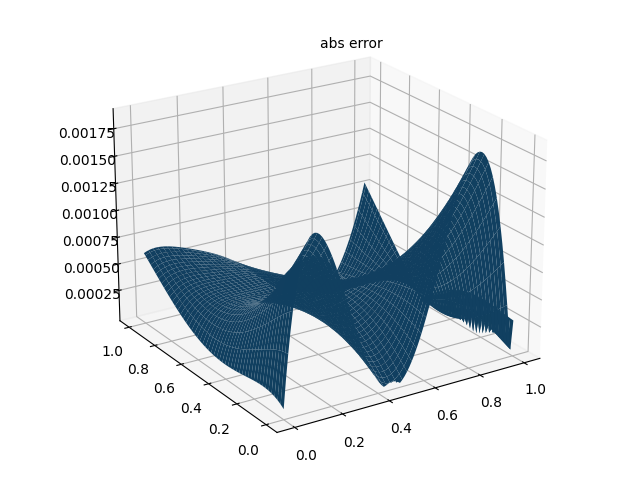
PINN解偏微分方程实例1
PINN解偏微分方程实例11. PINN简介2. 偏微分方程实例3. 基于pytorch实现代码4. 数值解参考资料1. PINN简介 PINN是一种利用神经网络求解偏微分方程的方法,其计算流程图如下图所示,这里以偏微分方程(1)为例。 ∂u∂tu∂u∂xv∂2u∂x2\begin{align} \frac{…...

【python 基础篇 十二】python的函数-------函数生成器
目录1.生成器基本概念2.生成器的创建方式3.生成器的输出方式4.send()方法5.关闭生成器6.注意事项1.生成器基本概念 是一个特色的迭代器(迭代器的抽象层级更高)所以拥有迭代器的特性 惰性计算数据 节省内存 ----就是不是立马生成所有数据,而是…...
elasticsearch全解 (待续)
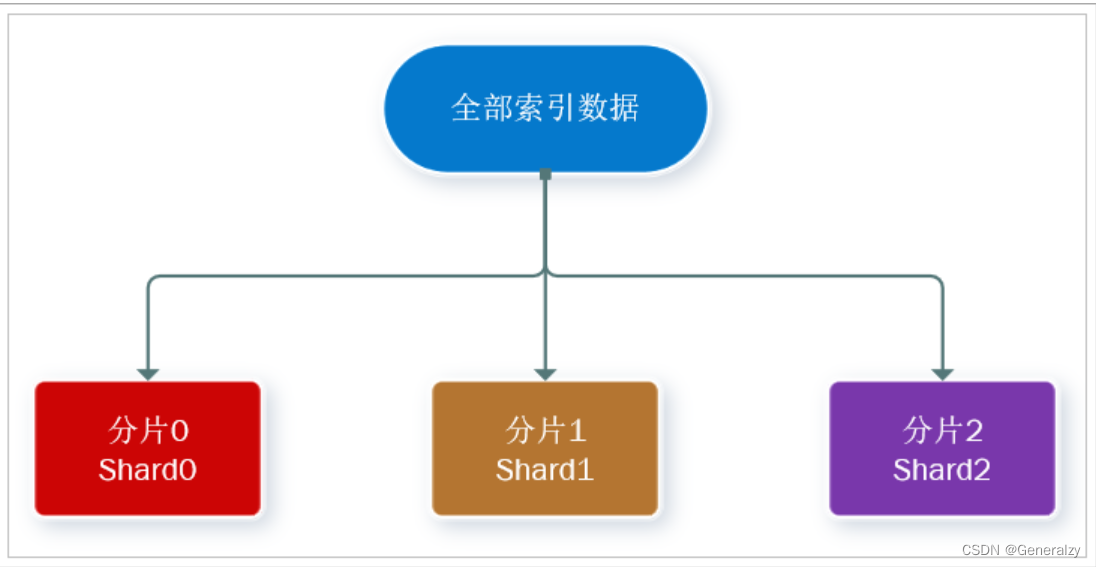
目录elasticsearchELK技术栈Lucene与Elasticsearch关系为什么不是其他搜索技术?Elasticsearch核心概念Cluster:集群Node:节点Shard:分片Replia:副本全文检索倒排索引正向和倒排es的一些概念文档和字段索引和映射mysql与…...

springboot2集成knife4j
springboot2集成knife4j springboot2集成knife4j 环境说明集成knife4j 第一步:引入依赖第二步:编写配置类第三步:测试一下 第一小步:编写controller第二小步:启动项目,访问api文档 相关资料 环境说明 …...

Qt 性能优化:CPU占有率高的现象和解决办法
一、前言 在最近的项目中,发现执行 Qt 程序时,有些情况下的 CPU 占用率奇高,最高高达 100%。项目跑在嵌入式板子上,最开始使用 EGLFS 插件,但是由于板子没有单独的鼠标层,导致鼠标移动起来卡顿,…...

MySQL专题(学会就毕业)
MySQL专题0.准备sql设计一张员工信息表,要求如下:编号(纯数字)员工工号 (字符串类型,长度不超过10位)员工姓名(字符串类型,长度不超过10位)性别(男/女,存储一…...

Java高级技术:单元测试、反射、注解
目录 单元测试 单元测试概述 单元测试快速入门 单元测试常用注解 反射 反射概述 反射获取类对象 反射获取构造器对象 反射获取成员变量对象 反射获取方法对象 反射的作用-绕过编译阶段为集合添加数据 反射的作用-通用框架的底层原理 注解 注解概述 自定义注解 …...

C语言初识
#include <stdio.h>//这种写法是过时的写法 void main() {}//int是整型的意思 //main前面的int表示main函数调用后返回一个整型值 int main() {return 0; }int main() { //主函数--程序的入口--main函数有且仅有一个//在这里完成任务//在屏幕伤输出hello world//函数-pri…...

Cadence Allegro 导出Etch Length by Layer Report报告详解
⏪《上一篇》 🏡《上级目录》 ⏩《下一篇》 目录 1,概述2,Etch Length by Layer Report作用3,Etch Length by Layer Report示例4,Etch Length by Layer Report导出方法4.2,方法14.2,方法2B站关注“硬小二”浏览更多演示视频...
无监督对比学习(CL)最新必读经典论文整理分享
对比自监督学习技术是一种很有前途的方法,它通过学习对使两种事物相似或不同的东西进行编码来构建表示。Contrastive learning有很多文章介绍,区别于生成式的自监督方法,如AutoEncoder通过重建输入信号获取中间表示,Contrastive M…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...

深度剖析 DeepSeek 开源模型部署与应用:策略、权衡与未来走向
在人工智能技术呈指数级发展的当下,大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性,吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型,成为释放其巨大潜力的关键所在&…...
)
LLaMA-Factory 微调 Qwen2-VL 进行人脸情感识别(二)
在上一篇文章中,我们详细介绍了如何使用LLaMA-Factory框架对Qwen2-VL大模型进行微调,以实现人脸情感识别的功能。本篇文章将聚焦于微调完成后,如何调用这个模型进行人脸情感识别的具体代码实现,包括详细的步骤和注释。 模型调用步骤 环境准备:确保安装了必要的Python库。…...

五子棋测试用例
一.项目背景 1.1 项目简介 传统棋类文化的推广 五子棋是一种古老的棋类游戏,有着深厚的文化底蕴。通过将五子棋制作成网页游戏,可以让更多的人了解和接触到这一传统棋类文化。无论是国内还是国外的玩家,都可以通过网页五子棋感受到东方棋类…...
