376. 摆动序列——【Leetcode每日刷题】
376. 摆动序列
如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为 摆动序列 。第一个差(如果存在的话)可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。
-
例如, [1, 7, 4, 9, 2, 5] 是一个 摆动序列 ,因为差值 (6, -3, 5, -7, 3) 是正负交替出现的。
-
相反,[1, 4, 7, 2, 5] 和 [1, 7, 4, 5, 5] 不是摆动序列,第一个序列是因为它的前两个差值都是正数,第二个序列是因为它的最后一个差值为零。
子序列 可以通过从原始序列中删除一些(也可以不删除)元素来获得,剩下的元素保持其原始顺序。
给你一个整数数组 nums ,返回 nums 中作为 摆动序列 的 最长子序列的长度 。
示例 1:
输入:nums = [1,7,4,9,2,5]
输出:6
解释:整个序列均为摆动序列,各元素之间的差值为 (6, -3, 5, -7, 3) 。
示例 2:
输入:nums = [1,17,5,10,13,15,10,5,16,8]
输出:7
解释:这个序列包含几个长度为 7 摆动序列。
其中一个是 [1, 17, 10, 13, 10, 16, 8] ,各元素之间的差值为 (16, -7, 3, -3, 6, -8) 。
示例 3:
输入:nums = [1,2,3,4,5,6,7,8,9]
输出:2
提示:
- 1 <= nums.length <= 1000
- 0 <= nums[i] <= 1000
进阶:你能否用 O(n) 时间复杂度完成此题?
思路:
法一:动态规划
本题大家都很容易想到用动态规划来求解,求解的过程类似最长上升子序列。
- 不过是需要判断两个序列;
- 且需要nums相同长度的数组dp, flg,分别存放记录包括nums[i]在内的最长摆动序列及记录nums[j]与上一个数的差值符号。
法二:贪心
维护峰顶最大,峰谷最小:
- 设立一个 flg 记录前一次 序列摆动的趋势,趋势相反,序列长度 加 1;
- 如果相等元素跳过;
- 如果一直递增,序列长度不变,最后一个值一直更新当前最大值;(这样才有更多的机会遇到较小的值)
- 如果一直递减,序列长度不变,最后一个值一直更新当前最小值。(这样才有更多的机会遇到较大的值)
代码:(Java)
法一:动态规划
import java.util.Arrays;public class WiggleMaxLength {public static void main(String[] args) {// TODO Auto-generated method stubint[] nums = {1,17,5,10,13,15,10,5,16,8};System.out.println(wiggleMaxLength(nums));}public static int wiggleMaxLength(int[] nums) {int n = nums.length;int[] dp = new int[n];//记录包括nums[i]在内的最长摆动序列int[] flg = new int[n];//记录nums[i]与上一个数的差值符号Arrays.fill(dp, 1);Arrays.fill(flg, 0); // 1表示和上一个数的差为正数,-1 表示和上一个数之差为负数 ,0表示相等for(int i = 1; i < n; i++) {for(int j = 0; j < i; j++) {if(nums[i] != nums[j] && flg[j] != (nums[i] > nums[j] ? 1 : -1) && dp[j] + 1 > dp[i]){flg[i] = nums[i] > nums[j] ? 1 : -1;dp[i] = dp[j] + 1;}}}return dp[n - 1];}
}
法二:贪心
public class WiggleMaxLength {public static void main(String[] args) {// TODO Auto-generated method stubint[] nums = {1,17,5,10,13,15,10,5,16,8};System.out.println(wiggleMaxLength(nums));}public static int wiggleMaxLength(int[] nums) {int n = nums.length;int flg = 0;//记录nums[i]与上一个数的差值符号int len = 1;for(int i = 1; i < n; i++) {if(nums[i] == nums[len - 1]) {continue;}else if(flg != (nums[i] > nums[len - 1] ? 1 : -1)){flg = nums[i] > nums[len - 1] ? 1 : -1;nums[len] = nums[i];len++;}else {nums[len - 1] = nums[i];}}return len;}
}
运行结果:

复杂度分析
法一:动态规划
- 时间复杂度:O(n2)O(n^2)O(n2),其中 n 是序列的长度。我们需要两重 for 循环。
- 空间复杂度:O(n)O(n)O(n)。我们需要nums相同长度的数组dp, flg,分别存放记录包括nums[i]在内的最长摆动序列及记录nums[j]与上一个数的差值符号。
法二:贪心
- 时间复杂度:O(n)O(n)O(n),其中 n 是序列的长度。我们只需要遍历该序列一次。
- 空间复杂度:O(1)O(1)O(1)。我们只需要常数空间来存放若干变量。
类似题解题目:
646. 最长数对链
300. 最长递增子序列
注:仅供学习参考!
题目来源:力扣。
相关文章:

376. 摆动序列——【Leetcode每日刷题】
376. 摆动序列 如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为 摆动序列 。第一个差(如果存在的话)可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。 例如, [1, 7, 4, 9, 2, 5] 是一个…...
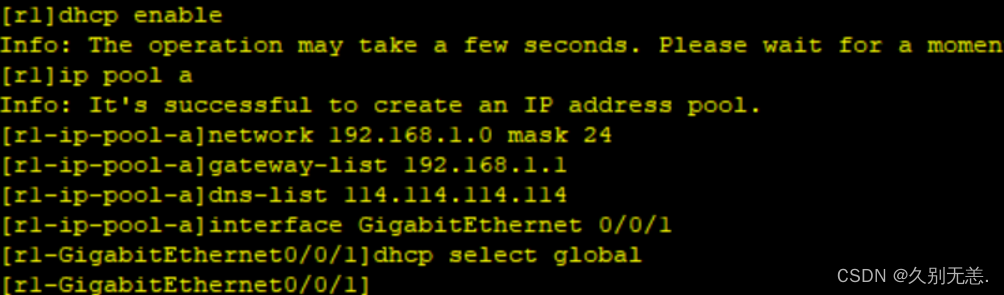
mgre实验
实验思路 1、首先根据拓扑结构合理分配IP地址,并对各个路由器的IP地址和R5环回接口的IP地址进行配置。 2、让私网中的边界路由器对ISP路由器做缺省路由。 3、根据实验要求,对需要配置不同类型认证的路由器进行认证配置,和需要不同封装的协议…...
)
一文彻底了解Zookeeper(介绍篇)
zookeeper 是什么? zookeeper是一个分布式协作框架,提供高可用,高性能,强一致等特性 zookeeper 有哪些应用场景? 分布式锁:分布式锁是指在分布式环境中,多个进程或线程需要互斥地访问某个共享…...
1. ELK Stack 理论篇之什么是ELK Stack?
ELK Stack 理论篇之什么是ELK Stack?1.1 什么是 ELK Stack?1.2 ELK Stack的发展史1.2.1 Elasticsearch1.2.2 引入 Logstash 和 Kibana,产品更强大1.2.3 社区越来越壮大,用例越来越丰富1.2.4 然后我们向 ELK 中加入了 Beats1.2.5 那么&#x…...
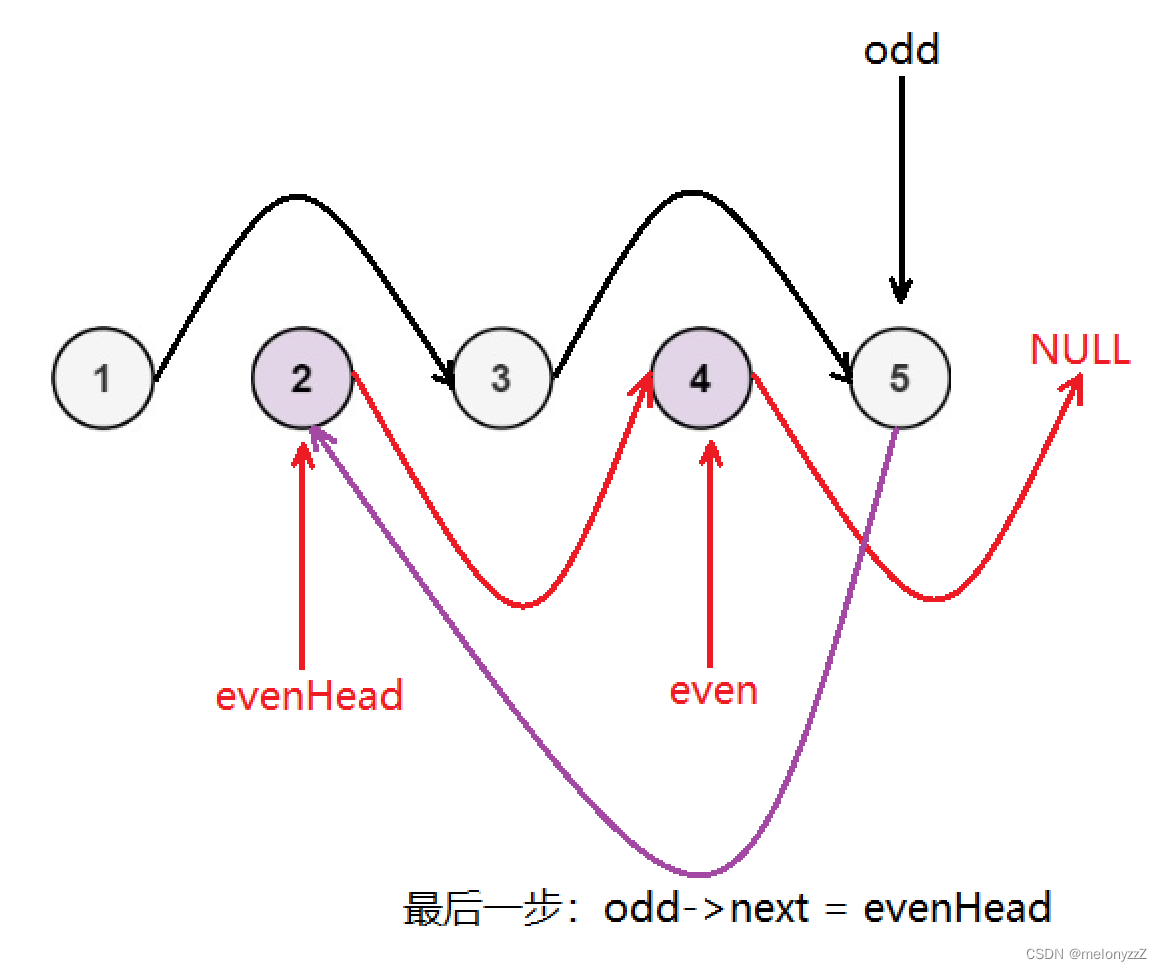
两道有关链表的练习
目录 一、分割链表 二、奇偶链表 一、分割链表 给你一个链表的头节点 head 和一个特定值 x ,请你对链表进行分隔,使得所有 小于 x 的节点都出现在 大于或等于 x 的节点之前。 你不需要 保留 每个分区中各节点的初始相对位置。 示例 1: 输…...
Python uiautomator2安卓自动化测试
一、前言 uiautomator2是Python对Android设备进行UI自动化的库,支持USB和WIFI链接,可以实现获取屏幕上任意一个APP的任意一个控件属性,并对其进行任意操作。 重点是它可以实现安卓自动化采集,甚至是群控采集,且安装和…...

Leetcode. 160相交链表
文章目录指针解法指针解法 核心思路 : 先 分别求两个链表的长度 然后长的链表先走 差距步(长-短) 最后长链表和短链表同时走 ,第一地址相同的就是交点 ,注意一定是地址相同 不可能出现上图这种情况 ,因为C1…...

MDPs —— 马尔可夫决策定义与算法
文章目录MDPs 定义——由实例开始时序决策问题给游戏增点乐子*为什么要有折扣游戏的解——原则所以,什么是 MDPs?MDPs 的基本原理、表示光环原理效用的求解是反向传播的原则不变条件MDPs 的表示MDPs 求解效用迭代法缺点原则迭代法MDPs 定义——由实例开始…...
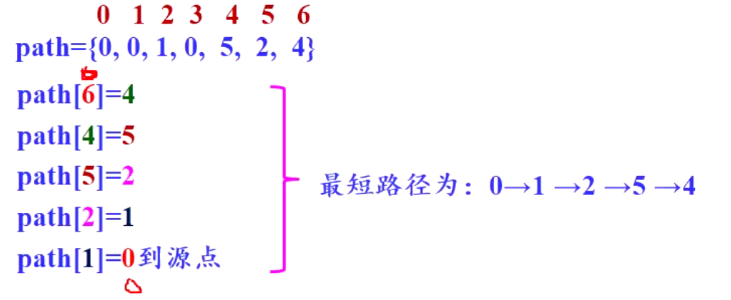
【C++】图
本文包含了图的基本概念 1.相关概念 1.1 无/有向 无向图:每一个顶点之间的连线没有方向 有向图:连线有方向(类似离散数学的二元关系 <A,B>代表从A到B的边,有方向) <A,B>中A为始点,B为终点在…...

尾递归优化
文章目录1. 前言2. 什么尾调用(Tail Call)?3. 尾调用优化4. Linux内核下的尾递归优化使用5. 参考资料1. 前言 限于作者能力水平,本文可能存在谬误,对此给读者带来的损失,作者不错任何承诺。 2. 什么尾调用…...

P1120 小木棍(搜索+剪枝)
题目链接:P1120 小木棍 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 样例输入: 9 5 2 1 5 2 1 5 2 1 样例输出: 6 分析:这道题一看数据范围就知道是搜索,但关键是需要剪枝。 首先我们求出所有木棍的长度和&am…...
【专项训练】动态规划-3
动态规划:状态转移方程、找重复性和最优子结构 分治 + 记忆化搜索,可以过度到动态规划(动态递推) function DP():# DP状态定义# 需要经验,需把现实问题定义为一个数组,一维、二维、三维……dp =[][] # 二维情况for i = 0...M:...
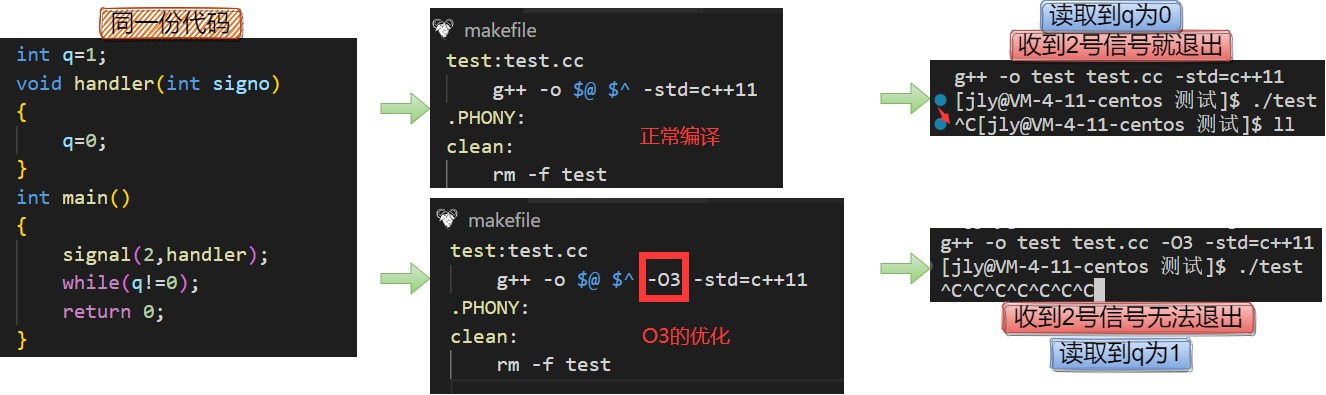
【Linux】信号+再谈进程地址空间
目录 一、Linux中的信号 1、Linux中的信号 2、进程对信号的处理 3、信号的释义 二、信号的捕捉 1、信号的捕捉signal() 2、信号的捕捉sigaction() 三、信号如何产生? 1、kill()用户调用kill向操作系统发送信号 通过命令行参数模仿写一个kill命令 2、rais…...
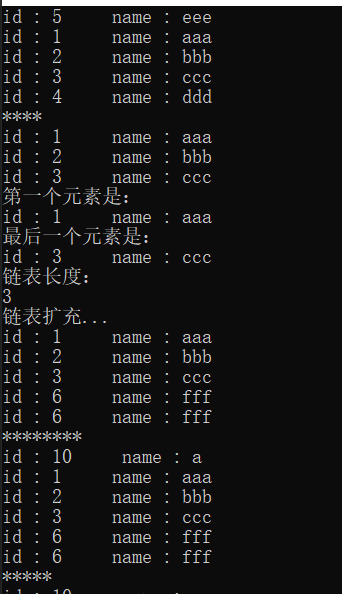
C++回顾(二十一)—— list容器
21.1 list概述 list是一个双向链表容器,可高效地进行插入删除元素。list不可以随机存取元素,所以不支持at.(pos)函数与[]操作符。It(ok) it5(err)需要添加头文件:#include <list> 21.2 list构造 (1)默认构造…...

爱国者一体机电脑蓝屏怎么U盘重装系统教学?
爱国者一体机电脑蓝屏怎么U盘重装系统教学?有用户使用的爱国者一体机电脑开机了之后突然变成了蓝屏的了。而且无法继续使用了,那么遇到这样的蓝屏问题怎么去进行系统的重装呢?一起来看看以下的U盘重装系统教学吧。 准备工作: 1、U…...
)
Vue学习笔记(9)
9.1 axios 9.1.1 概述 Axios是一个流行的基于Promise的HTTP客户端,用于在浏览器和Node中发送HTTP请求。它可以用于处理各种请求类型,例如GET,POST等。Axios可以很容易地与现代前端框架和库集成,例如React,Vue等。 A…...
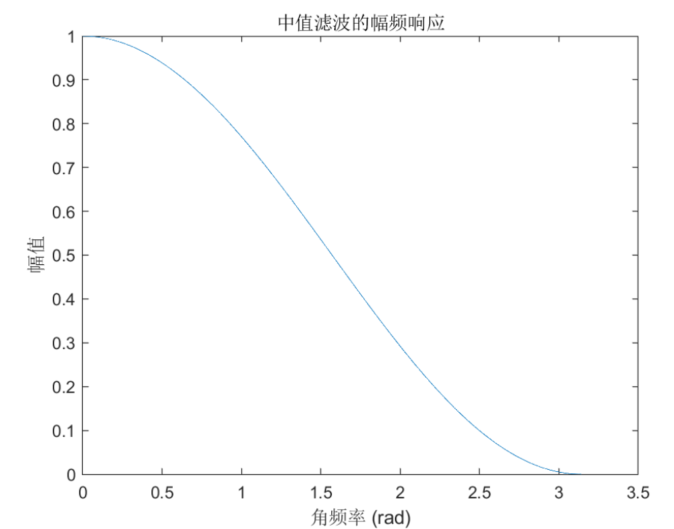
中值滤波+Matlab仿真+频域响应分析
中值滤波 文章目录中值滤波理解中值滤波的过程Matlab 实现实际应用频域分析中值滤波是一种滤波算法,其目的是去除信号中的噪声,而不会对信号本身造成太大的影响。它的原理非常简单:对于一个给定的窗口大小,将窗口内的数值排序&…...

自然语言处理中数据增强(Data Augmentation)技术最全盘点
与“计算机视觉”中使用图像数据增强的标准做法不同,在NLP中,文本数据的增强非常少见。这是因为对图像的琐碎操作(例如将图像旋转几度或将其转换为灰度)不会改变其语义。语义上不变的转换的存在是使增强成为Computer Vision研究中…...
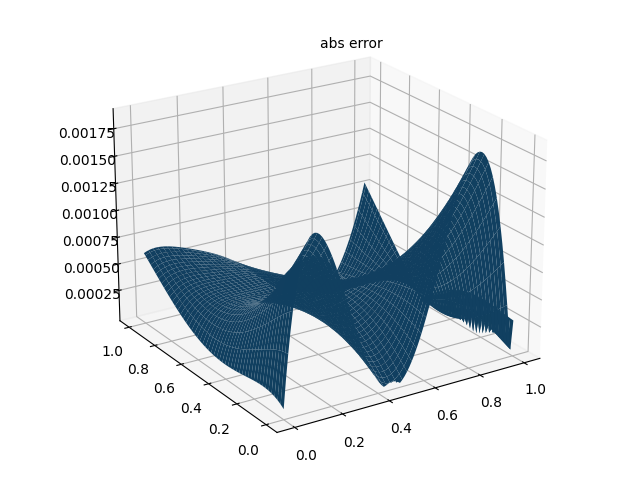
PINN解偏微分方程实例1
PINN解偏微分方程实例11. PINN简介2. 偏微分方程实例3. 基于pytorch实现代码4. 数值解参考资料1. PINN简介 PINN是一种利用神经网络求解偏微分方程的方法,其计算流程图如下图所示,这里以偏微分方程(1)为例。 ∂u∂tu∂u∂xv∂2u∂x2\begin{align} \frac{…...

【python 基础篇 十二】python的函数-------函数生成器
目录1.生成器基本概念2.生成器的创建方式3.生成器的输出方式4.send()方法5.关闭生成器6.注意事项1.生成器基本概念 是一个特色的迭代器(迭代器的抽象层级更高)所以拥有迭代器的特性 惰性计算数据 节省内存 ----就是不是立马生成所有数据,而是…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...
