扩散模型在机器学习中的应用及原理
扩散模型在机器学习中的应用及原理
大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!
什么是扩散模型?
在机器学习中,扩散模型(Diffusion Model)是一种基于随机过程的数学模型,用于描述信息、热量、物质或其他实体在空间中传播和扩散的过程。扩散模型广泛应用于多个领域,如物理学、生物学、经济学以及计算机科学中的机器学习和数据挖掘。
扩散模型在机器学习中的应用
在机器学习领域,扩散模型主要用于以下几个方面:
-
信息传播模型:模拟信息在社交网络中的传播过程,预测信息扩散的路径和影响力。
-
图像处理和分割:通过扩散模型进行图像分割和边缘检测,例如基于扩散过程的分水岭算法。
-
自然语言处理:利用扩散模型分析文本数据中的信息传播和主题演化,如在文本分类和主题建模中的应用。
扩散模型原理
扩散模型基于偏微分方程描述,通常使用的是扩散方程(Diffusion Equation),如下所示:
[ \frac{\partial u}{\partial t} = D \nabla^2 u ]
其中,( u ) 是扩散物质的浓度或信息量,( t ) 是时间,( D ) 是扩散系数,( \nabla^2 ) 是拉普拉斯算子。这个方程描述了物质或信息在空间中扩散的速度和方向。
Java代码示例
以下是一个简单的Java代码示例,演示如何使用扩散模型来模拟信息传播过程:
package cn.juwatech.machinelearning.diffusion;import cn.juwatech.*;public class DiffusionModel {public static void main(String[] args) {// 初始化扩散模型参数double[][] grid = new double[100][100]; // 网格double diffusionRate = 0.2; // 扩散率int timeSteps = 100; // 时间步长// 执行扩散模拟simulateDiffusion(grid, diffusionRate, timeSteps);// 打印结果或进一步处理System.out.println("扩散模拟完成!");}public static void simulateDiffusion(double[][] grid, double diffusionRate, int timeSteps) {int rows = grid.length;int cols = grid[0].length;// 模拟扩散过程for (int t = 0; t < timeSteps; t++) {double[][] newGrid = new double[rows][cols];for (int i = 0; i < rows; i++) {for (int j = 0; j < cols; j++) {double diffusion = diffusionRate * (getNeighborAverage(grid, i, j) - grid[i][j]);newGrid[i][j] = grid[i][j] + diffusion;}}grid = newGrid; // 更新网格状态}}public static double getNeighborAverage(double[][] grid, int x, int y) {// 计算周围邻居节点的平均值// 实现省略,具体实现根据具体问题和数据结构定义return 0.0;}
}
在上述示例中,我们使用Java模拟了一个简单的扩散模型,演示了如何在程序中应用扩散模型来模拟信息传播或物质扩散的过程。
总结
通过本文,您了解了扩散模型在机器学习中的应用及其基本原理。扩散模型作为一种描述信息传播和物质扩散过程的数学工具,在多个领域都有广泛的应用,能够帮助我们理解和预测复杂系统中的动态行为。
相关文章:

扩散模型在机器学习中的应用及原理
扩散模型在机器学习中的应用及原理 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿! 什么是扩散模型? 在机器学习中,扩散模型ÿ…...

fastapi自定义中间件
fastapi自定义中间件 1、自定义中间件类 from fastapi import Request from starlette.middleware.base import BaseHTTPMiddlewareclass MyMiddleware(BaseHTTPMiddleware):def __init__(self, app,*args, **kwargs):super().__init__(app,*args, **kwargs)async def dispat…...

基于 MCU 的开发,能不能对代码进行单元测试?
在基于微控制器(MCU)的开发中,确实可以对代码进行单元测试,并且随着嵌入式软件开发实践的发展,越来越多的团队开始重视并实施单元测试和自动化测试。 单元测试是一种软件测试方法,用于验证程序模块…...
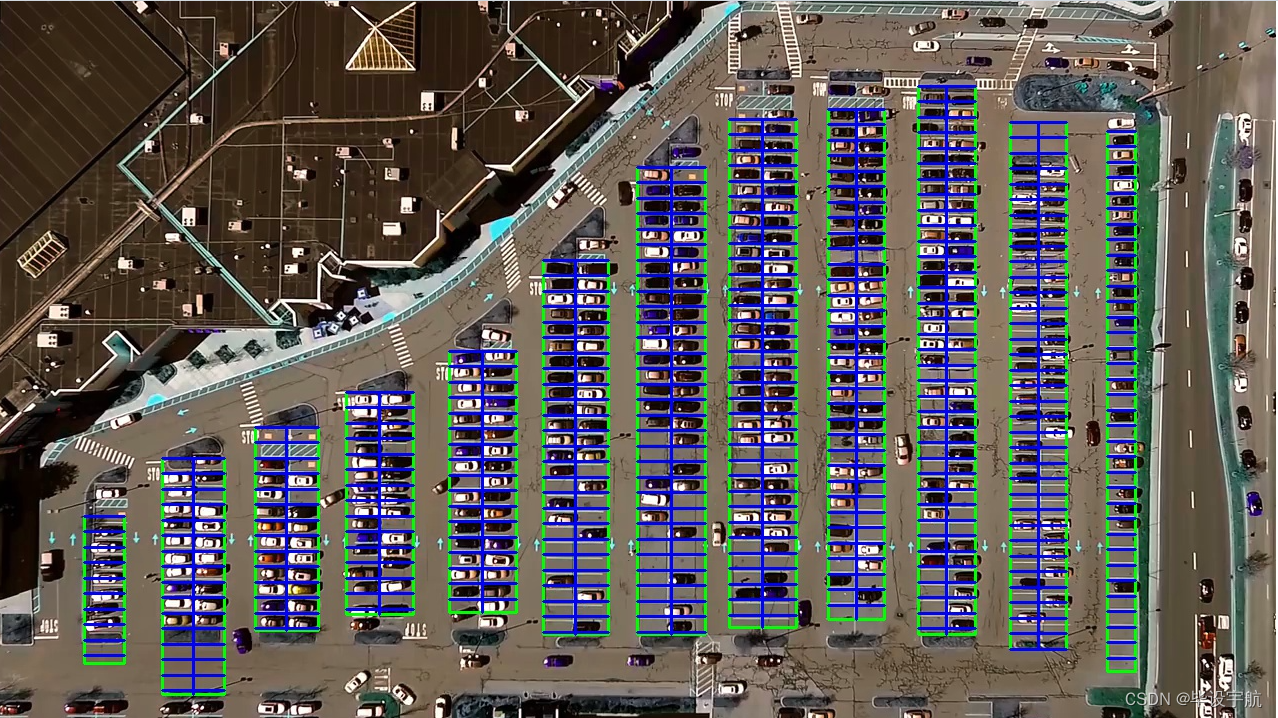
基于OpenCV与Keras的停车场车位自动识别系统
本项目旨在利用计算机视觉技术和深度学习算法,实现对停车场车位状态的实时自动识别。通过摄像头监控停车场内部,系统能够高效准确地辨认车位是否被占用,为车主提供实时的空闲车位信息,同时为停车场管理者提供智能化的车位管理工具…...

YOLOv10改进教程|C2f-CIB加入注意力机制
一、 导读 论文链接:https://arxiv.org/abs/2311.11587 代码链接:GitHub - CV-ZhangXin/AKConv YOLOv10训练、验证及推理教程 二、 C2f-CIB加入注意力机制 2.1 复制代码 打开ultralytics->nn->modules->block.py文件,复制SE注意力机…...
)
算法训练营day06 哈希表(统计数,去重,降低时间复杂度)
💡 解题思路 📝 确定输入与输出🔍 分析复杂度🔨 复杂题目拆分 :严谨且完整 地拆分为更小的子问题(哈希表的使用场景)–(多总结)💭 选择处理逻辑:…...

影帝郭晋安关联保健品企业,草姬集团无研发费用销售成本不低
《港湾商业观察》黄懿 5月30日,草姬集团控股有限公司(下称“草姬集团”)递表港交所主板,农银国际为其独家保荐人。 草姬集团成立于1999年,是中国香港多元化保健品、美容与护肤品供应商,由TVB港星郭晋安及…...
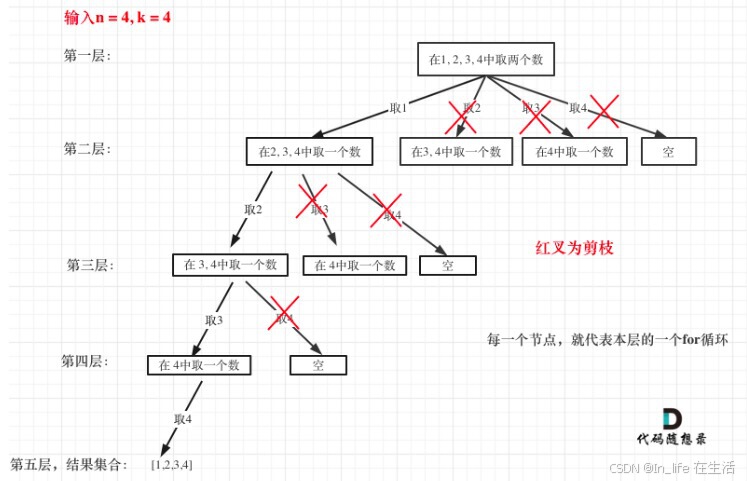
leetcode-19-回溯-组合问题(剪枝、去重)
引自代码随想录 一、[77]组合 给定两个整数 n 和 k,返回 1 ... n 中所有可能的 k 个数的组合。 示例: 输入: n 4, k 2 输出: [ [2,4], [3,4], [2,3], [1,2], [1,3], [1,4]] 1、大致逻辑 k为树的深度,到叶子节点的路径即为一个结果 开始索引保证不…...
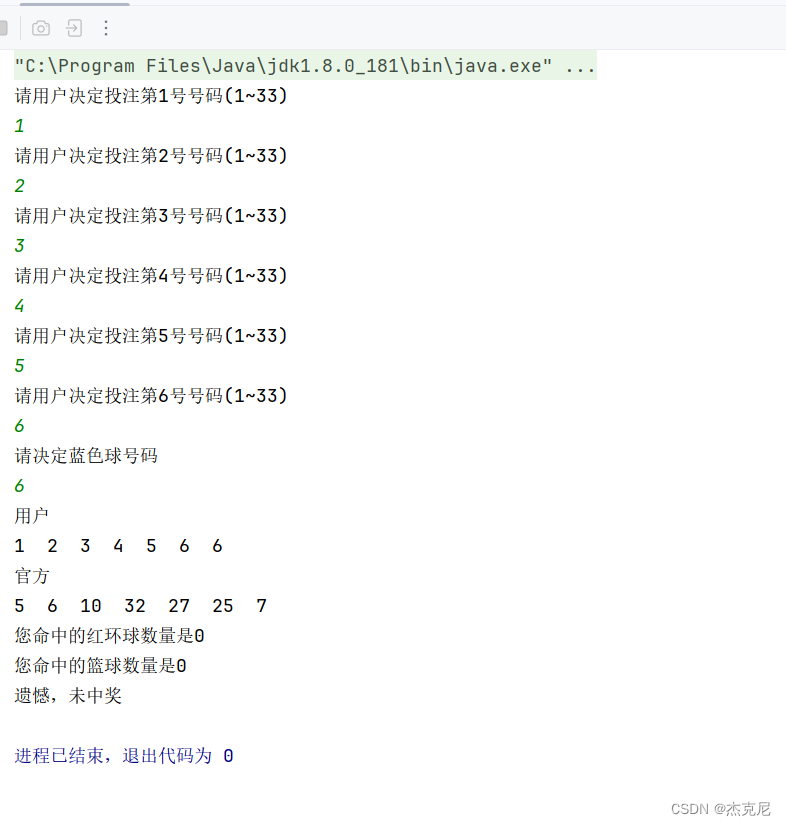
Java案例实现双色球
一问题: 二具体代码: package 重修;import java.util.Random; import java.util.Scanner;public class first {public static void main(String[] args) {int []usersnumbersusernumslect();System.out.println("用户");for (int i 0; i <…...
JS(JavaScript)的BOM操作
天行健,君子以自强不息;地势坤,君子以厚德载物。 每个人都有惰性,但不断学习是好好生活的根本,共勉! 文章均为学习整理笔记,分享记录为主,如有错误请指正,共同学习进步。…...

【CT】LeetCode手撕—82. 删除排序链表中的重复元素 II
题目 原题连接:82. 删除排序链表中的重复元素 II 1- 思路 模式识别1:已排序链表 ——> 判重逻辑 ,涉及到 while 2- 实现 ⭐82. 删除排序链表中的重复元素 II——题解思路 class Solution {public ListNode deleteDuplicates(ListNode h…...

C++ STL unique_ptr智能指针源码剖析
由于上一篇博客将shared_ptr,weak_ptr,enable_shared_form_this的源码实现整理了一遍,想着cpp智能指针还差个unique_ptr故写下此篇博客,以供学习 源码剖析 一,模板参数 首先,我们先看unique_ptr的模板参数,第一个参数_TP自是不用说表示对象类型,第二个模板参数定义了unique_p…...
)
Unity中的的文件夹(特殊文件夹)
Unity中的的文件夹(特殊文件夹) Unity工程中的关键文件夹和路径知识点, 以下是对Unity工程中几个关键文件夹和路径的总结: 1. 工程路径获取 print(Application.dataPath) 用途:通常只在编辑模式下使用。注意事项:游戏发布后࿰…...

Go语言定时器Timer和Ticker到底怎么用
原文链接,可获取更多Go语言学习资料 概述 在日常开发中,我们不可避免的需要使用到定时任务用来处理业务逻辑。在Go语言中内置的有两个定时器,Timer和Ticker,合理的使用这两个定时器可以很好的解决定时任务的需求,同时…...

41、web基础和http协议
web基础与http协议 一、web web:就是我们所说得页面,打开网页展示得页面。(全球广域网,万维网) world wide webwww 分布式图形信息系统 http:超文本传输协议 https:加密的超文本传输协议…...

6-173 二分查找的关键字比较次数
6-173 二分查找的关键字比较次数 - (32)专科段数据结构专项练习(2024版) (pintia.cn) int CountSearchTimes(int a[], int low, int high, int x) {int time0;while(low < high){int mid(lowhigh)/2;time;if(a[mid]x)return t…...

【基础篇】第5章 Elasticsearch 数据聚合与分析
在Elasticsearch的庞大功能体系中,数据聚合与分析扮演着至关重要的角色,它使我们能够从海量数据中提炼出有价值的信息,为决策提供依据。本章将深入探讨Elasticsearch的聚合功能,从基本概念到常见类型的实践,让你掌握如…...
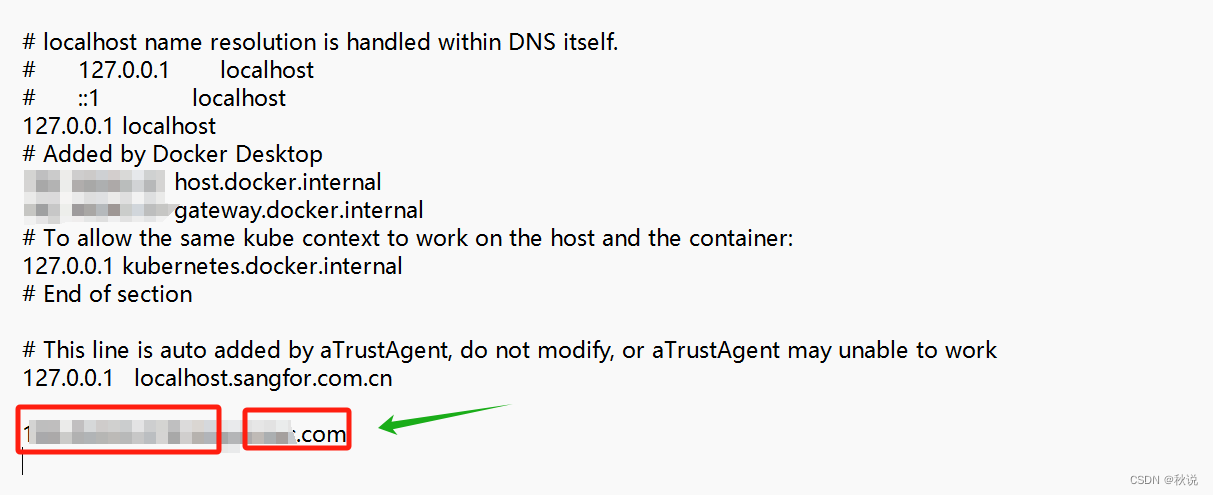
【网络安全】修改Host文件实现域名解析
场景 开发一个网站或者服务,需要在本地测试时,可以将线上的域名指向本地开发环境的IP地址。从而模拟真实环境中的域名访问,方便调试和开发。 步骤 1、以管理员身份打开命令提示符 2、编辑hosts文件: 输入以下命令打开hosts文…...

Spring Boot 全面解析:从入门到实践案例
引言: Spring Boot 是由 Pivotal 团队提供的全新框架,旨在简化 Spring 应用的初始搭建以及开发过程。它基于 Spring 平台,通过“约定优于配置”的原则,尽可能自动化配置,减少XML配置,使得开发者能够快速启…...

222222222
2222222...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...
