C语言实现快速排序(hoare法、挖坑法、前后指针法与非递归实现)——不看后悔系列

目录
1. hoare法
方法与步骤
代码实现
2. 挖坑法
方法与步骤
代码实现
3. 前后指针法
方法与步骤
代码实现
4. 快速排序的缺点与优化
1.快速排序的缺点
2.快速排序的优化
① 三数取中法选 key
代码实现
② 小区间优化
代码实现
5. 快速排序的非递归实现
附录﹡完整源码
快速排序递归实现
快速排序非递归实现
快速排序是霍尔大佬在1962年提出的排序方法,因其出色的排序效率使得它成为使用最广泛的排序算法。快速排序之所以敢叫做快速排序,自然是有一定的道理,今天我们就来看看快速排序是如何凌驾于其它算法之上的。
快速排序的基本思想是:任取待排序数列中的一个数作为 key 值,通过某种方法使得 key 的左边所有的数都比它小,右边的数都比它大;以 key 为中心,将 key 左边的数列与右边的数列取出,做同样的操作(取 key 值,分割左右区间),直至所有的数都到了正确的位置。
上述所提到的某种方法可以有很多种,例如:hoare法、挖坑法、前后指针法。它们虽然做法不相同,但做的都是同一件事——分割出 key 的左右区间(左边的数比 key 小,右边的数比 key 大)。
我们首先来看看霍尔大佬所用的方法——hoare法。
1. hoare法
方法与步骤
以数列 6,1,2,7,9,3,4,5,8,10 为例:
 1.取最左边为 key ,分别有 left 和 right 指向数列的最左端与最右端;
1.取最左边为 key ,分别有 left 和 right 指向数列的最左端与最右端;

2. right 先走,找到比 key 小的数就停下来;

3. left 开始走,找到比 key 大的数就停下来;

4. 交换 left 与 right 所在位置的数;

5.重复上述操作,right 找小,left 找大,进行交换;

6. right 继续找小;

7. left 继续找大,若与 right 就停下来;
8.交换二者相遇位置与 key 处的值;

此时一趟排序就完成了,此时的数列有两个特点:
1. key 所指向的值(6)已经到了正确的位置;
2. key 左边的数字都比 key 要小,右边的都比 key 要大;
接下来就是递归的过程了,分别对左右区间进行同样的操作:

代码实现
知道了详解步骤,用代码来实现并不困难,但是有很多很多的细节需要注意。(这里的代码未经优化,当前的代码有几种极端的情况不能适应)
void Swap(int* p, int* q)
{int tmp = *p;*p = *q;*q = tmp;
}void QuickSort(int* a, int begin, int end)
{//数列只有一个数,或无数列则返回if (begin >= end){return;}int left = begin;int right = end;int keyi = left;while (left < right){//右边先走while (left < right && a[right] >= a[keyi]){right--;}while (left < right && a[left] <= a[keyi]){left++;}Swap(&a[left], &a[right]);}Swap(&a[keyi], &a[left]);QuickSort(a, begin, left - 1);QuickSort(a, left + 1, end);
}2. 挖坑法
挖坑法相比于hoare法,思路上更为简单易懂。
方法与步骤
还是以同样的数列 6,1,2,7,9,3,4,5,8,10 为例:

1. 先将第一个数存放到 key 中,形成一个坑位:分别有 left 和 right 指向数列的最左端与最右端;

2. right 先走,找到比 key 小的数,将该数丢到坑里;同时又形成了一个新的坑;

3. left 开始走,找到比 key 大的数,将该数丢到坑里;同时形成一个新的坑;

4. right继续找小,进行重复的操作;

5. left 找大;
 6. right 找小;
6. right 找小;
 7. left 找大;
7. left 找大;
8.若二者相遇就停下来;将 key 值放入坑;

至此,一趟排序已经完成,我们发现此时的数列与hoare具有相同的特点:
1. key 所指向的值(6)已经到了正确的位置;
2. key 左边的数字都比 key 要小,右边的都比 key 要大;
挖坑法、hoare、前后指针法完成一趟排序后都具有相同的特点,所以不同版本的快速排序不一样的只有单趟排序的实现,总体思路都是相同的。
代码实现
void QuickSort(int* a, int begin, int end)
{if (begin >= end){return;}int left = begin;int right = end;int key = a[left];int hole = left;//坑位while (left < right){while (left < right && a[right] >= key){right--;}a[hole] = a[right];hole = right;while (left < right && a[left] <= key){left++;}a[hole] = a[left];hole = left;}a[hole] = key;QuickSort(a, begin, hole - 1);QuickSort(a, hole + 1, end);
}3. 前后指针法
方法与步骤
以同样的数列为例:
 1. 取第一个值为 key ;有 prev 和 cur 分别指向数列开头和 prev 的下一个数;
1. 取第一个值为 key ;有 prev 和 cur 分别指向数列开头和 prev 的下一个数;
 2. cur 先走,找到比 key 小的数就停下来;
2. cur 先走,找到比 key 小的数就停下来;
3. ++prev ,交换 prev 与 cur 位置的数;(前两次无需交换,因为自己与自己换没有意义)
 4. 重复此步骤;
4. 重复此步骤;
 5. 直到 cur 走完整个数列,交换 prev 与 key 处的值;
5. 直到 cur 走完整个数列,交换 prev 与 key 处的值;

至此,第一趟排序就结束了,又是与前两种方法相同的结果;
代码实现
void QuickSort(int* a, int begin, int end)
{if (begin >= end){return;}int prev = begin;int cur = prev + 1;int keyi = begin;while (cur <= end){if (a[cur] < a[keyi] && ++prev != cur){Swap(&a[prev], &a[cur]);}cur++;}Swap(&a[keyi], &a[prev]);keyi = prev;QuickSort(a, begin, keyi - 1);QuickSort(a, keyi + 1, end);
}4. 快速排序的缺点与优化
1.快速排序的缺点
我们用三种方式实现了快速排序,其实这三种方式并无明显的优劣之分。但是我们前面设计的快速排序其实是有两个缺点的:
1.在最坏情况下它的的效率极慢;
2.在数据量太大时会造成栈溢出。
那么什么情况是最坏情况呢?答案是,当数据本身就是有序的时候(无论是逆序还是顺序)。在最坏情况下,每次我们的 key 值都是最大或者最小,这样就会使 key 与数列的每个数都比较一次,它的时间复杂度为 O(n^2);
为什么会发生栈溢出呢?因为我们的快速排序是利用递归实现的,有递归调用,就要建立函数栈帧,并且随着递归的深度越深所要建立的函数栈帧的消耗就越大 。如这幅图所示:

2.快速排序的优化
① 三数取中法选 key
为了应对最坏情况会出现时间复杂度为 O(N^2) 的情况,有人提出了三数取中的方法。
旧方法中,我们每次选 key 都是数列的第一个元素。三数取中的做法是,分别取数列的第一个元素、最后一个元素和最中间的元素,选出三个数中不是最大也不是最小的那个数当作 key 值。
有了三数取中,之前的最坏情况立马变成了最好情况。
代码实现
由于hoare法、挖坑法、前后指针法最终的效果都相同且效率差异很小,所以就任意选取一个为例,其余两者都类似。
//三数取中的函数
int GetMidIndex(int* a, int begin, int end)
{int mid = (begin + end) / 2;if (a[begin] < a[mid]){if (a[mid] < a[end]){return mid;}else if (a[begin] > a[end]){return begin;}else{return end;}}else // a[begin] > a[mid]{if (a[mid] > a[end]){return mid;}else if (a[begin] < a[end]){return begin;}else{return end;}}
}
//hoare法
void QuickSort(int* a, int begin, int end)
{if (begin >= end){return;}int mid = GetMidIndex(a, begin, end);Swap(&a[mid], &a[begin]);int left = begin;int right = end;int keyi = left;while (left < right){while (left < right && a[right] >= a[keyi]){right--;}while (left < right && a[left] <= a[keyi]){left++;}Swap(&a[left], &a[right]);}Swap(&a[keyi], &a[left]);QuickSort(a, begin, left - 1);QuickSort(a, left + 1, end);
}
② 小区间优化
随着递归的调用越深入,此时有个很大的缺点就是函数栈帧的消耗很大。但是同时又有一个好处,就是越往下,数列就越接近有序,且此时每个小区间的数据个数特别少。
那么有什么办法可以取其长处避其短处呢?不知道你是否还记得插入排序的特点——数据越接近有序,效率就越高。并且,在数据量极少的情况下,时间复杂度为 O(N^2) 的插入排序与时间复杂度为 O(N*log N) 的快速排序基本没有什么区别。所以,我们干脆就在排序数据量少的数列时,采用插入排序代替。
代码实现
//三数取中的函数
int GetMidIndex(int* a, int begin, int end)
{int mid = (begin + end) / 2;if (a[begin] < a[mid]){if (a[mid] < a[end]){return mid;}else if (a[begin] > a[end]){return begin;}else{return end;}}else // a[begin] > a[mid]{if (a[mid] > a[end]){return mid;}else if (a[begin] < a[end]){return begin;}else{return end;}}
}//插入排序
void InsertSort(int* a, int n)
{for (int i = 0; i < n - 1; i++){int end = i;int tmp = a[end + 1];while (end >= 0){if (a[end] > tmp) //大于tmp,往后挪一个{a[end + 1] = a[end];end--;}else{break;}}a[end + 1] = tmp; //把tmp插入空隙}
}//hoare法
void QuickSort(int* a, int begin, int end)
{if (begin >= end){return;}if ((end - begin + 1) < 15){// 小区间用直接插入替代,减少递归调用次数InsertSort(a+begin, end - begin + 1);}else{int mid = GetMidIndex(a, begin, end);Swap(&a[mid], &a[begin]);int left = begin;int right = end;int keyi = left;while (left < right){while (left < right && a[right] >= a[keyi]){right--;}while (left < right && a[left] <= a[keyi]){left++;}Swap(&a[left], &a[right]);}Swap(&a[keyi], &a[left]);QuickSort(a, begin, left - 1);QuickSort(a, left + 1, end);}
}
两外两种方法的代码实现已打包完成,可在文末直接取用。
5. 快速排序的非递归实现
快速排序的非递归思路与递归相差无几,唯一不同的是,非递归用栈或队列模拟函数递归建立栈帧的过程。
void QuickSortNonR(int* a, int begin, int end)
{Stack st;StackInit(&st);StackPush(&st, begin);StackPush(&st, end);while (!StackEmpty(&st)){int right = StackTop(&st);StackPop(&st);int left = StackTop(&st);StackPop(&st);int keyi = PartSort1(a, left, right);//三种方法任选其一//int keyi = PartSort2(a, left, right);//int keyi = PartSort3(a, left, right);if (keyi + 1 < right){StackPush(&st, keyi + 1);StackPush(&st, right);}if (left < keyi - 1){StackPush(&st, left);StackPush(&st, keyi - 1);}}StackDestroy(&st);
}附录﹡完整源码
快速排序递归实现
//交换函数
void Swap(int* p, int* q)
{int tmp = *p;*p = *q;*q = tmp;
}//三数取中
int GetMidIndex(int* a, int begin, int end)
{int mid = (begin + end) / 2;if (a[begin] < a[mid]){if (a[mid] < a[end]){return mid;}else if (a[begin] > a[end]){return begin;}else{return end;}}else // a[begin] > a[mid]{if (a[mid] > a[end]){return mid;}else if (a[begin] < a[end]){return begin;}else{return end;}}
}//插入排序
void InsertSort(int* a, int n)
{for (int i = 0; i < n - 1; i++){int end = i;int tmp = a[end + 1];while (end >= 0){if (a[end] > tmp) //大于tmp,往后挪一个{a[end + 1] = a[end];end--;}else{break;}}a[end + 1] = tmp; //把tmp插入空隙}
}// Hoare法
int PartSort1(int* a, int begin, int end)
{int mid = GetMidIndex(a, begin, end);Swap(&a[begin], &a[mid]);int left = begin, right = end;int keyi = left;while (left < right){while (left < right && a[right] >= a[keyi]){--right;}while (left < right && a[left] <= a[keyi]){++left;}Swap(&a[left], &a[right]);}Swap(&a[left], &a[keyi]);keyi = left;return keyi;
}// 挖坑法
int PartSort2(int* a, int begin, int end)
{int mid = GetMidIndex(a, begin, end);Swap(&a[begin], &a[mid]);int left = begin, right = end;int key = a[left];int hole = left;while (left < right){while (left < right && a[right] >= key){--right;}a[hole] = a[right];hole = right;while (left < right && a[left] <= key){++left;}a[hole] = a[left];hole = left;}a[hole] = key;return hole;
}//前后指针法
int PartSort3(int* a, int begin, int end)
{int mid = GetMidIndex(a, begin, end);Swap(&a[begin], &a[mid]);int keyi = begin;int prev = begin, cur = begin + 1;while (cur <= end){if (a[cur] < a[keyi] && ++prev != cur)Swap(&a[prev], &a[cur]);++cur;}Swap(&a[prev], &a[keyi]);keyi = prev;return keyi;
}//快速排序(递归)
void QuickSort(int* a, int begin, int end)
{if (begin >= end){return;}if ((end - begin + 1) < 15){// 小区间用直接插入替代,减少递归调用次数InsertSort(a + begin, end - begin + 1);}else{int keyi = PartSort1(a, begin, end);//int keyi = PartSort2(a, begin, end);//int keyi = PartSort3(a, begin, end);QuickSort(a, begin, keyi - 1);QuickSort(a, keyi + 1, end);}
}快速排序非递归实现
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>typedef int STDataType;typedef struct Stack
{STDataType* a; //动态开辟数组int capacity; //记录栈的容量大小int top; //记录栈顶的位置
}Stack;//栈的初始化
void StackInit(Stack* ps);
//释放动态开辟的内存
void StackDestroy(Stack* ps);
//压栈
void StackPush(Stack* ps, STDataType data);
//出栈
void StackPop(Stack* ps);
//读取栈顶的元素
STDataType StackTop(Stack* ps);
//判断栈是否为空
bool StackEmpty(Stack* ps);// Hoare法
int PartSort1(int* a, int begin, int end)
{int mid = GetMidIndex(a, begin, end);Swap(&a[begin], &a[mid]);int left = begin, right = end;int keyi = left;while (left < right){while (left < right && a[right] >= a[keyi]){--right;}while (left < right && a[left] <= a[keyi]){++left;}Swap(&a[left], &a[right]);}Swap(&a[left], &a[keyi]);keyi = left;return keyi;
}// 挖坑法
int PartSort2(int* a, int begin, int end)
{int mid = GetMidIndex(a, begin, end);Swap(&a[begin], &a[mid]);int left = begin, right = end;int key = a[left];int hole = left;while (left < right){while (left < right && a[right] >= key){--right;}a[hole] = a[right];hole = right;while (left < right && a[left] <= key){++left;}a[hole] = a[left];hole = left;}a[hole] = key;return hole;
}int PartSort3(int* a, int begin, int end)
{int mid = GetMidIndex(a, begin, end);Swap(&a[begin], &a[mid]);int keyi = begin;int prev = begin, cur = begin + 1;while (cur <= end){if (a[cur] < a[keyi] && ++prev != cur)Swap(&a[prev], &a[cur]);++cur;}Swap(&a[prev], &a[keyi]);keyi = prev;return keyi;
}
void QuickSortNonR(int* a, int begin, int end)
{Stack st;StackInit(&st);StackPush(&st, begin);StackPush(&st, end);while (!StackEmpty(&st)){int right = StackTop(&st);StackPop(&st);int left = StackTop(&st);StackPop(&st);int keyi = PartSort1(a, left, right);//三种方法任选其一//int keyi = PartSort2(a, left, right);//int keyi = PartSort3(a, left, right);if (keyi + 1 < right){StackPush(&st, keyi + 1);StackPush(&st, right);}if (left < keyi - 1){StackPush(&st, left);StackPush(&st, keyi - 1);}}StackDestroy(&st);
}//栈的实现_函数定义void StackInit(Stack* ps)
{assert(ps);//初始化时,可附初值,也可置空ps->a = NULL;ps->capacity = 0;ps->top = 0;
}void StackDestroy(Stack* ps)
{assert(ps);//若并未对ps->a申请内存,则无需释放if (ps->capacity == 0)return;//释放free(ps->a);ps->a = NULL;ps->capacity = ps->top = 0;
}void StackPush(Stack* ps,STDataType data)
{assert(ps);//若容量大小等于数据个数,则说明栈已满,需扩容if (ps->capacity == ps->top){//若为第一次扩容,则大小为4,否则每次扩大2倍int newCapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;STDataType* tmp = (STDataType*)realloc(ps->a, sizeof(STDataType) * newCapacity);if (tmp == NULL){perror("realloc fail");exit(-1);}ps->a = tmp;ps->capacity = newCapacity;}//压栈ps->a[ps->top] = data;ps->top++;
}void StackPop(Stack* ps)
{assert(ps);assert(!StackEmpty(ps));//出栈ps->top--;
}STDataType StackTop(Stack* ps)
{assert(ps);assert(!StackEmpty(ps));//返回栈顶的数据return ps->a[ps->top - 1];
}bool StackEmpty(Stack* ps)
{assert(ps);//返回topreturn ps->top == 0;
}相关文章:

C语言实现快速排序(hoare法、挖坑法、前后指针法与非递归实现)——不看后悔系列
目录 1. hoare法 方法与步骤 代码实现 2. 挖坑法 方法与步骤 代码实现 3. 前后指针法 方法与步骤 代码实现 4. 快速排序的缺点与优化 1.快速排序的缺点 2.快速排序的优化 ① 三数取中法选 key 代码实现 ② 小区间优化 代码实现 5. 快速排序的非递归实现 附录…...

如何为系统可靠性的量化提供依据
SLA 即 Service Level Agreement,也就是服务等级协议,它指的是系统服务提供者(Provider)对客户(Customer)的一个服务承诺。 而 SLO 就是 SLA 的具体目标管理办法,它由一系列相关的指标 SLI &am…...

量化投资中的因子是什么?因子是如何分类的,包括哪些?
因子就是对个股有解释的因素。因子的种类很多,不同类别的因子从不同的维度对个股收益进行解释。比如基本面因子的数据来源方面有很大一部分是财务报表,从估值、成长、盈利能力等多个方面对股票收益进行解释。量价因子是围绕价格、成交量等技术指标构建的…...

力扣-修复表中的名字
大家好,我是空空star,本篇带大家了解一道简单的力扣sql练习题。 文章目录前言一、题目:1667. 修复表中的名字二、解题1.正确示范①提交SQL运行结果2.正确示范②提交SQL运行结果3.正确示范③提交SQL运行结果4.正确示范④提交SQL运行结果5.其他…...

【博客633】linux vxlan设备工作原理
linux vxlan设备工作原理 vxlan处理包的原理:以k8s cni flannel组件创建的vxlan设备为例 1、k8s cni组件创建flannel设备flannel.1,且这个设备为vxlan类型的设备 root10.10.10.12:/home/ubuntu# ethtool -i flannel.1 driver: vxlan version: 0.1 fi…...

3.12学习周报
文章目录前言文献阅读摘要简介方法介绍讨论结论相关性分析总结前言 本周阅读文献《Streamflow and rainfall forecasting by two long short-term memory-based models》,文献主要提出两种基于长短时记忆网络的混合模型用于对水流量和降雨量进行预测。小波-LSTM&am…...
电力电子中逐波限流控制以及dsp实现
逐波限流是指在电力系统运行中,对电力设备进行电流保护的一种措施。它的实现方式是通过对电力系统的电流进行逐波监测和控制,每一波电流都可以独立地进行限制,从而保护电力系统设备不受过载损坏或短路故障的影响。 逐波限流的作用是提高电力…...
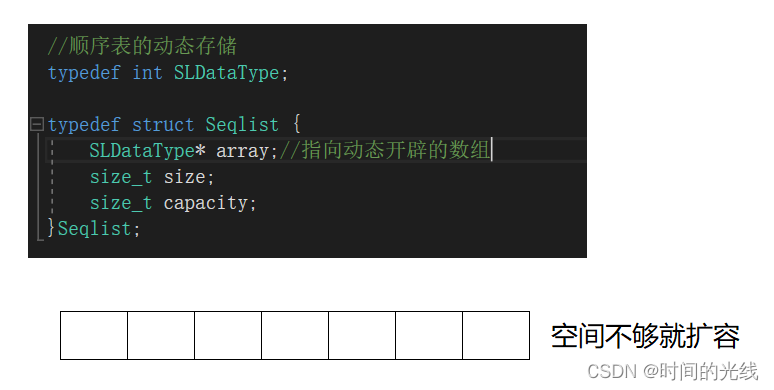
【数据结构】 顺序表
文章目录1 线性表2 顺序表2.1 概念及结构2.2 接口实现2.3 数组相关面试题2.4 顺序表的问题与思考1 线性表 线性表(linear list)是n个具有相同特性的数据元素的有限序列。线性表是一种在实际中广泛使用的数据结构,常见的线性表:顺序…...

Elasticsearch 集群规划- 单台机器核心数计算公式
在做集群规划的时候,到底需要给集群的每个节点多少个核心数?这个问题一直困扰了我很久。最近一段时间做千亿数据,PB存储量集群规划的时候,突然想明白了这件事,大致可以用一个公式来计算!我觉得这是一个非常…...

Tesla都使用什么编程语言?
作者 | 初光 出品 | 车端 备注 | 转载请阅读文中版权声明 知圈 | 进“汽车电子与AutoSAR开发”群,请加微“cloud2sunshine” 总目录链接>> AutoSAR入门和实战系列总目录 带着对更美好未来的愿景,特斯拉不仅成为有史以来最有价值的汽车公司&…...

1143. 最长公共子序列——【Leetcode每日刷题】
1143. 最长公共子序列 给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。 一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些…...
、obj.notify()、obj.notifyAll()详解)
【并发基础】线程的通知与等待:obj.wait()、obj.notify()、obj.notifyAll()详解
目录 〇、先总结一下这三个方法带来的Java线程状态变化 一、obj.wait() 1.1 作用 1.2 使用前需要持有线程共享对象的锁 1.3 使用技巧 二、obj.notify(All)() 1.1 notify() 方法 1.1.1 调用notify()或notifyAll()不会释放线程的锁 1.2 notifyAll() 方法 1.3 使用技巧 三、使用实…...

css黏性定位-实现商城的分类滚动的标题吸附
传统的黏性定位是使用js通过计算高度来实现的,当元素滚动到一定位置时吸附在当前位置。下面我们通过css来实现黏性定位功能。 黏性定位 黏性定位目前主流的浏览器已经全部支持,顾名思义,黏性定位具有吸附的效果,其实它是positio…...

@Component和@bean注解在容器中创建实例区别
Component和Bean的区别 在Spring Boot中,Component注解和Bean注解都可以用于创建bean。它们的主要区别在于它们的作用范围和创建方式。 Component注解是一种通用的注解,可以用于标注任何类。被标注的类将被Spring容器自动扫描并创建为一个bean。这个bea…...

不写注释就是垃圾
最近Linux6.2出来了增加了很多新的东西,有看点的是,Linux确实要可以在Apple M1上面运行了,这应该是一个很大的新闻,如果有这么稳定的硬件支持,那对于Linux来说相当于又打下了一大片的江山。其中关于Linux6.2的特性罗列…...

深信服一面
1.C变量存储在哪里,生命周期是怎样的 2.静态成员变量和成员函数的特性,在哪里用过吗 3.new和delete是什么,和malloc和free对比有啥优势 4.new能不能重载,重载new有什么用 5.多态是怎么实现的,有什么优势和目的 6.…...

【C语言】深度理解指针(中)
前言✈上回说到,我们学习了一些与指针相关的数据类型,如指针数组,数组指针,函数指针等等,我们还学习了转移表的基本概念,学会了如何利用转移表来实现一个简易计算器。详情请点击传送门:【C语言】…...

步进电机运动八大算法
引导一种模块化(Module)设计思想,将传统步进电机的控制器(controller)、驱动器(Driver)、运动算法(Arithmetic)三合一。 对比国内外步进电机驱动原理和已有工作,结合各种硬件特性,改进或实现了可实际移植并用于步进电机控制八大算法。本产品…...

如果你持续大量的教坏ChatGPT,它确实会变坏
你输出的很多数据是经过人工标注吗,以确保可以正常对外展示出来,而不是有性别歧视、种族歧视或者其它意识形态为多数人所不认同的内容产生? 作为AI语言模型,我并不直接处理或输出任何数据,我的任务是通过对输入的自然语…...

opencv学习(二)图像阈值和平滑处理
图像阈值ret, dst cv2.threshold(src, thresh, maxval, type)src: 输入图,只能输入单通道图像,通常来说为灰度图dst: 输出图thresh: 阈值maxval: 当像素值超过了阈值(或者小于阈值,…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...
