【C语言题目】34.猜凶手
文章目录
- 作业标题
- 作业内容
- 2.解题思路
- 3.具体代码
作业标题
猜凶手
作业内容
日本某地发生了一件谋杀案,警察通过排查确定杀人凶手必为4个嫌疑犯的一个。
以下为4个嫌疑犯的供词:
A说:不是我。
B说:是C。
C说:是D。
D说:C在胡说
已知3个人说了真话,1个人说的是假话。
现在请根据这些信息,写一个程序来确定到底谁是凶手。
2.解题思路
简单的说,就是3个人说真话,1个人说假话,来判断凶手是谁。
提取ABCD说的关键信息:不是A,是C,是D,不是D
这里形容的都是凶手,也就是把凶手和这些信息对比,就可以了。
3.具体代码
#include <stdio.h>int main()
{char killer;for(killer='A'; killer<='D'; killer++)//巧妙地利用ASCII 从A-D进行循环和比较{//下面分别对应每个人都供词 不是A 是C 是D 不是Dif (((killer!='A') + (killer=='C') + (killer=='D') + (killer!='D'))==3) //这里等于3表示 有三个人说了真话{printf("%c是凶手\n",killer);break;}}return 0;
}
打印:

相关文章:

【C语言题目】34.猜凶手
文章目录 作业标题作业内容2.解题思路3.具体代码 作业标题 猜凶手 作业内容 日本某地发生了一件谋杀案,警察通过排查确定杀人凶手必为4个嫌疑犯的一个。 以下为4个嫌疑犯的供词: A说:不是我。 B说:是C。 C说:是D。 D说ÿ…...

C++ 多进程多线程间通信
目录 一、进程间通信 1、管道(Pipe) 2、消息队列(Message Queue) 3、共享内存(Shared Memory) 4、信号量(Semaphore) 5、套接字(Socket) 6、信号&…...

怎么做防御系统IPS
入侵防御系统(IPS)是入侵检测系统(IDS)的增强版本,它不仅检测网络流量中的恶意活动,还能自动采取措施阻止这些活动。实现IPS的主要工具包括Snort和Suricata。以下是使用Snort和Suricata来实现IPS的详细步骤…...

达梦数据库的系统视图v$auditrecords
达梦数据库的系统视图v$auditrecords 在达梦数据库(DM Database)中,V$AUDITRECORDS 是专门用来存储和查询数据库审计记录的重要系统视图。这个视图提供了对所有审计事件的访问权限,包括操作类型、操作用户、时间戳、目标对象等信…...

Spring Boot与MyBatis-Plus:代码逆向生成指南
在Spring Boot项目中使用MyBatis-Plus进行代码逆向生成,可以通过MyBatis-Plus提供的代码生成器来快速生成实体类、Mapper接口、Service接口及其实现类等。以下是一个简单的示例步骤: 代码逆向生成 1.添加依赖: 在pom.xml文件中添加MyBati…...
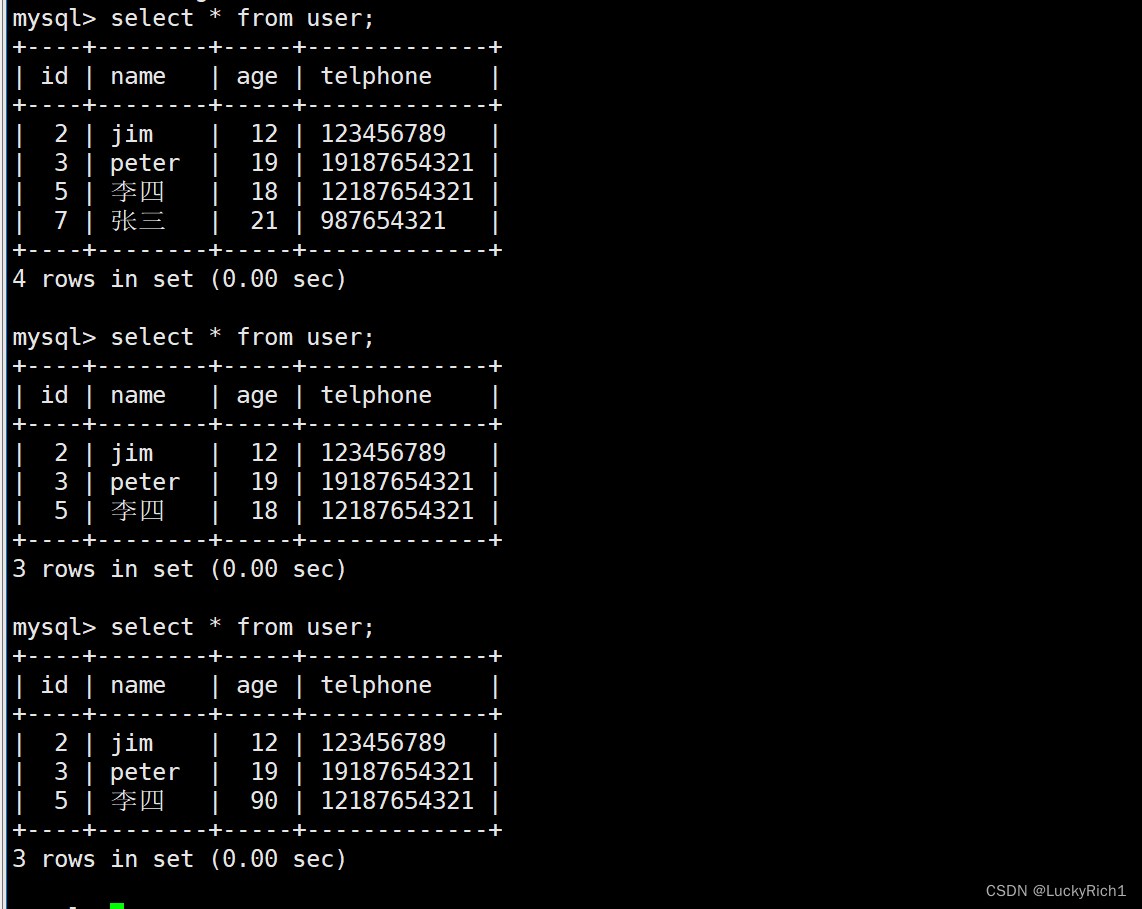
【MySQL】mysql访问
mysql访问 1.引入MySQL 客户端库2.C/C 进行增删改3.查询的处理细节4.图形化界面访问数据库4.1下载MYSQL Workbench4.2MYSQL Workbench远程连接数据库 点赞👍👍收藏🌟🌟关注💖💖 你的支持是对我最大的鼓励&a…...
(1)Jupyter Notebook 下载及安装
目录 1. Jupyter Notebook是什么?2. Jupyter Notebook特征3. 组成部分3.1 网页应用3.2 文档 4. 适用场景5. 利用Google Colab安装Jupyter Notebook3.1 什么是 Colab?3.2 访问 Google Colab3.3 新建笔记本 1. Jupyter Notebook是什么? 百度百科…...
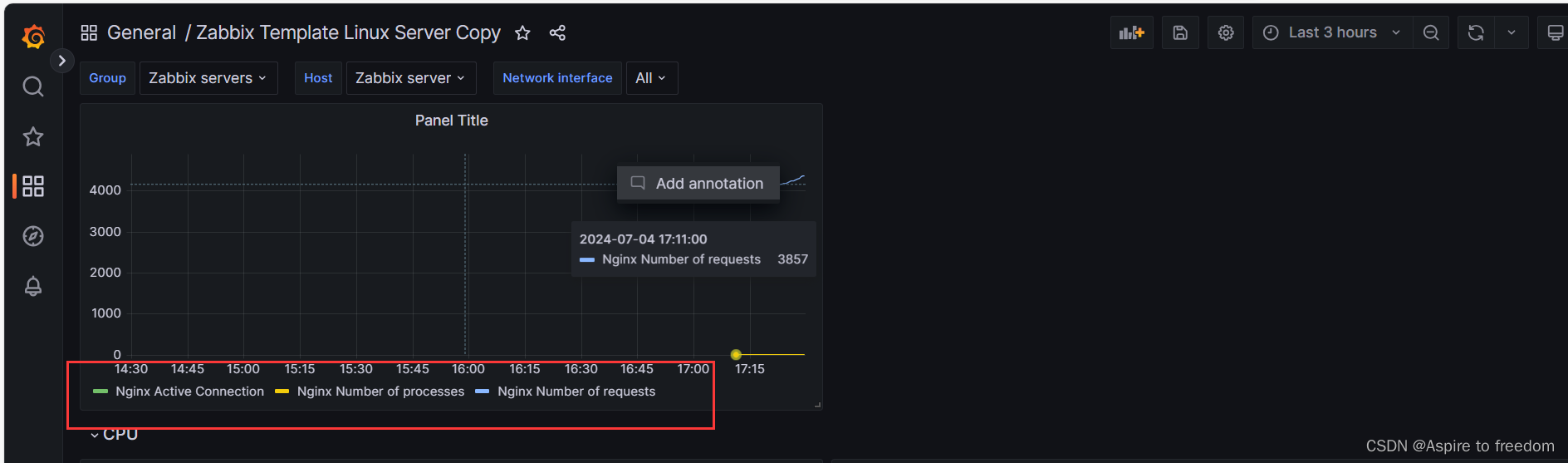
监控平台zabbix对接grafana
本次博客基于监控平台zabbix介绍与部署-CSDN博客的环境下进行的 1、安装grafana并启动 添加一台虚拟机20.0.0.30 (1)系统初始化 [rootzx3 ~]# systemctl stop firewalld [rootzx3 ~]# setenforce 0 [rootzx3 ~]#(2)安装并启动…...

14-11 2024 年的 13 个 AI 趋势
2024 年的 13 个 AI 趋势 人工智能对环境的影响和平人工智能人工智能支持的问题解决和决策针对人工智能公司的诉讼2024 年美国总统大选与人工智能威胁人工智能、网络犯罪和社会工程威胁人工智能治疗孤独与对人工智能的情感依赖人工智能影响者中国争夺人工智能霸主地位人工智能…...

计算机大方向的选择
选专业要了解自己的兴趣所在。 即想要学习什么样的专业,如果有明确的专业意向,就可以有针对性地选择那些专业实力较强的院校。 2.如果没有明确的专业意向,可以优先考虑一下院校。 确定一下自己想要选择综合性院校还是理工类院校或是像财经或者…...

使用Qt Installer Framework在centos7中打包
文章目录 步骤 1: 安装Qt和Qt Installer Framework安装Qt安装Qt Installer Framework步骤 2: 创建项目目录结构步骤 3: 编写安装脚本配置文件(config/config.xml)Package 信息meta/package.xmldata 目录步骤 4: 编写安装脚本步骤 5: 生成安装程序总结在CentOS 7中使用Qt Inst…...

您的私人办公室!-----ONLYOFFICE8.1版本的桌面编辑器测评
随时随地创建并编辑文档,还可就其进行协作 ONLYOFFICE 文档是一款强大的在线编辑器,为您使用的平台提供文本文档、电子表格、演示文稿、表单和 PDF 编辑工具。 网页地址链接: https://www.onlyoffice.com/zh/office-suite.aspxhttps://www…...

点估计和参数分布的对比
点估计(Point Estimation)和 参数分布(Parameter Distribution)是统计学中两种不同的参数估计方法。 文章目录 点估计(Point Estimation)参数分布(Parameter Distribution)对比总结 …...
桌面保存的Word文件删除怎么找回?超实用的三个方法?
在日常工作和学习中,我们经常会使用Word文档进行文字编辑和文件保存。但是,有时由于操作失误或系统故障,我们会不小心将存放在电脑桌面重要的Word文件删除了。导致无法挽回的损失,但幸运的是,有一些方法可以帮助我们找…...

【leetcode】双指针算法题
文章目录 1.算法思想2.移动零3.复写零方法一方法二 4.快乐数5.盛水最多的容器方法一(暴力求解)方法二(左右指针) 6.有效三角形的个数方法一(暴力求解)方法二(左右指针) 7.两数之和8.…...

vue-router 源码分析——8.重定向
这是对vue-router 3 版本的源码分析。 本次分析会按以下方法进行: 按官网的使用文档顺序,围绕着某一功能点进行分析。这样不仅能学习优秀的项目源码,更能加深对项目的某个功能是如何实现的理解。这个对自己的技能提升,甚至面试时…...

CAN总线协议
CAN总线协议,全程为控制器局域网(Controller Area Network)协议,是一种用于实时应用的串行通讯协议。该协议由德国某公司专门为汽车行业开发,并逐渐成为一种标准,这是国际上应用最广泛的现场总线之一。 一…...
NLP篇1
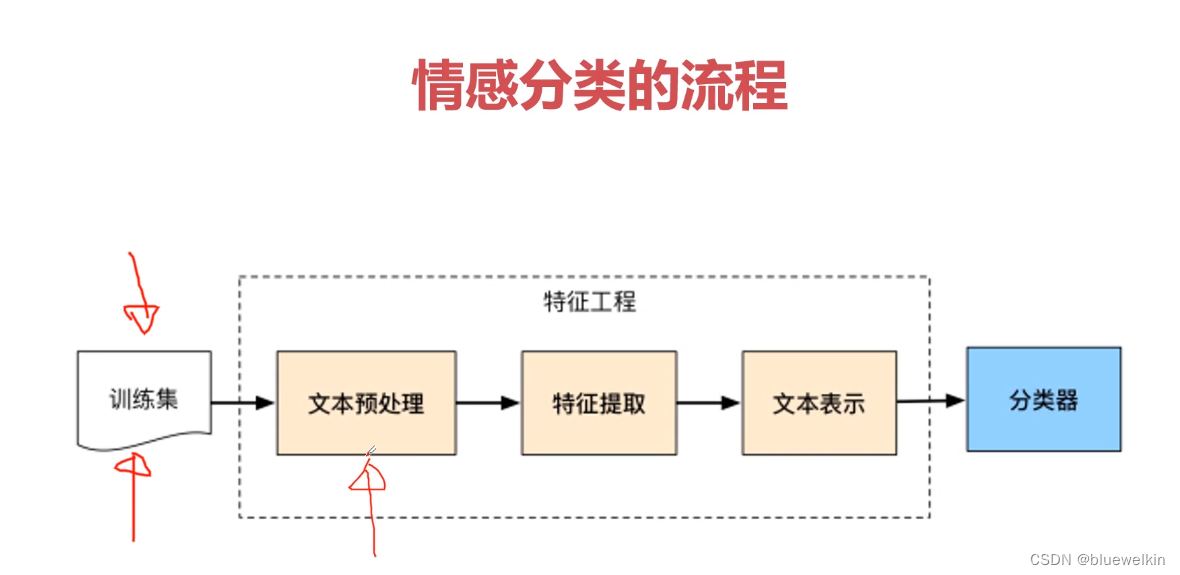
场景:假设给你一篇文章。 目标:说白了,就是数学的分类。但是如何实现分类呢。下面将逐步一 一 分析与拆解。先把目标定好了和整体框架定好了。而不是只见树木而不见森林。 情感分类(好评、差评,中性) 整体…...

【一念发动便是行】念头,就是命运
一个个恶念累积就是负能量,念头就是命运,克除恶念,防范念头,念头都有能量,学圣学须内外庄严检肃,言语有灵 多数人的问题都是出在念头上,念头,就是自己的命运; 当我们对自…...

Django + Vue 实现图片上传功能的全流程配置与详细操作指南
文章目录 前言图片上传步骤1. urls 配置2. settings 配置3. models 配置4. 安装Pillow 前言 在现代Web应用中,图片上传是一个常见且重要的功能。Django作为强大的Python Web框架,结合Vue.js这样的现代前端框架,能够高效地实现这一功能。本文将…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
