WGAN(Wassertein GAN)
WGAN
E x ∼ P g [ log ( 1 − D ( x ) ) ] E x ∼ P g [ − log D ( x ) ] \begin{aligned} & \mathbb{E}_{x \sim P_g}[\log (1-D(x))] \\ & \mathbb{E}_{x \sim P_g}[-\log D(x)] \end{aligned} Ex∼Pg[log(1−D(x))]Ex∼Pg[−logD(x)]
原始 GAN 中判别器; 在 WGAN 两篇论文中称为 “the - log D alternative” 或 “the - log D trick”。WGAN 前作分别分析了这两种形式的原始 GAN 各自的问题所在 .
第一种原始 GAN 形式的问题
原始 GAN 中判别器要最小化如下损失函数,尽可能把真实样本分为正例,生成样本分为负例:
− E x ∼ P r [ log D ( x ) ] − E x ∼ P g [ log ( 1 − D ( x ) ) ] -\mathbb{E}_{x \sim P_r}[\log D(x)]-\mathbb{E}_{x \sim P_g}[\log (1-D(x))] −Ex∼Pr[logD(x)]−Ex∼Pg[log(1−D(x))]
一句话概括:判别器越好,生成器梯度消失越严重。
在生成器 G 固定参数时最优的判别器 D 应该是什么,对于一个具体样本 x x x 它对公式 1 损失函数的贡献是
− P r ( x ) log D ( x ) − P g ( x ) log [ 1 − D ( x ) ] -P_r(x) \log D(x)-P_g(x) \log [1-D(x)] −Pr(x)logD(x)−Pg(x)log[1−D(x)]
− P r ( x ) D ( x ) + P g ( x ) 1 − D ( x ) = 0 -\frac{P_r(x)}{D(x)}+\frac{P_g(x)}{1-D(x)}=0 −D(x)Pr(x)+1−D(x)Pg(x)=0
D ∗ ( x ) = P r ( x ) P r ( x ) + P g ( x ) D^*(x)=\frac{P_r(x)}{P_r(x)+P_g(x)} D∗(x)=Pr(x)+Pg(x)Pr(x)
如果 P r ( x ) = 0 P_r(x)=0 Pr(x)=0且 P g ( x ) ≠ 0 P_g(x)\neq0 Pg(x)=0 最优判别器就应该非常自信地给出概率 0;如果 P r ( x ) = P g ( x ) P_r(x)=P_g(x) Pr(x)=Pg(x)
说明该样本是真是假的可能性刚好一半一半,此时最优判别器也应该给出概率 0.5。
GAN 训练有一个 trick,就是别把判别器训练得太好,否则在实验中生成器会完全学不动(loss 降不下去),为了探究背后的原因,我们就可以看看在极端情况 —— 判别器最优时,生成器的损失函数变成什么。给公式 2 加上一个不依赖于生成器的项,使之变成
D ∗ ( x ) D^*(x) D∗(x) 带入 公式1 得到
E x ∼ P r log P r ( x ) 1 2 [ P r ( x ) + P g ( x ) ] + E x ∼ P g log P g ( x ) 1 2 [ P r ( x ) + P g ( x ) ] − 2 log 2 \mathbb{E}_{x \sim P_r} \log \frac{P_r(x)}{\frac{1}{2}\left[P_r(x)+P_g(x)\right]}+\mathbb{E}_{x \sim P_g} \log \frac{P_g(x)}{\frac{1}{2}\left[P_r(x)+P_g(x)\right]}-2 \log 2 Ex∼Prlog21[Pr(x)+Pg(x)]Pr(x)+Ex∼Pglog21[Pr(x)+Pg(x)]Pg(x)−2log2
K L ( P 1 ∥ P 2 ) = E x ∼ P 1 log P 1 P 2 J S ( P 1 ∥ P 2 ) = 1 2 K L ( P 1 ∥ P 1 + P 2 2 ) + 1 2 K L ( P 2 ∥ P 1 + P 2 2 ) \begin{aligned} & K L\left(P_1 \| P_2\right)=\mathbb{E}_{x \sim P_1} \log \frac{P_1}{P_2} \\ & J S\left(P_1 \| P_2\right)=\frac{1}{2} K L\left(P_1 \| \frac{P_1+P_2}{2}\right)+\frac{1}{2} K L\left(P_2 \| \frac{P_1+P_2}{2}\right) \end{aligned} KL(P1∥P2)=Ex∼P1logP2P1JS(P1∥P2)=21KL(P1∥2P1+P2)+21KL(P2∥2P1+P2)
2 J S ( P r ∥ P g ) − 2 log 2 2 J S\left(P_r \| P_g\right)-2 \log 2 2JS(Pr∥Pg)−2log2
key point
在最优判别器下,我们可以把原始GAN定义的生成器loss等价变换为最小化真实分布 P r P_r Pr 与生成分布 P g P_g Pg 之间的JS散度。我们越训练判别器,它就越接近最优。 最小化生成器的 loss 也就会越近似于最小化$ P_r$ 和 P g P_g Pg 之间的JS 散度。
问题就出在这个 JS 散度上。我们会希望如果两个分布之间越接近它们的 JS 散度越小,我们通过优化 JS 散度就能将 P g P_g Pg "拉向" P r P_r Pr, ,最终以假乱真。这个希望在两个分布有所重叠的时候是成立的,但是如果两个分布完全没有重叠的部分,或者它们重叠的部分可忽略(下面解释什么叫可忽略),它们的 JS 散度是多少呢? 答案是log2,因为对于任意一个 x 只有四种可能:
P 1 ( x ) = 0 且 P 2 ( x ) = 0 P 1 ( x ) ≠ 0 且 P 2 ( x ) ≠ 0 P 1 ( x ) = 0 且 P 2 ( x ) ≠ 0 P 1 ( x ) ≠ 0 且 P 2 ( x ) = 0 \begin{aligned} & P_1(x)=0 \text { 且 } P_2(x)=0 \\ & P_1(x) \neq 0 \text { 且 } P_2(x) \neq 0 \\ & P_1(x)=0 \text { 且 } P_2(x) \neq 0 \\ & P_1(x) \neq 0 \text { 且 } P_2(x)=0 \end{aligned} P1(x)=0 且 P2(x)=0P1(x)=0 且 P2(x)=0P1(x)=0 且 P2(x)=0P1(x)=0 且 P2(x)=0
- 第一种对计算 JS 散度无贡献
- 第二种情况由于重叠部分可忽略所以贡献也为 0
- 第三种情况对公式 7 右边第一个项的贡献 log P 2 1 2 ( P 2 + 0 ) = log 2 \log \frac{P_2}{\frac{1}{2}\left(P_2+0\right)}=\log 2 log21(P2+0)P2=log2
- 第四种情况 J S ( P 1 ∥ P 2 ) = log 2 J S\left(P_1 \| P_2\right)=\log 2 JS(P1∥P2)=log2
即无论 P r P_r Pr 跟 P g P_g Pg 是远在天边,还是近在眼前,只要它们俩没有一点重叠或者重叠部分可忽略,JS 散度就固定是常数log2, 而这对于梯度下降方法意味着 —— 梯度为 0.此时对于最优判别器来说,生成器肯定是得不到一丁点梯度信息的;即使对于接近最优的判别器来说,生成器也有很大机会面临梯度消失的问题。
Manifold A topological space that locally resembles Euclidean space near each point when this Euclidean space is of dimension n n n ,the manifold is referred as manifold.
- 支撑集(support)其实就是函数的非零部分子集,比如 ReLU 函数的支撑集就是(0,+∞),一个概率分布的支撑集就是所有概率密度非零部分的集合。
- 流形(manifold)是高维空间中曲线、曲面概念的拓广,我们可以在低维上直观理解这个概念,比如我们说三维空间中的一个曲面是一个二维流形,因为它的本质维度(intrinsic dimension)只有 2,一个点在这个二维流形上移动只有两个方向的自由度。同理,三维空间或者二维空间中的一条曲线都是一个一维流形。
P r Pr Pr 已发现它们集中在较低维流形中。这实际上是流形学习的基本假设。想想现实世界的图像,一旦主题或所包含的对象固定,图像就有很多限制可以遵循,例如狗应该有两只耳朵和一条尾巴,摩天大楼应该有笔直而高大的身体,等等。这些限制使图像无法具有高维自由形式。
P g P_g Pg 也存在于低维流形中。每当生成器被要求提供更大的图像(例如 64x64),给定小尺寸(例如 100),噪声变量输入 z z z 这4096个像素的颜色分布是由100维的小随机数向量定义的,很难填满整个高维空间。
P r P_r Pr 和 P g P_g Pg 不重叠或重叠部分可忽略的可能性有多大?不严谨的答案是:非常大。
both P r P_r Pr and p g p_g pg 处于低维流形中,他们几乎不会相交。(wgan 前面一篇理论证明)
GAN 中的生成器一般是从某个低维(比如 100 维)的随机分布中采样出一个编码向量 z z z,再经过一个神经网络生成出一个高维样本(比如 64x64 的图片就有 4096 维)。当生成器的参数固定时,生成样本的概率分布虽然是定义在 4096 维的空间上,但它本身所有可能产生的变化已经被那个 100 维的随机分布限定了,其本质维度就是 100,再考虑到神经网络带来的映射降维,最终可能比 100 还小,所以生成样本分布的支撑集就在 4096 维空间中构成一个最多 100 维的低维流形,“撑不满” 整个高维空间。
在这里插入图片描述
我们就得到了 WGAN 前作中关于生成器梯度消失的第一个论证:在(近似)最优判别器下,最小化生成器的 loss 等价于最小化 P r P_r Pr 与 P g P_g Pg 之间的JS散度,而由于 P r P_r Pr 与 P g P_g Pg 几乎不可能有不可忽略的重叠,所以无论它们相距多远 JS 散度都是常数log2,最终导致生成器的梯度(近似)为 0,梯度消失。
原始 GAN 不稳定的原因就彻底清楚了:判别器训练得太好,生成器梯度消失,生成器 loss 降不下去;判别器训练得不好,生成器梯度不准,四处乱跑。只有判别器训练得不好不坏才行,但是这个火候又很难把握,甚至在同一轮训练的前后不同阶段这个火候都可能不一样,所以 GAN 才那么难训练。
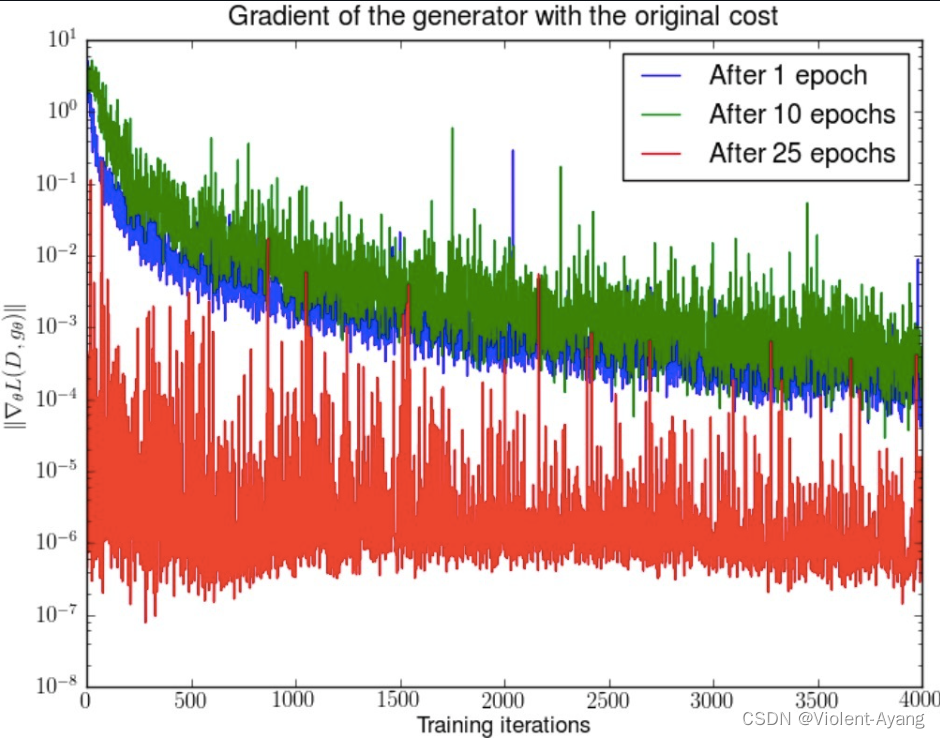
第二种原始 GAN 形式的问题 “the - log D trick”
一句话概括:最小化第二种生成器 loss 函数,会等价于最小化一个不合理的距离衡量,导致两个问题,一是梯度不稳定,二是 **Mode collapse 即多样性不足。**WGAN 前作又是从两个角度进行了论证
上文推导已经得到在最优判别器 D ∗ D^* D∗ 下
E x ∼ P r [ log D ∗ ( x ) ] + E x ∼ P g [ log ( 1 − D ∗ ( x ) ) ] = 2 J S ( P r ∥ P g ) − 2 log 2 \mathbb{E}_{x \sim P_r}\left[\log D^*(x)\right]+\mathbb{E}_{x \sim P_g}\left[\log \left(1-D^*(x)\right)\right]=2 J S\left(P_r \| P_g\right)-2 \log 2 Ex∼Pr[logD∗(x)]+Ex∼Pg[log(1−D∗(x))]=2JS(Pr∥Pg)−2log2
K L ( P g ∥ P r ) = E x ∼ P g [ log P g ( x ) P r ( x ) ] = E x ∼ P g [ log P g ( x ) / ( P r ( x ) + P g ( x ) ) P r ( x ) / ( P r ( x ) + P g ( x ) ) ] = E x ∼ P g [ log 1 − D ∗ ( x ) D ∗ ( x ) ] = E x ∼ P g log [ 1 − D ∗ ( x ) ] − E x ∼ P g log D ∗ ( x ) \begin{aligned} K L\left(P_g \| P_r\right) & =\mathbb{E}_{x \sim P_g}\left[\log \frac{P_g(x)}{P_r(x)}\right] \\ & =\mathbb{E}_{x \sim P_g}\left[\log \frac{P_g(x) /\left(P_r(x)+P_g(x)\right)}{P_r(x) /\left(P_r(x)+P_g(x)\right)}\right] \\ & =\mathbb{E}_{x \sim P_g}\left[\log \frac{1-D^*(x)}{D^*(x)}\right] \\ & =\mathbb{E}_{x \sim P_g} \log \left[1-D^*(x)\right]-\mathbb{E}_{x \sim P_g} \log D^*(x) \end{aligned} KL(Pg∥Pr)=Ex∼Pg[logPr(x)Pg(x)]=Ex∼Pg[logPr(x)/(Pr(x)+Pg(x))Pg(x)/(Pr(x)+Pg(x))]=Ex∼Pg[logD∗(x)1−D∗(x)]=Ex∼Pglog[1−D∗(x)]−Ex∼PglogD∗(x)
E x ∼ P g [ − log D ∗ ( x ) ] = K L ( P g ∥ P r ) − E x ∼ P g log [ 1 − D ∗ ( x ) ] = K L ( P g ∥ P r ) − 2 J S ( P r ∥ P g ) + 2 log 2 + E x ∼ P r [ log D ∗ ( x ) ] \begin{aligned} \mathbb{E}_{x \sim P_g}\left[-\log D^*(x)\right] & =K L\left(P_g \| P_r\right)-\mathbb{E}_{x \sim P_g} \log \left[1-D^*(x)\right] \\ & =K L\left(P_g \| P_r\right)-2 J S\left(P_r \| P_g\right)+2 \log 2+\mathbb{E}_{x \sim P_r}\left[\log D^*(x)\right] \end{aligned} Ex∼Pg[−logD∗(x)]=KL(Pg∥Pr)−Ex∼Pglog[1−D∗(x)]=KL(Pg∥Pr)−2JS(Pr∥Pg)+2log2+Ex∼Pr[logD∗(x)]
注意上式最后两项不依赖于生成器 G G G ,最终得到最小化公式 3 等价于最小化 K L ( P g ∥ P r ) − 2 J S ( P r ∥ P g ) K L\left(P_g \| P_r\right)-2 J S\left(P_r \| P_g\right) KL(Pg∥Pr)−2JS(Pr∥Pg)
这个等价最小化目标存在两个严重的问题。第一是它同时要最小化生成分布与真实分布的 KL 散度,却又要最大化两者的 JS 散度,一个要拉近,一个却要推远!这在直观上非常荒谬,在数值上则会导致梯度不稳定,这是后面那个 JS 散度项的毛病。
第二,即便是前面那个正常的 KL 散度项也有毛病。因为 KL 散度不是一个对称的衡量 K L ( P g ∥ P r ) K L\left(P_g \| P_r\right) KL(Pg∥Pr) 与 K L ( P r ∥ P g ) K L\left(P_r \| P_g\right) KL(Pr∥Pg) 是有差别的。
Wasserstein 距离的优越性质
W ( P r , P g ) = inf γ ∼ Π ( P r , P g ) E ( x , y ) ∼ γ [ ∥ x − y ∥ ] W\left(P_r, P_g\right)=\inf _{\gamma \sim \Pi\left(P_r, P_g\right)} \mathbb{E}_{(x, y) \sim \gamma}[\|x-y\|] W(Pr,Pg)=γ∼Π(Pr,Pg)infE(x,y)∼γ[∥x−y∥]
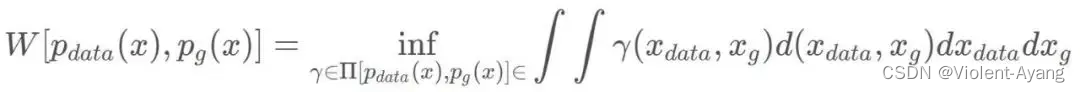
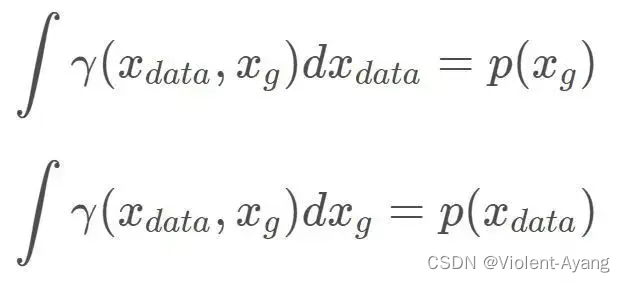

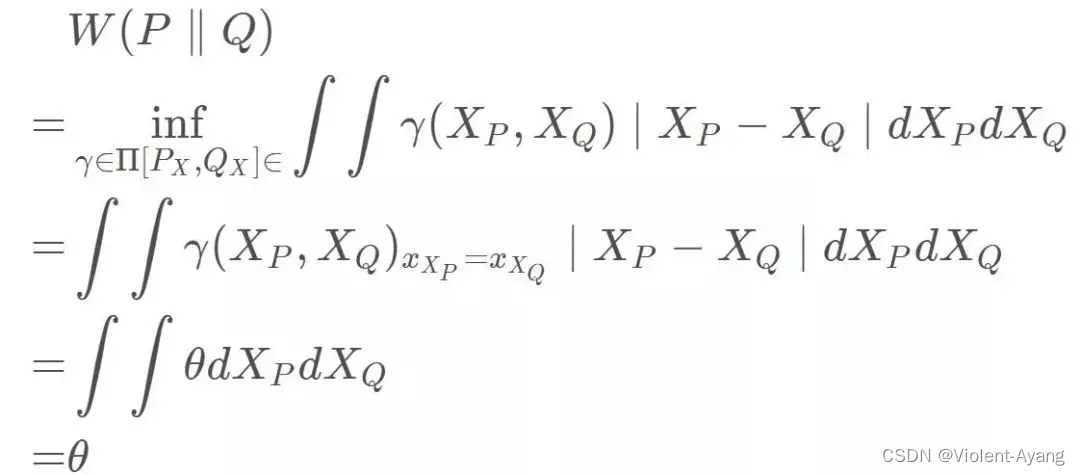
可以看出 Wasserstein 距离处处连续,而且几乎处处可导,数学性质非常好,能够在两个分布没有重叠部分的时候,依旧给出合理的距离度量。对于离散概率分布,Wasserstein 距离也被描述性地称为推土机距离 (EMD)。 如果我们将分布想象为一定量地球的不同堆,那么 EMD 就是将一个堆转换为另一堆所需的最小总工作量。
解释如下: Π ( P r , P g ) \Pi\left(P_r, P_g\right) Π(Pr,Pg) 是 P r P_r Pr 和 P g P_g Pg 组合起来的所有可能的联合分布的集合,反过来说, Π ( P r , P g ) \Pi\left(P_r, P_g\right) Π(Pr,Pg) 中每一个分布的边缘分布都是 P r P_r Pr 和 P g P_g Pg 。对于每一个可能的联合分布 γ \gamma γ 而言,可以从 中采样 ( x , y ) ∼ γ (x, y) \sim \gamma (x,y)∼γ 得到一个真实样本 x x x 和一个生成样本 y y y ,并算出这对样本的距离 ∥ x − y ∥ \|x-y\| ∥x−y∥ ,所 以可以计算该联合分布 γ \gamma γ 下样本对距离的期望值 E ( x , y ) ∼ γ [ ∥ x − y ∥ ] \mathbb{E}_{(x, y) \sim \gamma}[\|x-y\|] E(x,y)∼γ[∥x−y∥] 。在所有可能的联合分布中 够对这个期望值取到的下界inf in γ ∼ ( P r , P g ) E ( x , y ) ∼ γ [ ∥ x − y ∥ ] \operatorname{in}_{\gamma \sim\left(P_r, P_g\right)} \mathbb{E}_{(x, y) \sim \gamma}[\|x-y\|] inγ∼(Pr,Pg)E(x,y)∼γ[∥x−y∥] ,就定义为 Wasserstein 距离。
直观上可以把 E ( x , y ) ∼ γ [ ∥ x − y ∥ ] \mathbb{E}_{(x, y) \sim \gamma}[\|x-y\|] E(x,y)∼γ[∥x−y∥] 理解为在 γ \gamma γ 这个 “路径规划" 下把 P r P_r Pr 这堆 “沙土" 挪到 P g P_g Pg “位置” 所需的 “消耗”, 而 W ( P r , P g ) W\left(P_r, P_g\right) W(Pr,Pg) 就是 “最优路径规划" 下的 “最小消耗”,所以才 叫 Earth-Mover (推土机 ) 距离。
Wasserstein 距离相比 KL 散度、JS 散度的优越性在于,即便两个分布没有重叠,Wasserstein 距离仍然能够反映它们的远近。WGAN 本作通过简单的例子展示了这一点。考虑如下二维空间中 的两个分布 P 1 P_1 P1 和 P 2 , P 1 P_2 , P_1 P2,P1 在线段 A B \mathrm{AB} AB 上均匀分布, P 2 P_2 P2 在线段 C D \mathrm{CD} CD 上均匀分布,通过控制参数 θ \theta θ 可以控制着两个分布的距离远近。
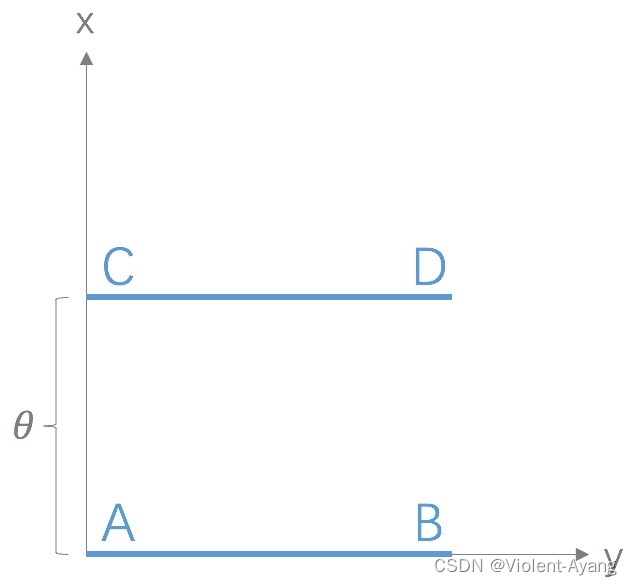
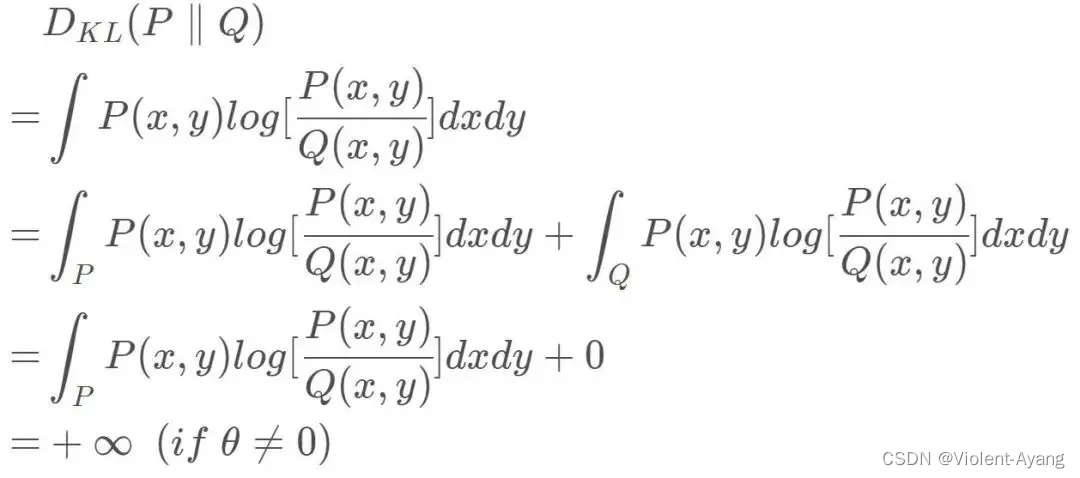
K L ( P 1 ∥ P 2 ) = K L ( P 1 ∣ ∣ P 2 ) = { + ∞ if θ ≠ 0 0 if θ = 0 (突变) J S ( P 1 ∥ P 2 ) = { log 2 if θ ≠ 0 0 if θ − 0 (突变 ) W ( P 0 , P 1 ) = ∣ θ ∣ (平滑 ) \begin{aligned} & K L\left(P_1 \| P_2\right)=K L\left(P_1|| P_2\right)=\left\{\begin{array}{ll} +\infty & \text { if } \theta \neq 0 \\ 0 & \text { if } \theta=0 \end{array}\right. \text { (突变) } \\ & J S\left(P_1 \| P_2\right)=\left\{\begin{array}{ll} \log 2 & \text { if } \theta \neq 0 \\ 0 & \text { if } \theta-0 \end{array}\right. \text { (突变 ) } \\ & W\left(P_0, P_1\right)=|\theta| \text { (平滑 ) } \end{aligned} KL(P1∥P2)=KL(P1∣∣P2)={+∞0 if θ=0 if θ=0 (突变) JS(P1∥P2)={log20 if θ=0 if θ−0 (突变 ) W(P0,P1)=∣θ∣ (平滑 )
第四部分:从 Wasserstein 距离到 WGAN
EMD ( P r , P θ ) = inf γ ∈ Π ∑ x , y ∥ x − y ∥ γ ( x , y ) = inf γ ∈ Π E ( x , y ) ∼ γ ∥ x − y ∥ \operatorname{EMD}\left(P_r, P_\theta\right)=\inf _{\gamma \in \Pi} \sum_{x, y}\|x-y\| \gamma(x, y)=\inf _{\gamma \in \Pi} \mathbb{E}_{(x, y) \sim \gamma}\|x-y\| EMD(Pr,Pθ)=γ∈Πinfx,y∑∥x−y∥γ(x,y)=γ∈ΠinfE(x,y)∼γ∥x−y∥
It is intractable to exhaust all the possible joint distributions in Π ( p r , p g ) \Pi\left(p_r, p_g\right) Π(pr,pg) to compute inf γ ∼ Π ( p r , p g ) \inf _{\gamma \sim \Pi\left(p_r, p_g\right)} infγ∼Π(pr,pg) Thus the authors proposed a smart transformation of the formula based on the KantorovichRubinstein duality to: 作者提出了基于 Kantorovich-Rubinstein 对偶性的公式的巧妙转换:
W ( p r , p g ) = 1 K sup ∥ f ∥ L ≤ K E x ∼ p r [ f ( x ) ] − E x ∼ p g [ f ( x ) ] W\left(p_r, p_g\right)=\frac{1}{K} \sup _{\|f\| L \leq K} \mathbb{E}_{x \sim p_r}[f(x)]-\mathbb{E}_{x \sim p_g}[f(x)] W(pr,pg)=K1∥f∥L≤KsupEx∼pr[f(x)]−Ex∼pg[f(x)]
首先需要介绍一个概念——Lipschitz 连续。它其实就是在一个连续函数 f f f 上面额外施加了一个限 制,要求存在一个常数 K ≥ 0 K \geq 0 K≥0 使得定义域内的任意两个元素 x 1 x_1 x1 和 x 2 x_2 x2 都满足
∣ f ( x 1 ) − f ( x 2 ) ∣ ≤ K ∣ x 1 − x 2 ∣ \left|f\left(x_1\right)-f\left(x_2\right)\right| \leq K\left|x_1-x_2\right| ∣f(x1)−f(x2)∣≤K∣x1−x2∣
此时称函数 f f f 的 Lipschitz 常数为 K K K 。
上述公式 的意思就是在要求函数 f f f 的 Lipschitz 常数 ∣ f ∥ L \mid f \|_L ∣f∥L 不超过 K K K 的条件下,对所有可能满足 件的 f f f 取到趻 数 w w w 来定义一系列可能的函数 f w f_w fw ,此时求解公式 可以近似变成求解如下形式
K ⋅ W ( P r , P g ) ≈ max w : ∣ f w ∣ L ≤ K E x ∼ P r [ f w ( x ) ] − E x ∼ P g [ f w ( x ) ] K \cdot W\left(P_r, P_g\right) \approx \max _{w:\left|f_w\right|_L \leq K} \mathbb{E}_{x \sim P_r}\left[f_w(x)\right]-\mathbb{E}_{x \sim P_g}\left[f_w(x)\right] K⋅W(Pr,Pg)≈w:∣fw∣L≤KmaxEx∼Pr[fw(x)]−Ex∼Pg[fw(x)]
W ( p r , p θ ) = inf γ ∈ π ∬ ∥ x − y ∥ γ ( x , y ) d x d y = inf γ ∈ π E x , y ∼ γ [ ∥ x − y ∥ ] . W\left(p_r, p_\theta\right)=\inf _{\gamma \in \pi} \iint\|x-y\| \gamma(x, y) \mathrm{d} x \mathrm{~d} y=\inf _{\gamma \in \pi} \mathbb{E}_{x, y \sim \gamma}[\|x-y\|] . W(pr,pθ)=γ∈πinf∬∥x−y∥γ(x,y)dx dy=γ∈πinfEx,y∼γ[∥x−y∥].
W ( p r , p θ ) = inf γ ∈ π E x , y ∼ γ [ ∥ x − y ∥ ] = inf γ E x , y ∼ γ [ ∥ x − y ∥ + sup f E s ∼ p r [ f ( s ) ] − E t ∼ p θ [ f ( t ) ] − ( f ( x ) − f ( y ) ) ] ⏟ = { 0 , if γ ∈ π + ∞ else = inf γ sup f E x , y ∼ γ [ ∥ x − y ∥ + E s ∼ p r [ f ( s ) ] − E t ∼ p θ [ f ( t ) ] − ( f ( x ) − f ( y ) ) ] \begin{aligned} W\left(p_r, p_\theta\right) & =\inf _{\gamma \in \pi} \mathbb{E}_{x, y \sim \gamma}[\|x-y\|] \\ & =\inf _\gamma \mathbb{E}_{x, y \sim \gamma}[\|x-y\|+\underbrace{\left.\sup _f \mathbb{E}_{s \sim p_r}[f(s)]-\mathbb{E}_{t \sim p_\theta}[f(t)]-(f(x)-f(y))\right]} \\ & =\left\{\begin{array}{c} 0, \text { if } \gamma \in \pi \\ +\infty \text { else } \end{array}\right. \\ & =\inf _\gamma \sup _f \mathbb{E}_{x, y \sim \gamma}\left[\|x-y\|+\mathbb{E}_{s \sim p_r}[f(s)]-\mathbb{E}_{t \sim p_\theta}[f(t)]-(f(x)-f(y))\right] \end{aligned} W(pr,pθ)=γ∈πinfEx,y∼γ[∥x−y∥]=γinfEx,y∼γ[∥x−y∥+ fsupEs∼pr[f(s)]−Et∼pθ[f(t)]−(f(x)−f(y))]={0, if γ∈π+∞ else =γinffsupEx,y∼γ[∥x−y∥+Es∼pr[f(s)]−Et∼pθ[f(t)]−(f(x)−f(y))]
sup f inf γ E x , y ∼ γ [ ∥ x − y ∥ + E s ∼ p r [ f ( s ) ] − E t ∼ p θ [ f ( t ) ] − ( f ( x ) − f ( y ) ) ] = sup f E s ∼ p r [ f ( s ) ] − E t ∼ p θ [ f ( t ) ] + inf γ E x , y ∼ γ [ ∥ x − y ∥ − ( f ( x ) − f ( y ) ) ] ⏟ γ = { 0 , if ∥ f ∥ L ≤ 1 − ∞ else \begin{array}{r} \sup _f \inf _\gamma \mathbb{E}_{x, y \sim \gamma}\left[\|x-y\|+\mathbb{E}_{s \sim p_r}[f(s)]-\mathbb{E}_{t \sim p_\theta}[f(t)]-(f(x)-f(y))\right] \\ =\sup _f \mathbb{E}_{s \sim p_r}[f(s)]-\mathbb{E}_{t \sim p_\theta}[f(t)]+\underbrace{\inf _\gamma \mathbb{E}_{x, y \sim \gamma}[\|x-y\|-(f(x)-f(y))]}_\gamma \\ =\left\{\begin{array}{cc} 0, & \text { if }\|f\|_L \leq 1 \\ -\infty & \text { else } \end{array}\right. \end{array} supfinfγEx,y∼γ[∥x−y∥+Es∼pr[f(s)]−Et∼pθ[f(t)]−(f(x)−f(y))]=supfEs∼pr[f(s)]−Et∼pθ[f(t)]+γ γinfEx,y∼γ[∥x−y∥−(f(x)−f(y))]={0,−∞ if ∥f∥L≤1 else
W ( p r , p θ ) = sup f E s ∼ p r [ f ( s ) ] − E t ∼ p θ [ f ( t ) ] + inf γ E x , y ∼ γ [ ∥ x − y ∥ − ( f ( x ) − f ( y ) ) ] = sup ∥ f ∥ L ≤ 1 E s ∼ p r [ f ( s ) ] − E t ∼ p θ [ f ( t ) ] \begin{aligned} W\left(p_r, p_\theta\right) & =\sup _f \mathbb{E}_{s \sim p_r}[f(s)]-\mathbb{E}_{t \sim p_\theta}[f(t)]+\inf _\gamma \mathbb{E}_{x, y \sim \gamma}[\|x-y\|-(f(x)-f(y))] \\ & =\sup _{\|f\|_{L \leq 1}} \mathbb{E}_{s \sim p_r}[f(s)]-\mathbb{E}_{t \sim p_\theta}[f(t)] \end{aligned} W(pr,pθ)=fsupEs∼pr[f(s)]−Et∼pθ[f(t)]+γinfEx,y∼γ[∥x−y∥−(f(x)−f(y))]=∥f∥L≤1supEs∼pr[f(s)]−Et∼pθ[f(t)]
相关文章:
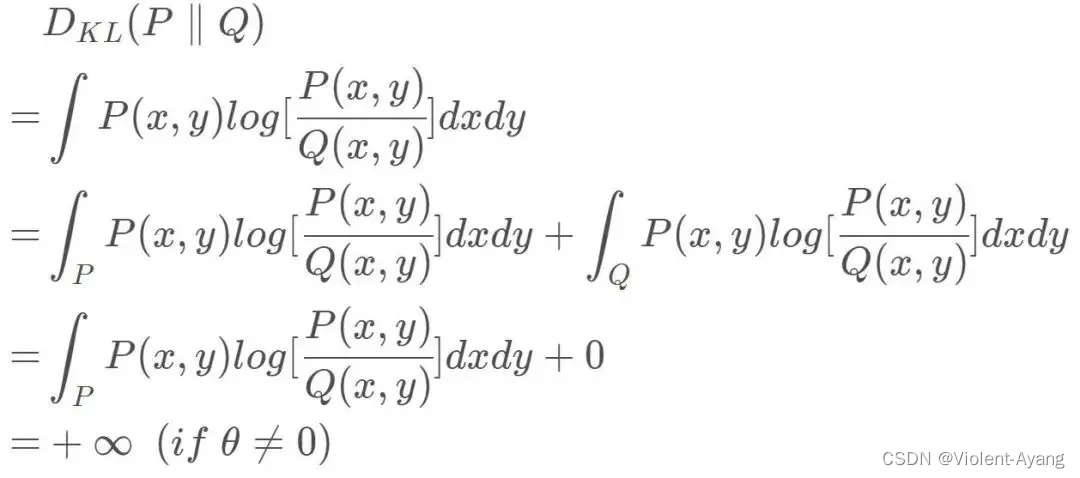
WGAN(Wassertein GAN)
WGAN E x ∼ P g [ log ( 1 − D ( x ) ) ] E x ∼ P g [ − log D ( x ) ] \begin{aligned} & \mathbb{E}_{x \sim P_g}[\log (1-D(x))] \\ & \mathbb{E}_{x \sim P_g}[-\log D(x)] \end{aligned} Ex∼Pg[log(1−D(x))]Ex∼Pg[−logD(x)] 原始 GAN …...
Maven基本使用
1. Maven前瞻 Maven官网:https://maven.apache.org/ Maven镜像:https://mvnrepository.com 1.1、Maven是什么 Maven是一个功能强大的项目管理和构建工具,可以帮助开发人员简化Java项目的构建过程。 在Maven中,使用一个名为 pom.…...

在Linux系统中配置GitHub的SSH公钥
在Linux系统中配置GitHub的SSH公钥,可以让您无需频繁输入密码即可与GitHub仓库进行交互,提高工作效率。以下是配置步骤: 第一步: 检查SSH密钥是否存在 首先,检查您的用户目录下的.ssh文件夹中是否已有SSH密钥。打开终端࿰…...

小酌消烦暑|人间正清欢
小暑是二十四节气之第十一个节气。暑,是炎热的意思,小暑为小热,还不十分热。小暑虽不是一年中最炎热的时节,但紧接着就是一年中最热的节气大暑,民间有"小暑大暑,上蒸下煮"之说。中国多地自小暑起…...

C语言结构体的相关知识
前言 从0开始记录我的学习历程,我会尽我所能,写出最最大白话的文章,希望能够帮到你,谢谢。 1.结构体类型的概念及定义 1.1、概念: 结构体是一种构造类型的数据结构, 是一种或多种基本类型或构造类型的数…...
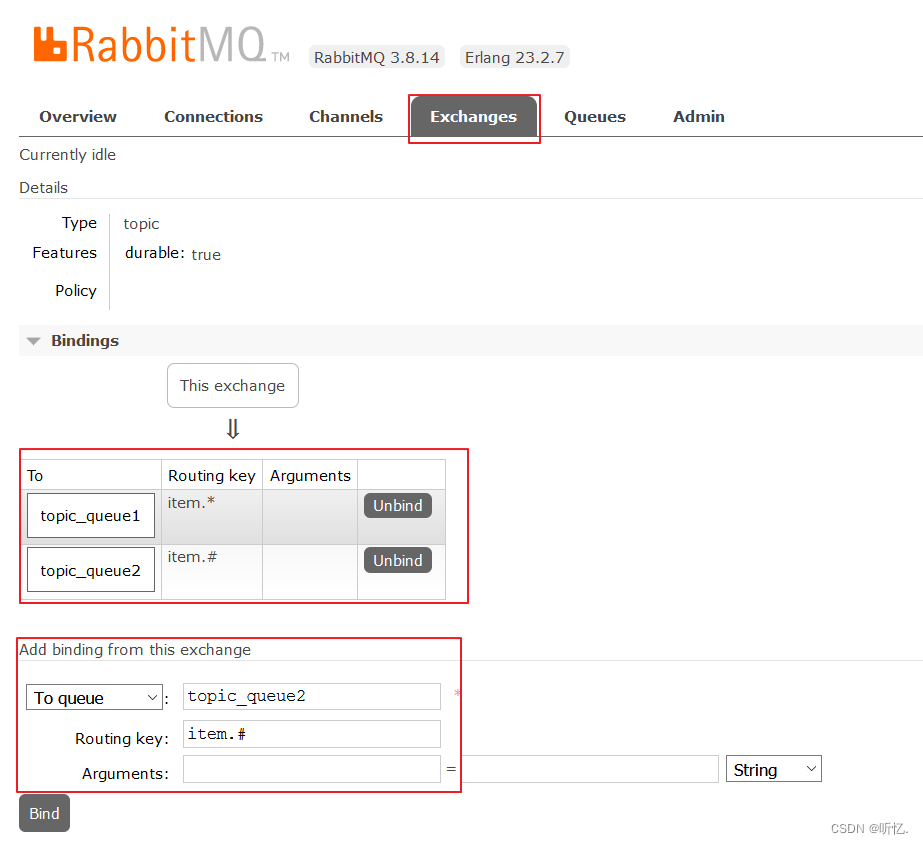
RabbitMQ入门教程(精细版二带图)
目录 六 RabbitMQ工作模式 6.1Hello World简单模式 6.1.1 什么是简单模式 6.1.2 RabbitMQ管理界面操作 6.1.3 生产者代码 6.1.4 消费者代码 6.2 Work queues工作队列模式 6.2.1 什么是工作队列模式 6.2.2 RabbitMQ管理界面操作 6.2.3 生产者代码 6.2.4 消费者代码 …...

IO、零拷贝、多路复用、connection、池化
目录 一、IO 模型 二、什么是网络IO 三、什么是零拷贝 四、多路复用 五、java程序、mysql JDBC connection关系 六、connection怎么操作事务 七 、java里面的池化技术 八、线程池7个核心参数 九、线程的状态 一、IO 模型 BIO :同步阻塞io,单线程 内存上下…...

Lua 错误处理
Lua 错误处理 Lua是一种轻量级的编程语言,广泛用于游戏开发、脚本编写和其他应用程序中。在编程过程中,错误处理是一个重要的方面,它可以帮助开发者创建更健壮和可靠的程序。本文将详细介绍Lua中的错误处理机制。 错误类型 在Lua中&#x…...

二刷力扣——单调栈
739. 每日温度 单调栈应该从栈底到栈顶 是递减的。 找下一个更大的 ,用递减单调栈,就可以确定在栈里面的每个比当前元素i小的元素,下一个更大的就是这个i,然后弹出并记录;然后当前元素i入栈,仍然满足递减…...

elementPlus-vue3-ts表格单选和双选实现方式
记录在vue3、ts、element-plus环境下表格单选和多选的实现方式 单选 html部分 <el-table...reftaskTableRefselect"selectClick"... ><el-table-column type"selection" width"50" />... </el-table>ts部分 const taskTabl…...

Linux系统中卸载GitLab
在Linux系统中卸载GitLab,主要可以通过包管理器(如apt、yum、rpm等)来实现,但具体步骤可能会因GitLab的安装方式(如使用包管理器安装、从源代码安装、使用Docker等)和Linux发行版的不同而有所差异。以下是一…...

基于STM32F407ZG的FreeRTOS移植
1.从FreeRTOS官网中下载源码 2、简单分析FreeRTOS源码目录结构 2.1、简单分析FreeRTOS源码根目录 (1)Demo:是官方为一些单片机移植FreeRTOS的例程 (2)License:许可信息 (3)Sourc…...

【IT领域新生必看】Java编程中的神奇对比:深入理解`equals`与`==`的区别
文章目录 引言什么是操作符?基本数据类型的比较示例: 引用类型的比较示例: 什么是equals方法?equals方法的默认实现示例: 重写equals方法示例: equals与的区别比较内容不同示例: 使用场景不同示…...

WEBHTTP
目录 理解HTTP协议请求流程 1 1 Web基础 2 Hosts文件 1 1 2网页与HTML 2 HTML概述 1 1 3静态网页与动态网页 1.2HTTP协议 1 2 1 HTTP协议概述 1 2 2 HTTP方法 HTTP支持几种不同的请求命令,这些命令被称为HTTP方法(HTTP method 表1一3 HTTP方法 表1&#…...

nodejs 获取客服端ip,以及获取ip一直都是127.0.0.1的问题
一、问题描述 在做登录日志的时候想要获取客户端的ip, 网上查了一下 通过 req.headers[x-forwarded-for] || req.connection.remoteAddress; 获取, 结果获取了之后不管是开发环境,还是生产环境获取到的一直都是 127.0.0.1,这是因为在配置N…...

微软与OpenAI/谷歌与三星的AI交易受欧盟重点关注
近日,欧盟委员会主管竞争事务的副主席玛格丽特维斯塔格(Margrethe Vestager)在一次演讲中透露,欧盟反垄断监管机构将就微软与OpenAI的合作,以及谷歌与三星达成的AI协议寻求更多第三方意见。这意味着微软与 OpenAI、谷歌与三星的 AI 交易及合作…...

微信小程序毕业设计-学生实习与就业管理系统项目开发实战(附源码+论文)
大家好!我是程序猿老A,感谢您阅读本文,欢迎一键三连哦。 💞当前专栏:微信小程序毕业设计 精彩专栏推荐👇🏻👇🏻👇🏻 🎀 Python毕业设计…...

spring boot 接口参数解密和返回值加密
spring boot 接口参数解密和返回值加密 开发背景简介安装配置yml 方式Bean 方式 试一下启动项目返回值加密参数解密body 参数解密param和form-data参数解密 总结 开发背景 虽然使用 HTTPS 已经可以基本保证传输数据的安全性,但是很多国企、医疗、股票项目等仍然要求…...

C语言自定义类型——联合体、枚举
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、联合体(一)、联合体的声明(二)、联合体的特点(三)、联合体大小的计算!&a…...

【trition-server】pytorch 文档:使用 Triton 提供 Torch-TensorRT 模型
Serving a Torch-TensorRT model with Triton pytorch 的官方文档: Serving a Torch-TensorRT model with Triton 在有关机器学习基础设施的讨论中,优化和部署是密不可分的。一旦完成网络级优化以获得最大性能,下一步就是部署它。 然而,提供这种优化模型也有其自身的一系列…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...
