集成学习(三)GBDT 梯度提升树
前面学习了:集成学习(二)Boosting-CSDN博客
梯度提升树:GBDT-Gradient Boosting Decision Tree
一、介绍
作为当代众多经典算法的基础,GBDT的求解过程可谓十分精妙,它不仅开创性地舍弃了使用原始标签进行训练的方式,同时还极大地简化了Boosting算法的运算流程,让Boosting算法本该非常复杂的运算流程变得清晰简洁。GBDT的数学流程非常简明、美丽,同时这一美丽的流程也是我们未来所有Boosting高级算法的数学基础。与任意Boosting算法一致,对GBDT我们需要回答如下问题:
- 损失函数
的表达式是什么?损失函数如何影响模型构建?
- 弱评估器
是什么,当下boosting算法使用的具体建树过程是什么?
- 综合集成结果
是什么?集成算法具体如何输出集成结果?
同时,还可能存在其他需要明确的问题,例如:
- 是加权求和吗?如果是,加权求和中的权重如何求解?
- 训练过程中,拟合的数据
与
分别是什么?
回顾Boosting算法的基本指导思想,我们来梳理梯度提升树回归算法的基本流程。虽然Boosting理论很早就被人提出,但1999年才是GBDT算法发展的高潮。1999年,有四篇论文横空出世:
《贪心函数估计:一种梯度提升机器》
Friedman, J. H. (February 1999). "Greedy Function Approximation: A Gradient Boosting Machine"《随机梯度提升》
Friedman, J. H. (March 1999). "Stochastic Gradient Boosting"《梯度下降式提升算法》
Mason, L.; Baxter, J.; Bartlett, P. L.; Frean, Marcus (1999). "Boosting Algorithms as Gradient Descent"《函数空间中的梯度下降式提升算法》
Mason, L.; Baxter, J.; Bartlett, P. L.; Frean, Marcus (May 1999). "Boosting Algorithms as Gradient Descent in Function Space"
GBDT算法是融合了上述4篇论文思想的集大成之作,为了保持一致,使用与前文不同的数学符号。
二、数学过程
假设现有数据集 ,含有形如的样本
个,
为任意样本的编号,单一样本的损失函数为
,其中
是
号样本在集成算法上的预测结果,整个算法的损失函数为
,且总损失等于全部样本的损失之和:
。同时,弱评估器为回归树 ,总共学习
轮。则GBDT回归的基本流程如下所示:
1、初始化数据迭代的起点
。sklearn当中,我们可以使用0、随机数或者任意算法的输出结果作为
,但在最初的论文中,Friedman定义了如下公式来计算
:

其中 为真实标签, C 为任意常数。以上式子表示,找出令
最小的常数 C 值,并输出最小的
作为
的值。需要注意的是,由于
是由全部样本的
计算出来的,因此所有样本的初始值都是
,不存在针对某一样本的单一初始值。
开始循环,for t in 1,2,3...T:
2、在现有数据集 N 中,抽样 M∗subsample 个样本,构成训练集
3、对任意一个样本,计算伪残差(pseudo-residuals)
,具体公式为:

不难发现,伪残差是一个样本的损失函数对该样本在集成算法上的预测值求导后取负的结果,并且在进行第次迭代、计算第
个伪残差时,我们使用的前
次迭代后输出的集成算法结果。在
时,所有伪残差计算中的
都等于初始
,在
时,每个样本上的
都是不同的取值。
4、求解出伪残差后,在数据集
上按照CART树规则建立一棵回归树
,训练时拟合的标签为样本的伪残差
。
5、将数据集
上所有的样本输入
进行预测,对每一个样本,得出预测结果
。在数学上我们可以证明,只要拟合对象是伪残差
,则
的值一定能让损失函数最快减小。
6、根据预测结果
迭代模型,具体来说:
![]()
假设输入的步长为,则
应该为:
![]()
对整个算法则有:
![]()
7、循环结束,输出 的值作为集成模型的输出值。
三、初始化 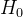 过程中的常数C是什么?
过程中的常数C是什么?
在最初的论文中,Friedman定义了如下公式来计算 :

其中 为真实标签, C 为任意常数。以上式子表示,找出令
最小的常数 C 值,并输出最小的
作为
的值。在刚观察这个式子时,大家可能很难理解 C 这个常数的作用,但这个式子实际上很简单。
首先,是损失函数,损失函数衡量两个自变量之间的差异,因此
衡量样本
的真实标签
与常数C之间的差异,因此
是所有样本的真实标签与常数C之间的差异之和。现在我们要找到一个常数C,令所有样本的真实标签与常数C的差异之和最小,请问常数C是多少呢?这是一个典型的求极值问题,只需要对
求导,再令导数为0就可以解出令
最佳的C。假设
是squared_error,每个样本的平方误差,则有:

对上述式子求导,并令一阶导数等于0:

所以:

可知,当L是平方误差squared error时,令 最小的常数C就是真实标签的均值。因此,式子
的本质其实是求解
时的损失函数,并以此损失函数作为
的值。当然,如果我们选择了其他的损失函数,我们就需要以其他方式(甚至梯度下降)进行求解, C 的值可能也就不再是均值了。
四、为什么拟合伪残差可以令损失函数最快地减小
从直觉上来看,拟合伪残差可以降低与
之间的差异,从而降低整体损失函数的值,但这个行为在数学上真的可行吗?毕竟,GBDT可以使用任意可微函数作为损失函数,不同损失函数求导后的结果即便与残差相似,也未必能代替真正的残差的效果。因此,不仅在直觉上需要理解拟合伪残差的作用,我们还需要从数学上证明:只要拟合对象是伪残差
,则弱评估器的输出值
一定是让损失函数减小最快的值。
我们可以对损失函数进行泰勒展开。对单一样本而言,我们有损失函数,其中
是已知的常数,因此损失函数可以被看做是只有
一个自变量的函数,从而简写为
。
根据一阶泰勒展开,已知:

该式子中 是常数,因此第一部分
也是一个常数。同时,第二部分由导数和
组成,其中导数就是梯度,可以写作
,所以式子可以化简为:
![]()
现在,如果要令 最小,
应该等于多少呢?回到我们最初的目标,找出令损失函数
最小的
值:

常数无法被最小化,因此继续化简:

现在, 是包含了所有样本梯度的向量,
是包含了所有样本在
上预测值的向量,两个向量对应位置元素相乘后求和,即表示为向量的内积,由尖括号 〈〉 表示。现在我们希望求解向量内积的最小值、并找出令向量内积最小的
的取值,那就必须先找出
的方向,再找出
的大小。
1、方向
的方向应该与
完全相反。向量的内积
,其中前两项为两个向量的模长, α 是两个向量的夹角大小。模长默认为整数,因此当且仅当两个向量的方向完全相反,即夹角大小为180度时, cos(α) 的值为-1,才能保证两个向量的内积最小。假设向量 a = [1,2],向量b是与a的方向完全相反的向量。假设a和b等长,那向量b就是[-1,-2]。因此,与
方向完全相反且等长的向量就是 ,
,
的方向也正是
的方向。


2、大小
对于向量a,除了[-1,-2]之外,还存在众多与其呈180度夹角、但大小不一致的向量,比如[-2,-4], [-0.5,-1],每一个都可以与向量a求得内积。并且我们会发现,当方向相反时,向量b中的元素绝对值越大,b的模长就越长,向量a与b的内积就越小。因此不难发现, 是一个理论上可以取到无穷小的值,那我们的 ft(x) 应该取什么大小呢?答案非常出乎意料:任何大小都无所谓。

回到我们的迭代公式:
![]()
![]()
无论 的大小是多少,我们都可以通过步长 η 对其进行调整,只要能够影响
,我们就可以影响损失迭代过程中的常数的大小。因此在数学上来说,
的大小可以是
的任意倍数,这一点在梯度下降中其实也是一样的。为了方便起见,同时为了与传统梯度下降过程一致,我们通常让
就等于一倍的
,但也有不少论文令
等于其他值的。在GBDT当中:

这就是我们让GBDT当中的弱评估器拟合伪残差/负梯度的根本原因。拟合负梯度其实为GBDT带来了非常多的特点:
首先,通过直接拟合负梯度,GBDT避免了从损失函数找“最优”的过程,即避免了上述证明中求解
的过程,从而大大地简化了计算。
其次,通过拟合负梯度,GBDT模拟了梯度下降的过程,由于结合了传统提升法Boosting与梯度下降,因此才被命名为梯度提升法(Gradient Boosting)。这个过程后来被称为函数空间上的梯度下降(Gradient Descent in Function Space),这是视角为Boosting算法的发展奠定了重要的基础。
最后,最重要的一点是,通过让弱评估器拟合负梯度,弱评估器上的结果可以直接影响损失函数、保证损失函数的降低,从而指向Boosting算法的根本目标:降低偏差。这一过程避免了许多在其他算法中需要详细讨论的问题:例如,每个弱评估器的权重 ϕ 是多少,以及弱评估器的置信度如何。
在AdaBoost算法当中,损失函数是“间接”影响弱评估器的建立,因此有的弱评估器能够降低损失函数,而有的弱评估器不能降低损失函数,因此要在求和之前,需要先求解弱评估器的置信度,然后再给与置信度高的评估器更高的权重,权重 ϕ 存在的根本意义是为了调节单一弱评估器对 ϕ 的贡献程度。但在GBDT当中,由于所有的弱评估器都是能够降低损失函数的,只不过降低的程度不同,因此就不再需要置信度/贡献度的衡量,因此就不再需要权重 ϕ 。
五、遗留问题
有些细节性的东西本文还没有讲到,比如:
- 叶子结点如何取值?
- 其他损失函数下怎么推导?
- ...
详见下面《集成学习(四)DT、GBDT 公式推导》,注意:这两篇文章的符号不一样!!
接下来学习:
相关文章:
集成学习(三)GBDT 梯度提升树
前面学习了:集成学习(二)Boosting-CSDN博客 梯度提升树:GBDT-Gradient Boosting Decision Tree 一、介绍 作为当代众多经典算法的基础,GBDT的求解过程可谓十分精妙,它不仅开创性地舍弃了使用原始标签进行…...

后端工作之一:CrapApi —— API接口管理系统部署
一个API接口的网络请求都有这些基本元素构成: API接口大多数是由后端编写,前端开发人员进行请求调用 就是一个网络请求的流程。 API(Application Programming Interface)接口是现代软件开发中不可或缺的一部分。它们提供了一种…...
的实时驱动更换)
20240706 xenomai系统中网口(m2/minipcie I210网卡)的实时驱动更换
lspci 查看网口 查看网口驱动 1 ubuntu 查看网口驱动 在Ubuntu中,您可以使用lshw命令来查看网络接口的驱动信息。如果lshw没有安装,您可以通过执行以下命令来安装它: sudo apt-get update sudo apt-get install lshw 安装完成后ÿ…...

模型训练之数据集
我们知道人工智能的四大要素:数据、算法、算力、场景。我们训练模型离不开数据 目标 一、数据集划分 定义 数据集:训练集是一组训练数据。 样本:一组数据中一个数据 特征:反映样本在某方面的表现、属性或性质事项 训练集&#…...

【TB作品】数码管独立按键密码锁,ATMEGA16单片机,Proteus仿真 atmega16数码管独立按键密码锁
文章目录 基于ATmega16的数码管独立按键密码锁设计实验报告实验背景硬件介绍主要元器件电路连接 设计原理硬件设计软件设计 程序原理延时函数独立按键检测密码显示主函数 资源代码 基于ATmega16的数码管独立按键密码锁设计实验报告 实验背景 本实验旨在设计并实现一个基于ATm…...
数据库主从复制
目录 一.主从复制架构 二.主从复制原理 三.实现主从复制配置 1.新建主从复制 2.实战遇到问题 3.复制错误解决方法 4.级联 主从复制 5.半同步复制 MySQL数据库的主从复制(Master-Slave Replication)是一种常见的数据库复制架构,用于提…...

昇思25天学习打卡营第13天|BERT
一、简介: BERT全称是来自变换器的双向编码器表征量(Bidirectional Encoder Representations from Transformers),它是Google于2018年末开发并发布的一种新型语言模型。与BERT模型相似的预训练语言模型例如问答、命名实体识别、自…...

跨平台书签管理器 - Raindrop
传统的浏览器书签功能虽然方便,但在管理和分类上存在诸多局限。今天,我要向大家推荐一款功能强大的跨平台书签管理-Raindrop https://raindrop.io/ 📢 主要功能: 智能分类和标签管理 强大的搜索功能 跨平台支持 分享与协作 卡片式…...
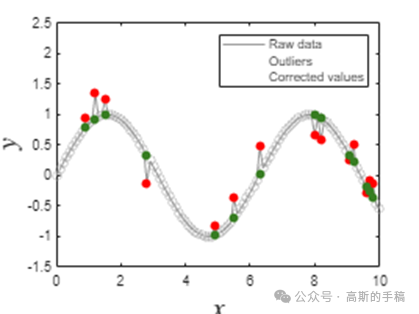
均匀采样信号的鲁棒Savistky-Golay滤波(MATLAB)
S-G滤波器又称S-G卷积平滑器,它是一种特殊的低通滤波器,用来平滑噪声数据。该滤波器被广泛地运用于信号去噪,采用在时域内基于多项式最小二乘法及窗口移动实现最佳拟合的方法。与通常的滤波器要经过时域-频域-时域变换…...

c++ 可以再头文件种直接给成员变量赋值吗
在C中,你通常不能在头文件中直接给类的成员变量赋值,因为这会导致每个包含该头文件的源文件中都尝试进行赋值,从而引发多重定义错误。然而,你可以在类的构造函数中初始化成员变量,或者在类声明中使用初始化列表或默认成…...

47.HOOK引擎优化支持CALL与JMP位置做HOOK
免责声明:内容仅供学习参考,请合法利用知识,禁止进行违法犯罪活动! 上一个内容:46.修复HOOK对代码造成的破坏 以 46.修复HOOK对代码造成的破坏 它的代码为基础进行修改 优化的是让引擎支持从短跳JMP(E9&…...

liunx上修改Firefox版本号
在Linux上修改Firefox的版本号并不直接推荐也不鼓励,因为这可能会影响到浏览器的安全性、兼容性和自动更新功能。但如果你因为某些特殊测试场景确实需要修改其显示的版本号(请注意,这样做可能会引发不可预料的问题),可…...

bug——多重定义
bug——多重定义 你的问题是在C代码中遇到了"reference to data is ambiguous"的错误。这个错误通常发生在你尝试引用一个具有多重定义的变量时。 在你的代码中,你定义了一个全局变量data,同时,C标准库中也有一个名为data的函数模板…...
与最大值(Xmx)设置为相同的配置,可以防止JVM在运行过程中根据需要动态调整堆内存大小)
将堆内存的最小值(Xms)与最大值(Xmx)设置为相同的配置,可以防止JVM在运行过程中根据需要动态调整堆内存大小
将堆内存的最小值(Xms)与最大值(Xmx)设置为相同的配置,可以防止JVM在运行过程中根据需要动态调整堆内存大小,从而避免因内存分配策略变化引起的性能波动,也就是所谓的"内存震荡"&…...

安装 tesseract
安装 tesseract 1. Ubuntu-24.04 安装 tesseract2. Ubuntu-24.04 安装支持语言3. Windows 安装 tesseract4. Oracle Linux 8 安装 tesseract 1. Ubuntu-24.04 安装 tesseract sudo apt install tesseract-ocr sudo apt install libtesseract-devreference: https://tesseract-…...
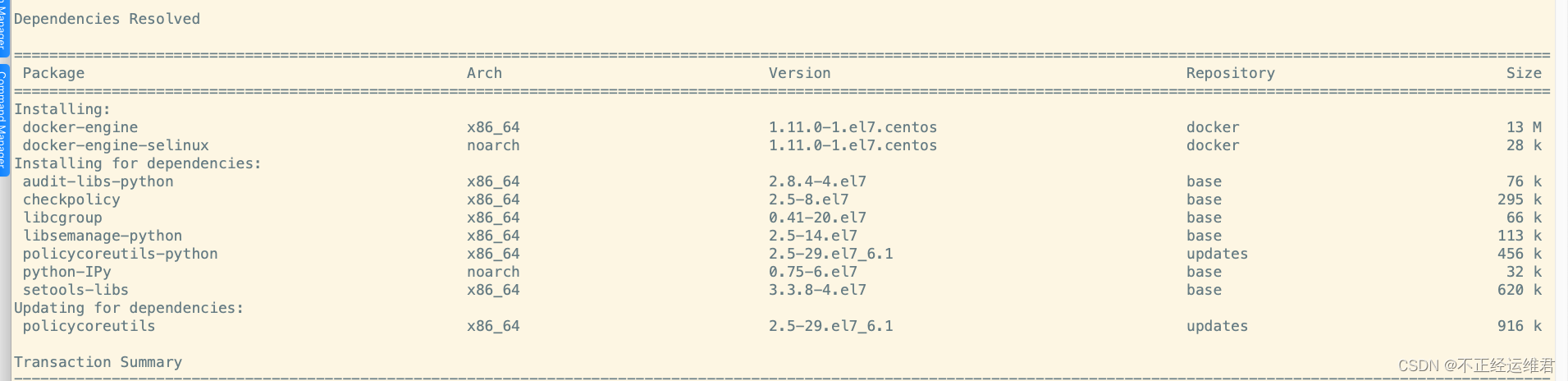
为适配kubelet:v0.4 安装指定版本的docker
系统版本信息 cat /etc/redhat-release CentOS Linux release 7.6.1810 (Core) iso 文件下载地址 https://vault.centos.org/7.6.1810/isos/x86_64/CentOS-7-x86_64-DVD-1810.iso0.4 版本的kubelet 报错信息记录 E0603 19:00:38.273720 44142 kubelet.go:734] Error synci…...

vivado CLOCK_REGION、CLOCK_ROOT
时钟区域 CLOCK_REGION属性用于将时钟缓冲区分配给 UltraScale设备,同时让Vivado放置程序将时钟缓冲区分配给最佳站点 在该区域内。 重要提示:对于UltraScale设备,不建议将时钟缓冲区固定到特定站点,因为 你可以在时钟上规划一个7…...

alphazero学习
AlphaGoZero是AlphaGo算法的升级版本。不需要像训练AlphaGo那样,不需要用人类棋局这些先验知识训练,用MCTS自我博弈产生实时动态产生训练样本。用MCTS来创建训练集,然后训练nnet建模的策略网络和价值网络。就是用MCTSPlayer产生的数据来训练和…...

剖析DeFi交易产品之UniswapV3:交易路由合约
本文首发于公众号:Keegan小钢 SwapRouter 合约封装了面向用户的交易接口,但不再像 UniswapV2Router 一样根据不同交易场景拆分为了那么多函数,UniswapV3 的 SwapRouter 核心就只有 4 个交易函数: exactInputSingle:指…...

Agent下载安装步骤
目录 一. 环境准备 二. 部署安装 三. Server端Web页面添加agent客户端 一. 环境准备 准备一台虚拟机,关闭防火墙和selinux,进行时间同步。 版本主机名IP系统zabbix6.4-agentweb1192.168.226.29Rocky_linux9.4 修改主机名 [rootlocalhost ~]# hostna…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...
