【链表OJ题(三)】链表中倒数第k个结点

📝个人主页:@Sherry的成长之路
🏠学习社区:Sherry的成长之路(个人社区)
📖专栏链接:数据结构
🎯长路漫漫浩浩,万事皆有期待
文章目录
- 链表OJ题(三)
- 1. 链表中倒数第k个结点
- 思路1--两次遍历
- 思路2-快慢指针
- 2.总结:
上一篇链表OJ题链接:【链表OJ题(二)】链表的中间节点
链表OJ题(三)
1. 链表中倒数第k个结点
链接:链表中倒数第k个结点
描述:
输入一个链表,输出该链表中倒数第k个结点。
示例1::
输入:
1,{1,2,3,4,5}
返回值:
{5}
思路1–两次遍历
和求链表的中间节点的方法一相似,为直接法。
要求链表的倒数第 k 个节点,那么就是删除链表正数第 len(链表长度) - k + 1 个节点。
举个例子,例如链表长度为 5,删除倒数第 2 个节点,就是删除链表正数第 4 个节点,推导出来就是第 len + 1 - k 个节点。
所以只要先算出链表长度,然后遍历到 len + 1 - k 个节点返回即可。
注意
1.在计算出链表总长度len<k或k<=0时,直接返回NULL。
2.传递的是空链表,直接返回NULL
/*
struct ListNode {int val;struct ListNode *next;ListNode(int x) : val(x), next(NULL) {}
};*/
struct ListNode* FindKthToTail(struct ListNode* pListHead, int k )
{struct ListNode*cur,*ans;cur=ans=pListHead;int len=0;while (cur) {cur=cur->next;len++;}if(k<=0||k>len)return NULL;for (int i=0; i<len-k; i++) {ans=ans->next;}return ans;
}

既然这道题目也可以用直接法,那么能否也适用于快慢指针?事实上可以,而且这道题的方法也很巧妙,接下来看思路2
思路2-快慢指针
在上一篇博客中我们也使用了快慢指针
给定一个快指针 fast 和一个慢指针 slow;我们要求链表倒数第 k 个节点,那么我们就先让快指针走 k 步;然后让 fast 和 slow 一起走,当 fast 走到空指针,这时 slow 为倒数第 k 个节点。

那么这里的原理是什么呢?
首先让 fast 走 k 步,让 fast 和 slow 的间隔为 k。链表的倒数第 k 个节点,就是正数 len + 1 - k 个节点,那么当 fast 走到空指针后,链表走完,那么现在 fast 走的距离就相当于链表的长度len + 1,fast 和 slow的间隔为 k ,那么现在的 slow 就为正数 len + 1 - k个节点,这时返回 slow就是倒数第 k 个节点。
注意:如果在 fast 走 k 步的过程中,fast 迭代为了空指针,这时直接返回空指针。
代码:
struct ListNode* FindKthToTail(struct ListNode* pListHead, int k )
{struct ListNode* fast, *slow;fast = slow = pListHead;if (pListHead == NULL)return NULL;// fast 先走 k 步while (k--)//走k次,(--k)走k-1次{// 放置 fast 先走到空if (fast == NULL){return NULL;}fast = fast->next;}// 迭代while (fast){slow = slow->next;fast = fast->next;}return slow;
}

2.总结:
今天我们通过两种思路分析并完成链表中倒数第k个结点这道链表OJ题目,也更加深层次了解和使用了快慢指针这个思路,在之后的题目中将再次出现它的使用。希望我的文章和讲解能对大家的学习提供一些帮助。
当然,本文仍有许多不足之处,欢迎各位小伙伴们随时私信交流、批评指正!我们下期见~

相关文章:

【链表OJ题(三)】链表中倒数第k个结点
📝个人主页:Sherry的成长之路 🏠学习社区:Sherry的成长之路(个人社区) 📖专栏链接:数据结构 🎯长路漫漫浩浩,万事皆有期待 文章目录链表OJ题(三)1. 链表…...

华为防火墙的学习
防火墙 - 含义和定义 什么是防火墙? 防火墙的工作原理 防火墙的区域: 包过滤防火墙----访问控制列表技术---三层技术 代理防火墙----中间人技术---应用层 状态防火墙---会话追踪技术---三层、四层 UTM---深度包检查技术----应用层 下一代防火墙 防火墙的…...
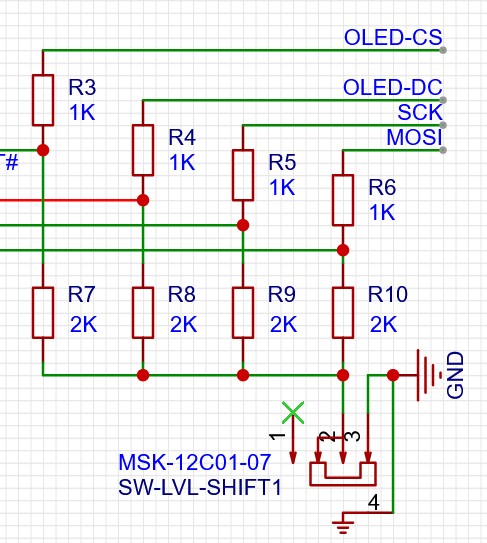
SPI 接口OLED 模块 - 兼容5V 和3.3V 电平
PCB 布局参考了老王0.8元128x32OLED显示屏转接板,开源项目地址:老王0.8元128x32OLED。 老王家买的屏幕放了快一年了,终于还是决定整个单独的模块,之前一直打算集成到开发板上的,不太灵活。相比那个转接板,主…...

css布局和定位
在Web开发中,CSS布局和定位是非常重要的技能。在这篇博客中,我们将深入探讨CSS布局和定位的概念、基本技术和最佳实践。 **CSS布局基础** ├── 盒模型 │ ├── 内边距 │ │ ├── padding │ │ ├── padding-top │ │ ├── p…...
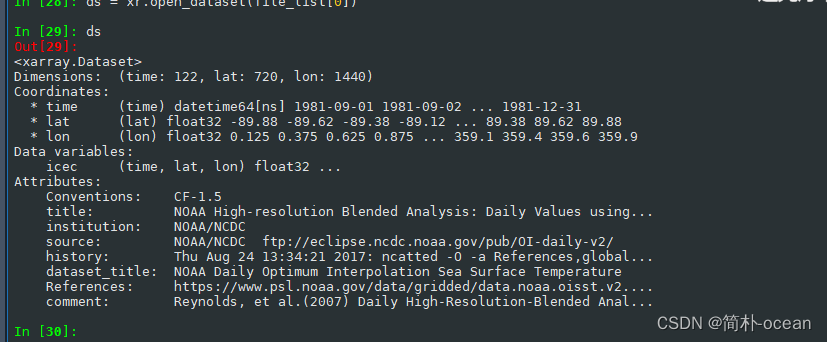
python -- 批量读取多个文件,并将每个文件中相同变量累加
python – 批量读取多个文件,并将每个文件中相同变量累加 情况描述 现有多个nc文件,位于同一个文件夹中,如下所示每个文件中都有相同的变量,想要读取每个文件中的变量然后将其加起来意思就是说: 文件1中的变量文件2中…...

低代码开发流程是怎么样的?
低代码开发流程是怎么样的?现在很多文章都在下功夫宣传what(低代码是什么)、why(为什么要用低代码),但是很少有文章能够系统讨论how(怎么用低代码)的问题。 所以我花3天的时间准备了…...

任何时候都不要在 for 循环中删除 List 集合元素!!!
首先说结论:无论什么场景,都不要对List使用for循环的同时,删除List集合元素,因为这么做就是不对的。 阿里开发手册也明确说明禁止使用foreach删除、增加List元素。 正确删除元素的方式是使用迭代器(Iteratorÿ…...

koa+Vite+vue3+ts+pinia构建项目
一、 初始化构建项目 npm create vite myProject -- --template vue-ts 注:Vite 需要 Node.js 版本 14.18,16。然而,有些模板需要依赖更高的 Node 版本才能正常运行,当你的包管理器发出警告时,请注意升级你的 Node 版…...
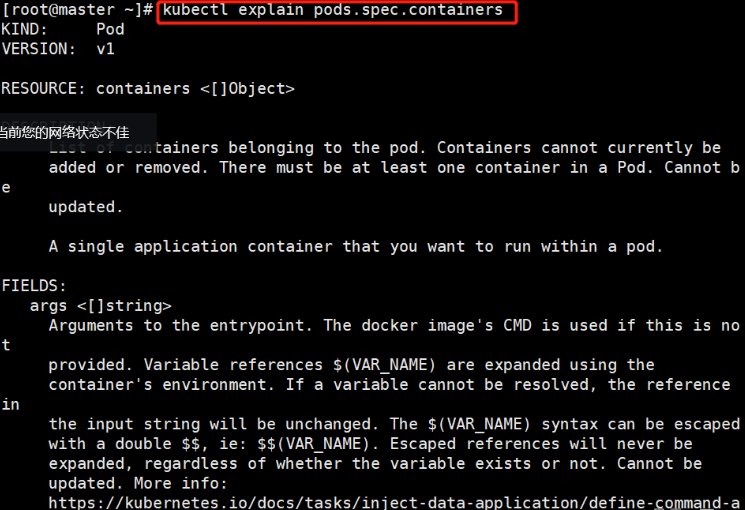
k8s-yaml文件
文章目录一、K8S支持的文件格式1、yaml和json的主要区别2、YAML语言格式二、YAML1、查看 API 资源版本标签2、编写资源配置清单2.1 编写 nginx-test.yaml 资源配置清单2.2 创建资源对象2.3 查看创建的pod资源3、创建service服务对外提供访问并测试3.1 编写nginx-svc-test.yaml文…...
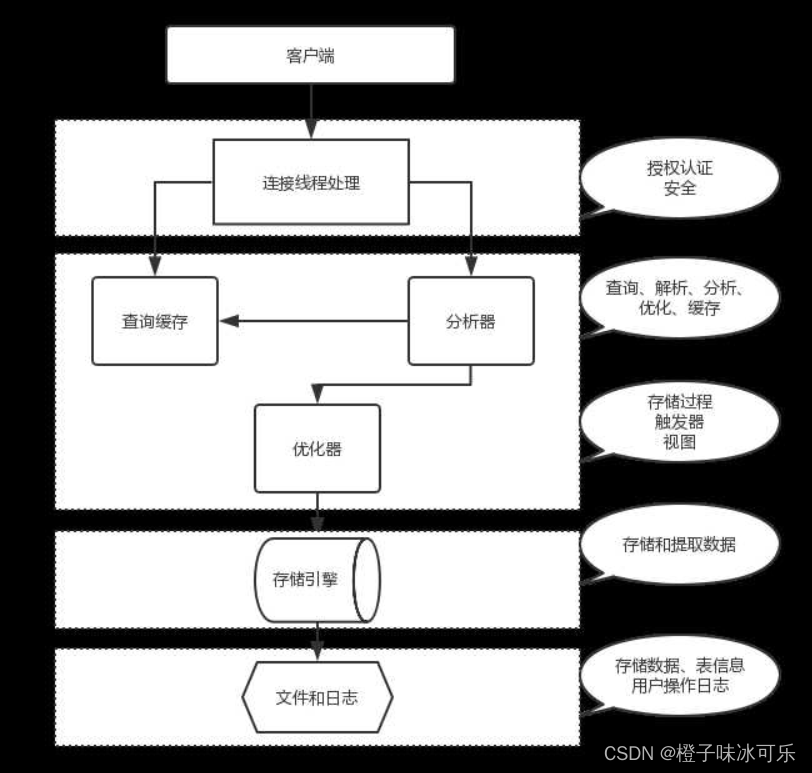
存储引擎
目录 ❤ MySQL存储引擎 什么是存储引擎? MySQL支持哪个存储引擎? ❤ 各种存储引擎的特性 概述 各种存储引擎的特性 各种搜索引擎介绍 ❤ 常用存储引擎及适用场景 ❤ 存储引擎在mysql中的使用 存储引擎相关sql语句 指定存储引擎建表 在建表时指定 在配置文件中…...

Go中 channel的使用
文章目录背景channel 简介使用说明声明发送和接受数据关闭channel使用示例背景 使用 sync 包和 context 包的工具可以实现多个协程之间互相协作, 但是没有一种很好的方式解决多个协程之间通信的问题. golang 作者 Rob Pike 说过一句话,不要通过共享内存来通信&…...

【C++】string OJ练习
文章目录1. 仅仅反转字母思路分析代码实现2. 字符串中的第一个唯一字符题目分析代码实现3. 《剑指offer》——替换空格解法一:寻找替换思路分析代码实现优化解法二:空间换时间思路分析代码实现4.字符串最后一个单词的长度思路分析代码实现5. 字符串相加思…...
进程间通信IPC
进程间通信IPC (InterProcess Communication) 一、进程间通信的概念 每个进程各自有不同的用户地址空间,任何一个进程的全局变量在另一个进程中都看不到,所以进程之间要交换数据必须通过内核,在内核中开辟一块缓冲区,进程1把数据…...
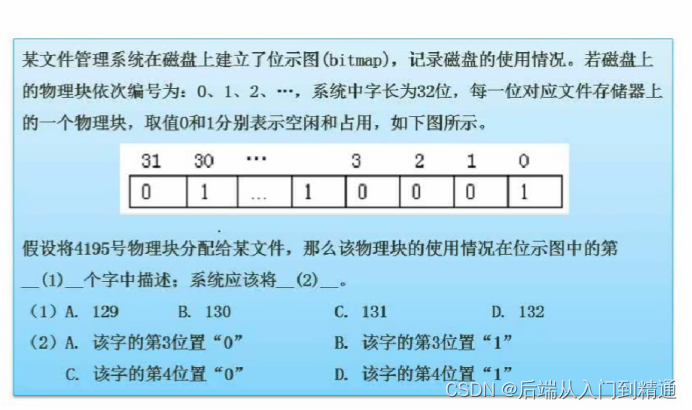
操作系统-页面淘汰算法(下)-软件设计(二十六)
操作系统-PV操作(上)-软件设计(二十五)https://blog.csdn.net/ke1ying/article/details/129476031 存储管理-分区存储组织 问:计算机系统内存大小为128k,当前系统分配情况如图,那么作业4再次申…...
)
23种设计模式-责任链模式(Android开发实际应用场景介绍)
什么是责任链模式 责任链模式是一种行为型设计模式,它的核心思想是将请求从一系列处理者中传递,直到其中一个处理者能够处理它为止。在这个过程中,请求可以被任何一个处理者处理,也可以被拒绝,直到有一个处理者能够处…...

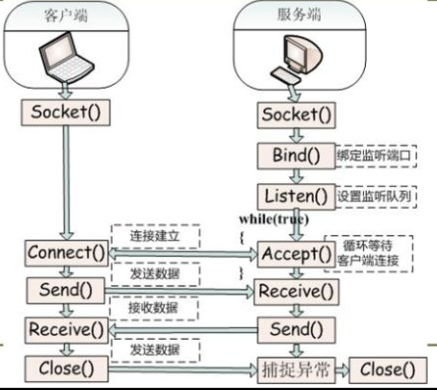
Socket+Select+Epoll笔记
讲到epoll,就必须了解Socket,上篇博客写了Socket的基本使用方法,步骤主要为创建一个socketsocket是进程之间通信的,那么进程通信如何找到这个socket呢?当然是端口号,所以socket就要和端口号进行绑定&#x…...

git查看最近修改的文件
git log --name-status 每次修改的文件列表, 显示状态 git log --name-only 每次修改的文件列表 git log --stat 每次修改的文件列表, 及文件修改的统计 git whatchanged 每次修改的文件列表 git whatchanged --stat 每次修改的文件列表, 及文件修改的统计 git show 显示最…...
】堆排序(二))
【算法基础(四)】堆排序(二)
堆排序(二) 把数组从零开始连续的一段 完全二叉树 size i 左 son 2*11 i 右 son 2*12 父 (i-1) / 2 堆是完全二叉树,分为大根堆和小根堆 在完全二叉树里,每一棵子数最大的值是头节点的值,就是大根堆 同理&…...

C++类型转换
C语言的转换是在变量前加类型名进行转换的,比如double pi 3.14;int a (int) pi;对于指针也是如此double* dptr πint* iptr (int*)dptr;虽然c兼容了C语言的转型方式,但是也做了很多限制,比如向上类型转换,在c中建议使用…...

Keil MDK6要来了,将嵌入式软件开发水平带到新高度,支持跨平台(2023-03-11)
注:这个是MDK6,不是MDK5 AC6,属于下一代MDK视频版: https://www.bilibili.com/video/BV16s4y157WF Keil MDK6要来了,将嵌入式软件开发水平带到新高度,支持跨平台一年一度的全球顶级嵌入式会展Embedded Wor…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

Axure 下拉框联动
实现选省、选完省之后选对应省份下的市区...
)
41道Django高频题整理(附答案背诵版)
解释一下 Django 和 Tornado 的关系? Django和Tornado都是Python的web框架,但它们的设计哲学和应用场景有所不同。 Django是一个高级的Python Web框架,鼓励快速开发和干净、实用的设计。它遵循MVC设计,并强调代码复用。Django有…...
MeanFlow:何凯明新作,单步去噪图像生成新SOTA
1.简介 这篇文章介绍了一种名为MeanFlow的新型生成模型框架,旨在通过单步生成过程高效地将先验分布转换为数据分布。文章的核心创新在于引入了平均速度的概念,这一概念的引入使得模型能够通过单次函数评估完成从先验分布到数据分布的转换,显…...
