算法的效率——时间复杂度和空间复杂度
文章目录
- 1. 算法效率
- 1.1 什么是算法
- 1.2 算法的好坏
- 2. 时间复杂度
- 2.1 什么是时间复杂度
- 2.2 时间复杂度的计算方法
- 2.3 大O的渐进表示法
- 2.4 常见时间复杂度计算举例
- 3. 空间复杂度
- 4. 常见复杂度对比
1. 算法效率
1.1 什么是算法
目前普遍认可对算法的定义是:算法是解决特定问题求解步骤的描述,在计算机中表现为指令的有限序列,并且每个指令表示一个或多个操作。
大白话就是计算的方法,通过该方法,可以达到我们预期的计算结果。
1.2 算法的好坏
最近“九转大肠”在网络上十分火爆,小伙在制作过程中,故意的保留了“原始风味”,令评委十分“粪怒”。那为什么同样是“九转大肠”,评价却如此不一样呢?评委点评看三个方面:做菜的材料、做菜的时间、菜的味道,三者缺一不可。

算法也是如此,在保证计算能出我们预期的结果的前提下,还需考虑效率。
即算法在编写成可执行程序后,运行时需要耗费时间资源和空间(内存)资源。因此衡量一个算法的好坏,一般是从时间和空间两个维度来衡量,即时间复杂度和空间复杂度。
小贴士:
时间复杂度主要衡量一个算法的运行快慢,而空间复杂度主要衡量一个算法运行所需要的额外空间。在计算机发展的早期,计算机的存储容量很小。所以对空间复杂度很是在乎。但是经过计算机行业的迅速发展,计算机的存储容量已经达到了很高的程度。所以我们如今已经不需要再特别关注一个算法的空间复杂度。
2. 时间复杂度
2.1 什么是时间复杂度
一个算法所花费的时间与其中语句的执行次数成正比例,总语句执行次数记为T(n)。在一般情况下,算法中基本操作重复执行的次数是问题规模n某个函数f(n),算法的时间量度记作T(n) = O(f(n))。它表示随着问题规模n的增大,算法执行时间的增长率和f(n) 增长率相同,称为算法的渐进时间复杂度,简称时间复杂度。
2.2 时间复杂度的计算方法
一个算法执行所耗费的时间,从理论上说,是不能算出来的,只有你把你的程序放在机器上跑起来,才能知道。但如果每个程序都需要上机测试,就会很麻烦。
我们只需计算出算法中的基本操作的执行次数即可。
例如:
//计算Func1中++count语句总共执行了多少次?
void Func1(int N)
{int count = 0;for (int i = 0; i < N; ++i){for (int j = 0; j < N; ++j){++count;}}for (int k = 0; k < 2 * N; ++k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}
Func1执行的基本操作次数: F(N) = N2 + 2*N + 10
在这里,我们并不需要计算出准确的次数,只需要算出该函数是是属于哪个量级。即找出函数式中对结果影响最大的那个。假设这里的N为无限大,那么后面的 2*N + 10对结果的影响就微乎其微。
所以不一定要计算精确的执行次数,而只需要大概执行次数,那么这里我们使用大O的渐进表示法。
2.3 大O的渐进表示法
大O符号(Big O notation):是用于描述函数渐进行为的数学符号。
推导大O阶方法:
- 用常数1取代运行时间中的所有加法常数。
- 在修改后的运行次数函数中,只保留最高阶项。
- 如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶。
用大O的渐进表示法以后,那么Func1的时间复杂度为 :O(N2)。
另外,有些算法的时间复杂度存在最好、平均和最坏情况。
例如,要用在长度为N的数组中查找某个数据:
- 最好的情况:第一次就找到
- 最坏的情况:第N次才找到
- 平均情况:N/2次找到
那我们该取哪种情况呢?举个例子,约了一个好朋友出来吃饭,预定时间12:00。
- 按预定时间到达12:00(最坏情况),那么就只能吃个饭。
- 都提前一小时到11:00(最好情况),先逛逛街,吃个饭、最后还能散散步。
- 提前半小时到11:30(平均情况),吃饭->散步->带回。
那么我们肯定是说12点到嘛,如果12点之前到,就会有额外的惊喜,如果直接告诉最好的情况,实际效果可能就没那么好。
所以时间复杂度在实际情况下,关注的是算法运算最坏情况。
2.4 常见时间复杂度计算举例
O(1)
// 计算Func1的时间复杂度
void Func1(int N)
{int count = 0;for (int k = 0; k < 100; ++ k){++count;}printf("%d\n", count);
}
基本操作执行了100次,是一个确定的值,通过推导大O阶的方法,无最高阶项,常数用1表示。即时间复杂度为O(1)。
O(n)
// 计算阶乘递归Fac的时间复杂度?
long long Fac(size_t N)
{if(0 == N)return 1;return Fac(N-1)*N;
}
基本操作递归了N次,最高阶项是N,通过推导大O阶的方法,只保留最高阶项。即时间复杂度为O(n)。
O(n2)
// 计算BubbleSort的时间复杂度?
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i-1] > a[i]){Swap(&a[i-1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}
这里是一个冒泡排序,基本操作最好的情况执行N次,最坏情况执行N*(N-1)/2次,时间复杂度看最坏情况,再通过推导大O阶的方法,最高阶项为N2。即时间复杂度为O(n2)。
O(logN)
// 计算BinarySearch的时间复杂度?
int BinarySearch(int* a, int n, int x)
{assert(a);int begin = 0;int end = n-1;// [begin, end]:begin和end是左闭右闭区间,因此有=号while (begin <= end){int mid = begin + ((end-begin)>>1);if (a[mid] < x)begin = mid+1;else if (a[mid] > x)end = mid-1;elsereturn mid;}return -1;
}
这里是一个二分查找的算法,基本操作执行情况是1次,最坏情况是O(logN)次 (ps:logN在算法分析中表示底数是2),每次查找减一半,即时间复杂度为O(logN)。
小贴士:
在理论上,二分查找是一个非常牛的算法,例如在10000个数据中,它最坏情况下,大概10次就找出来了;如果用冒泡排序,则最坏需要查找 100002次,这二者的差别十分之大。但是二分查找有一个前提就是,数据序列必须是一个有序序列,这就带来了很大的局限性。
3. 空间复杂度
空间复杂度也是一个数学表达式,是一个对算法在运行过程中临时占用存储空间大小的量度,算的是变量的个数,同时也使用大O渐进表示法。
函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了,因此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定。
示例1:
// 计算阶乘递归Fac的空间复杂度?
long long Fac(size_t N)
{if(N == 0)return 1;return Fac(N-1)*N;
}
在这里,调用了N次Fac阶乘函数,每调用一次,就创建一个函数栈帧,那个就开辟了N个内存空间,即空间复杂度为O(n)。
示例2:
// 计算斐波那契递归Fib的空间复杂度?
long long Fib(size_t N)
{if(N < 3)return 1;return Fib(N-1) + Fib(N-2);
}
该算法的时间复杂度为O(2n),那么额外申请的空间也是 2n 吗?
这里的递归并不是我们想象中一层一层往下面调用。
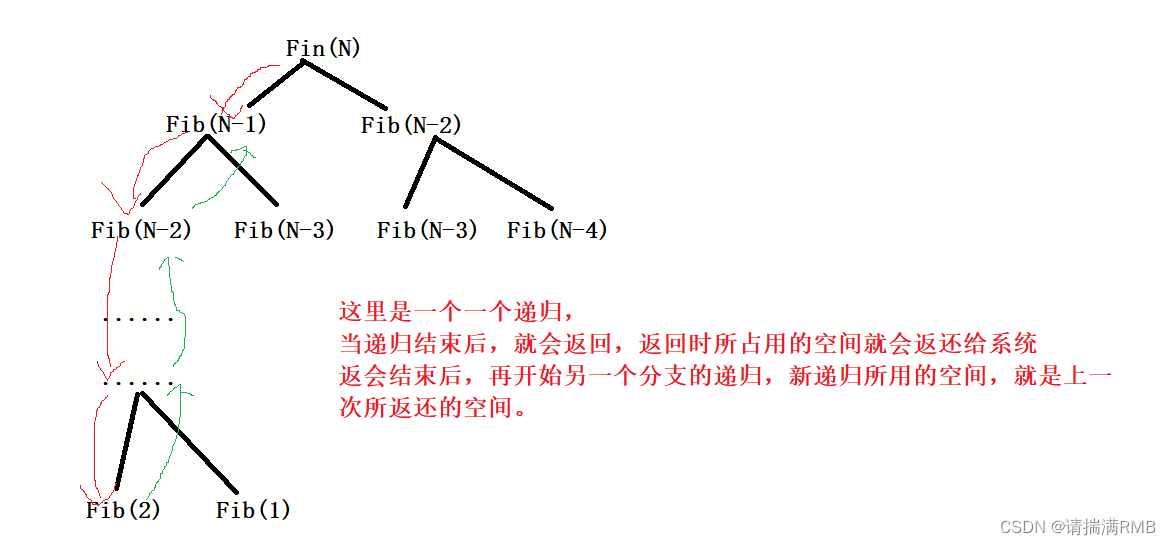
通过这两个样例的比较,我们可以总结出时间复杂度和空间复杂度的特性:
- 时间是一去不复返的,不可重复利用
- 空间用了需要返还,可以重复利用
4. 常见复杂度对比
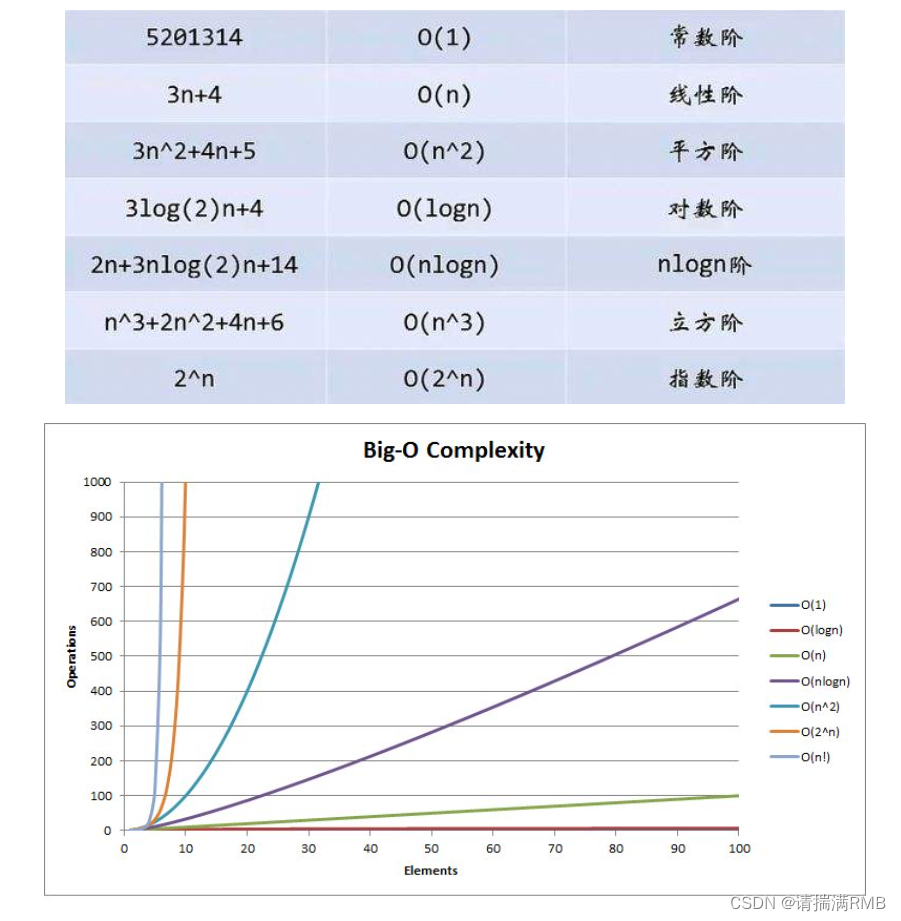
相关文章:

算法的效率——时间复杂度和空间复杂度
文章目录1. 算法效率1.1 什么是算法1.2 算法的好坏2. 时间复杂度2.1 什么是时间复杂度2.2 时间复杂度的计算方法2.3 大O的渐进表示法2.4 常见时间复杂度计算举例3. 空间复杂度4. 常见复杂度对比1. 算法效率 1.1 什么是算法 目前普遍认可对算法的定义是:算法是解决…...

2021年 第12届 蓝桥杯 Java B组 省赛真题详解及小结【第1场省赛 2021.04.18】
总分:5 一、试题A:ASC 得分:5分 本题总分:5 分 【问题描述】 已知大写字母 A 的 ASCII 码为 65,请问大写字母 L 的 ASCII 码是多少? 【答案提交】 这是一道结果填空的题,你只需要算出结果后提…...
透过等待看数据库
等待分类与解决基本流程步骤1.定位问题系统等待往往能直观的反映出系统问题。通过一些常见的等待类型,同样可以找到系统瓶颈,结合性能计数器往往定位更准确。如:系统中存在大量IO类等待,那么可能表示你的磁盘或内存是语句运行缓慢…...
中科亿海微FPGA
国产FPGA中,紫光、安路、高云称得上是三小龙,其他的半斤八两,中科亿海微也算是其中之一。 其产品为亿海神针系列,如下: 可见其最小规模也有9.2KLUT,最大竟有136K之多了,对比其他国产࿰…...

【链表OJ题(三)】链表中倒数第k个结点
📝个人主页:Sherry的成长之路 🏠学习社区:Sherry的成长之路(个人社区) 📖专栏链接:数据结构 🎯长路漫漫浩浩,万事皆有期待 文章目录链表OJ题(三)1. 链表…...

华为防火墙的学习
防火墙 - 含义和定义 什么是防火墙? 防火墙的工作原理 防火墙的区域: 包过滤防火墙----访问控制列表技术---三层技术 代理防火墙----中间人技术---应用层 状态防火墙---会话追踪技术---三层、四层 UTM---深度包检查技术----应用层 下一代防火墙 防火墙的…...
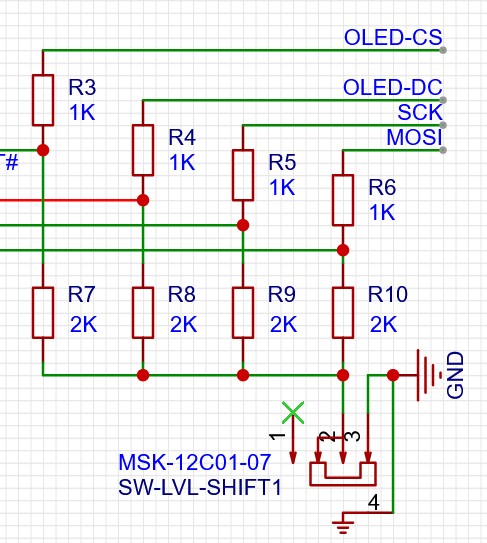
SPI 接口OLED 模块 - 兼容5V 和3.3V 电平
PCB 布局参考了老王0.8元128x32OLED显示屏转接板,开源项目地址:老王0.8元128x32OLED。 老王家买的屏幕放了快一年了,终于还是决定整个单独的模块,之前一直打算集成到开发板上的,不太灵活。相比那个转接板,主…...

css布局和定位
在Web开发中,CSS布局和定位是非常重要的技能。在这篇博客中,我们将深入探讨CSS布局和定位的概念、基本技术和最佳实践。 **CSS布局基础** ├── 盒模型 │ ├── 内边距 │ │ ├── padding │ │ ├── padding-top │ │ ├── p…...
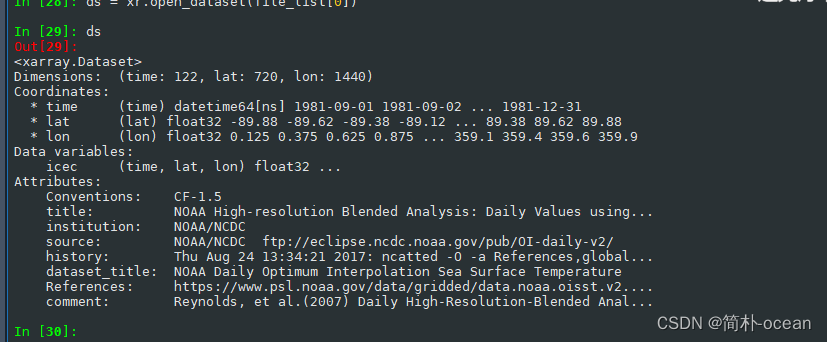
python -- 批量读取多个文件,并将每个文件中相同变量累加
python – 批量读取多个文件,并将每个文件中相同变量累加 情况描述 现有多个nc文件,位于同一个文件夹中,如下所示每个文件中都有相同的变量,想要读取每个文件中的变量然后将其加起来意思就是说: 文件1中的变量文件2中…...

低代码开发流程是怎么样的?
低代码开发流程是怎么样的?现在很多文章都在下功夫宣传what(低代码是什么)、why(为什么要用低代码),但是很少有文章能够系统讨论how(怎么用低代码)的问题。 所以我花3天的时间准备了…...

任何时候都不要在 for 循环中删除 List 集合元素!!!
首先说结论:无论什么场景,都不要对List使用for循环的同时,删除List集合元素,因为这么做就是不对的。 阿里开发手册也明确说明禁止使用foreach删除、增加List元素。 正确删除元素的方式是使用迭代器(Iteratorÿ…...

koa+Vite+vue3+ts+pinia构建项目
一、 初始化构建项目 npm create vite myProject -- --template vue-ts 注:Vite 需要 Node.js 版本 14.18,16。然而,有些模板需要依赖更高的 Node 版本才能正常运行,当你的包管理器发出警告时,请注意升级你的 Node 版…...
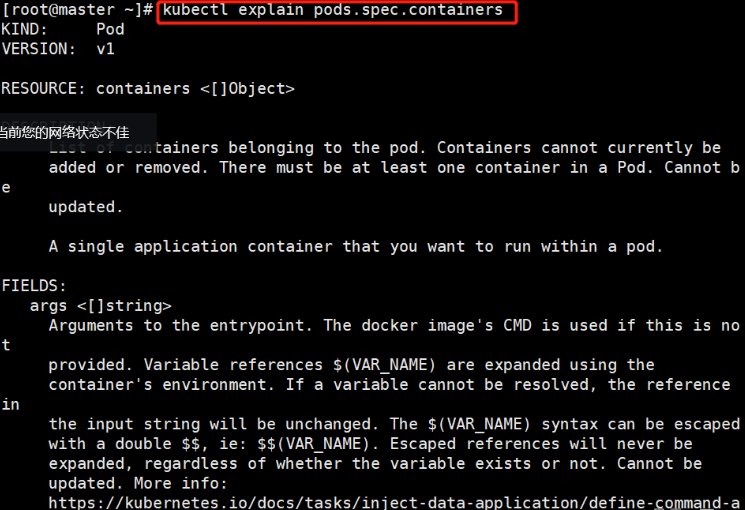
k8s-yaml文件
文章目录一、K8S支持的文件格式1、yaml和json的主要区别2、YAML语言格式二、YAML1、查看 API 资源版本标签2、编写资源配置清单2.1 编写 nginx-test.yaml 资源配置清单2.2 创建资源对象2.3 查看创建的pod资源3、创建service服务对外提供访问并测试3.1 编写nginx-svc-test.yaml文…...
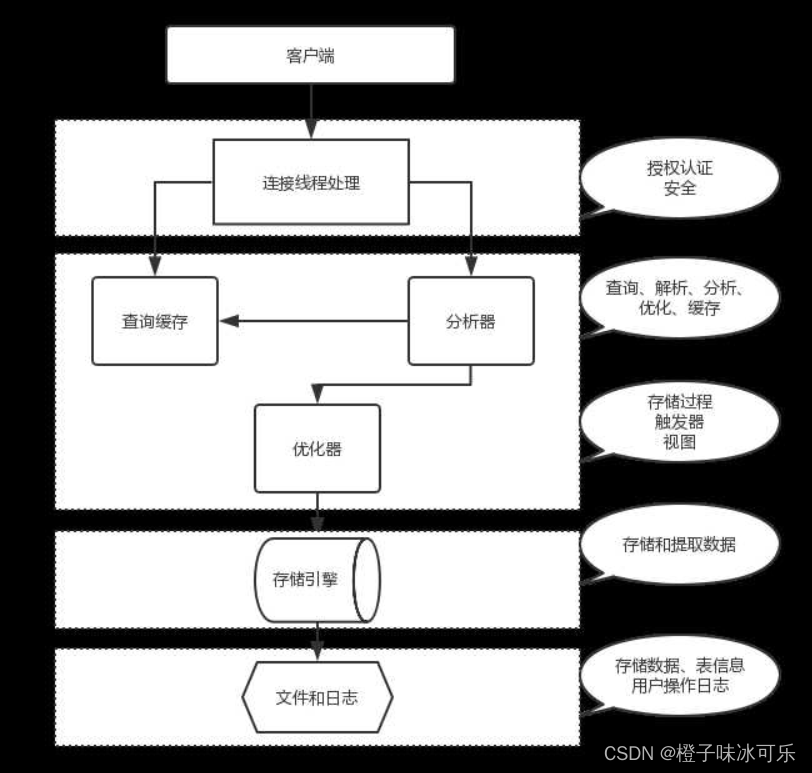
存储引擎
目录 ❤ MySQL存储引擎 什么是存储引擎? MySQL支持哪个存储引擎? ❤ 各种存储引擎的特性 概述 各种存储引擎的特性 各种搜索引擎介绍 ❤ 常用存储引擎及适用场景 ❤ 存储引擎在mysql中的使用 存储引擎相关sql语句 指定存储引擎建表 在建表时指定 在配置文件中…...

Go中 channel的使用
文章目录背景channel 简介使用说明声明发送和接受数据关闭channel使用示例背景 使用 sync 包和 context 包的工具可以实现多个协程之间互相协作, 但是没有一种很好的方式解决多个协程之间通信的问题. golang 作者 Rob Pike 说过一句话,不要通过共享内存来通信&…...

【C++】string OJ练习
文章目录1. 仅仅反转字母思路分析代码实现2. 字符串中的第一个唯一字符题目分析代码实现3. 《剑指offer》——替换空格解法一:寻找替换思路分析代码实现优化解法二:空间换时间思路分析代码实现4.字符串最后一个单词的长度思路分析代码实现5. 字符串相加思…...
进程间通信IPC
进程间通信IPC (InterProcess Communication) 一、进程间通信的概念 每个进程各自有不同的用户地址空间,任何一个进程的全局变量在另一个进程中都看不到,所以进程之间要交换数据必须通过内核,在内核中开辟一块缓冲区,进程1把数据…...
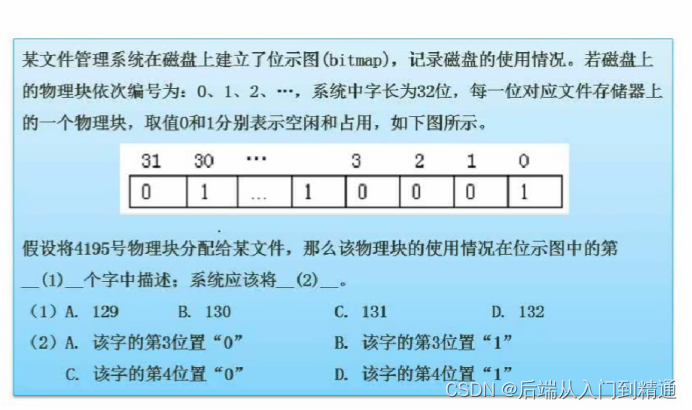
操作系统-页面淘汰算法(下)-软件设计(二十六)
操作系统-PV操作(上)-软件设计(二十五)https://blog.csdn.net/ke1ying/article/details/129476031 存储管理-分区存储组织 问:计算机系统内存大小为128k,当前系统分配情况如图,那么作业4再次申…...
)
23种设计模式-责任链模式(Android开发实际应用场景介绍)
什么是责任链模式 责任链模式是一种行为型设计模式,它的核心思想是将请求从一系列处理者中传递,直到其中一个处理者能够处理它为止。在这个过程中,请求可以被任何一个处理者处理,也可以被拒绝,直到有一个处理者能够处…...

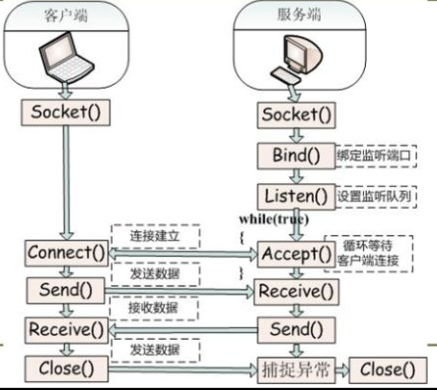
Socket+Select+Epoll笔记
讲到epoll,就必须了解Socket,上篇博客写了Socket的基本使用方法,步骤主要为创建一个socketsocket是进程之间通信的,那么进程通信如何找到这个socket呢?当然是端口号,所以socket就要和端口号进行绑定&#x…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...

0x-3-Oracle 23 ai-sqlcl 25.1 集成安装-配置和优化
是不是受够了安装了oracle database之后sqlplus的简陋,无法删除无法上下翻页的苦恼。 可以安装readline和rlwrap插件的话,配置.bahs_profile后也能解决上下翻页这些,但是很多生产环境无法安装rpm包。 oracle提供了sqlcl免费许可,…...

计算机系统结构复习-名词解释2
1.定向:在某条指令产生计算结果之前,其他指令并不真正立即需要该计算结果,如果能够将该计算结果从其产生的地方直接送到其他指令中需要它的地方,那么就可以避免停顿。 2.多级存储层次:由若干个采用不同实现技术的存储…...

【汇编逆向系列】六、函数调用包含多个参数之多个整型-参数压栈顺序,rcx,rdx,r8,r9寄存器
从本章节开始,进入到函数有多个参数的情况,前面几个章节中介绍了整型和浮点型使用了不同的寄存器在进行函数传参,ECX是整型的第一个参数的寄存器,那么多个参数的情况下函数如何传参,下面展开介绍参数为整型时候的几种情…...
