并查集(不相交集)详解
目录
一.并查集
1.什么是并查集
2.并查集的基本操作
3.并查集的应用
4.力扣上的题目
二.三大操作
1.初始化
2.查找
3.合并
三.省份数量
1.题目描述
2.问题分析
3.代码实现
四.冗余连接
1.题目描述
2.问题分析
3.代码实现
一.并查集
1.什么是并查集
并查集(Disjoint-set Union 或 Union-find)是一种数据结构,用于维护一些不相交(disjoint)的集合,支持合并两个集合以及判断两个元素是否属于同一个集合。
并查集可以使用树来实现,每个集合可以看做是一棵树,代表元素是根节点。使用路径压缩可以减少查找操作的时间复杂度,使用按秩合并可以减少合并操作的时间复杂度,使得并查集的时间复杂度可以达到近乎常数级别,因此在一些算法中广泛应用,比如 Kruskal 算法和 Tarjan 算法。
2.并查集的基本操作
- 初始化:将每个元素初始化为单独的集合,每个集合的代表元素就是自己;
- 查找:给定一个元素,找到它所属的集合的代表元素;
- 合并:将两个集合合并成一个集合,即将其中一个集合的代表元素作为另一个集合的代表元素的子节点。
3.并查集的应用
并查集是一种用于维护集合(组)的数据结构,它通常用于解决一些离线查询、动态连通性和图论等相关问题。
其中最常见的应用场景是解决图论中的连通性问题,例如判断图中两个节点是否连通、查找图的连通分量、判断图是否为一棵树等等。并查集可以快速地合并两个节点所在的集合,以及查询两个节点是否属于同一个集合,从而有效地判断图的连通性。
并查集还可以用于解决一些离线查询问题,例如静态连通性查询和最小生成树问题,以及一些动态连通性问题,例如支持动态加边和删边的连通性问题。
总之,如果需要维护集合(组)的连通性信息,就可以考虑使用并查集。
现在举一个现实中的问题,判断一个人是否属于一个家族,通常一个家族里面两个人可能不是彼此认识的,但是A和B是亲属关系,B和C是亲属关系,此时我们可以判断出A和C就是亲属关系

由于家族关系可能错综复杂,这个时候我们是否可以找一个代表,这个人来代表这个家族,比如选择A来代表家族A,D来代表家族B,那么只要你和A有关系,你就是属于A家族的,你和D有关系,你就是属于B家族的
并查集就是解决这样的问题的.
4.力扣上的题目
以下是一些力扣(LeetCode)上关于并查集(Union Find)的题目:
-
朋友圈(547) https://leetcode-cn.com/problems/friend-circles/
-
冗余连接(684) https://leetcode-cn.com/problems/redundant-connection/
-
冗余连接 II(685) https://leetcode-cn.com/problems/redundant-connection-ii/
-
岛屿数量(200) https://leetcode-cn.com/problems/number-of-islands/
-
连通网络的操作次数(1319) https://leetcode-cn.com/problems/number-of-operations-to-make-network-connected/
-
表示数值的字符串(剑指 Offer 20) https://leetcode-cn.com/problems/biao-shi-shu-zhi-de-zi-fu-chuan-lcof/
-
最大连通面积(面试题 16.19) https://leetcode-cn.com/problems/pond-sizes-lcci/
-
能否连接形成区域(面试题 16.19) https://leetcode-cn.com/problems/pond-sizes-lcci/
-
合并账户(721) https://leetcode-cn.com/problems/accounts-merge/
-
判断能否形成等差数列(1502) https://leetcode-cn.com/problems/can-make-arithmetic-progression-from-sequence/
以上是一些力扣上的并查集题目,建议在练习时,先自己尝试思考解法,如果卡在某个地方,可以查看题解或者向其他程序员求助。
二.三大操作
1.初始化
我们把数组初始化-1,具体的作用我们之后再来分析具体的用处,具体含义就是,这个负数的相反数为这棵树的高度-1

public void init(int[] parent) {//初始值设置为-1for (int i = 0; i < parent.length; ++i) {parent[i] = -1;}}2.查找
不进行路径压缩的查找简单粗暴的,它的目的就是为了找到结点i的根结点,直接看代码
public int find(int[] parent, int i) {if (parent[i] < 0) {//当前结点为根结点,终止return i;} else {return parent[i]; //返回父节点}}这个时候我们来研究一下进行路径压缩的查找方式,我们需要合并0和4,如果我们只是粗暴的合并的话,这个时候0指向3,这个时候其实的查询长度就是越来越长,时间复杂度为O(n)

所以这个时候我们不进行路径压缩,压缩之后的图是这样的,这个时候时间复杂度大大降低,我们每次查找根结点的时候,只需要查找一次(递归一次)便可以找到根结点
进行路径压缩的查找方法要进行两个操作,最终目的肯定还是要找寻到根结点,但是其次他也进行了路径的压缩,例如下图一样,把本来的4指向3,修改成了4指向了2,其实可以精炼成一句话:找到根结点,并且把路径上所有节点的父亲结点修改为根结点.这样树的高度就变成了1(只含有一个结点(根结点)的高度为0).
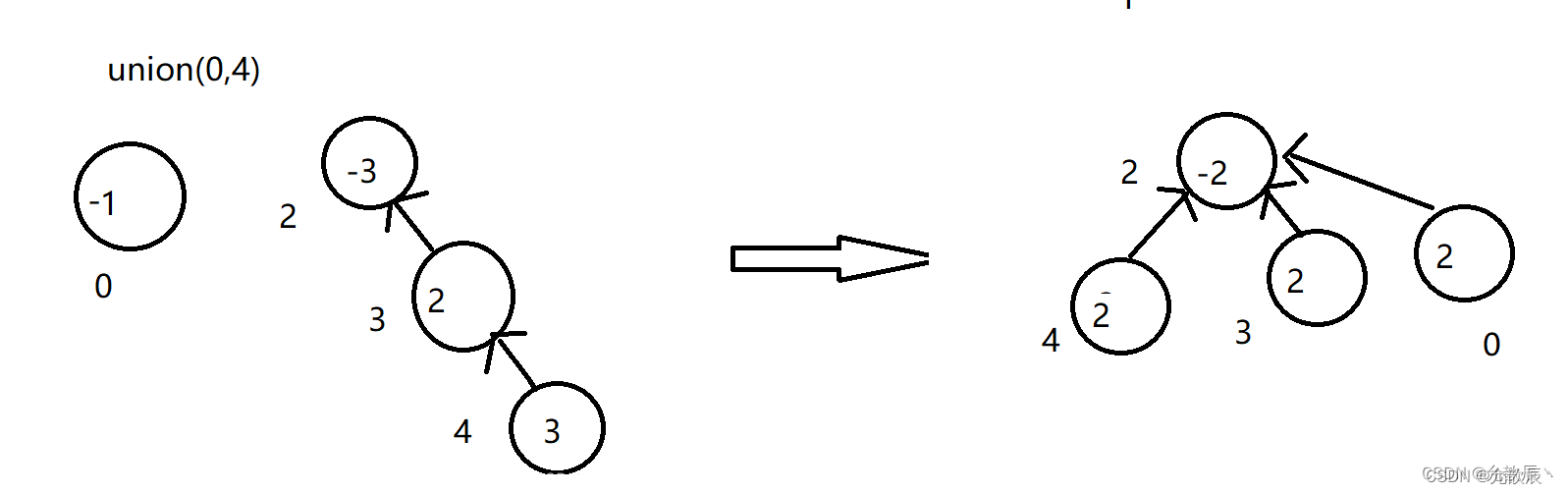
public int find(int[] parent, int i) {if (parent[i] < 0) {//当前结点为根结点,终止return i;} else {parent[i] = find(parent, parent[i]); //父节点设为根结点return parent[i]; //返回父节点}}3.合并
合并操作也可以简单粗暴的进行合成,我们只需要找到各自的祖先,任意的将一个合并到另一个上边即可,直接看代码
public void union(int[] parent, int i, int j) {int i_parent = find(parent, i);//寻找i的根结点int j_parent = find(parent, j);//寻找j的根结点parent[i_parent]=j_parent;//将根结点为i_parent的树合并到根结点j_parent上}如果我们这个时候进行合并可能会出现这种情况,也就是一个高度较大的数合并到了一个高度较小的树上面,这个时候树的高度就会增加,如果我们是高度小的树合并到高度较大的树上边(两颗树的高度不相等),这个时候树的高度便不会增加,自然查找的时候会更加快速的查找到.

进行按秩(树的高度)进行合并
这种合并方式就是为了解决上面所提到的问题,合并是便会是这种情况,但是我们如果判断两棵树的高度大小呢,这个时候就可以解释以下初始化的为-1的目的了,一:如果当前结点的值为负数,可以判断当前结点为根结点,二.当前结点越小(也就是相反数越大),说明当前树的高度越大,我们只需要把更大的根结点的值合并到更小的根结点值上,便可以解决这个问题了.

这个时候存在一个特殊情况,也就是两棵树的高度一样高.这个时候无论如何进行合并,树的高度度会增加,因此这个时候我们可以把一个根结点合并到另一个根结点上,并把合并到的根结点的值减一
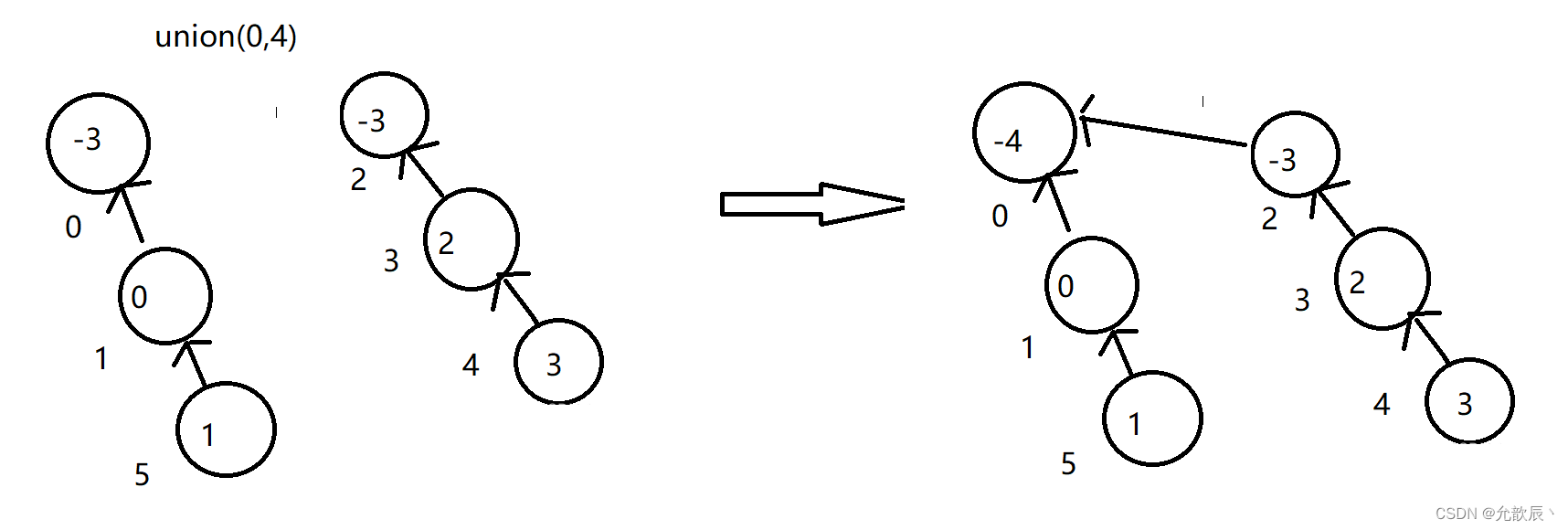
public void union(int[] parent, int i, int j) {int i_parent = find(parent, i);//寻找i的根结点int j_parent = find(parent, j);//寻找j的根结点if (i_parent != j_parent) {//此时的根结点相同,没有合并的必要if (parent[i_parent] < parent[j_parent]) {//此时表示i_parent的秩比j_parent的秩大parent[j_parent] = i_parent;//把j_parent合并到i_parent上} else {if (parent[i_parent] == parent[j_parent]) {parent[j_parent]--;}parent[i_parent] = j_parent;//把i_parent合并到j_parent上}}}三.省份数量
1.题目描述
有
n个城市,其中一些彼此相连,另一些没有相连。如果城市a与城市b直接相连,且城市b与城市c直接相连,那么城市a与城市c间接相连。省份 是一组直接或间接相连的城市,组内不含其他没有相连的城市。
给你一个
n x n的矩阵isConnected,其中isConnected[i][j] = 1表示第i个城市和第j个城市直接相连,而isConnected[i][j] = 0表示二者不直接相连。返回矩阵中 省份 的数量。
力扣:力扣
2.问题分析
这是一道很典型的并查集问题,题目的意思就是城市之间相连就是一个省份,把相连的城市合并为一颗树,最终就是寻找有多少个根结点(有多少颗树),也就是parent[i]有多少个是小于0的值,就是一棵树,最终返回数量就可以了
3.代码实现
public void init(int[] parent) {//初始值设置为-1for (int i = 0; i < parent.length; ++i) {parent[i] = -1;}}public int find(int[] parent, int i) {if (parent[i]<0) {return i;} else {parent[i] = find(parent, parent[i]); //父节点设为根结点return parent[i]; //返回父节点}}public void union(int[] parent, int i, int j) {int i_parent = find(parent, i);//寻找i的祖先int j_parent = find(parent, j);//寻找j的祖先if (i_parent != j_parent) {//此时的祖先相同,没有合并的必要if (parent[i_parent] < parent[j_parent]) {//此时表示i_parent的秩比j_parent的秩大parent[j_parent] = i_parent;//把j_parent合并到i_parent上} else {if (parent[i_parent] == parent[j_parent]) {parent[j_parent]--;}parent[i_parent] = j_parent;//把i_parent合并到j_parent上}}}public int findCircleNum(int[][] isConnected) {int[] parent = new int[isConnected.length];init(parent);for (int i = 0; i < isConnected.length; ++i) {for (int j = i + 1; j < isConnected[0].length; ++j) {if (isConnected[i][j] == 1) {union(parent, i, j);}}}int cnt = 0;for (int i = 0; i < parent.length; ++i) {if (parent[i] < 0)cnt++;}return cnt;}四.冗余连接
1.题目描述
树可以看成是一个连通且 无环 的 无向 图。
给定往一棵
n个节点 (节点值1~n) 的树中添加一条边后的图。添加的边的两个顶点包含在1到n中间,且这条附加的边不属于树中已存在的边。图的信息记录于长度为n的二维数组edges,edges[i] = [ai, bi]表示图中在ai和bi之间存在一条边。请找出一条可以删去的边,删除后可使得剩余部分是一个有着
n个节点的树。如果有多个答案,则返回数组edges中最后出现的边。
力扣:力扣
2.问题分析
题目的意思就是不能出现环,也就是如果两个两个点已经连通了,这个时候不能再在这两个点添加一条边,这个时候就冗余了,我们都知道一个连通分量有n个顶点,n-1条边,而这道题一共有n条边,我们需要寻找的就是这一条冗余的边,当find(parent,i,j)的根结点一样的时候,这个时候这两个顶点之间的边一定是冗余的,找到这样的一条边即可.
3.代码实现
public void init(int[] parent) {for (int i = 0; i < parent.length; ++i) {parent[i] = -1;}}public int find(int[] parent, int i) {if (parent[i] < 0)return i;else {parent[i] = find(parent, parent[i]);return parent[i];}}public void union(int[] parent, int i, int j) {int i_parent = find(parent, i);int j_parent = find(parent, j);if (i_parent != j_parent) {if (parent[i_parent] < parent[j_parent]) {parent[j_parent] = i_parent;} else {if (parent[i_parent] == parent[j_parent]) {parent[j_parent]--;}parent[i_parent] = j_parent;}}}public int[] findRedundantConnection(int[][] edges) {int[] parent = new int[edges.length+1];init(parent);for (int i = 0; i < edges.length; ++i) {if (find(parent, edges[i][0]) != find(parent, edges[i][1])) {union(parent, edges[i][0], edges[i][1]);} else {return edges[i];}}return null;}相关文章:

并查集(不相交集)详解
目录 一.并查集 1.什么是并查集 2.并查集的基本操作 3.并查集的应用 4.力扣上的题目 二.三大操作 1.初始化 2.查找 3.合并 三.省份数量 1.题目描述 2.问题分析 3.代码实现 四.冗余连接 1.题目描述 2.问题分析 3.代码实现 一.并查集 1.什么是并查集 并查集&…...

10个最频繁用于解释机器学习模型的 Python 库
文章目录什么是XAI?可解释性实践的步骤技术交流1、SHAP2、LIME3、Eli54、Shapash5、Anchors6、BreakDown7、Interpret-Text8、aix360 (AI Explainability 360)9、OmniXAI10、XAI (eXplainable AI)XAI的目标是为模型的行为和决定提供有意义的解释,本文整理…...

final关键字:我偏不让你继承
哈喽,小伙伴们大家好,我是兔哥呀,今天就让我们继续这个JavaSE成神之路! 这一节啊,咱们要学习的内容是Java所有final关键字。 之前呢,我们学习了继承,这大大提高了代码的灵活性和复用性。但是总…...

8大主流编程语言的适用领域,你可能选错了语言
很多人学编程经常是脑子一热然后就去网上一搜资源就开始学习了,但学到了后面发现目前所学的东西并不是自己最喜欢的,好像自己更喜欢另一个技术,感觉自己学错了,于是乎又去学习别的东西。 结果竹篮打水一场空,前面所付…...

关于Python库的问题
关于Python库的问题 问题1: ModuleNotFoundError: No module named ‘requests’ Python库 Pycharm使用Requests库时报错: No module named requests’解决方法 未安装requests库,使用"pip install requests"命令安装 依然提示P…...
)
好记性不如烂笔头(2)
概述:用来记录一些小技巧。 1.查看MyBatis执行的sql 类:org.apache.ibatis.mapping.MappedStatement方法:getBoundSql(Object parameterObject)在IDEA的Evaluate Expression查看sql:boundSql.getSql() 2.maven仓库地址为https&…...
Java for循环嵌套for循环,你需要懂的代码性能优化技巧
前言 本篇分析的技巧点其实是比较常见的,但是最近的几次的代码评审还是发现有不少兄弟没注意到。 所以还是想拿出来说下。 正文 是个什么场景呢? 就是 for循环 里面还有 for循环, 然后做一些数据匹配、处理 这种场景。 我们结合实例代码来…...

关于我拒绝了腾讯测试开发岗offer这件事
2022年刚开始有了向要跳槽的想法,之前的公司不能算大厂但在重庆也算是数一数二。开始跳槽的的时候我其实挺犹豫的 其实说是有跳槽的想法在2022年过年的时候就有了,因为每年公司3月会有涨薪的机会,所以想着看看那能不能涨(其实还是…...

从GPT到GPT-3:自然语言处理领域的prompt方法
❤️觉得内容不错的话,欢迎点赞收藏加关注😊😊😊,后续会继续输入更多优质内容❤️👉有问题欢迎大家加关注私戳或者评论(包括但不限于NLP算法相关,linux学习相关,读研读博…...
Git代码提交规范
Git 代码规范Git 每次提交代码,都是需要写 Commit message(提交说明),否则就不允许提交。Commit message 的格式 (三部分):Heaher ----- 必填type ---必需scope --- 可选subject --- 必需Body ---- 可省略Footer ---- …...

【JavaScript速成之路】JavaScript内置对象--Math和Date对象
📃个人主页:「小杨」的csdn博客 🔥系列专栏:【JavaScript速成之路】 🐳希望大家多多支持🥰一起进步呀! 文章目录前言1,Math对象1.1,常用属性方法1.1.1,获取x的…...
(自用POC)Fortinet-CVE-2022-40684
本文转载于:https://mp.weixin.qq.com/s?__bizMzIzNDU5Mzk2OQ&mid2247485332&idx1&sn85931aa474f1ae2c23a66bf6486eec63&chksme8f54c4adf82c55c44bc7b1ea919d44d377e35a18c74f83a15e6e20ec6c7bc65965dbc70130d&mpshare1&scene23&srcid…...

ConvNeXt V2实战:使用ConvNeXt V2实现图像分类任务(二)
文章目录训练部分导入项目使用的库设置随机因子设置全局参数图像预处理与增强读取数据设置Loss设置模型设置优化器和学习率调整算法设置混合精度,DP多卡,EMA定义训练和验证函数训练函数验证函数调用训练和验证方法运行以及结果查看测试热力图可视化展示完…...

【人工智能与深度学习】基于正则化潜在可变能量的模型
【人工智能与深度学习】基于正则化潜在可变能量的模型 正则化潜变量能量基础模型稀疏编码FISTALISTA稀疏编码示例卷积稀疏编码自然图像上的卷积稀疏编码可变自动编码器正则化潜变量能量基础模型 具有潜在变量的模型能够生成预测分布 y ‾ \overline{y}...
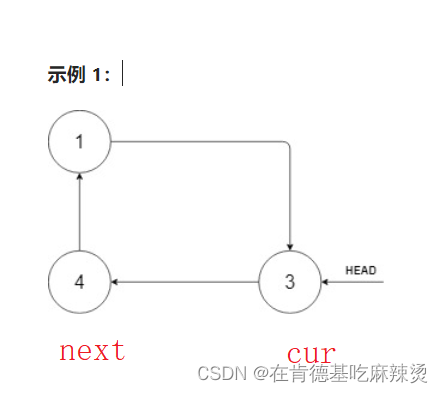
【Leetcode——排序的循环链表】
😊😊😊 文章目录一、力扣题之排序循环链表二、解题思路1. 使用双指针法2、找出最大节点,最大节点的下一个节点是最小节点,由此展开讨论总结一、力扣题之排序循环链表 题目如下:航班直达!&#…...
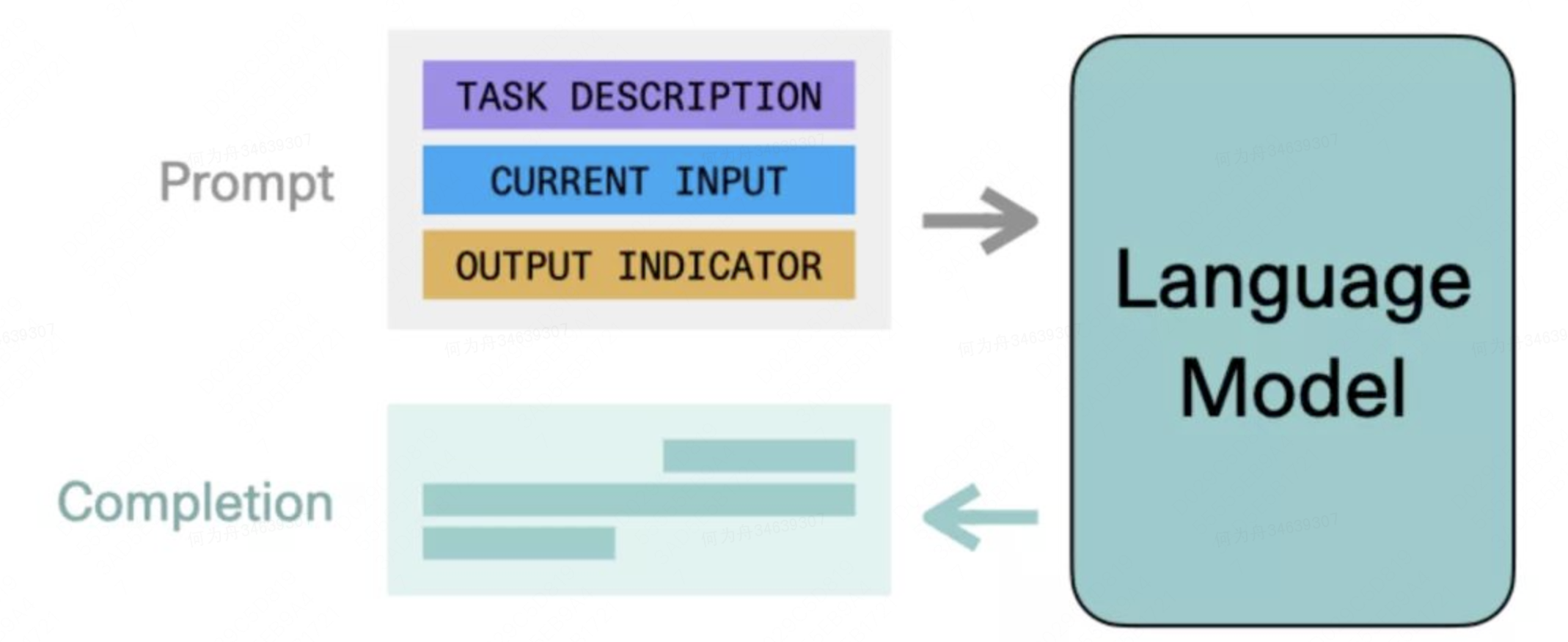
ChatGPT研究分享:机器第一次开始理解人类世界目录
0、为什么会对ChatGPT感兴趣一开始,我对ChatGPT是没什么关注的,无非就是有更大的数据集,完成了更大规模的计算,所以能够回答更多的问题。但后来了解到几个案例,开始觉得这个事情并不简单。我先分别列举出来,…...

【linux】Linux基本指令(上)
前言: 在之前我们已经简单了介绍了一下【Linux】,包括它的概念,由来啊等进行了讲解,接下来我们就将正式的踏入对其的学习!!! 本文目录👉操作系统的概念1.命令的语法1.1命令介绍1.2选…...
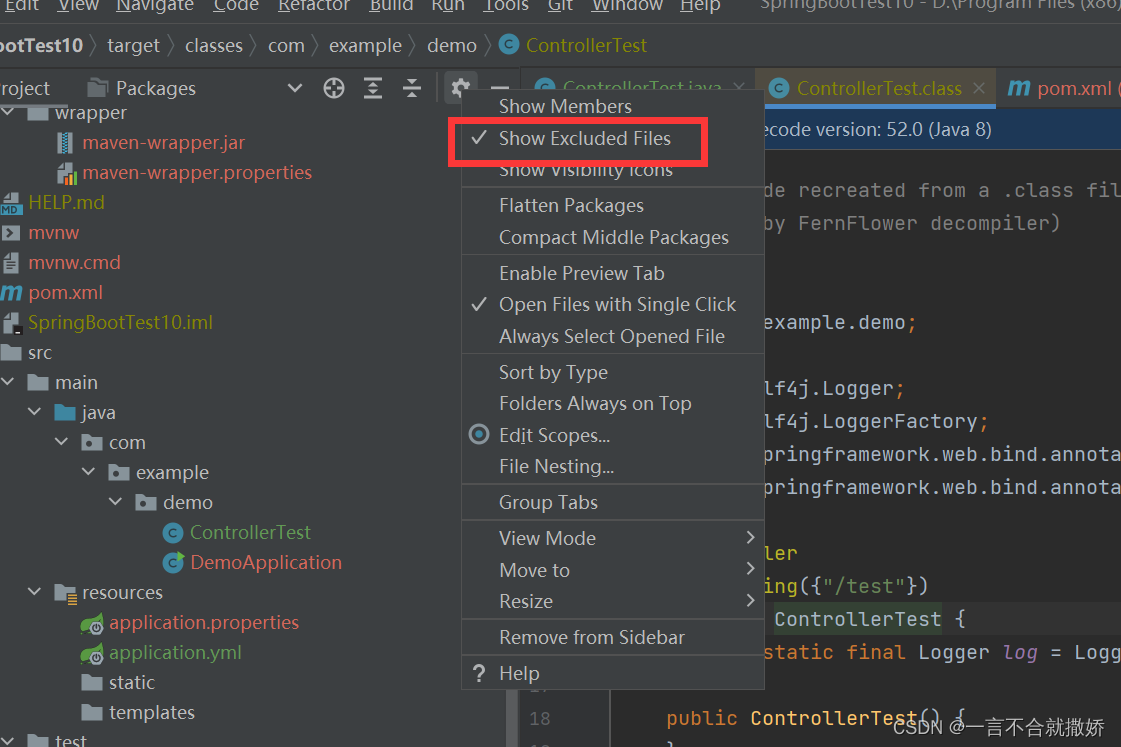
程序员必会技能—— 使用日志
目录 1、为什么要使用日志 2、自定义日志打印 2.1、在程序中得到日志对象 2.2、使用日志对象打印日志 2.3、日志格式 3、日志的级别 3.1、日志级别的分类 3.2、日志级别的设置 4、持久化日志 5、更简单的日志输出——lombok 5.1、如何在已经创建好的SpringBoot项目中添加…...
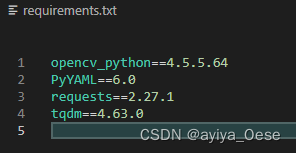
生成项目的包依赖文件requirements.txt
目录生成项目的包依赖文件requirements.txtrequirements.txt文件怎么来?使用pipreqs第三方库requirements.txt文件使用requirements.txt生成项目的包依赖文件requirements.txt 在安装部署代码时或者使用别人的项目时,会需要安装项目的依赖包,…...

安卓渐变的背景框实现
安卓渐变的背景框实现1.背景实现方法1.利用PorterDuffXfermode进行图层的混合,这是最推荐的方法,也是最有效的。2.利用canvas裁剪实现,这个方法有个缺陷,就是圆角会出现毛边,也就是锯齿。3.利用layer绘制边框1.背景 万…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...
