如何用Python求解微分方程组
文章目录
- odeint简介
- 示例
odeint简介
scipy文档中将odeint函数和ode, comples_ode这两个类称为旧API,是scipy早期使用的微分方程求解器,但由于是Fortran实现的,尽管使用起来并不方便,但速度没得说,所以有的时候还挺推荐使用的。
其中,odeint的参数如下
scipy.integrate.odeint(func, y0, t, args=(), Dfun=None, col_deriv=0, full_output=0, ml=None, mu=None, rtol=None, atol=None, tcrit=None, h0=0.0, hmax=0.0, hmin=0.0, ixpr=0, mxstep=0, mxhnil=0, mxordn=12, mxords=5, printmessg=0, tfirst=False)
其中func为待求解函数;y0为初值;t为自变量列表,其他参数都有默认选项,可以不填,而且这些参数非常多,其中常用的有
argsfunc中除了t之外的其他变量Dfunfunc的梯度函数,当此参数不为None时,若将col_deriv设为True,则可提升效率。full_output如果为True,则额外返回一个参数字典ml=None, mu=None, rtol=None, atol=None, tcrit=None, h0=0.0, hmax=0.0, hmin=0.0, ixpr=0, mxstep=0, mxhnil=0, mxordn=12, mxords=5,printmessg为True时打印信息。tfirst当为False时,func的格式为func(y,t...),否则格式为func(t, y...)
示例
对于常微分方程
θ′′(t)+bθ′(t)+csinθ(t)=0b=0.25;c=5θ(0)=π−0.1;θ′(0)=0\theta''(t)+b\theta'(t)+c\sin\theta(t)=0\\ b=0.25;\quad c=5\\ \theta(0)=\pi-0.1;\quad \theta'(0)=0 θ′′(t)+bθ′(t)+csinθ(t)=0b=0.25;c=5θ(0)=π−0.1;θ′(0)=0
将其中的二阶导数项用一个新变量替代,ω(t)=θ′(t)\omega(t)=\theta'(t)ω(t)=θ′(t),则常微分方程可拆分成微分方程组
θ′(t)=ω(t)ω′(t)=−bω(t)−csinθ(t)\begin{aligned} \theta'(t)&=\omega(t)\\ \omega'(t)&=-b\omega(t)-c\sin\theta(t) \end{aligned} θ′(t)ω′(t)=ω(t)=−bω(t)−csinθ(t)
令y=[θ,ω]y=[\theta, \omega]y=[θ,ω],则y′=[θ′,ω′]y'=[\theta', \omega']y′=[θ′,ω′],据此可设计函数func
import numpy as np
def pend(y, t, b, c):th, om = ydydt = [om, -b*om - c*np.sin(th)]return dydt
然后调用并求解
from scipy.integrate import odeint
y0 = [np.pi-0.1, 0]
t = np.linspace(0, 10, 101)
sol = odeint(pend, y0, t, args=(0.25, 5))
然后绘制一下结果
import matplotlib.pyplot as plt
plt.plot(t, sol[:,0], label="theta")
plt.plot(t, sol[:,1], label="omega")
plt.legend()
plt.show()
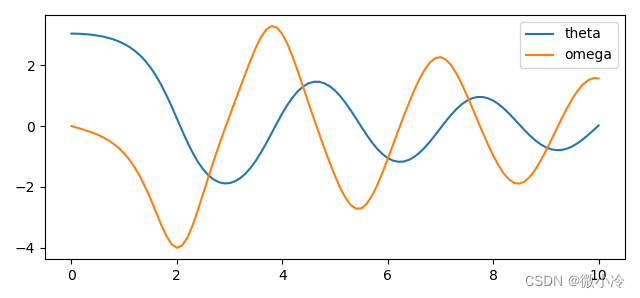
这个形状还是比较离奇的。
相关文章:

如何用Python求解微分方程组
文章目录odeint简介示例odeint简介 scipy文档中将odeint函数和ode, comples_ode这两个类称为旧API,是scipy早期使用的微分方程求解器,但由于是Fortran实现的,尽管使用起来并不方便,但速度没得说,所以有的时候还挺推荐…...

【微信小程序】-- 自定义组件 - behaviors(三十九)
💌 所属专栏:【微信小程序开发教程】 😀 作 者:我是夜阑的狗🐶 🚀 个人简介:一个正在努力学技术的CV工程师,专注基础和实战分享 ,欢迎咨询! &…...

【微信小程序】-- 自定义组件 - 父子组件之间的通信(三十八)
💌 所属专栏:【微信小程序开发教程】 😀 作 者:我是夜阑的狗🐶 🚀 个人简介:一个正在努力学技术的CV工程师,专注基础和实战分享 ,欢迎咨询! &…...

Java Web 实战 11 - 多线程进阶之常见的锁策略
常见的锁策略常见的锁策略1. 乐观锁 VS 悲观锁2. 普通的互斥锁 VS 读写锁3. 重量级锁 VS 轻量级锁4. 自旋锁 VS 挂起等待锁5. 公平锁 VS 非公平锁6. 可重入锁 vs 不可重入锁7. 常见面试题大家好 , 这篇文章给大家带来的是多线程中常见的锁策略 , 我们会给大家讲解 6 种类别的锁…...
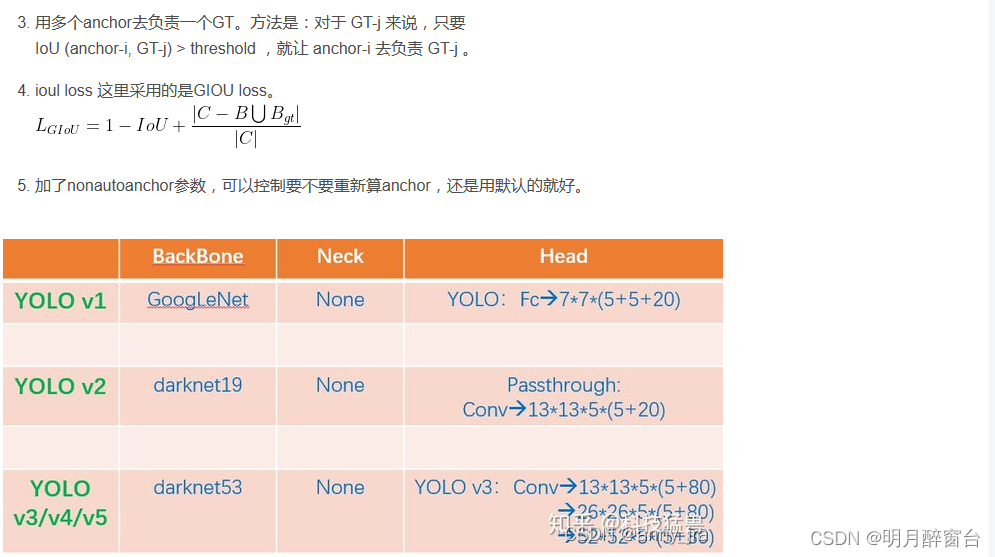
(20)目标检测算法之YOLOv5计算预选框、详解anchor计算
目标检测算法之YOLOv5计算预选框、详解anchor计算 单节段目标检测算法中:预选框的设定直接影响最终的检测精度众所周知,yolov5中采用自适应调整预选框anchor的大小,但万事开头难,配置文件config中的预设还是很重要yolo算法作为on…...
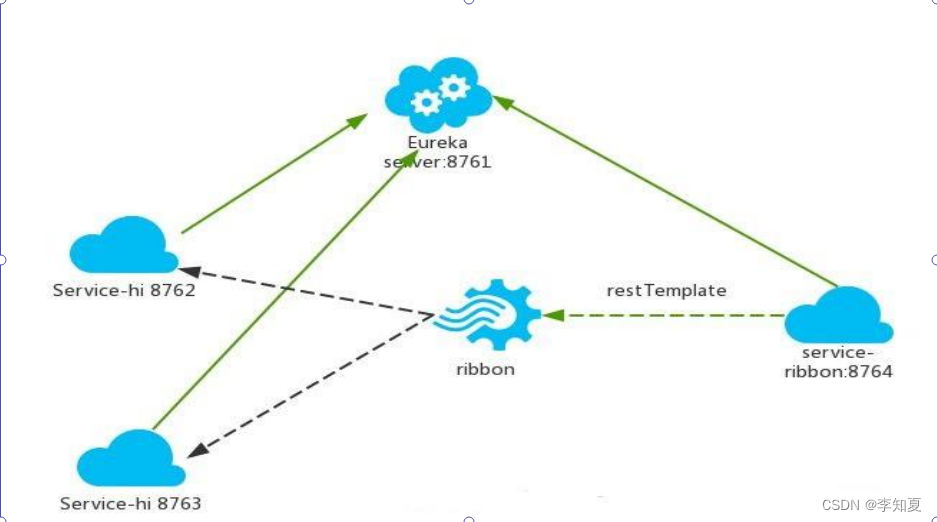
3-1 SpringCloud快速开发入门: Ribbon 是什么
接上一章节Eureka 服务注册中心自我保护机制,这里讲讲Ribbon 是什么 Ribbon 是什么 通常说的负载均衡是指将一个请求均匀地分摊到不同的节点单元上执行,负载均和分为硬件负载均衡和软件负载均衡: **硬件负载均衡:**比如 F5、深信…...
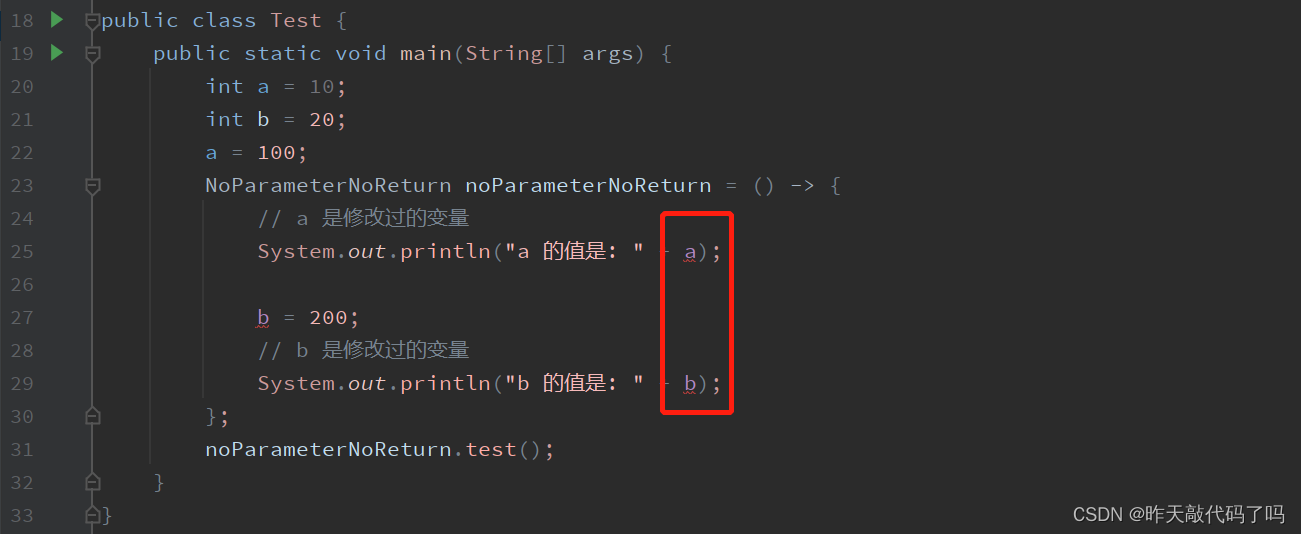
Java【lambda表达式】语法及使用方式介绍
相关文章目录 第一篇: Java【EE初阶】进程相关知识 进程管理 内存管理 文章目录相关文章目录前言一、lambda表达式 是什么?1, lambda表达式 的背景2, 什么是 函数式接口3, lambda表达式 的语法二、lambda表达式 的使用方式1, 无参无返回值2, 有一个参…...
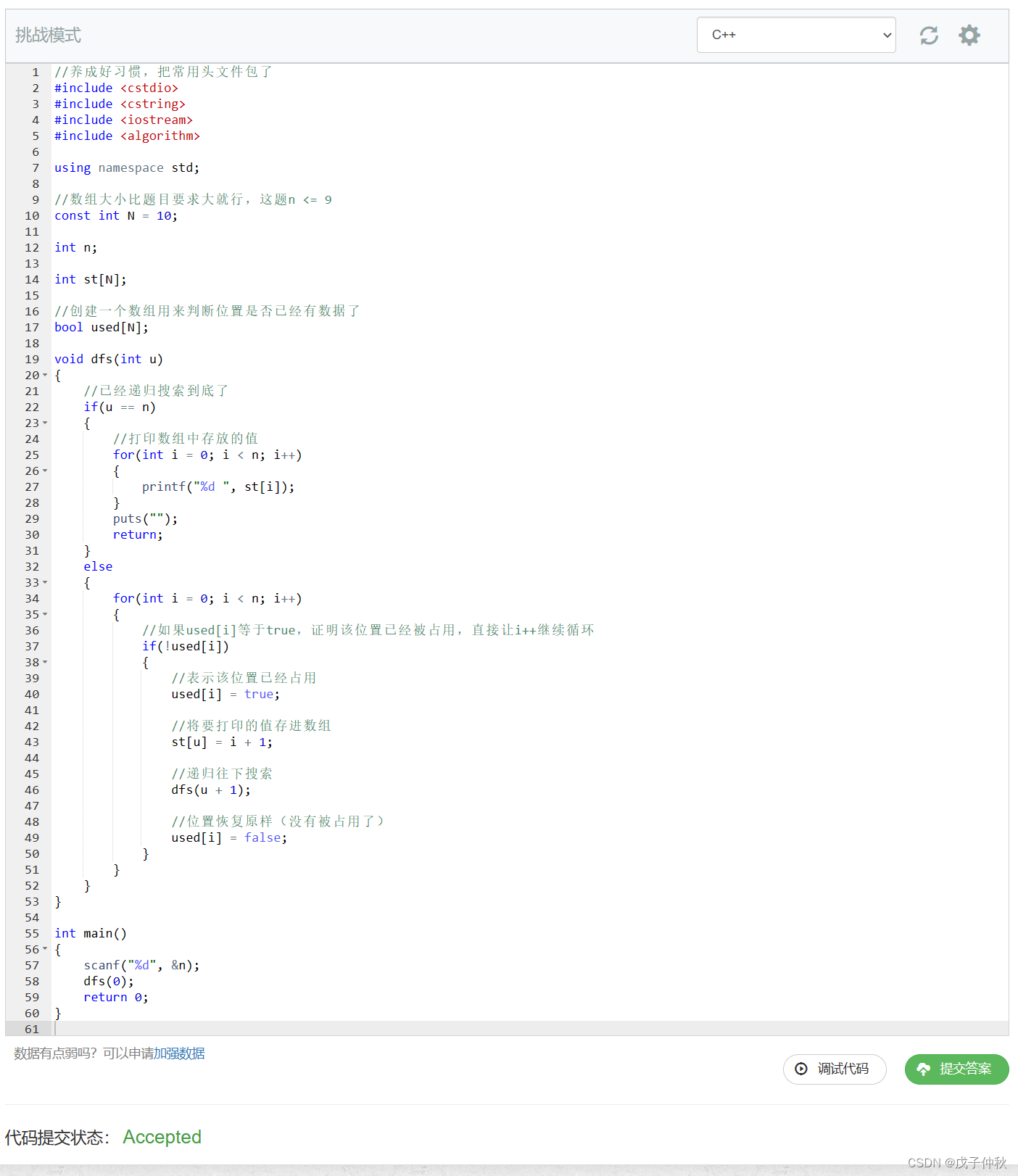
【AcWing】蓝桥杯备赛-深度优先搜索-dfs(2)
目录 写在前面: 题目:94. 递归实现排列型枚举 - AcWing题库 读题: 输入格式: 输出格式: 数据范围: 输入样例: 输出样例: 解题思路: 代码: AC &…...

‘conda‘不是内部或外部命令,也不是可运行的程序或批处理文件。
Anaconda环境搭建常见问题 conda不是内部或外部命令,也不是可运行的程序或批处理文件。 解决方案:配置环境变量 1.找到Anaconda Nvaigator单机右键 2.更多 3.打开文件所在位置 4.继续Anaconda Nvaigator单机右键,更多,选择文件…...
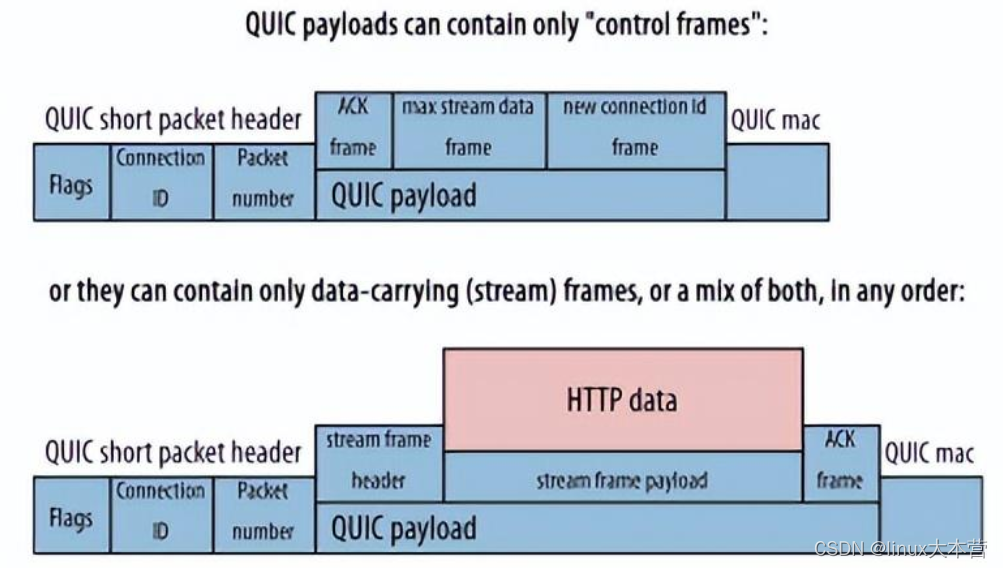
HTTP 3.0来了,UDP取代TCP成为基础协议,TCP究竟输在哪里?
TCP 是 Internet 上使用和部署最广泛的协议之一,多年来一直被视为网络基石,随着HTTP/3正式被标准化,QUIC协议成功“上位”,UDP“取代”TCP成为基础协议,TCP究竟“输”在哪里? HTTP/3 采用了谷歌多年探索的基…...

《JavaCV从入门到实战教程合集》介绍和目录
前言 《JavaCV从入门到实战教程合集》是2016年《JavaCV开发实战教程》和2018年《JavaCV入门教程》2022年《JavaCV音视频实战宝典》三合一汇总合集,完整包含JavaCV入门教程》、《JavaCV开发实战教程》系列和《JavaCV音视频实战宝典》系列所有付费内容。 《JavaCV入…...

Form Generator扩展 文本 组件
一、form-generator是什么?✨ ⭐️ 🌟 form-generator的作者是这样介绍的:Element UI表单设计及代码生成器,可将生成的代码直接运行在基于Element的vue项目中;也可导出JSON表单,使用配套的解析器将JSON解析成真实的表单。 但目前它提供的组件并不能满足我们在项目中的…...

【C/C++】必知必会知识点大总结
✍个人博客:https://blog.csdn.net/Newin2020?spm1011.2415.3001.5343 📚专栏地址:C/C知识点 📣专栏定位:整理一下 C 相关的知识点,供大家学习参考~ ❤️如果有收获的话,欢迎点赞👍…...
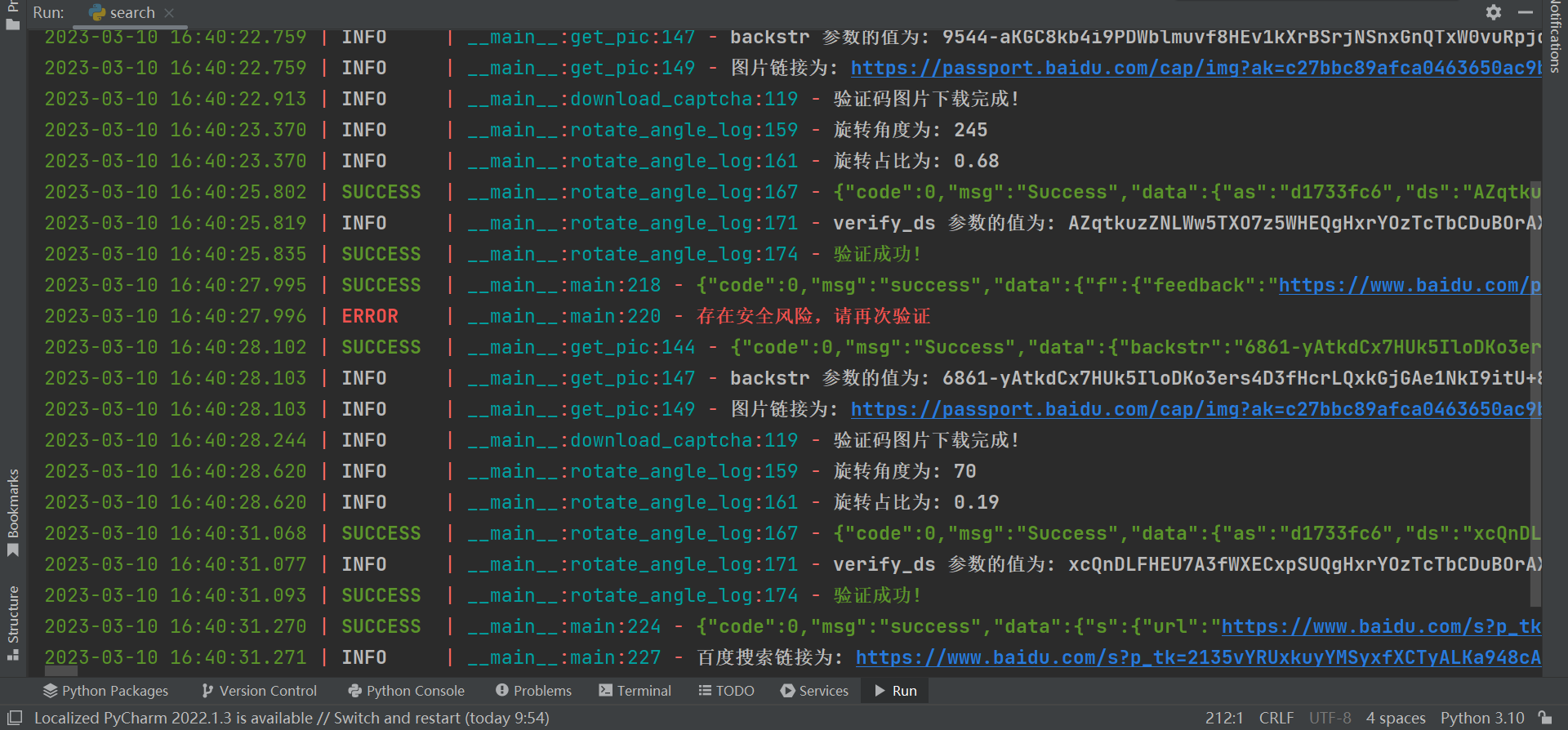
【JavaScript 逆向】百度旋转验证码逆向分析
声明本文章中所有内容仅供学习交流,相关链接做了脱敏处理,若有侵权,请联系我立即删除!案例目标爱企查百度安全验证百度搜索:aHR0cHM6Ly93YXBwYXNzLmJhaWR1LmNvbS9zdGF0aWMvY2FwdGNoYS8以上均做了脱敏处理,B…...
)
PCL 点云投影到直线(C++详细过程版)
目录 一、算法原理二、代码实现三、结果展示1、原始点云2、投影结果一、算法原理 直线方程有三种表示法:一般式、点向式、参数式。PCL中统一采用的是点向式,直线的点向式方程为: x − x 0 m = y −...
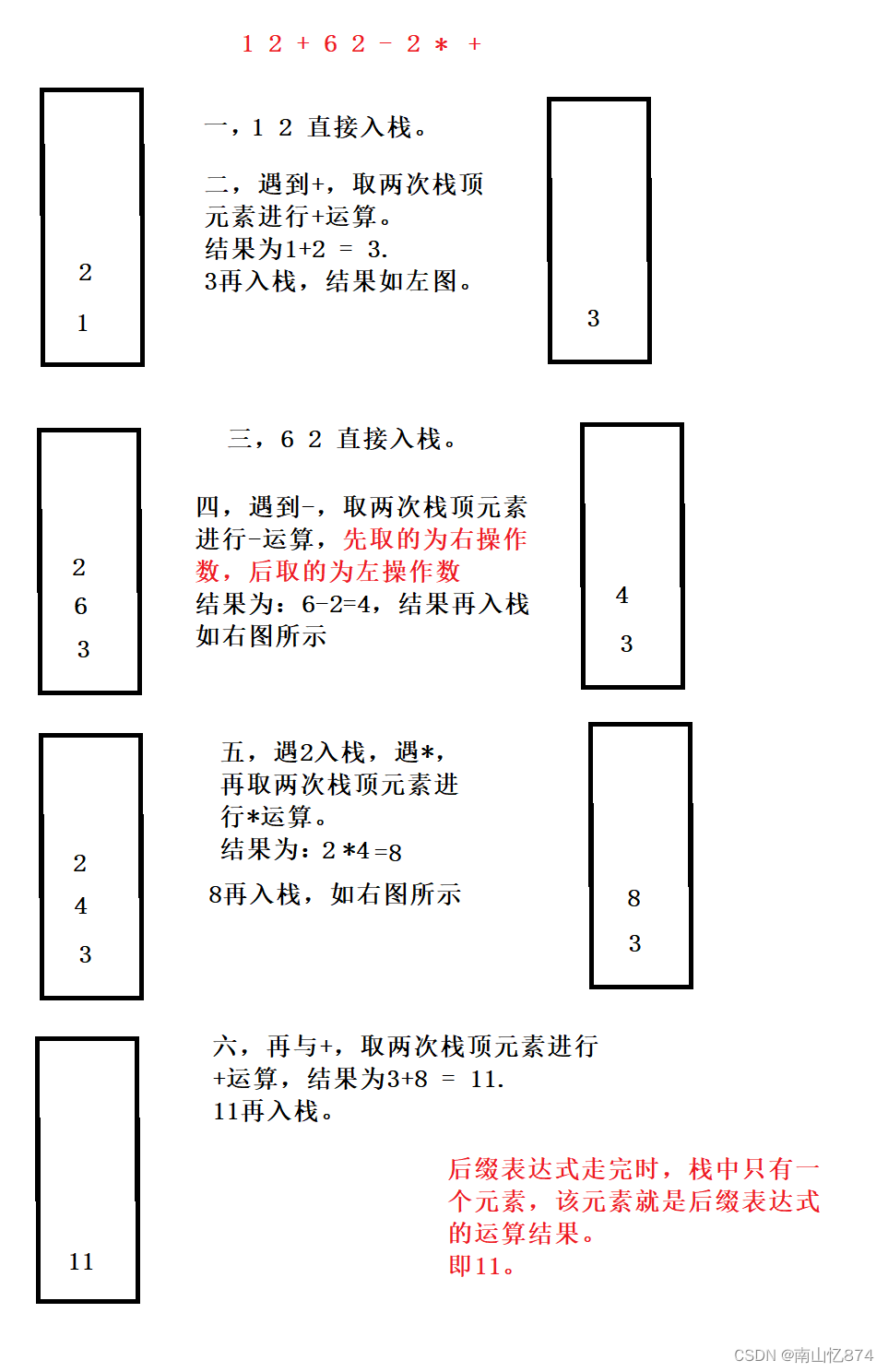
中缀表达式转后缀表示式,及后缀表达式的运算规则
后缀表达式又称为逆波兰表达式 一,中缀表达式如何转后缀表达式 假定给出以下中缀表达式 132*2-1; 要将该表达式转为后缀表达式,我们要按照一定的规则去走,并且用到栈。 先来看规则中缀转后缀的规则: 前提&#x…...

【C++】STL简介
文章目录什么是STLSTL版本 原始版本(HP版本) P.J.版本 RW版本 SGI版本STL六大组件 容器 算法 仿函数 空间配置器 迭代器 配接器STL缺陷什么是STL STL(standard template libaray-标准模板库):是C标准库的重要组成部分,不…...
文件永久存储(上)总结 python文件永久存储(创建打开文件、文件对象的各种方法及含义))
(小甲鱼python)文件永久存储(上)总结 python文件永久存储(创建打开文件、文件对象的各种方法及含义)
一、文件永久存储 如何将数据永久的存放在硬盘上,具体如下。 1.打开文件 定义:往大了讲计算机系统中由操作系统管理的具有名称的存储区域,往小了讲是生活中的PPT、Excel、word三剑客、视频文件、音频文件等。 创建打开文件: open…...

甲酸溶液除钠离子,丙酸溶液除钾离子,医药液体除钾
水是医药行业中用量大、使用 泛的一种原料,它在生产过程中和药剂药品的制备中发挥着极其重要的作用。制药用水的原水通常为自来水或深井水,原水不能直接用作制剂用水或实验用水。因为原水中含有各类盐类和化合物,溶有CO2,还存在大…...
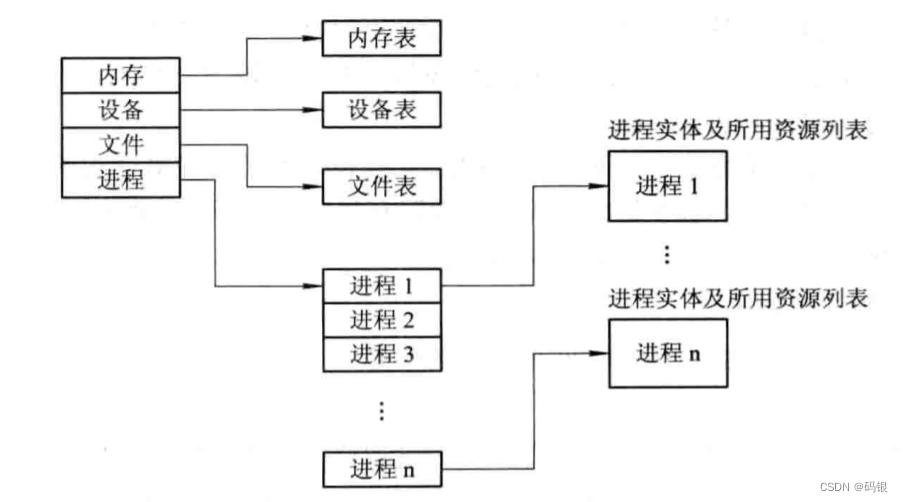
操作系统(2.2)--进程的描述与控制
目录 二、进程的描述 1.进程的定义和特征 1.1进程的定义 1.2进程的特征 2.进程的基本状态及转换 2.1进程的三种基本状态 2.2 三种基本状态的转换 2.3创建状态和中止状态 3.挂起操作和进程状态的转换 3.1 挂起状态的引入 3.2 引入挂起操作后三个进程状态的转换 …...

从“虚短虚断”到精准放大:运算放大器差分电路的设计与实战解析
1. 从“虚短虚断”说起:理想运放的两大基石 很多朋友一看到运算放大器的内部原理图就头疼,什么跨导、什么开环增益,感觉复杂得不行。其实,我们做电路设计,尤其是应用设计,很多时候可以先把运放当成一个“理…...

Maxwell Optislang的谐响应与多物理场计算在永磁电机多目标优化参数化建模及电磁振...
maxwell ,optislang 谐响应,,多物理场计算永磁电机多目标优化参数化建模电磁振动噪声仿真永磁电机的多物理场优化就像在玩一场精密的多维拼图游戏。当电磁性能、振动噪声和热特性这几个看似矛盾的指标需要同时满足时,传统单学科优…...

【ASP.NET CORE】 8. 集成 JWT 认证授权
本系列专栏基于杨中科老师的《ASP.NET Core技术内幕与项目 实战》,本人记录梳理的学习笔记,有部分的增补和省略。更全面系统的讲解,请看杨老师的视频课:【.NET教程,.Net Core视频教程,杨中科主讲】。 一、…...

人肉防火墙:用生理反应阻断黑客攻击——软件测试从业者的专业视角
在网络安全领域,传统防火墙和入侵检测系统已难以应对日益精密的黑客攻击。软件测试从业者作为系统安全的“第一道防线”,亟需创新工具来增强防御能力。本文提出“人肉防火墙”概念,即通过实时监测人体生理反应(如心率变异性、皮肤…...

UE5建模工具实战:从Lattice拉伸到法线修复的7个必学技巧
UE5建模工具实战:从Lattice拉伸到法线修复的7个必学技巧 如果你刚开始接触虚幻引擎5,或者已经从蓝图、材质系统迈入了资产制作的门槛,可能会发现一个有趣的现象:UE5内置的建模工具,远比你想象的要强大。它不再是那个只…...
报错排查与修复指南(附.env配置避坑))
ThinkPHP 5.1踩坑实录:include()报错排查与修复指南(附.env配置避坑)
ThinkPHP 5.1 深度排雷:从“空文件名”报错到配置管理的艺术 那天下午,服务器监控突然告警,一个看似普通的页面请求返回了500错误。登录服务器查看日志,一行刺眼的错误信息映入眼帘:Fatal error: Uncaught think\excep…...

聚合物与复合材料表面粗糙度测试方法的比较分析 - 综述
题目:聚合物与复合材料表面粗糙度测试方法的比较分析 - 综述 作者: Dimas Eko Prasetyo 机构: 布拉维贾亚大学机械工程系,玛琅 摘要 复合材料的发展可以与材料测试相结合,以获得复合材料的性能,如强度、硬度…...

解密Authority核心组件:Authorizer类如何掌控Rails应用权限
解密Authority核心组件:Authorizer类如何掌控Rails应用权限 【免费下载链接】authority *CURRENTLY UNMAINTAINED*. Authority helps you authorize actions in your Rails app. Its ORM-neutral and has very little fancy syntax; just group your models under o…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...
