C语言 找出一个二维数组中的鞍点
找出一个二维数组中的鞍点,即该位置上的元素在该行上最大、在该列上最小。也可能没有鞍点。
#include <stdio.h>int main() {int matrix[4][4] = {{10, 17, 13, 28},{21, 14, 16, 40},{30, 42, 23, 39},{24, 11, 19, 17}};int n = 4, m = 4;int found = 0;for (int i = 0; i < n; i++) {int max = matrix[i][0], col = 0;for (int j = 1; j < m; j++) {if (matrix[i][j] > max) {max = matrix[i][j];col = j;}}int min = matrix[0][col];for (int k = 1; k < n; k++) {if (matrix[k][col] < min) {min = matrix[k][col];}}if (max == min) {printf("鞍点: matrix[%d][%d] = %d\n", i, col, max);found = 1;}}if (!found) {printf("无鞍点\n");}return 0;
}
代码说明:
- 寻找二维数组中的鞍点,即该位置的元素在其所在行上最大,在其所在列上最小。
- 对每一行,找到最大值及其列索引,然后检查该列中是否是最小值。
- 输出所有满足条件的鞍点,如果没有则输出“无鞍点”。
相关文章:

C语言 找出一个二维数组中的鞍点
找出一个二维数组中的鞍点,即该位置上的元素在该行上最大、在该列上最小。也可能没有鞍点。 #include <stdio.h>int main() {int matrix[4][4] {{10, 17, 13, 28},{21, 14, 16, 40},{30, 42, 23, 39},{24, 11, 19, 17}};int n 4, m 4;int found 0;for (int i 0; i …...

【笔记】在linux中设置错文件如何重置
以mysql的auto.cnf文件为例...

DNS中的CNAME与A记录:为什么无法共存A解析和C解析?
在互联网的世界中,DNS(域名系统)扮演着至关重要的角色,它将易于记忆的域名转换为计算机可识别的IP地址。在这个过程中,两种常见的DNS记录类型——CNAME记录和A记录——经常被提及。然而,它们之间存在着一些…...

线程和进程
文章目录 进程和线程进程线程案例 时间片概念调度方式线程的创建和启动第一种创建方式第二种创建方式(匿名内部类)第三种创建方式(Runnable接口)main线程和t线程之间的关系 线程的名字线程的优先级线程状态 进程和线程 进程 在计…...
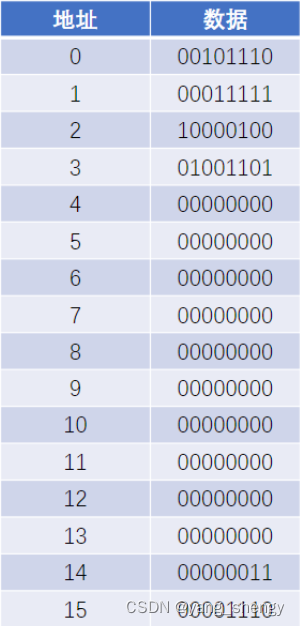
【JavaEE】 简单认识CPU
🐵本篇文章将对cpu的相关知识进行讲解 一、认识CPU 下图是简略的冯诺依曼体系结构图 上图中,存储器用来存储数据,注意在存储器中都是以二进制的形式存储数据的,CPU就是中央处理器,其功能主要是进行各种算术运算和各种…...

《数字图像处理-OpenCV/Python》第17章:图像的特征描述
《数字图像处理-OpenCV/Python》第17章:图像的特征描述 本书京东 优惠购书链接 https://item.jd.com/14098452.html 本书CSDN 独家连载专栏 https://blog.csdn.net/youcans/category_12418787.html 第17章:图像的特征描述 特征检测与匹配是计算机视觉的…...
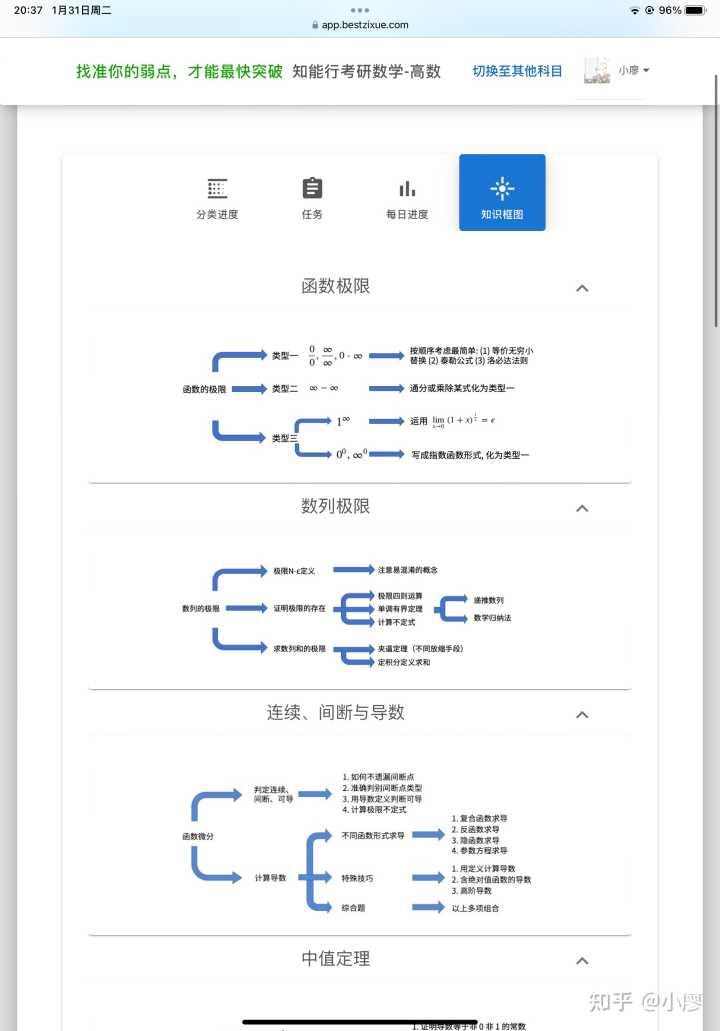
考研数学什么时候开始强化?如何保证进度不掉队?
晚了。我是实在人,不给你胡乱吹,虽然晚了,但相信我,还有的救。 实话实说,从七月中旬考研数一复习完真的有点悬,需要超级高效快速... 数二的时间也有点紧张... 中间基本没有试错的时间,让你换…...

Node.js的下载、安装和配置
天行健,君子以自强不息;地势坤,君子以厚德载物。 每个人都有惰性,但不断学习是好好生活的根本,共勉! 文章均为学习整理笔记,分享记录为主,如有错误请指正,共同学习进步。…...

java.util.Properties类介绍
java.util.Properties 是 Java 编程语言中的一个类,用于管理应用程序的配置信息,它继承自 java.util.Hashtable 类,因此它也是基于键值对的数据结构。主要用途是存储应用程序的配置参数,比如数据库连接信息、用户设置等。 以下是 Properties 类的一些主要特点和用法: 存储…...

SpringBoot后端验证码-防止密码爆破功能
一、简介 为了防止网站的用户被通过密码典爆破。引入验证码的功能是十分有必要的。而前端的验证码又仅仅是只防君子不防小人。通过burpsuit等工具很容易就会被绕过。所以后端实现的验证码才是对用户信息安全的一大重要保障。 实现思路: 1.引入图形生成的依赖 2.生成…...

ChatEval:通过多代理辩论提升LLM文本评估质量
论文地址:ChatEval: Towards Better LLM-based Evaluators through Multi-Agent Debate | OpenReviewText evaluation has historically posed significant challenges, often demanding substantial labor and time cost. With the emergence of large language models (LLMs…...

关于美国服务器IP的几个常见问题
在租用美国服务器时,与之密切相关的一个要素就是IP,关于IP的问题总是有人问起,这里列举几项常见的问题,以供参考。 一、IP收费吗? 一般情况下,在租用服务器时,会赠送几个IP,因为这些…...
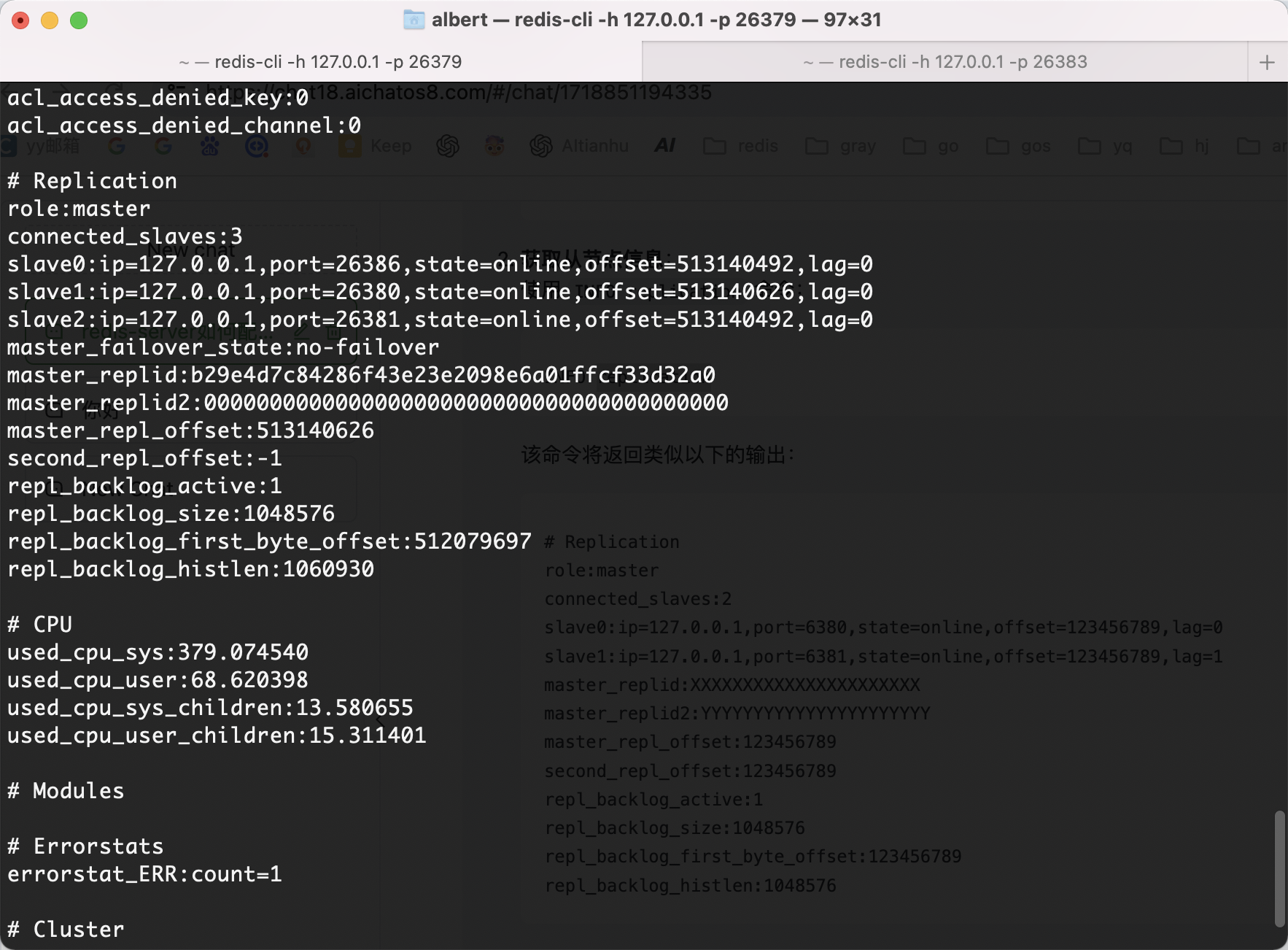
redis运维:sentinel模式如何查看所有从节点
1. 连接到sentinel redis-cli -h sentinel_host -p sentinel_port如: redis-cli -h {域名} -p 200182. 发现Redis主服务器 连接到哨兵后,我们可以使用SENTINEL get-master-addr-by-name命令来获取当前的Redis主服务器的地址。 SENTINEL get-master-a…...

价格疑云?格行WiFi创始人亲解谜团,性价比之王如何炼成?
随身wifi行业乱象频出,作为行业领跑品牌的格行随身wifi,关于价格问题一直备受质疑。关于设备上的“格行自有格行的骄傲”也被外界认定为是自大,甚至发展的线下一万多家门店也被同行不认可。近日,企业财经专访记者有幸采访了格行随…...

揭秘“消费即赚”的循环购模式
大家好,我是吴军,今天我将带您深入探索一种颠覆传统的新型商业模式——循环购模式。在这个模式中,消费者不仅能享受到购物的乐趣,还能通过消费获得实实在在的回报,甚至实现“边消费边赚钱”的奇妙体验。您是否好奇&…...

javaweb个人主页设计(html+css+js)
目录 1 前言和要求 1.1 前言 1.2 设计要求 2 预览 2.1 主页页面 2.2 个人简介 2.3 个人爱好 2.4 个人成绩有代码,但是图片已省略,可以根据自己情况添加 2.5 收藏夹 3 代码实现 3.1 主页 3.2 个人简介 3.3 个人爱好 3.4 个人成绩ÿ…...

Android常用设计模式(小白必看)
不要担心冗长,3分钟解决面试和学习问题,收藏再看 目的:当作一种模板,结合自身特点,针对项目需求来使用 目录 单例模式 特点: 实现方式: 1、饿汉式 2、线程安全的懒汉式 3、双重校验锁 使…...

swift获取app网络和本地网络权限
请求蓝牙权限: //蓝牙if #available(iOS 13.1, *) {let autostate CBManager.authorizationif(autostate .notDetermined){print("")self.manager CBCentralManager(delegate: nil, queue: DispatchQueue.main,options: [CBCentralManagerOptionShowPo…...

用LangGraph、 Ollama,构建个人的 AI Agent
如果你还记得今年的 Google I/O大会,你肯定注意到了他们今年发布的 Astra,一个人工智能体(AI Agent)。事实上,目前最新的 GPT-4o 也是个 AI Agent。 现在各大科技公司正在投入巨额资金来创建人工智能体(AI …...

ubuntu20.04系统编译yolov8-obb.cpp代码记录
任务内容 在做ncnn-yolov8-obb模型安卓端移植的过程中,对开源代码进行调试。为了确认开源代码yolov8-obb.cpp可以移植开发,先对代码进行复现。因此在linux系统下编译yolov8-obb.cpp代码,验证项目中的代码是可运行的。然后再把这个代码中的模…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...
