第241题| 确定极限中参数问题 | 武忠祥老师每日一题

解题思路:确定极限中的参数的方法是求这个极限;求极限根据类型选方法。
形可以用到三种方法:洛必达,等价,泰勒。
先观察题目,将看成一个整体,同时
,并令
,整理之后如下:
这里也要想办法弄成
的形式,例如
,在x趋于0的情况下,
,所以最终可以代换成这样:
判断类型,这同样是一个 形,在这里有两种方法来解决:
一:洛必达
,写到这一步,有人可能想到在加减法中使用等价无穷小,把-sint 换成-t来做,但是这个结论是有条件的:代换之后的数不能等价:

而这里是等价的 ,所以这里不能同价代换。接着洛必达也很麻烦,那接下来怎么做呢?
我们说:有条件要上,没有条件创造条件也要上。这里使用+t -t来构建式子。
,
分子使用泰勒展开:
;
整理得:
 ,分子两项显然不等价,可以代换。
,分子两项显然不等价,可以代换。
要想极限存在,a-1=3,a=4,答案得解。
二:泰勒公式
a=4;
前面两种是直接法,我们知道选择题还有一种方法是排除法。
三:排除法
,分子是偶函数,偶函数在0点的泰勒展开式是偶次项,不可能是奇数项。因为分母要除以一个a次项,所以a只能是偶数,排除B和D。
A选项比较好计算,先看a对不对。将a=2带入到式子中去。
(注意:这里要拆开不能直接无穷小替换,因为两个替换后的值相除极限为-1,是等价的,为什么前面不用-1+1来做,是因为这里分母的次数是2是确定的,拆开后极限依然存在,所以要拆开。)
而题目说的是极限不为0,所以A是错的,答案选C
总结知识点:
1.选择题一般是两种方法:一.直接法。二.排除法
2.该题的类型是:确定极限中的参数。
解题方法是求这个极限---求极限要根据类型选方法:
形求极限可以用到三种方法:洛必达,等价,泰勒。
3.本题使用的泰勒公式:
4.常见式子:
5.常见构建方式:+1-1。+x-x。
6.等价无穷小替换规则:

7.偶函数在0点处的泰勒展开式一定是偶次项。
相关文章:

第241题| 确定极限中参数问题 | 武忠祥老师每日一题
解题思路:确定极限中的参数的方法是求这个极限;求极限根据类型选方法。 形可以用到三种方法:洛必达,等价,泰勒。 先观察题目,将看成一个整体,同时,并令,整理之后如下: 这里也要想办…...

线程池【开发实践】
文章目录 一、为什么要用线程池1.1 单线程的问题1.2 手动创建多线程的问题1.3 线程池的作用(优点)1.4 线程池的使用场景 二、线程池的基础知识2.1 线程池的核心组件2.2 JUC中的线程池架构2.3 线程池的配置参数2.4 线程池常见的拒绝策略(可自定…...

论文辅助笔记:ST-LLM
1 时间嵌入 2 PFA(Partial Frozen Architecture) 3 ST_LLM 3.1 初始化 3.2 forward...

加入运动健康数据开放平台,共赢鸿蒙未来
HarmonyOS SDK运动健康服务(Health Service Kit)是为华为生态应用打造的基于华为帐号和用户授权的运动健康数据开放平台。在获取用户授权后,开发者可以使用运动健康服务提供的开放能力获取运动健康数据,基于多种类型数据构建运动健…...
企业化运维(7)_Zabbix企业级监控平台
官网:Zabbix :: The Enterprise-Class Open Source Network Monitoring Solution ###1.Zabbix部署### (1)zabbix安装 安装源 修改安装路径为清华镜像 [rootserver1 zabbix]# cd /etc/yum.repos.d/ [rootserver1 yum.repos.d]# vim zabbix.r…...

CTF php RCE (一)
0x01 引言 首先进入题目 应该是大部分都是一段白盒PHP审计,然后我们为了命令执行,绕过或者是钻空子等等操作,来拿到flag 0x02 基础 0x01 传参方式 这里有两个工具,hackbar和burpsuite,这两个工具非常实用 大家可以自己Googl…...

Proteus + Keil单片机仿真教程(五)多位LED数码管的静态显示
Proteus + Keil单片机仿真教程(五)多位LED数码管 上一章节讲解了单个数码管的静态和动态显示,这一章节将对多个数码管的静态显示进行学习,本章节主要难点: 1.锁存器的理解和使用; 2.多个数码管的接线封装方式; 3.Proteus 快速接头的使用。 第一个多位数码管示例 元件…...

【Linux】网络新兵连
欢迎来到 破晓的历程的 博客 ⛺️不负时光,不负己✈️ 引言 在上一篇博客中,我们简单的介绍了一些Linux网络一些比较基本的概念。本篇博客我们将开始正式学习Linux网络套接字的内容,那么我们开始吧! 1.网络中的地址管理 大家一…...

基于STM32的智能加湿器
1.简介 基于STM32的加湿器发展前景非常乐观,这主要得益于其在技术、市场需求、应用场景以及政策支持等多方面的优势。STM32微控制器具备强大的处理能力和丰富的外设接口,能够实现精确的湿度监测和智能化控制。基于STM32的加湿器可以根据环境湿度自动调节…...

ubuntu 如何解压tar
在Ubuntu中解压.tar文件,可以使用tar命令。以下是解压.tar文件的命令: tar -xvf file.tar 解释: x 表示解压 v 表示显示过程中的详细信息(可选) f 表示后面跟文件名 这将在当前目录下解压file.tar文件的内容。如果…...

C++ 算法——二分查找
如果要你在一个升序序列中查找一个值的位置,你是否还会傻乎乎的用下面这个 O ( n ) \mathcal O(n) O(n) 的代码暴力查找,如果是,我告诉你,其实根本不用这么做。 int find(int a[],int n,int k) {for(int i0;i<n;i) if(a[i]k)…...
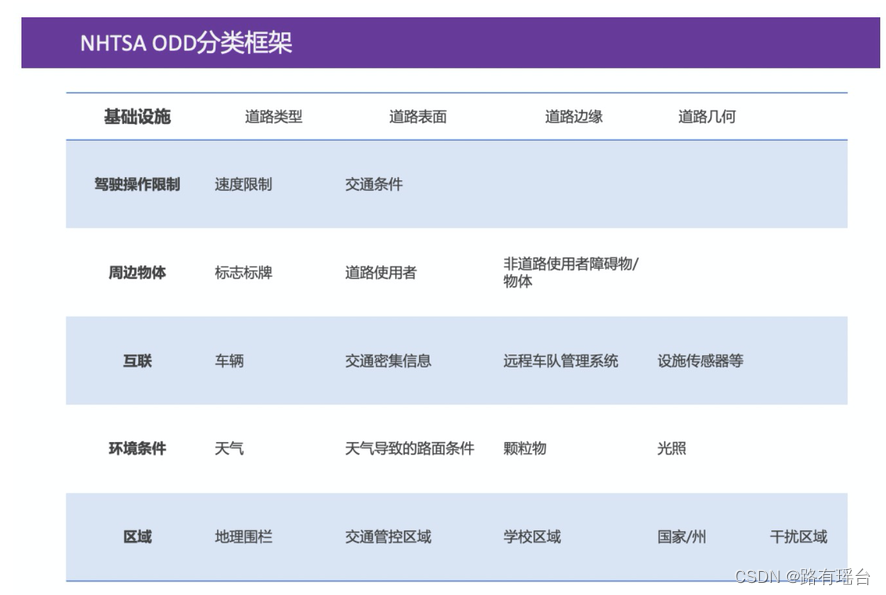
【自动驾驶仿真在做什么——初学者总结(陆续补充)】
文章目录 基础概念自动驾驶级别再稍提一下ODD是什么? 自动驾驶仿真分类软件在环仿真硬件仿真 仿真究竟难在哪?关于lidar和radar区别一些名词解释 最近也是学习自动驾驶仿真相关知识,习惯去总结一下,方便自己回顾和总结,…...

探索HTML5的设计原则:引领Web开发的未来方向
随着互联网的飞速发展,HTML5作为Web技术的核心标准之一,不仅极大地丰富了网页的表现力和交互性,还推动了Web应用向更加动态、高效、安全的方向迈进。HTML5的设计原则,体现了对用户体验、内容可访问性、跨平台兼容性以及未来可扩展…...
力扣喜刷刷--day1
1.无重复字符的最长子串 知识点:滑动窗口 基本概念 窗口:窗口是一个连续的子序列,可以是固定长度或可变长度。滑动:窗口在数据序列上移动,可以是向左或向右。边界:窗口的起始和结束位置。 应用场景 字符…...

配置linux的yum镜像为阿里镜像源
1.备份当前的yum源 mv /etc/yum.repos.d/CentOS-Base.repo /etc/yum.repos.d/CentOS-Base.repo.backup 2.下载新的CentOS-Base.repo 到/etc/yum.repos.d wget -O /etc/yum.repos.d/CentOS-Base.repo http://mirrors.aliyun.com/repo/Centos-7.repo 3.清空并生成缓存 yum clean …...

react使用markdown进行展示
有一些文档非常长,但是又要挨个设置样式,直接用 组件库 - marked 注意文档要放在public下才能读取。但非常方便 import { marked, Renderer } from "marked".....const [html, setHtml] useState<any>("")const renderer:…...

实时温湿度监测系统:Micropython编码ESP32与DHT22模块的无线数据传输与PC端接收项目
实时温湿度监测系统 前言项目目的项目材料项目步骤模拟ESP32接线连接测试搭建PC端ESP32拷录环境对ESP32进行拷录PC端搭建桌面组件本地数据接收桌面小组件部分 实验总结 前言 人生苦短,我用Python。 由于我在日常工作中经常使用Python,因此在进行该项目…...

CloudWatch Logs Insights 详解
CloudWatch Logs Insights 是 AWS 提供的强大日志分析工具,允许您快速、交互式地搜索和分析日志数据。本文将详细介绍使用 CloudWatch Logs Insights 所需的权限、常用查询方法,以及一些实用的查询示例。 1. 所需权限 要使用 CloudWatch Logs Insights,用户需要具备以下 I…...
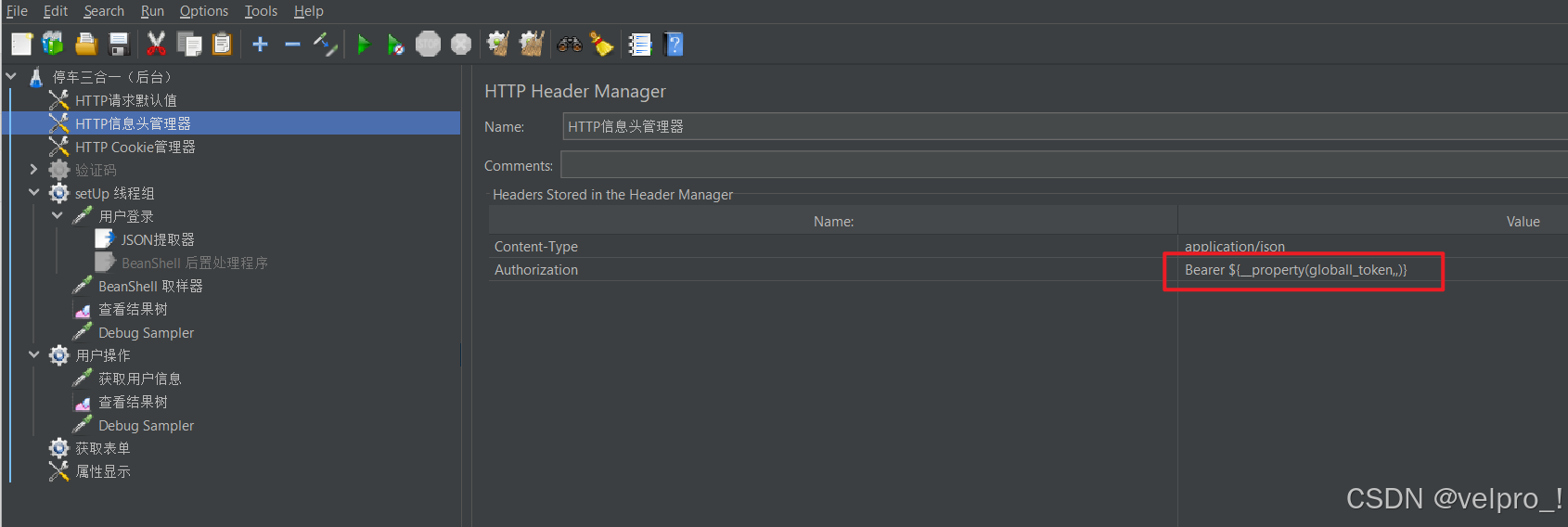
Jmeter在信息头中设置Bearer与 token 的拼接值
思路:先获取token,将token设置成全局变量,再与Bearer拼接。 第一步:使用提取器将token值提取出来,使用setProperty函数将提取的token值设置成全局变量,在登录请求后面添加BeanShell取样器 或者 BeanShell后…...

C#程序调用Sql Server存储过程异常处理:调用存储过程后不返回、不抛异常的解决方案
目录 一、代码解析: 二、解决方案 1、增加日志记录 2、异步操作 注意事项 3、增加超时机制 4、使用线程池 5、使用信号量或事件 6、监控数据库连接状态 在C#程序操作Sql Server数据库的实际应用中,若异常就会抛出异常,我们还能找到异…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...
