量化交易策略:赌徒在股市会运用凯利公式(附python代码)
一、凯利公式的历史
凯利公式(Kelly Criterion)是由美国贝尔实验室物理学家约翰·拉里·凯利(John Larry Kelly)于1956年提出的,用于计算最优投资比例的一种数学公式。凯利公式的核心思想是:在期望收益和风险之间找到一个平衡点,使得投资者在承担一定风险的情况下,能够获得最大化的收益,后来被广泛应用于投资领域,特别是股票量化交易策略中。
凯利公式的提出,为投资者提供了一个科学的决策依据,使得投资者在面对不确定性时,能够更加理性地进行投资决策。自凯利公式问世以来,被无数投资者所推崇。
二、凯利公式的原理
凯利公式的数学表达式为:
f = (bp - q) / b
其中,f表示最优投资比例,b表示赔率,p表示获胜概率,q表示失败概率。
凯利公式的应用,可以帮助投资者在面对多个投资品种时,合理地分配资金,以实现最大化的收益。通过凯利公式,投资者可以计算出每个投资品种应该投入的资金比例,从而在不确定的市场环境中,做出最佳的投资决策。
三、凯利公式的Python代码实现
先导入所需的库:
import numpy as np
接下来,定义一个函数来计算赔率、获胜概率和失败概率:
相关文章:
)
量化交易策略:赌徒在股市会运用凯利公式(附python代码)
一、凯利公式的历史 凯利公式(Kelly Criterion)是由美国贝尔实验室物理学家约翰拉里凯利(John Larry Kelly)于1956年提出的,用于计算最优投资比例的一种数学公式。凯利公式的核心思想是:在期望收益和风险之间找到一个平衡点,使得投资者在承担一定风险的情况下,能够获得…...
)
信息系统项目管理师【一】英文选择题词汇大全(1)
一、计算机相关词汇 数据挖掘 Data Mining分布式计算 Distributed Computing云计算 Cloud Computing物联网 IOT Internet of Things大数据 Big Data人工智能 artificial intelligence互联网 Internet plus区块链 Blockchain5G 5th-Generation感知层 sensing layer机器学习 mac…...

怎么判断自己是否适合学习PMP?
判断自己是否适合学习PMP项目管理专业人士认证,可以从以下几个方面进行考量: 1、职业发展需求: 如果您在项目管理领域工作,或计划未来从事相关工作,PMP认证能显著提升您的竞争力。 对于项目经理、产品经理、技术领导…...

最新的数据防泄密方案来袭!
沙箱技术作为一种先进的数据安全解决方案,在数据防泄密领域发挥着日益重要的作用。它通过构建一个隔离的虚拟环境,使得应用程序在该环境中运行,从而隔离了应用程序对系统资源的直接访问,有效防止了数据泄露的风险。 一、沙箱技术在…...

Python数据处理之高效校验各种空值技巧详解
概要 在编程中,处理空值是一个常见且重要的任务。空值可能会导致程序异常,因此在进行数据处理时,必须确保数据的有效性。Python 提供了多种方法来处理不同数据对象的空值校验。本文将详细介绍如何对Python中的各种数据对象进行空值校验,并包含相应的示例代码,帮助全面掌握…...

Spring Boot与RSocket的集成
Spring Boot与RSocket的集成 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿! 一、引言 RSocket是一个基于异步、消息驱动的网络协议,旨在解决微服…...

UI Toolkit generateVisualContent的使用
方法描述: Called when the VisualElement visual contents need to be (re)generated. When this delegate is handled, you can generate custom geometry in the content region of the VisualElement. For an example, see the MeshGenerationContext documentation. This…...
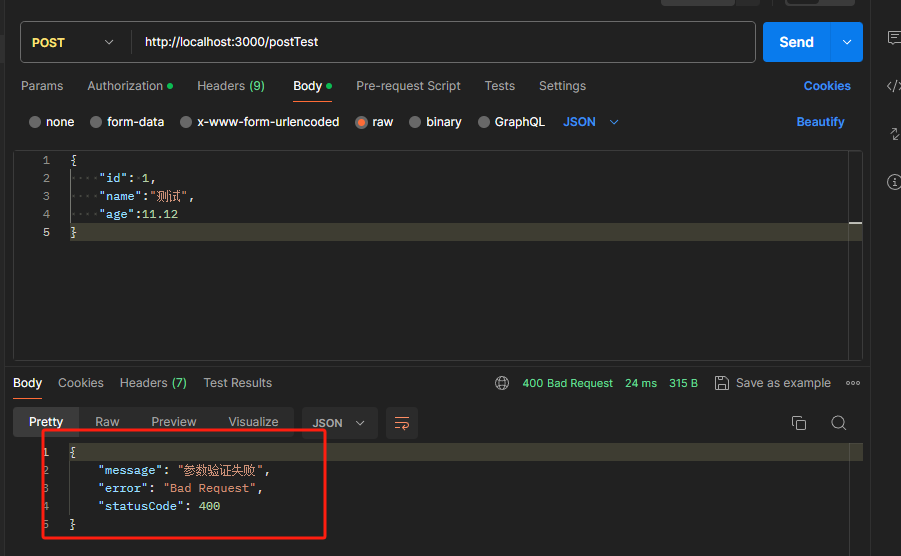
第十六章 ValidationPipe验证post请求参数
在此之前我们用到的请求都是get请求,接下来我们使用post 请求 并接收参数,通过 Body 装饰器来取注意:post请求带参数 我们通过游览器路径是直接请求不了的 需要使用postman 来发 post 请求postman 下载网站 https://www.postman.com/download…...

HippoRAG如何从大脑获取线索以改进LLM检索
知识存储和检索正在成为大型语言模型(LLM)应用的重要组成部分。虽然检索增强生成(RAG)在该领域取得了巨大进步,但一些局限性仍然没有克服。 俄亥俄州立大学和斯坦福大学的研究团队推出了HippoRAG,这是一种创新性的检索框架,其设计理念源于人类…...
求函数最小值-torch版
目标:torch实现下面链接中的梯度下降法 先计算 的导函数 ,然后计算导函数 在处的梯度 (导数) 让 沿着 梯度的负方向移动, 自变量 的更新过程如下 torch代码实现如下 import torchx torch.tensor([7.5],requires_gradTrue) # print(x.gr…...

如何将HEVC格式的视频转换为无损、未压缩的MP4格式视频?
在和大家分享视频格式转换之前,先跟大家分享一下HEVC格式的视频到底是什么文件?压缩原理是什么?了解了它的本质之后,我们就可以知道如何保证视频高清无损了。 如何将HEVC格式的视频转换为无损、未压缩的MP4格式视频? …...

自定义在线活动报名表单小程序源码系统 源代码+搭建部署教程 可二次定制开发
系统概述 在数字化时代,线上活动成为连接用户与组织的重要桥梁。为了高效地管理活动报名流程,一款灵活、易用的在线活动报名表单小程序显得尤为重要。本文旨在为开发者提供一套全面的解决方案,包括自定义在线活动报名表单小程序的源代码分析…...

数据分析入门指南:表结构数据(三)
在数字化转型的浪潮中,表结构数据作为企业决策支持系统的核心要素,其重要性日益凸显。本文深入剖析了表结构数据的本质特征、高效处理策略,并探讨了其在现代商业智能环境中的广泛应用,旨在为数据分析师与决策者提供前沿洞察与实战…...

凌凯科技前五大客户依赖症加剧:研发费用率骤降,应收账款大增
《港湾商业观察》黄懿 6月13日,上海凌凯科技股份有限公司(下称“凌凯科技”)在港交所提交上市申请,拟于主板上市,华泰国际为其独家保荐人。 凌凯科技致力于提供小分子化合物技术和产品解决方案,专注于制药…...

5 科大讯飞AI大赛:热力学定律的电池材料生产参数动态调控
赛题名称:基于热力学定律的电池材料生产参数动态调控挑战赛 赛题类型:数据挖掘 赛题任务:利用时空模型进行建模并预测匣钵实际温度 赛题链接:https://challenge.xfyun.cn/topic/info?typebattery-material&optiontjjg&…...

概论(二)随机变量
1.名词解释 1.1 样本空间 一次具体实验中所有可能出现的结果,构成一个样本空间。 1.2 随机变量 把结果抽象成数值,结果和数值的对应关系就形成了随机变量X。例如把抛一次硬币的结果,正面记为1,反面记为0。有变量相对应的就有自…...

Apache AGE 安装部署
AGE概述 概述 我们可以通过源码安装、拉取docker镜像运行、直接使用公有云三种方式中的任意一种来使用Apache AGE 获取 AGE 发布版本 可以在 https://github.com/apache/age/releases 找到发布版本和发布说明。 源代码 源代码可以在 https://github.com/apache/age 找到…...
Python29 Tensorflow的基本知识和使用
1. TensorFlow TensorFlow 是一个开源的机器学习框架,由 Google Brain 团队开发。它用于数据流图的计算,尤其擅长深度学习任务。在 TensorFlow 中,数据流图(Data Flow Graph)是其核心概念之一,它定义了计算…...

Linux操作系统上用到的磁盘分区管理工具
parted磁盘分区工具 磁盘格式:MBR, GPT, 这两种名称分别是硬盘里面分区表两种格式的称呼, 第一种MBR格式的分区表最大支持2TB的容量, 磁盘的三种分区主分区,扩展分区,逻辑分区,主分区扩展分区<4 第…...

Python数据结构的库之Fuk使用详解
概要 fuk 是一个用于处理 Python 数据结构的库,全称为 "Fast and Uncomplicated Kit"。它提供了一系列高效、简洁的数据结构实现,以及对 Python 内置数据结构的扩展。通过使用 fuk,开发者可以更加方便地处理列表、集合、字典等数据类型,提高代码的执行效率和可读…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...
