docker笔记2
docker笔记2
- 一、阿里云镜像配置
- 二、docker基本原理
- 1.docker是如何启动一个容器的
- 2.docker的底层原理
- 三、镜像命令
- 总结
一、阿里云镜像配置
配置镜像的目的
- 由于Docker Hub等公共镜像仓库的服务器可能位于国外,直接从中拉取镜像时可能会遇到网络延迟或不稳定的问题,导致下载速度缓慢甚至失败。
具体使用
- 阿里云镜像服务拥有遍布全国的节点,用户可以选择离自己最近的节点来加速镜像的下载,从而显著提高镜像的拉取速度
在阿里云官网找到容器镜像服务下的镜像加速器,在加速器下选择CentOS系统,然后便可以根据提示的命令配置阿里云镜像。
sudo mkdir -p /etc/docker
sudo tee /etc/docker/daemon.json <<-'EOF'
{"registry-mirrors": ["https://kl4flq2i.mirror.aliyuncs.com"]
}
EOF
sudo systemctl daemon-reload
sudo systemctl restart docker
二、docker基本原理
1.docker是如何启动一个容器的
下图为docker启动一个镜像的流程图。首先docker会在本地寻找该镜像是否存在,如果不存在,会去访问docker hub;如果docker hub存在该镜像,那么会下载到本地,使用该镜像构建容器执行;如果docker hub中没有该镜像,那么报错,找不到镜像。

2.docker的底层原理
再来看下这个对比图,docker直接使用操作系统内核,而不是像虚拟机部署那样分别在每个虚拟上安装操作系统,这避免了安装的繁琐,同时也加快了运行的速度。

下图可以看到,客户端都是通过后台的守护进程来操作docker容器的。
Docker是一个Client-Server结构的系统,Docker的守护进程运行在主机上,通过Socket从客户端访问!
DockerServer接收到Docker-Client的指令,就会执行这个命令。

三、镜像命令
帮助命令
docker version # 显示docker的版本信息
docker info # 显示docker的系统信息,包括镜像和容器的数量
docker 命令 --help # 帮助命令
查看镜像
docker images

搜索镜像
docker search mysql
比如我这里搜索mysql镜像,那么就会到浏览器查找镜像,并安装stars降序排列,stars越多,说明使用的人越多。

下载镜像
docker pull mysql
下面是我下载镜像,这个下载有些类似分片上传的感觉。如果你下载不同的版本,那么docker只会下载非重复的内容。

删除镜像
# 删除指定镜像
docker rmi -f IMAGE ID
# 删除多个镜像
docker rmi -f IMAGE ID1 IMAGE ID2 IMAGE ID3
# 删除全部镜像
docker rmi -f $(docker images -aq)
总结
简单记录docker的基本原理和基本命令,最重要的还是操作。
相关文章:

docker笔记2
docker笔记2 一、阿里云镜像配置二、docker基本原理1.docker是如何启动一个容器的2.docker的底层原理 三、镜像命令总结 一、阿里云镜像配置 配置镜像的目的 由于Docker Hub等公共镜像仓库的服务器可能位于国外,直接从中拉取镜像时可能会遇到网络延迟或不稳定的问…...

数字统计
import java.util.Scanner;// 注意类名必须为 Main, 不要有任何 package xxx 信息 public class Main {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别// 注意 while 处理多个 caseint a in.nextInt();i…...

Git 使用问题
Git 使用问题 1, 网络问题 1, 网络问题 # 报错如下: fatal: unable to access https://github.com/xianglingliwei/HRNet.git/: Failed to connect to github.com port 443 after 21044 ms: Couldnt connect to server在不能正常访问Github的区域,需要设…...

JMH325【剑侠情缘3】第2版80级橙武网游单机更稳定亲测视频安装教学更新整合收集各类修改教学补丁兴趣可以慢慢探索
资源介绍: 是否需要虚拟机:是 文件大小:压缩包约14G 支持系统:win10、win11 硬件需求:运行内存8G 4核及以上CPU独立显卡 下载方式:百度网盘 任务修复: 1,掌门任务(…...

大数据专业创新人才培养体系的探索与实践
一、引言 随着大数据技术的迅猛发展,其在各行各业中的应用日益广泛,对大数据专业人才的需求也日益增长。我国高度重视大数据产业的发展,将大数据作为国家战略资源,推动大数据与各行业的深度融合。教育部也积极响应国家战略&#…...

MySQL 中的 DDL、DML、DQL 和 DCL
文章目录 1. 数据定义语言(DDL)2. 数据操作语言(DML)3. 数据查询语言(DQL)4. 数据控制语言(DCL)总结 在 MySQL 数据库管理系统中,SQL 语句可以根据其功能分为不同的类别&…...

基础架构服务API:降低成本,提升业务效益
基础架构服务API的应用可以显著降低企业的成本,并提升业务效益。通过使用这些API,企业可以充分利用云计算、自动化部署和资源管理等功能,从而减少了传统基础设施所需的大量投资和维护成本。这些API还提供了弹性扩展和自动化功能,使…...
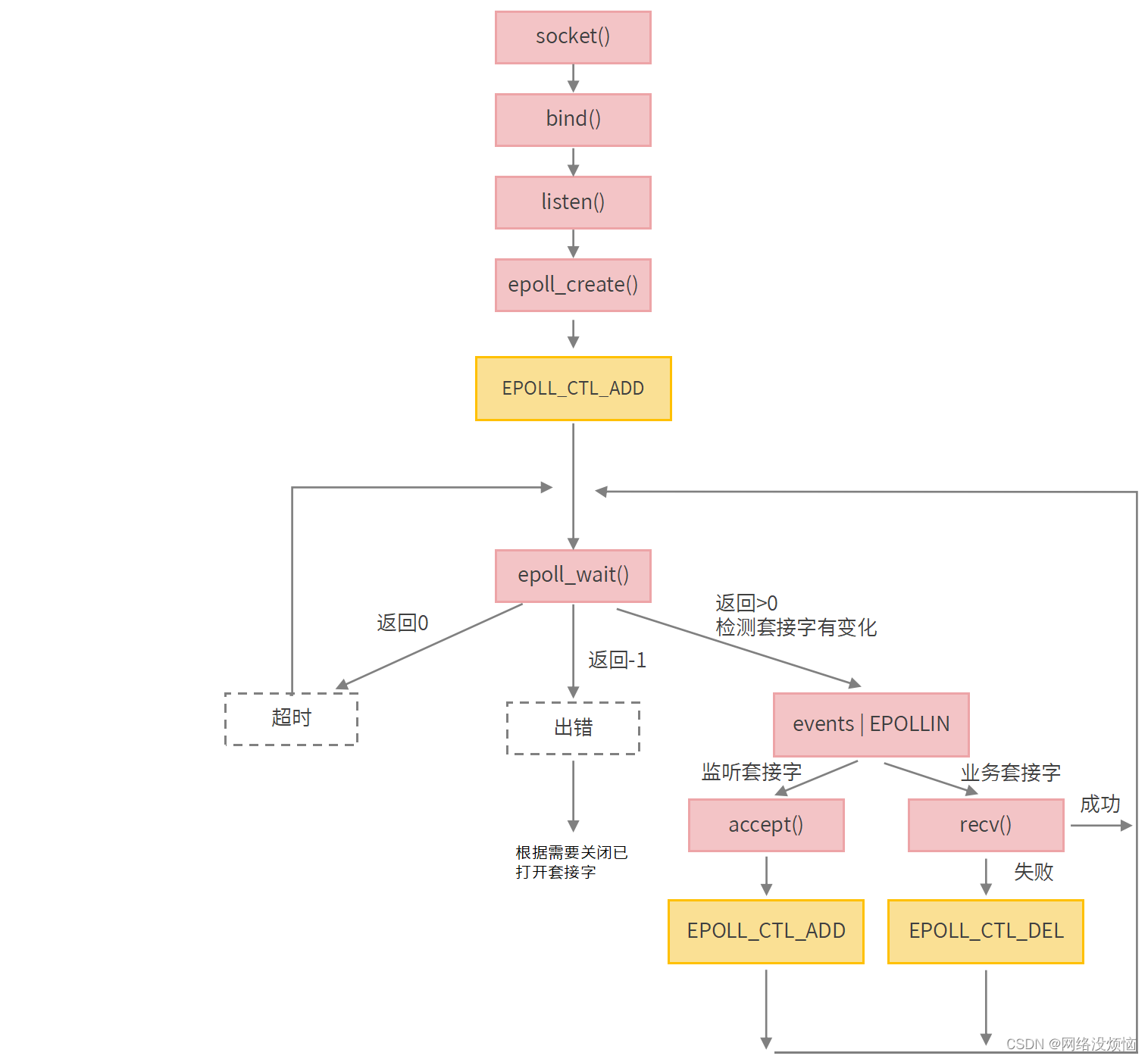
Redis IO多路复用
0、前言 本文所有代码可见 > 【gitee code demo】 本文涉及的主题: 1、BIO、NIO的业务实践和缺陷 2、Redis IO多路复用:redis快的主要原因 3、epoll 架构 部分图片 via 【epoll 原理分析】 1、BIO单线程版 1.1 业务代码 client client代码相同…...

如何在Vue中实现拖拽功能?
Vue.js是一款流行的JavaScript框架,用于构建用户界面。其中一个常见的需求是在Vue中实现拖拽功能,让用户可以通过拖拽元素来进行交互。今天,我们就来学习如何在Vue中实现这一功能。 首先,我们需要明白拖拽功能的基本原理…...

在Linux下使用Docker部署chirpstack
目录 一、前言 二、chirpstack 1、chirpstack是什么 2、chirpstack组件 3、为什么选择Docker部署 三、Linux下部署过程 四、web界面部署过程 一、前言 本篇文章我是在Linux下使用 Docker 进行部署chirpstack,chirpstack采用的是v4 版本,v4 版本 与…...

《昇思25天学习打卡营第14天|计算机视觉-ShuffleNet图像分类》
FCN图像语义分割&ResNet50迁移学习&ResNet50图像分类 当前案例不支持在GPU设备上静态图模式运行,其他模式运行皆支持。 ShuffleNet网络介绍 ShuffleNetV1是旷视科技提出的一种计算高效的CNN模型,和MobileNet, SqueezeNet等一样主要应用在移动端…...

将字符串写入结构体变量中
将字符串写入结构体变量中,主要涉及到结构体中字符数组(或指针)的使用。 一、使用字符数组 假设你有一个结构体,它包含一个字符数组来存储字符串: #include <stdio.h> #include <string.h> // 用于st…...

iPhone 16 Pro系列将标配潜望镜头:已开始生产,支持5倍变焦
ChatGPT狂飙160天,世界已经不是之前的样子。 更多资源欢迎关注 7月6日消息,据DigiTimes最新报道,苹果将在iPhone 16 Pro中引入iPhone 15 Pro Max同款5倍光学变焦四棱镜潜望镜头。 报道称,目前苹果已经将模组订单交至大立光电和玉…...

PG在还没有pg_class的时候怎么访问基础系统表?
在没有pg_class的时候,数据库怎么访问系统表?这个问题可以分成两个阶段来看: 数据库簇初始化,此时一个database都没有,所以怎么构造和访问pg_class等系统表是一个问题私有内存初始化系统表。PG的系统表信息是放在back…...

UnityHub 无法添加模块问题
文章目录 1.问题描述2.问题解决 1.问题描述 在Hub中无法添加模块 2.问题解决 1、点击设置 2、设置版本安装位置 可以发现installs的安装位置路径设置不是unity安装位置,这里我们更改成自己电脑unity安装位置的上一级路径 添加模块正常:...

python04——类(基础new)
类其实也是一种封装的思想,类就是把变量、方法等封装在一起,然后可以通过不同的实例化对其进行调用操作。 1.类的定义 class 类名: 变量a def __init__ (self,参数2,参数2...):初始化函数!!&…...
聚合2、递归)
【Python百日进阶-Web开发-Peewee】Day296 - 查询示例(五)聚合2、递归
文章目录 14.6.13 列出每个指定设施的预订总小时数 List the total hours booked per named facility14.6.14 列出每位会员在 2012 年 9 月 1 日之后的首次预订 List each member’s first booking after September 1st 201214.6.15 生成成员名称列表,每行包含成员总数 Produc…...

闲话银行家舍入法,以及在程序中如何实现
前言 相信对于四舍五入的舍入法,大家都耳熟能详,但对于银行家舍入法,可能就会比较少接触了! 可是在金融界,银行家舍入法可是大名鼎鼎的主角之一,主要应用于金融领域和涉及货币计算的场合。 那么…...
)
最短路径算法(算法篇)
算法之最短路径算法 最短路径算法 概念: 考查最短路径问题,可能会输入一个赋权图(也就是边带有权的图),则一条路径的v1v2…vN的值就是对路径的边的权求和,这叫做赋权路径长,如果是无权路径长就是单纯的路径上的边数。…...

昇思25天学习打卡营第11天 | LLM原理和实践:基于MindSpore实现BERT对话情绪识别
1. 基于MindSpore实现BERT对话情绪识别 1.1 环境配置 # 实验环境已经预装了mindspore2.2.14,如需更换mindspore版本,可更改下面mindspore的版本号 !pip uninstall mindspore -y !pip install -i https://pypi.mirrors.ustc.edu.cn/simple mindspore2.2…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...

TJCTF 2025
还以为是天津的。这个比较容易,虽然绕了点弯,可还是把CP AK了,不过我会的别人也会,还是没啥名次。记录一下吧。 Crypto bacon-bits with open(flag.txt) as f: flag f.read().strip() with open(text.txt) as t: text t.read…...

2025年- H71-Lc179--39.组合总和(回溯,组合)--Java版
1.题目描述 2.思路 当前的元素可以重复使用。 (1)确定回溯算法函数的参数和返回值(一般是void类型) (2)因为是用递归实现的,所以我们要确定终止条件 (3)单层搜索逻辑 二…...
