染色法判定二分图
什么是二分图?
二分图,也称作二部图,是图论中的一种特殊模型。在一个无向图G=(V,E) 中,如果顶点集合 V 可以被分割成两个互不相交的子集 A 和 B,并且图中的每条边 (i,j) 关联的两个顶点 i 和 j 分别属于这两个不同的顶点集(即 i 属于 A,j 属于 B),那么这样的图 G 就被称为二分图。二分图有一些特殊的性质和应用,例如,二分图中不存在奇数长度的环,并且它可以用在匹配问题、网络流问题等不同领域。
也就是说:二分图,就是可以使用两种不同的颜色对图中的顶点进行均匀染色的图,例如:存在两个区域A、B,A与B之间可以通过边进行连接,但是A与B内部是没有边的。
二分图,当且仅当图中不含奇数环。如果存在奇数环,那么就一定不是二分图。因为图中不含奇数环,所以染色过程中一定没有矛盾
图示:图中1和2表示不同的颜色,即二分图里一条边上的两个点的颜色是不尽相同的

题目:860. 染色法判定二分图 - AcWing题库

代码:
#include<iostream>
#include<cstring>
#include<algorithm>using namespace std;const int N=1e5+10,M=2*N;
int e[M],h[N],ne[M],idx;
int n,m,color[N];void add(int a,int b)
{e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}bool dfs(int u,int c)
{color[u]=c;for(int i=h[u];i!=-1;i=ne[i]){int j=e[i];//r如果这一点没有被染色的话,那么就对其进行染色if(!color[j]){/*不难发现,对其进行染色的过程是在dfs中‘color[u]=c;’的这一步*///染色完毕后,如果染的颜色与上一个颜色相同,则else if语句会返回false//那么就不会形成二分图,返回false;if(!dfs(j,3-c)) return false;}//如果该颜色与上一个颜色相同,则二分图不成立else if(color[j]==c) return false;}return true;
}int main()
{cin >> n >> m;memset(h,-1,sizeof h);for(int i=0;i<m;i++){int a,b;cin >> a >> b;add(a,b),add(b,a);}bool flag=true;for(int i=1;i<=n;i++){//如果没有被染色的话if(!color[i]){
//那么就对其进行染色,如果dfs返回false,那么则二分图不成立if(!dfs(i,1)){//更改标志变量flag=false;//有一个不成立,则二分图整体就不成立,break掉即可break;}}}if(flag) puts("Yes");else puts("No");return 0;
}
相关文章:

染色法判定二分图
什么是二分图? 二分图,也称作二部图,是图论中的一种特殊模型。在一个无向图G(V,E) 中,如果顶点集合 V 可以被分割成两个互不相交的子集 A 和 B,并且图中的每条边 (i,j) 关联的两个顶点 i 和 j 分别属于这两个不同的顶…...

自动气象站的主要功能优势
在科技日新月异的今天,我们生活的方方面面都受到了科技的影响。其中,自动气象站作为气象观测领域的重要一环,不仅提升了气象数据的准确性和时效性,还为我们的日常生活、农业生产、灾害预防等提供了重要的数据支持。 自动气象站概述…...

Java中实现二维数组(矩阵)的转置
在矩阵运算中,矩阵的转置是一个基本操作,即将矩阵的行变成列,列变成行。在Java中,我们可以通过编写一个方法来实现二维数组的转置。下面,我将详细介绍如何在Java中完成这一任务,并提供完整的代码示例。 编…...
Prometheus+Grafana主机运行数据
目录 介绍 安装Node Exporter 配置Prometheus 验证配置 导入仪表盘 介绍 Prometheus是一款开源的监控和警报工具,而Node Exporter是Prometheus的一个官方插件,用于采集主机上的各种系统和硬件指标。 安装Node Exporter 下载最新版本的Node Export…...

GraphQL在Postman中:释放API查询的强大潜能
🚀 GraphQL在Postman中:释放API查询的强大潜能 Postman作为API开发和测试的领先工具,对GraphQL的支持为开发者提供了一种新的方式来查询和管理数据。GraphQL是一种查询语言,用于API,允许客户端明确指定他们需要哪些数…...

大语言模型里的微调vs RAG vs 模板提示词
文章目录 介绍微调(Fine-tuning)定义优点:缺点:应用场景:技术细节 检索增强生成(RAG,Retrieval-Augmented Generation)定义优点:缺点:应用场景:技…...

网络编程:常用网络测试工具
telnet netstat ping arp wireshark(网络抓包工具) tcpdumpssh2 secure crt ——软件工具sudo ufw disable sudo apt-get install openssh-server openssh-client //两个命令敲完 得重启sudo apt-get install wireshark 1、telnet 远程登录工具&…...
mov视频怎么改成mp4?把mov改成MP4的四个方法
mov视频怎么改成mp4?选择合适的视频格式对于确保内容质量和流通性至关重要。尽管苹果公司的mov格式因其出色的视频表现备受赞誉,但在某些情况下,它并非最佳选择,因为使用mov格式可能面临一些挑战。MP4格式在各种设备(如…...

力扣1472.设计浏览器历史记录
力扣1472.设计浏览器历史记录 用双指针记录历史记录 以及栈顶高度移动时会直接把之前的记录消掉 class BrowserHistory {int pos-1;int top0;string history[5010];public:BrowserHistory(string homepage) {visit(homepage);}void visit(string url) {pos ;top pos;histor…...

准大一新生开学千万要带证件照用途大揭秘
1、提前关注好都有哪些考场,以及这些考场大致在网页的哪个位置。比如我选对外经贸大学,我就直接找到第二个点进去。 2、电脑上同时开了谷歌浏览器和IE浏览器,以及手机也登陆了。亲测下来,同一时间刷新,谷歌浏览器能显示…...

QImage显示图片像素
在Qt中,QImage 类是用来表示和处理图像的。如果你想查看或显示一个图片的像素数据,你可以使用 QImage 提供的方法来访问这些数据。以下是一些基本的方法来获取和显示图片的像素信息: 获取图像的像素格式: 使用 QImage::format() …...
uniapp使用高德地图(公众号+h5)
选择微信小程序的话后果就是你的地图出不来,出来了就报key异常 下面直接放配置和代码: 打包后的高德uni-app,uniCloud,serverless,高德地图,申请高德地图Key,配置使用高德地图,参数说明,高德开放平台用户名,百度地图,申请百度地图Key,配置使用百度地图,…...

深度学习与浅层学习:技术变革下的竞争态势
深度学习与浅层学习:技术变革下的竞争态势 在过去十年中,深度学习的崛起对整个人工智能领域产生了巨大影响,几乎在各种任务中显示出超越传统浅层学习方法的性能。这种变化不仅推动了技术的进步,还对硬件市场,尤其是显…...

LeetCode 219. 存在重复元素 II
LeetCode 219. 存在重复元素 II 给你一个整数数组 nums 和一个整数 k ,判断数组中是否存在两个 不同的索引 i 和 j ,满足 nums[i] nums[j] 且 abs(i - j) < k 。如果存在,返回 true ;否则,返回 false 。 示例 1&am…...

【目标检测】使用自己的数据集训练并预测yolov8模型
1、下载yolov8的官方代码 地址: GitHub - ultralytics/ultralytics: NEW - YOLOv8 🚀 in PyTorch > ONNX > OpenVINO > CoreML > TFLite 2、下载目标检测的训练权重 yolov8n.pt 将 yolov8n.pt 放在ultralytics文件夹下 3、数据集分布 注…...
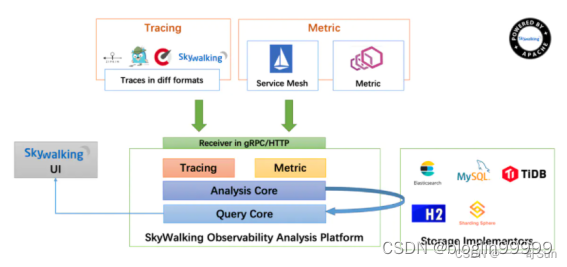
应用监控SkyWalking调研
参考: 链路追踪( Skyworking )_skywalking-CSDN博客 企业级监控项目Skywalking详细介绍,来看看呀-CSDN博客 SkyWalking 极简入门 | Apache SkyWalking 使用 SkyWalking 监控 ClickHouse Server | Apache SkyWalking https://zhuanlan.zhihu.com/p/3…...

Selenium使用注意事项:
find_element 和 find_elements 的区别 WebDriver和WebElement的区别 问题: 会遇到报错: selenium.common.exceptions.NoSuchElementException: Message: no such element: Unable to locate element: {"method":"css selector",&…...

小程序需要进行软件测试吗?小程序测试有哪些测试内容?
在如今移动互联网快速发展的时代,小程序已成为人们生活中不可或缺的一部分。然而,面对日益增长的小程序数量和用户需求,小程序的稳定性和质量问题日益突显。因此,对小程序进行软件测试显得尤为重要。 近期的一项调查显示…...

一文读懂企业租用GPU的注意事项!
在人工智能、大数据处理及高性能计算领域,GPU算力已成为推动技术创新与业务增长的核心动力。尚云Sunclouds作为GPU算力租赁服务提供商,为用户提供了灵活、高效且成本可控的解决方案。对于初次接触GPU算力租赁的用户而言,了解并掌握租用过程中…...

Linux运维:mysql主从复制原理及实验
当一台数据库服务器出现负载的情况下,需要扩展服务器服务器性能扩展方式有向上扩展,垂直扩展。向外扩展,横向扩展。通俗的讲垂直扩展是将一台服务器扩展为性能更强的服务器。横向扩展是增加几台服务器。 主从复制好比存了1000块钱在主上&…...

3维突破:DamaiHelper自动化工具的技术原理与场景实践
3维突破:DamaiHelper自动化工具的技术原理与场景实践 【免费下载链接】DamaiHelper 大麦网演唱会演出抢票脚本。 项目地址: https://gitcode.com/gh_mirrors/dama/DamaiHelper 行业痛点诊断 在数字化服务快速发展的今天,在线资源抢订领域面临着三…...

nomic-embed-text-v2-moe实战案例:跨境电商多语SKU描述语义去重系统
nomic-embed-text-v2-moe实战案例:跨境电商多语SKU描述语义去重系统 1. 引言:跨境电商的SKU描述之痛 如果你在跨境电商平台工作过,或者自己经营过海外店铺,一定遇到过这样的头疼事:商品库里有成千上万个SKUÿ…...

深入解析MANGOS数据库结构表:魔兽世界私服开发者的终极指南
1. 从零开始:为什么你需要吃透MANGOS数据库 如果你正在折腾魔兽世界私服,或者打算自己动手搭建一个,那你肯定绕不开一个东西:MANGOS的数据库。这东西就像是你服务器的“大脑”,所有游戏世界的规则、内容、逻辑…...
)
YOLOv5+GraspNet实战:如何用Python快速搭建机械臂抓取系统(附完整代码)
从“看见”到“抓取”:用YOLOv5与GraspNet构建高精度机械臂视觉抓取系统 想象一下,你面前的工作台上散落着几个不同形状的零件,一台机械臂需要从中准确地识别并抓取一个特定的螺丝。这听起来像是科幻电影里的场景,但今天ÿ…...

从EPS/Wind到Stata:高效转换面板数据的完整指南与常见报错解决方案
1. 为什么你的EPS/Wind数据一进Stata就“水土不服”? 做研究的朋友,尤其是经常和宏观经济、金融市场数据打交道的,肯定对EPS和Wind这两个数据库不陌生。它们就像两个巨大的数据宝库,里面装满了我们需要的各种指标。但不知道你有没…...

AlDente电池管理工具技术指南:从原理到实战
AlDente电池管理工具技术指南:从原理到实战 【免费下载链接】AlDente-Battery_Care_and_Monitoring macOS menubar tool to set Charge Limits and prolong battery lifespan 项目地址: https://gitcode.com/gh_mirrors/al/AlDente-Battery_Care_and_Monitoring …...

配置 Redis
介绍 Redis:缓存框架(工具) why使用Redis Redis介绍 Redis安装:(推荐安装Linux);重新打包,打包一份Windows(不是官方出的) 简单使用; Redis集群:(负载均衡); 优点: 使用各种语言都可以链接 redis在哪里起到作用 最牛带的Redis:即放内存,又放硬盘;(放内存的频繁要比硬盘的高很多…...

Python从入门到精通day51
前后端分离开发入门:DjangoVue.js 实战 前后端分离是现代 Web 开发的主流模式,核心是将页面渲染、交互逻辑(前端)与数据处理、业务逻辑(后端)解耦,通过标准化的 API 接口实现数据交互。本文以 …...

HY-MT1.5-1.8B优化升级:量化压缩至900MB,树莓派也能流畅运行
HY-MT1.5-1.8B优化升级:量化压缩至900MB,树莓派也能流畅运行 最近在折腾边缘设备上的AI应用,发现一个挺有意思的现象:很多号称“轻量级”的模型,真放到树莓派或者手机上一跑,要么内存爆了,要么…...

从Eclipse到Xilinx SDK:揭秘FPGA软件开发环境的构建与高效上手
1. 缘起:从熟悉的Eclipse到陌生的Xilinx SDK 如果你和我一样,是从软件或者嵌入式开发转过来玩FPGA的,第一次打开Xilinx SDK(现在叫Vitis,但核心还是它)的时候,大概率会愣一下。这界面࿰…...
