【笔试常见编程题06】最近公共祖先、求最大连续bit数、二进制插入、查找组成一个偶数最接近的两个素数

1. 最近公共祖先
将一棵无穷大满二叉树的结点按根结点一层一层地从左往右编号,根结点编号为1。现给定a,b为两个结点。设计一个算法,返回a、b最近的公共祖先的编号。注意其祖先也可能是结点本身。
测试样例:
2,3
返回:1
示例 1
输入
输出
思路1:
节点除2就是parent
大的先除直到两个数相等
class LCA {
public:int getLCA(int a, int b) {while (a != b) { if (a > b) a /= 2;else b /= 2;}return a;}
};
2. 求最大连续bit数
求一个int类型数字对应的二进制数字中1的最大连续数,例如3的二进制为00000011,最大连续2个1
数据范围:数据组数:1 ≤ t ≤ 5, 1 ≤ n ≤ 500000
进阶:时间复杂度:O(logn)空间复杂度:O(1)
输入描述
输入一个int类型数字
输出描述
输出转成二进制之后连续1的个数
示例 1
输入
200
输出
2
说明
200的二进制表示是11001000,最多有2个连续的1
思路1:
从右往左找连续的1
更新计数器,直到找到最长的连续的1
int main() {int a = 0, count = 0;while (cin >> a) {int temp = 0;for (int i = 0; i < 32; i++) {if (1 << i & a)temp++;if ((1 << i & a) == 0 || i == 31) { //如果a=-1,二进制全是1,需要加一个条件i == 31就进来count = max(temp, count); temp = 0;} }cout << count << endl;}return 0;
}
思路2:
求二进制数有几个1,n & n-1
求二进制数最长连续的1,n & (n << 1)
int main()
{int n;while (cin >> n) {int count = 0;while (n) {n = n & (n << 1);count++;}cout << count << endl;}return 0;
}
3. 二进制插入
给定两个32位整数n和m,同时给定i和j,将m的二进制数位插入到n的二进制的第j到第i位,保证n的第j到第i位均为零,且m的二进制位数小于等于i-j+1,其中二进制的位数从0开始由低到高。
测试样例:
1024,19,2,6
返回:1100
示例 1
输入
输出
思路1:

class BinInsert {
public:int binInsert(int n, int m, int j, int i) {m <<= j;return n + m;}
};
class BinInsert {
public:int binInsert(int n, int m, int j, int i) {while(j) {m *= 2;j--;}return n + m;}
};
4. 查找组成一个偶数最接近的两个素数
任意一个偶数(大于2)都可以由2个素数组成,组成偶数的2个素数有很多种情况,本题目要求输出组成指定偶数的两个素数差值最小的素数对。
数据范围:输入的数据满足
输入描述
输入一个大于2的偶数
输出描述
从小到大输出两个素数
示例 1
输入
20
输出
7
13
示例 2
输入
4
输出
2
2
思路1:
中间组成偶数的两个素数差值最小
从中间往两边找差值最小素数
#include <iostream>
using namespace std;// 质数又称素数。指在一个大于1的自然数中,除了1和此整数自身外,没法被其他自然数整除的数
bool isPrime(int n) { // 经常用到的功能封装成函数会更方便for (int i = 2; i <= n / 2; i++) {if (n % i == 0)return false;}return true; // 遍历完都没有就是素数
}int main() { int n;while (cin >> n) {for (int i = n/2; i > 0; i--) if (isPrime(i) && isPrime(n - i)) {cout << i << '\n' << n - i << endl;break;}}return 0;
}
相关文章:

【笔试常见编程题06】最近公共祖先、求最大连续bit数、二进制插入、查找组成一个偶数最接近的两个素数
1. 最近公共祖先 将一棵无穷大满二叉树的结点按根结点一层一层地从左往右编号,根结点编号为1。现给定a,b为两个结点。设计一个算法,返回a、b最近的公共祖先的编号。注意其祖先也可能是结点本身。 测试样例: 2,3 返回&a…...

【工具分享】Gophish——网络钓鱼框架
文章目录 Gophish安装方式功能简介 Gophish Gophish 是一个开源的网络钓鱼框架,它被设计用于模拟真实世界的钓鱼攻击,以帮助企业和渗透测试人员测试和评估他们的网络钓鱼风险。Gophish 旨在使行业级的网络钓鱼培训对每个人都是可获取的,它易…...

“职业三大底层逻辑“是啥呢?
大家好,我是有用就扩散。 掌握职业发展的三大底层逻辑以宏观视角看待自己的职业发展道路具备长远规划自己职业路劲的能力通过成就事件呈现自己的工作成绩 一、痛点陈述 不喜欢眼前的工作?眼前的工作琐碎没前途?找不到能力提升的方向时候会…...

飞睿智能无线高速uwb安全数据传输模块,低功耗、抗干扰超宽带uwb芯片传输速度技术新突破
在信息化的时代,数据传输的速度和安全性无疑是每个企业和个人都极为关注的话题。随着科技的飞速发展,超宽带(Ultra-Wideband,简称UWB)技术凭借其性能和广泛的应用前景,逐渐成为了数据传输领域的新星。今天&…...

手把手教你从微信中取出聊天表情图片,以动态表情保存为gif为例
以下方法静态图片同样适用 收到动画表情像保存为gif 这时候我们就要借助微信官方的文件小助手网页版。 登录之后把要保存的表情转发给微信传输助手 这个时候就会出现将图像另存为 如果需要保存动图就修改后缀为.gif...

【深度学习】图形模型基础(5):线性回归模型第三部分:线性回归模型拟合
1.引言 本博文专辑的焦点主要集中在回归模型的实用案例和工具上,从简单的单变量线性回归入手,逐步过渡到包含多个预测变量、非线性模型,以及在预测和因果推断中的应用。本文我们将介绍回归模型推断的一些数学结构,并提供一些代数…...

【Git 入门】初始化配置与新建仓库
文章目录 前言配置git新建仓库仓库的概念创建仓库命令总结前言 在现代软件开发中,版本控制系统已经成为了不可或缺的工具。其中,Git 是最为广泛使用的版本控制系统之一。Git 不仅可以帮助我们管理和跟踪代码的变化,还可以方便地与他人协作。本文将介绍 Git 的基础知识,包括…...

C语言 求两个整数的最大公约数和最小公倍数
写两个函数,分别求两个整数的最大公约数和最小公倍数,用主函数调用这两个函数,并输出结果。两个整数由键盘输入。 #include <stdio.h>// 求最大公约数 int gcd(int a, int b) {while (b ! 0) {int temp b;b a % b;a temp;}return a; }// 求最小公倍数 int lcm(int a,…...

Linux arm64平台指令替换函数 aarch64_insn_patch_text_nosync
文章目录 前言一、简介1.1 aarch64_insn_patch_text_nosync1.2 aarch64_insn_write1.3 patch_map1.4 set_fixmap_offset1.5 __set_fixmap 二、用途2.1 jump lable2.2 ftrace 参考资料 前言 这篇文章介绍了 Linux x86_64平台指令替换函数 text_poke_smp/bp 接下来介绍arm64平台…...

谷歌浏览器插件开发笔记0.1.033
谷歌浏览器插件开发笔记0.1.000 示例文件manifest.jsonpopup.htmloptions.jsoptions.htmlcontent.jsbackground.js 网页按钮快捷键插件api使用基础参考链接 示例文件 共计有6个常用的文件 manifest.json background字段:随着浏览器的打开而打开,随着浏…...

ETag:Springboot接口如何添加Tag
ETag简介 在Web开发中,ETag(Entity Tag)是一种HTTP头字段,用于标识特定版本的资源。ETag的主要用途是缓存控制和优化,通过比较客户端和服务器资源的ETag值,可以判断资源是否发生变化,从而避免不…...
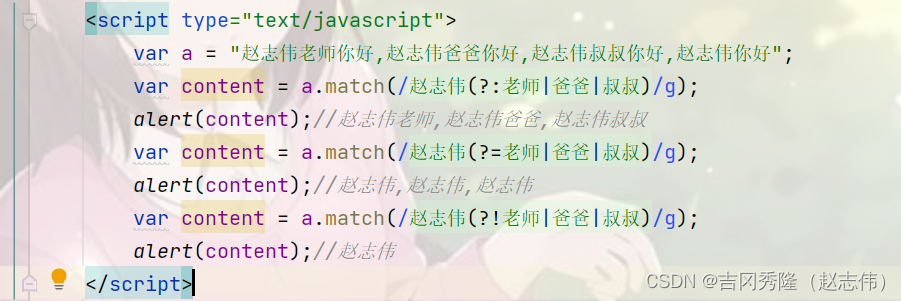
JavaSe系列二十七: Java正则表达式
正则表达式 为什么要学习正则表达式再提几个问题解决之道-正则表达式正则表达式基本介绍介绍 正则表达式底层实现实例分析 正则表达式语法基本介绍元字符-转义号 \\\\元字符-字符匹配符元字符-选择匹配符元字符-限定符元字符-定位符分组非贪婪匹配 应用实例对字符串进行如下验证…...
Depth Anything V2 复现)
(深度估计学习)Depth Anything V2 复现
Depth Anything V2 复现 一、配置环境二、准备数据1. 权重文件2. 训练数据 三、Test四、Train 代码:https://github.com/DepthAnything/Depth-Anything-V2 一、配置环境 在本机电脑win跑之后依旧爆显存,放到服务器跑:Ubuntu22.04,…...

C语言——printf、scanf、其他输入输出函数
printf函数 1.printf 函数的一般格式: printf 函数的一般格式为printf(格式控制,输出表列) 例如: printf("%d,%c\n",i,c); (1)“格式控制" 是用双撇号括起来的一个字符串,称“转换控制字符串”,简称“格式字符串”。它包括…...

adb 常用的命令总结
1、adb logcat 抓取日志 adb logcat > d:\log.txt Ctrlc 结束日志抓取 adb logcat -c > d:\log.txt 清空旧日志 发生Native Crash 时,抓取错误报告 adb logcat -b crash 抓取筛选后的日志: adb logcat -s AndroidRuntime > d:\log…...

Java发展过程中,JVM的演进
1. 初期的JVM(Java 1.0 到 Java 1.1) Java 1.0 于1996年发布,最初的JVM设计主要是为了跨平台兼容性和基本的垃圾回收功能。早期的JVM以解释执行字节码为主,性能相对较低。 2. 引入即时编译(JIT)ÿ…...

笔记:在Entity Framework Core中如何处理多线程操作DbContext
一、目的: 在使用Entity Framework Core (EF Core) 进行多线程操作时,需要特别注意,因为DbContext类并不是线程安全的。这意味着,你不能从多个线程同时使用同一个DbContext实例进行操作。尝试这样做可能会导致数据损坏、异常或不可…...

RabbitMQ 高级功能
RabbitMQ 是一个广泛使用的开源消息代理,它支持多种消息传递协议,可以在分布式系统中用于可靠的消息传递。除了基本的消息队列功能外,RabbitMQ 还提供了一些高级功能,增强了其在高可用性、扩展性和灵活性方面的能力。以下是一些主…...

软件架构之开发管理
软件架构之开发管理 第 13 章:开发管理13.1 项目的范围、时间与成本13.1.1 项目范围管理13.1.2 项目成本管理13.1.3 项目时间管理 13.2 配置管理与文档管理13.2.1 软件配置管理的概念13.2.2 软件配置管理的解决方案13.2.3 软件文档管理 13.3 软件需求管理13.3.1 需求…...

【Linux 基础】df -h 的输出信息解读
df -h 的输出信息 xxx:~$ df -h Filesystem Size Used Avail Use% Mounted on udev 16G 0 16G 0% /dev tmpfs 3.2G 792K 3.2G 1% /run /dev/sda1 32G 1.7G 30G 6% / tmpfs 16G 0 16G 0% /dev/shm tmp…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...
