[python][whl]causal-conv1d的python模块在windows上whl文件下载
【模块介绍】
causal-conv1d,即因果一维卷积(Causal 1D Convolution),是一种在深度学习特别是时序数据处理中广泛应用的卷积技术。它主要特点在于其“因果性”,即输出的每个元素仅依赖于输入序列中它之前的元素,而不考虑未来的输入。这种特性使得因果一维卷积在处理如语音处理、时间序列预测等任务时非常有用,因为它确保了模型的预测是基于到当前时刻为止的所有可用信息。
在技术实现上,causal-conv1d通常通过对标准的一维卷积(Conv1D)进行特定的填充(padding)操作来实现因果性。具体来说,它会在输入序列的起始端添加足够数量的零填充,以确保卷积核在滑动过程中不会超出输入序列的当前位置,从而保持因果性。
此外,causal-conv1d还允许通过调整扩张率(dilation)等参数来进一步控制感受野的大小,从而在不增加参数数量的前提下提高模型对输入序列的捕获能力。
causal-conv1d的实现和使用通常依赖于深度学习框架,如PyTorch、TensorFlow等,这些框架提供了丰富的API来支持各种类型的卷积操作,包括因果一维卷积。在实际应用中,开发者可以通过这些框架的文档和示例代码来学习和使用causal-conv1d。
总的来说,causal-conv1d是一种强大的时序数据处理工具,它通过保持因果性来确保模型的预测基于到当前时刻为止的所有可用信息,从而在处理如语音、时间序列等时序数据时表现出色。
【下载地址】
causal_conv1d-1.1.1-cp310-cp310-win_amd64.whl
注意上面模块只能在python3.10环境下面且操作系统为windows x64系统下使用,安装方式很简单只需要pip install causal_conv1d-1.1.1-cp310-cp310-win_amd64.whl
文件下载地址:
https://download.csdn.net/download/FL1623863129/89536605
相关文章:

[python][whl]causal-conv1d的python模块在windows上whl文件下载
【模块介绍】 causal-conv1d,即因果一维卷积(Causal 1D Convolution),是一种在深度学习特别是时序数据处理中广泛应用的卷积技术。它主要特点在于其“因果性”,即输出的每个元素仅依赖于输入序列中它之前的元素&#…...

介绍 CM3leon,一个更高效、最先进的文本和图像生成模型
近几个月来,随着让机器理解和表达语言的自然语言处理技术以及可根据文本输入生成图像的系统的进步,人们对生成式人工智能模型的兴趣和研究也在加速。今天,我们要展示的是 CM3leon(发音类似于 “变色龙”),它…...

HTTPS和HTTP有哪些区别
两者的主要区别在于安全性和数据加密: 加密层:HTTPS 在HTTP 的基础上增加了SSL/TLS 协议作为加密层,确保数据传输的安全性,即使数据被截获,没有相应的密钥也无法解读数据内容。而HTTP 数据传输是明文的,容易受到攻击。…...

Docker 安装 PostgreSQL
1. 启动 PostgreSQL 容器 docker run --name ffj-postgres -p 5432:5432 -e POSTGRES_PASSWORDCisc0123 -d postgres docker run:启动一个新的容器。--name指定容器名称为 ffj-postgres。-p 5432:5432:将主机的 5432 端口映射到容器的 5432 端口。-e P…...

实践致知第12享:如何新建一个Word并设置格式
一、背景需求 小姑电话说:要新建一个Word文档,并将每段的首行设置空2格。 二、解决方案 1、在电脑桌面上空白地方,点击鼠标右键,在下拉的功能框中选择“DOC文档”或“DOCX文档”都可以,如下图所示。 之后࿰…...

Rust vs Go: 特点与应用场景分析
目录 介绍Rust的特点Go的特点Rust的应用场景Go的应用场景总结 介绍 Rust和Go(Golang)是现代编程语言中两个非常流行的选择。凭借各自的独特优势和广泛的应用场景,吸引了大量开发者的关注。本文将详细介绍Rust和Go的特点,并探讨它…...

2024的开放式耳机排行榜,看这六个耳机选购的小Tips
寻找一款既能聊天又能听歌的耳机并不容易,但是开放式耳机可能会是一个理想的选择。与传统的入耳式耳机相比,开放式耳机可以让你更加自然地与周围环境互动,并且不容易掉落。当然,在市场上选择一款适合自己的开放式耳机也是至关重要…...

JAVA-报表模糊搜索询易实现
背景: 一般文件报表经常会需要搜各个表头对应内容,如果支持全部类型切换搜索,操作起来就不够便捷。而且这个报表是测试自己用的,准确性可以不用太要求,所以更想要那中输入关键字命中任意表记录内容的模糊匹配功能。 方法一:解析搜…...

牛客 7.13 月赛(留 C逆元)
B-最少剩几个?_牛客小白月赛98 (nowcoder.com) 思路 奇数偶数 奇数;奇数*偶数 奇数 所以在既有奇数又有偶数时,两者结合可以同时删除 先分别统计奇数,偶数个数 若偶个数大于奇个数,答案是偶个数-奇个数 若奇个数…...

FPGA之术语
FPGA之术语 IOSTANDARDDIFF_SSTL12:LVCMOS33:sys_clk_p/n:rst_n:UART时钟JTAG:GPIOONFIPCIe IOSTANDARD 在电子工程领域,DIFF_SSTL12和LVCMOS33是两种不同的电气标准,用于定义信号的电压级别和特性。 IOSTANDARD是一个在FPGA(现场可编程门阵…...

WPF透明置顶窗口wine适配穿透问题解决
一、透明窗口全屏时,鼠标不穿透 问题描述 我有一个透明窗口,它是一个全屏置顶窗口,窗口里面有一个工具条,可以通过鼠标拖动工具条的位置,程序启动后,在不点击工具条的时候,鼠标是可以穿透的&a…...
方法的使用)
浅析Kafka Streams中KTable.aggregate()方法的使用
KTable.aggregate() 方法是 Apache Kafka Streams API 中用于对流数据进行状态化聚合的核心方法之一。这个方法允许你根据一个键值(通常是<K,V>类型)的流数据,应用一个初始值和一个聚合函数,来累积和更新一个状态࿰…...

java word转pdf、word中关键字位置插入图片 工具类
java word转pdf、word中关键字位置插入图片 工具类 1.pom依赖 <dependency><groupId>org.apache.poi</groupId><artifactId>poi</artifactId><version>3.15</version></dependency><dependency><groupId>org.apa…...

jail内部ubuntu apt升级失败问题解决
在FreeBSD jail 里安装启动Ubuntu jammy系统,每次装好执行jexec ubjammy sh进入Ubuntu系统后,执行apt update报错。 这个问题困惑了好久,突然有一天仔细去看报错信息,查看了(man 5 apt.conf) ,才搞定问题。简单来说就是…...

迎接AI新时代:GPT-5的技术飞跃与未来展望
引言 随着人工智能技术的迅猛发展,大语言模型在过去几年取得了显著进步。OpenAI最新的声明表明,GPT-5将在一年半后发布,并将带来从高中生智力水平到博士生智力水平的飞跃。这一突破引起了科技界和公众的广泛关注。本文将从技术突破预测、智能…...

Snap Video:用于文本到视频合成的扩展时空变换器
图像生成模型的质量和多功能性的显著提升,研究界开始将其应用于视频生成领域。但是视频内容高度冗余,直接将图像模型技术应用于视频生成可能会降低运动的保真度和视觉质量,并影响可扩展性。来自 Snap 的研究团队及其合作者提出了 "Snap …...

实验8 视图创建与管理实验
一、实验目的 理解视图的概念。掌握创建、更改、删除视图的方法。掌握使用视图来访问数据的方法。 二、实验内容 在job数据库中,有聘任人员信息表:Work_lnfo表,其表结构如下表所示: 其中表中练习数据如下: 1.‘张明…...

C++ 开源库
1 PDFium PDFium 是一个开源的 PDF 渲染和处理库,最初由 Foxit Software 开发,并于2014年捐赠给了 Chromium 项目。PDFium 旨在为各种应用程序提供高效、灵活的 PDF 渲染和操作功能。 2 代码地址 https://github.com/chromium/pdfium 主要特性 渲染…...
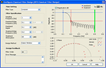
LabVIEW滤波器性能研究
为了研究滤波器的滤波性能,采用LabVIEW设计了一套滤波器性能研究系统。该系统通过LabVIEW中的波形生成函数,输出幅值及频率可调的正弦波和白噪声两种信号,并将白噪声与正弦波叠加,再通过滤波器输出纯净的正弦波信号。系统通过FFT&…...

『C++成长记』vector模拟实现
🔥博客主页:小王又困了 📚系列专栏:C 🌟人之为学,不日近则日退 ❤️感谢大家点赞👍收藏⭐评论✍️ 目录 一、存储结构 二、默认成员函数 📒2.1构造函数 📒2.2拷贝…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

2.2.2 ASPICE的需求分析
ASPICE的需求分析是汽车软件开发过程中至关重要的一环,它涉及到对需求进行详细分析、验证和确认,以确保软件产品能够满足客户和用户的需求。在ASPICE中,需求分析的关键步骤包括: 需求细化:将从需求收集阶段获得的高层需…...

mcts蒙特卡洛模拟树思想
您这个观察非常敏锐,而且在很大程度上是正确的!您已经洞察到了MCTS算法在不同阶段的两种不同行为模式。我们来把这个关系理得更清楚一些,您的理解其实离真相只有一步之遥。 您说的“select是在二次选择的时候起作用”,这个观察非…...
