【PyTorch单点知识】自动求导机制的原理与实践
文章目录
- 0. 前言
- 1. 自动求导的基本原理
- 2. PyTorch中的自动求导
- 2.1 创建计算图
- 2.2 反向传播
- 2.3 反向传播详解
- 2.4 梯度清零
- 2.5 定制自动求导
- 3. 代码实例:线性回归的自动求导
- 4. 结论
0. 前言
按照国际惯例,首先声明:本文只是我自己学习的理解,虽然参考了他人的宝贵见解及成果,但是内容可能存在不准确的地方。如果发现文中错误,希望批评指正,共同进步。
在深度学习中,自动求导(Automatic Differentiation, AD)是一项至关重要的技术,它使我们能够高效地计算神经网络的梯度,进而通过反向传播算法更新权重。
PyTorch作为一款动态计算图的深度学习框架,以其灵活性和易用性著称,其自动求导机制是其实现高效、灵活训练的核心。本文将深入探讨PyTorch中的自动求导机制,从原理到实践,通过代码示例来展示其工作流程。
如果对计算图不太了解,可以参考我的往期文章:基于TorchViz详解计算图(附代码)
1. 自动求导的基本原理
自动求导是一种数学方法,用于计算函数的导数。与数值微分相比,自动求导能够提供精确的导数计算结果,同时避免了符号微分中可能出现的手动求导错误。在深度学习中,我们通常关注的是反向模式backward的自动求导,即从输出向输入方向传播梯度的过程。
反向模式自动求导基于链式法则,它允许我们将复杂的复合函数的导数分解成多个简单函数的导数的乘积。在神经网络中,每一层都可以看作是一个简单的函数,通过链式法则,我们可以从前向传播的输出开始,逆向计算每个参数的梯度。
2. PyTorch中的自动求导
PyTorch通过其autograd模块实现了自动求导机制。autograd记录了所有的计算步骤,创建了一个计算图(Computational Graph),并在需要时执行反向传播,计算梯度。
2.1 创建计算图
在PyTorch中,当一个张量(Tensor)的requires_grad=True时,任何对该张量的操作都会被记录在计算图中。例如:
import torchx = torch.ones(2, 2, requires_grad=True)
y = x + 2
z = y * y * 3
out = z.mean()print(y.grad_fn) # 查看y的计算节点
print(z.grad_fn) # 查看z的计算节点
输出为:
<AddBackward0 object at 0x000001CADEC6AB60>
<MulBackward0 object at 0x000001CADEC6AB60>
在上述代码中,z的计算节点显示了z是如何由y计算得来的,而y的计算节点则显示了y是如何由x计算得来的。这样就形成了一个计算图。
2.2 反向传播
一旦我们完成了前向传播并得到了最终的输出,就可以调用out.backward()来进行反向传播,计算梯度。例如:
import torchx = torch.ones(2, 2, requires_grad=True)
y = x + 2
z = y * y * 3
out = z.mean()out.backward()
print(x.grad)
这里,x.grad就是out相对于x的梯度。输出为:
tensor([[4.5000, 4.5000],[4.5000, 4.5000]])
2.3 反向传播详解
下面我们来详细分析下1.2节的具体计算过程:
- 首先,创建了一个2x2的张量
x,其值全为1,并且设置了requires_grad=True,这意味着PyTorch将会追踪这个张量上的所有操作,以便能够计算梯度。
x = torch.ones(2, 2, requires_grad=True)
- 然后,将
x与2相加得到y:
y = x + 2
此时y的值为:
tensor([[3., 3.],[3., 3.]])
- 接下来,将
y的每个元素平方再乘以3得到z:
z = y * y * 3
此时z的值为:
tensor([[27., 27.],[27., 27.]])
- 计算
z的平均值作为输出out:
out = z.mean()
此时out的值为:
tensor(27.)
- 使用
backward()函数对out进行反向传播,计算梯度:
out.backward()
- 最后,打印
x的梯度:
print(x.grad)
由于out是通过一系列操作从x得到的,我们可以根据链式法则计算出x的梯度。具体来说,out相对于x的梯度可以通过以下步骤计算得出:
out相对于z的梯度是1/z.size(0)(因为z.mean()是对z的所有元素取平均),这里z.size(0)等于4,所以out相对于z的梯度是1/4。z相对于y的梯度是y * 3 * 2(因为z = y^2 * 3,所以dz/dy = 2*y*3)。y相对于x的梯度是1(因为y = x + 2,所以dy/dx = 1)。
综合以上,out相对于x的梯度是:
1/4 * (y * 3 * 2) * 1
由于y的值为[[3, 3], [3, 3]],那么上述梯度计算结果为:
1/4 * (3 * 3 * 2) * 1 = 9/2 = 4.5
因此,最终x.grad的值为:
tensor([[4.5000, 4.5000],[4.5000, 4.5000]])
2.4 梯度清零
在多次迭代中,梯度会累积在张量中,因此在每次迭代开始之前,我们需要调用optimizer.zero_grad()来清零梯度,防止梯度累积。(PyTorch为了训练方便,会默认梯度累积)
2.5 定制自动求导
PyTorch还允许我们定义自己的自动求导函数,通过继承torch.autograd.Function类并重写forward和backward方法。这为实现更复杂的计算提供了可能。
3. 代码实例:线性回归的自动求导
接下来,我们将通过一个简单的线性回归问题,演示PyTorch自动求导机制的实际应用。
假设我们有一组数据点,我们想找到一条直线(y = wx + b),使得这条直线尽可能接近这些数据点。我们的目标是最小化损失函数(例如均方误差)。
import torch
import numpy as np# 准备数据
np.random.seed(0)
X = np.random.rand(100, 1)
Y = 2 + 3 * X + 0.1 * np.random.randn(100, 1)X = torch.from_numpy(X).float()
Y = torch.from_numpy(Y).float()# 初始化权重和偏置
w = torch.tensor([1.], requires_grad=True)
b = torch.tensor([1.], requires_grad=True)# 定义模型和损失函数
def forward(x):return w * x + bloss_fn = torch.nn.MSELoss()# 训练循环
learning_rate = 0.01
for epoch in range(1000):# 前向传播y_pred = forward(X)# 计算损失loss = loss_fn(y_pred, Y)# 反向传播loss.backward()# 更新权重with torch.no_grad():w -= learning_rate * w.gradb -= learning_rate * b.grad# 清零梯度w.grad.zero_()b.grad.zero_()if (epoch+1) % 100 == 0:print(f'Epoch [{epoch+1}/1000], Loss: {loss.item():.4f}')print('Final weights:', w.item(), 'bias:', b.item())
输出:
Epoch [100/1000], Loss: 0.1273
Epoch [200/1000], Loss: 0.0782
Epoch [300/1000], Loss: 0.0620
Epoch [400/1000], Loss: 0.0497
Epoch [500/1000], Loss: 0.0404
Epoch [600/1000], Loss: 0.0332
Epoch [700/1000], Loss: 0.0277
Epoch [800/1000], Loss: 0.0235
Epoch [900/1000], Loss: 0.0203
Epoch [1000/1000], Loss: 0.0179
Final weights: 2.68684983253479 bias: 2.17771577835083
在这个例子中,我们首先准备了一些随机生成的数据,然后初始化了权重w和偏置b。在训练循环中,我们通过前向传播计算预测值,使用均方误差损失函数计算损失,然后通过调用loss.backward()进行反向传播,最后更新权重和偏置。通过多次迭代,我们最终找到了使损失最小化的权重和偏置。
4. 结论
PyTorch的自动求导机制是其强大功能的关键所在。通过autograd模块,PyTorch能够自动跟踪计算图并高效地计算梯度,这大大简化了深度学习模型的开发过程。本文通过理论解释和代码示例,深入探讨了PyTorch中的自动求导机制,希望读者能够从中获得对这一重要概念的深刻理解,并在实际项目中灵活运用。
相关文章:

【PyTorch单点知识】自动求导机制的原理与实践
文章目录 0. 前言1. 自动求导的基本原理2. PyTorch中的自动求导2.1 创建计算图2.2 反向传播2.3 反向传播详解2.4 梯度清零2.5 定制自动求导 3. 代码实例:线性回归的自动求导4. 结论 0. 前言 按照国际惯例,首先声明:本文只是我自己学习的理解&…...

【Java】搜索引擎设计:信息搜索怎么避免大海捞针?
一、内容分析 我们准备开发一个针对全网内容的搜索引擎,产品名称为“Bingoo”。 Bingoo的主要技术挑战包括: 针对爬虫获取的海量数据,如何高效地进行数据管理;当用户输入搜索词的时候,如何快速查找包含搜索词的网页…...

【Python】ModuleNotFoundError: No module named ‘distutils.util‘ bug fix
【Python】ModuleNotFoundError: No module named distutils.util bug fix 1. error like this2. how to fix why this error occured , because i remove the origin version python of ubuntu of 20.04. then the system trapped in tty1 , you must make sure the laptop li…...

痉挛性斜颈对生活有哪些影响?
痉挛性斜颈,这个名字听起来可能并不熟悉,但它实际上是一种神经系统疾病,影响着全球数百万人的生活质量。它以一种无法控制的方式,使患者的颈部肌肉发生不自主的收缩,导致头部姿势异常。对于患者来说,痉挛性…...

Javassist 修改 jar 包里的 class 文件
前言 Javassist 是一个用于处理 Java 字节码的类库,可以用以修改 class 文件或 jar 包里的 class 文件。 简单来说我们用Java编写的代码是放在 java 格式的代码文件里,在编译的时候会编译为 class 格式的字节码文件,然后一般所有 class 文件…...

交换机的二三层原理
相同VLAN的交换机交换原理(二层交换原理): 交换机收到数据帧,首先会检查数据帧的VLAN标签和目标MAC,若属于相同VLAN,且该目标MAC在本地MAC表中,则直接根据出接口进行数据转发 不同VLAN的交换机…...

HarmonyOS ArkUi 字符串<展开/收起>功能
效果图: 官方API: ohos.measure (文本计算) 方式一 measure.measureTextSize 跟方式二使用一样,只是API调用不同,可仔细查看官网方式二 API 12 import { display, promptAction } from kit.ArkUI import { MeasureUtils } fr…...

Lianwei 安全周报|2024.07.09
新的一周又开始了,以下是本周「Lianwei周报」,我们总结推荐了本周的政策/标准/指南最新动态、热点资讯和安全事件,保证大家不错过本周的每一个重点! 政策/标准/指南最新动态 01 《数字中国发展报告(2023年)…...

火遍全网的15个Python的实战项目,你该不会还不知道怎么用吧!
经常听到有朋友说,学习编程是一件非常枯燥无味的事情。其实,大家有没有认真想过,可能是我们的学习方法不对? 比方说,你有没有想过,可以通过打游戏来学编程? 今天我想跟大家分享几个Python小游…...

快速使用BRTR公式出具的大模型Prompt提示语
Role:文章模仿大师 Background: 你是一位文章模仿大师,擅长分析文章风格并进行模仿创作。老板常让你学习他人文章后进行模仿创作。 Attention: 请专注在文章模仿任务上,提供高质量的输出。 Profile: Author: 一博Version: 1.0Language: 中文Descri…...

Xilinx FPGA DDR4 接口的 PCB 准则
目录 1. 简介 1.1 FPGA-MIG 与 DDR4 介绍 1.2 DDR4 信号介绍 1.2.1 Clock Signals 1.2.2 Address and Command Signals 1.2.3 Control Signals 1.2.4 Data Signals 1.2.5 Other Signals 2. 通用存储器布线准则 3. Xilinx FPGA-MIG 的 PCB 准则 3.1 引脚配置 3.1.1 …...

神经网络 | Transformer 基本原理
目录 1 为什么使用 Transformer?2 Attention 注意力机制2.1 什么是 Q、K、V 矩阵?2.2 Attention Value 计算流程2.3 Self-Attention 自注意力机制2.3 Multi-Head Attention 多头注意力机制 3 Transformer 模型架构3.1 Positional Encoding 位置编…...

浅析 VO、DTO、DO、PO 的概念
文章目录 I 浅析 VO、DTO、DO、PO1.1 概念1.2 模型1.3 VO与DTO的区别I 浅析 VO、DTO、DO、PO 1.1 概念 VO(View Object) 视图对象,用于展示层,它的作用是把某个指定页面(或组件)的所有数据封装起来。DTO(Data Transfer Object): 数据传输对象,这个概念来源于J2EE的设…...
7.8 CompletableFuture
Future 接口理论知识复习 Future 接口(FutureTask 实现类)定义了操作异步任务执行的一些方法,如获取异步任务的执行结果、取消任务的执行、判断任务是否被取消、判断任务执行是否完毕等。 比如主线程让一个子线程去执行任务,子线…...
iPad锁屏密码忘记怎么办?有什么方法可以解锁?
当我们在日常使用iPad时,偶尔可能会遇到忘记锁屏密码的尴尬情况。这时,不必过于担心,因为有多种方法可以帮助您解锁iPad。接下来,小编将为您详细介绍这些解决方案。 一、使用iCloud的“查找我的iPhone”功能 如果你曾经启用了“查…...
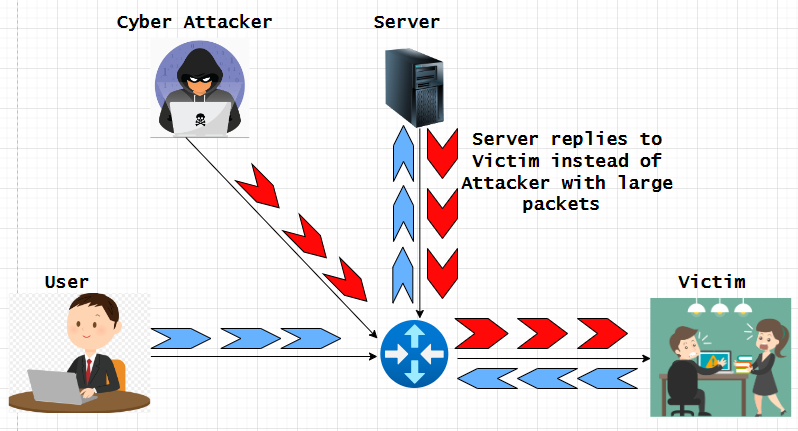
了解并缓解 IP 欺骗攻击
欺骗是黑客用来未经授权访问计算机或网络的一种网络攻击,IP 欺骗是其他欺骗方法中最常见的欺骗类型。通过 IP 欺骗,攻击者可以隐藏 IP 数据包的真实来源,使攻击来源难以知晓。一旦访问网络或设备/主机,网络犯罪分子通常会挖掘其中…...

java LogUtil输出日志打日志的class文件内具体方法和行号
最近琢磨怎么把日志打的更清晰,方便查找问题,又不需要在每个class内都创建Logger对象,还带上不同的颜色做区分,简直不要太爽。利用堆栈的方向顺序拿到日志的class问题。看效果,直接上代码。 1、demo test 2、输出效果…...

02. Hibernate 初体验之持久化对象
1. 前言 本节课程让我们一起体验 Hibernate 的魅力!编写第一个基于 Hibernate 的实例程序。 在本节课程中,你将学到 : Hibernate 的版本发展史;持久化对象的特点。 为了更好地讲解这个内容,这个初体验案例分上下 2…...
MySQL超详细学习教程,2023年硬核学习路线
文章目录 前言1. 数据库的相关概念1.1 数据1.2 数据库1.3 数据库管理系统1.4 数据库系统1.5 SQL 2. MySQL数据库2.1 MySQL安装2.2 MySQL配置2.2.1 添加环境变量2.2.2 新建配置文件2.2.3 初始化MySQL2.2.4 注册MySQL服务2.2.5 启动MySQL服务 2.3 MySQL登录和退出2.4 MySQL卸载2.…...

初识SpringBoot
1.Maven Maven是⼀个项⽬管理⼯具, 通过pom.xml⽂件的配置获取jar包,⽽不⽤⼿动去添加jar包 主要功能 项⽬构建管理依赖 构建Maven项目 1.1项目构建 Maven 提供了标准的,跨平台(Linux, Windows, MacOS等)的⾃动化项⽬构建⽅式 当我们开发了⼀个项⽬之后, 代…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...
