html5——列表、表格
目录
列表
无序列表
有序列表
自定义列表
表格
基本结构
示例
表格的跨列
表格的跨行
列表
无序列表
<ul>【声明无序列表】
<li>河间驴肉火烧</li>【声明列表项】
<li>唐山棋子烧饼</li>
<li>邯郸豆沫</li>
<li>石家庄金毛狮子鱼</li>
</ul>

无序列表的特性:
- 没有顺序,每个<li>标签独占一行(块元素)
- 默认<li>标签项前面有个实心小圆点
- 一般用于无序类型的列表,如导航、侧边栏新闻、有规律 的图文组合模块等
有序列表
<ol>【声明有序列表】
<li>驴肉火烧</li>【声明列表项】
<li>京东煨肘子</li>
<li>牛肉罩饼</li>
<li>缸炉烧饼</li>
</ol>

有序列表的特性:
- 有顺序,每个<li>标签独占一行(块元素)
- 默认<li>标签项前面有顺序标记
- 一般用于排序类型的列表,如试卷、问卷选项等
自定义列表
<dl>【声明定义列表】
<dt>水果</dt>【声明列表项】
<dd>苹果</dd>【定义列表项内容】
<dd>桃子</dd>
<dd>李子</dd>
</dl>

定义列表的特性:
- 没有顺序,每个<dt>标签、<dd>标签独占一行(块元素)
- 默认没有标记
- 一般用于一个标题下有一个或多个列表项的情况
表格
基本结构
- 单元格
- 行
- 列
示例
<table>【表格标签】
<tr>【行标签】
<th>1行1列的标题</th>【单元格标题标签】
<th>1行2列的标题</th>
</tr>
<tr>
<td>1行1列的单元格</td>【单元格标签】
<td>1行2列的单元格</td>
</tr>
</table>

表格的跨列
<table>
<tr>
<td colspan="2">学生成绩</td>【所跨的列数】
</tr>
<tr>
<td>语文</td>
<td>98</td>
</tr>
<tr>
<td>数学</td>
<td>95</td>
</tr>
</table>

表格的跨行
<table >
<tr>
<td rowspan="n"> </td>
<td> </td>
</tr>
<tr>
<td> </td>
</tr>
</table>

相关文章:

html5——列表、表格
目录 列表 无序列表 有序列表 自定义列表 表格 基本结构 示例 表格的跨列 表格的跨行 列表 无序列表 <ul>【声明无序列表】 <li>河间驴肉火烧</li>【声明列表项】 <li>唐山棋子烧饼</li> <li>邯郸豆沫</li> <l…...
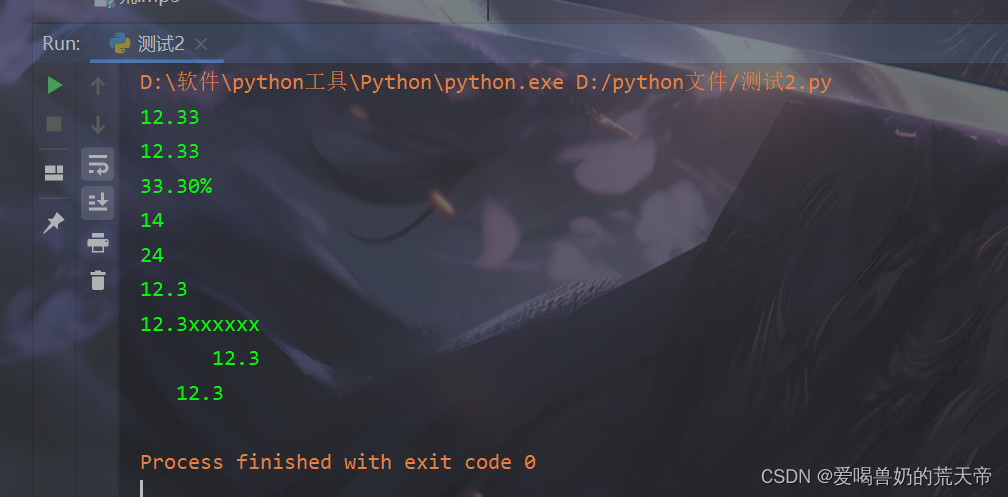
【Python字符串攻略】:玩转文字,编织程序的叙事艺术
文章目录 🚀一.字符串基础🌈二.查看数据类型⭐三.转化❤️四.字符串索引🚲五.字符串切片🎬六.字符串切片-步长☔七.反向切片注意事项🚲八.字符串💥查💥改💥删 ❤️九.字符串拼接&…...

element form表单中密码框被自动赋值,并默认背景色为白色,手动输值后背景色才是自己配置的背景色,与表单的自动填充有关
事件背景: 一个表单,有两组需要输入密码的地方,两组都被填充用户名密码,其中一组是其他信息,不是用户名密码,也被填充了,且input背景色是白色,表单中的input已经手动配置为无背景色&…...
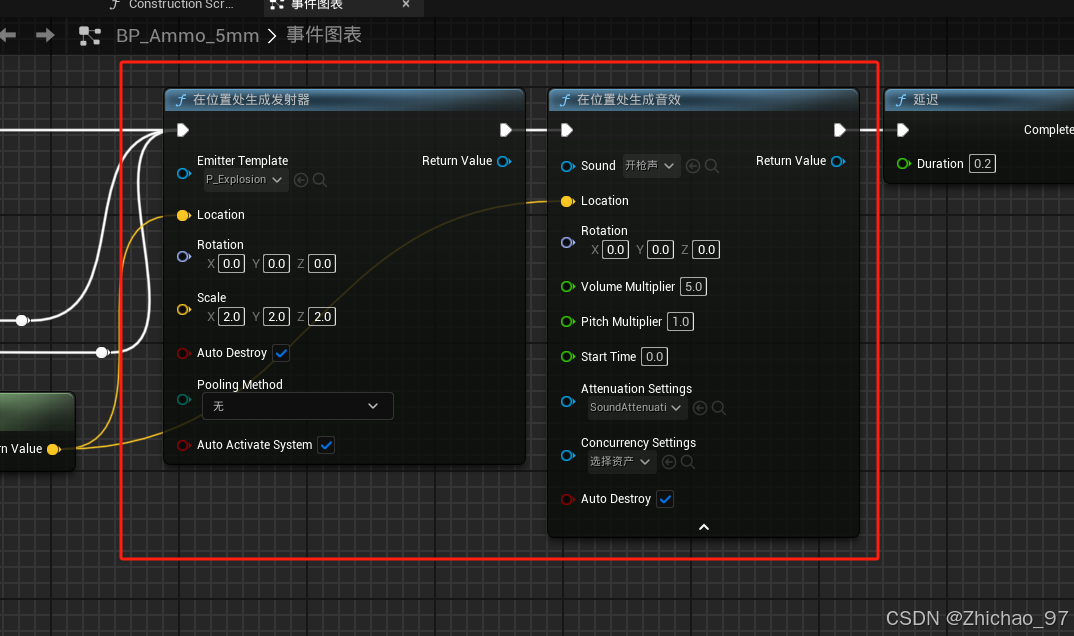
【UE5.1 角色练习】15-枪械射击——子弹发射物
目录 效果 步骤 一、创建并发射子弹 二、优化子弹 效果 步骤 一、创建并发射子弹 1. 在前面的文章中(【UE5.1 角色练习】06-角色发射火球-part1)我们创建了蓝图“BP_Skill_FireBall” 这里我们复制一份命名为“BP_Ammo_5mm”,用于表示…...

Zynq7000系列FPGA中的DMA控制器的编程限制
有关DMAC编程时适用的限制信息,有四个考虑因素: 固定非对齐突发Endian swap size restrictions:在数据传输或处理过程中,不同字节序(Endian)之间的转换和对应的限制在DMA周期内更新通道控制寄存器当MFIFO满…...

超简易高效的 AI绘图工具—与sd-webui一致界面,6G显存最高提升75%出图速率!(附安装包)
大家好,我是灵魂画师向阳 今天给大家分享一个基于Stable Diffusion WebUI 构建的AI绘图工具—sd-webui-forge,该工具的目标在于简化插件开发,优化资源管理,加速推理。 Forge承诺永远不会对Stable Diffusion WebUI用户界面添加不…...

ArduPilot开源代码之OpticalFlow_backend
ArduPilot开源代码之OpticalFlow_backend 1. 源由2. Library设计3. 重要例程3.1 OpticalFlow_backend::_update_frontend3.2 OpticalFlow_backend::_applyYaw 4. 总结5. 参考资料 1. 源由 光流计是一种低成本定位传感器,所有的光流计设备传感驱动代码抽象公共部分统…...

设计模式探索:适配器模式
1. 适配器模式介绍 1.1 适配器模式介绍 适配器模式(adapter pattern)的原始定义是:将一个类的接口转换为客户期望的另一个接口,适配器可以让不兼容的两个类一起协同工作。 适配器模式的主要作用是把原本不兼容的接口,…...

OpenCV 寻找棋盘格角点及绘制
目录 一、概念 二、代码 2.1实现步骤 2.2完整代码 三、实现效果 一、概念 寻找棋盘格角点(Checkerboard Corners)是计算机视觉中相机标定(Camera Calibration)过程的重要步骤。 OpenCV 提供了函数 cv2.findChessboardCorners…...

【深度学习】PyTorch深度学习笔记02-线性模型
1. 监督学习 2. 数据集的划分 3. 平均平方误差MSE 4. 线性模型Linear Model - y x * w 用穷举法确定线性模型的参数 import numpy as np import matplotlib.pyplot as pltx_data [1.0, 2.0, 3.0] y_data [2.0, 4.0, 6.0]def forward(x):return x * wdef loss(x, y):y_pred…...

10.FreeRTOS_互斥量
互斥量概述 在博文“ FreeRTOS_信号量 ”中,使用了二进制信号量实现了互斥,保护了串口资源。博文链接如下: FreeRTOS_信号量-CSDN博客 但还是要引入互斥量的概念。互斥量与二进制信号量相比,能够多实现如下两个功能:…...

EtherCAT总线冗余让制造更安全更可靠更智能
冗余定义 什么是总线冗余功能?我们都知道,EtherCAT现场总线具有灵活的拓扑结构,设备间支持线型、星型、树型的连接方式,其中线型结构简单、传输效率高,大多数的现场应用中也是使用这种连接方式,如下图所示…...

Android IdleHandler源码分析
文章目录 Android IdleHandler源码分析概述前提基本用法源码分析添加和删除任务执行任务 应用场景 Android IdleHandler源码分析 概述 IdleHandler是一个接口,它定义在MessageQueue类中,用于在主线程的消息队列空闲时执行一些轻量级的任务。IdleHandle…...

Mac安装stable diffusion 工具
文章目录 1.安装 Homebrew2.安装 stable diffusion webui 的依赖3.下载 stable diffusion webui 代码4.启动 stable diffusion webui 本体5.下载模型6.这里可能会遇到一个clip-vit-large-patch14报错 参考:https://brew.idayer.com/install/stable-diffusion-webui/…...

CVE-2024-6387Open SSH漏洞彻底解决举措(含踩坑内容)
一、漏洞名称 OpenSSH 远程代码执行漏洞(CVE-2024-6387) 二、漏洞概述 Open SSH是基于SSH协议的安全网络通信工具,广泛应用于远程服务器管理、加密文件传输、端口转发、远程控制等多个领域。近日被爆出存在一个远程代码执行漏洞,由于Open SSH服务器端…...

python的简单爬取
需要的第三方模块 requests winr打开命令行输入cmd 简单爬取的基本格式(爬取百度logo为例) import requests url"http://www.baidu.com/img/PCtm_d9c8750bed0b3c7d089fa7d55720d6cf.png" resprequests.get(url)#回应 #保存到本地 with open(&…...

【WEB前端2024】3D智体编程:乔布斯3D纪念馆-第60集-agent训练资讯APP重点推荐AI资讯内容(含视频)
【WEB前端2024】3D智体编程:乔布斯3D纪念馆-第60集-agent训练资讯APP重点推荐AI资讯内容(含视频) 使用dtns.network德塔世界(开源的智体世界引擎),策划和设计《乔布斯超大型的开源3D纪念馆》的系列教程。d…...

【学术会议征稿】第三届智能电网与能源系统国际学术会议
第三届智能电网与能源系统国际学术会议 2024 3rd International Conference on Smart Grid and Energy Systems 第三届智能电网与能源系统国际学术会议(SGES 2024)将于2024年10月25日-27日在郑州召开。 智能电网可以优化能源布局,让现有能源…...

01. 课程简介
1. 课程简介 本课程的核心内容可以分为三个部分,分别是需要理解记忆的计算机底层基础,后端通用组件以及需要不断编码练习的数据结构和算法。 计算机底层基础可以包含计算机网络、操作系统、编译原理、计算机组成原理,后两者在面试中出现的频…...
)
iOS热门面试题(三)
面试题1:在iOS开发中,什么是MVC设计模式?请详细解释其各个组成部分,并给出一个实际应用场景,包括具体的代码实现。 答案: MVC设计模式是一种在软件开发中广泛使用的架构模式,特别是在iOS开发中…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...
