树的前中后序的Morris遍历
目录
一.Morris遍历
1.什么是Morris遍历
2.基本思想
3.Morris遍历的优点和缺点
4.知识回顾----二叉树的线索化
二.中序Morris遍历
1.中序Morris遍历的分析
2.中序Morris遍历的思路
3.具体的代码实现
三.前序Morris遍历
1.前序Morris遍历的思路
2.具体的代码实现
四.后序Morris遍历
1.后序Morris遍历的思路
2.具体的代码实现
一.Morris遍历
1.什么是Morris遍历
Morris遍历是一种用于二叉树遍历的算法,它可以在不使用栈或队列的情况下实现中序遍历。该算法的时间复杂度为O(n),空间复杂度为O(1)。
2.基本思想
Morris遍历的基本思想是,利用叶子节点的空指针来存储临时信息,以达到节省空间的目的。具体来说,对于当前遍历到的节点,如果它有左子节点,就找到左子树中最右边的节点,将其右子节点指向当前节点,然后将当前节点更新为其左子节点。如果它没有左子节点,就输出当前节点的值,并将当前节点更新为其右子节点。重复以上步骤,直到遍历完整棵树。
3.Morris遍历的优点和缺点
Morris遍历的优点是空间复杂度低O(1),但它的缺点是会改变原来的二叉树结构,因此需要在遍历完后还原二叉树。此外,该算法可能会比递归或使用栈的算法稍微慢一些。
4.知识回顾----二叉树的线索化
二叉树的线索化,主要是利用了叶子结点中的空指针域,存放了在某种遍历顺序下的前驱或者后续结点,从而达到了线索二叉树的目的
例如,下图中序遍历结果展示如下,根据中序遍历对空指针域进行线索化
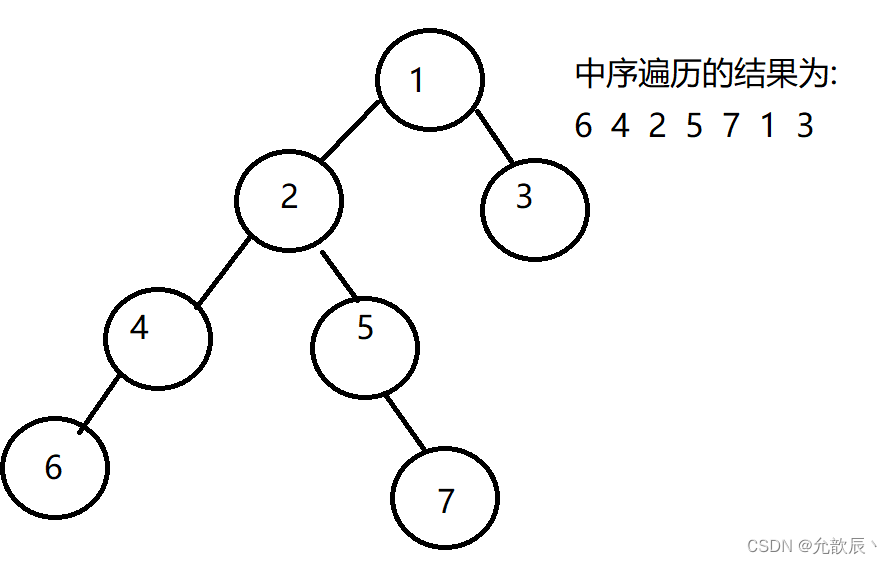
线索化的二叉树为下, 画在左边表示left结点指向,画在右边表示right指向,例如7的前驱结点为5,那么7的left指向5,7的后继节点为1,那么7的right指向1

由此,我们可能总结出这样的结论:中序遍历二叉树的指向当前结点的结点为当前结点的左子树的最右端结点,例如指向1的结点为1的左节点2的最右端结点为7,指向2结点的为2的左节点4的最右端结点4.这一点在之后的morris遍历中很重要
具体的代码实现如下:
public class InorderThreadedBinaryTree {private ThreadTreeNode pre = null;public void threadedNodes(ThreadTreeNode node) {//如果node==null,不能线索化if (node == null) {return;}//1、先线索化左子树threadedNodes(node.left);//2、线索化当前结点//处理当前结点的前驱结点//以8为例来理解//8结点的.left = null,8结点的.leftType = 1if (node.left == null) {//让当前结点的左指针指向前驱结点node.left = pre;//修改当前结点的左指针的类型,指向前驱结点node.leftType = 1;}//处理后继结点if (pre != null && pre.right == null) {//让当前结点的右指针指向当前结点pre.right = node;//修改当前结点的右指针的类型=pre.rightType = 1;}//每处理一个结点后,让当前结点是下一个结点的前驱结点pre = node;//3、线索化右子树threadedNodes(node.right);}}class ThreadTreeNode {int val;ThreadTreeNode left;//0为非线索化,1为线索化int leftType;ThreadTreeNode right;//0为非线索化,1为线索化int rightType;public ThreadTreeNode(int val) {this.val = val;}
}但是在实现Morris遍历的时候,并不需要把结点的左节点线索化,只需要把结点的右节点进行线索化即可,具体的原因在下面进行分析.
二.中序Morris遍历
1.中序Morris遍历的分析
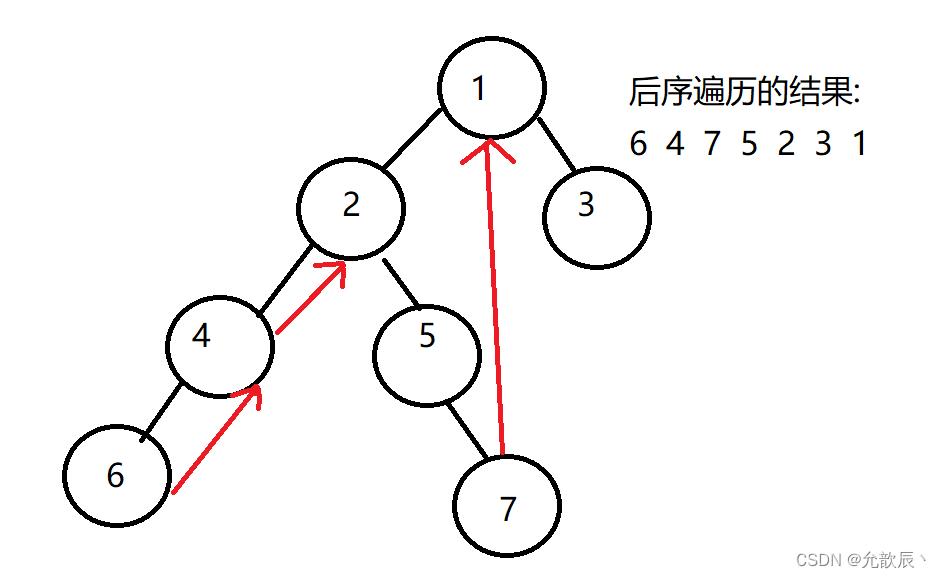
上面我们说了Morris遍历的时候只需要线索化右节点,这里给大家进行解释.当我们在中序遍历一棵树的时候,还比如是这样一棵树,我们一步步的node.left来到了6这个结点,这个结点的left为空,所以我们打印6这个结点的值,此时我们需要返回上一个结点,如果我们是要中序递归进行遍历的话,需要返回上一个栈,而我们Morris遍历的时候无法进行递归的返回,所以这个时候我们只需要把6的right结点进行线索化,这个时候6的right指向4,我们就可以返回到4,把4这个结点进行打印,4也线索化返回了2,把2进行打印,然后进行2的right结点5,5的left结点为空,因此打印5,之后进入到5的right结点7,打印7,7的right结点也进行了线索化,进入7的right结点为1,然后打印1,进入3结点并且打印
因为最好不要改变树的结构,所以我们在打印的时候,将线索化的结点的right结点置为空.

2.中序Morris遍历的思路
Morris遍历是利用了线索二叉树的思想,在遍历的过程中不适用栈,从而达到了空间复杂度为O(1)
具体的实现如下:
1.初始化当前的结点为根结点
2.若当前的结点的左节点为空,则输出当前结点,然后遍历当前结点的右子树,即'curr=curr.right'
3.若当前结点的左节点不为空,则找到当前结点的前驱节点,即当前结点左节点的最右侧结点,记为'prev'
- 如果'prev.right''为空,则将pre.right指向curr结点,然后遍历当前结点的左子树,即'curr=curr.left'
- 如果'prev.right''不为空,说明已经遍历完了当前节点的左子树,断开 `prev.right` 的连接,即'prev.left=null',输出当前节点,然后遍历当前节点的右子树,即 `curr=curr.right`.
3.具体的代码实现
public class Morris {/*** 将当前根结点中序遍历的结果存储到list集合中* @param root 根结点* @return 中序遍历的结合*/public List<Integer> inorderTraversal(TreeNode root) {List<Integer> res = new ArrayList<>();TreeNode curr = root;while (curr != null) {if (curr.left == null) { // 左子树为空,则输出当前节点,然后遍历右子树res.add(curr.val); //如果要求直接打印,直接输出System.out.println(curr.val);curr = curr.right;} else {// 找到当前节点的前驱节点TreeNode prev = curr.left;while (prev.right != null && prev.right != curr) {prev = prev.right;}if (prev.right == null) {// 将前驱节点的右子树连接到当前节点prev.right = curr;curr = curr.left;} else {// 前驱节点的右子树已经连接到当前节点,断开连接,输出当前节点,然后遍历右子树prev.right = null;res.add(curr.val);//如果要求直接打印,直接输出System.out.println(curr.val);curr = curr.right;}}}return res;}
}class TreeNode {int val;TreeNode left;TreeNode right;TreeNode(int x) {val = x;}
}测试:

还是这样一颗二叉树,输出如下:
[6, 4, 2, 5, 7, 1, 3]
三.前序Morris遍历
1.前序Morris遍历的思路
前序和中序的遍历很想,只不过在打印(收集结点信息的时候不同),中序遍历是在当前结点的左节点为空(curr.left==null),或者当前结点已经被线索化(prev.right==curr)的时候进行打印,仔细观察前序遍历的过程,我们通过修改打印的顺序即可.前序遍历是在当前结点的左节点为空(curr.left==null),或者当前结点没有被线索化(prev.right==null)的时候进行打印
具体的思路如下:
1.初始化当前的结点为根结点
2.若当前的结点的左节点为空,则输出当前结点,然后遍历当前结点的右子树,即'curr=curr.right'
3.若当前结点的左节点不为空,则找到当前结点的前驱节点,即当前结点左节点的最右侧结点,记为'prev'
- 如果'prev.right''为空,输出当前节点,然后将pre.right指向curr结点,然后遍历当前结点的左子树,即'curr=curr.left'
- 如果'prev.right''不为空,说明已经遍历完了当前节点的左子树,断开 `prev.right` 的连接,即'prev.left=null',然后遍历当前节点的右子树,即 `curr=curr.right`.

2.具体的代码实现
public List<Integer> preorderTraversal(TreeNode root) {List<Integer> res = new ArrayList<>();TreeNode curr = root;while (curr != null) {if (curr.left == null) { // 左子树为空,则输出当前节点,然后遍历右子树res.add(curr.val);//如果要求直接打印,直接输出System.out.println(curr.val);curr = curr.right;} else {// 找到当前节点的前驱节点TreeNode prev = curr.left;while (prev.right != null && prev.right != curr) {prev = prev.right;}if (prev.right == null) {res.add(curr.val);//如果要求直接打印,直接输出System.out.println(curr.val);// 将前驱节点的右子树连接到当前节点prev.right = curr;curr = curr.left;} else {// 前驱节点的右子树已经连接到当前节点,断开连接,输出当前节点,然后遍历右子树prev.right = null;curr = curr.right;}}}return res;}测试:
public static void main(String[] args) {TreeNode root = new TreeNode(1);root.left = new TreeNode(2);root.left.right = new TreeNode(5);root.left.right.right = new TreeNode(7);root.right = new TreeNode(3);root.left.left = new TreeNode(4);root.left.left.left = new TreeNode(6);System.out.println(preorderTraversal(root));}
还是这样一颗二叉树,输出如下:
[1, 2, 4, 6, 5, 7, 3]
四.后序Morris遍历
1.后序Morris遍历的思路
后序Morris遍历实现起来有一定的难度,但是基本代码还是不变,只是在打印的地方有略微的区别,
具体的思路如下:
1.初始化当前的结点为根结点
2.若当前的结点的左节点为空,则输出当前结点,然后遍历当前结点的右子树,即'curr=curr.right'
3.若当前结点的左节点不为空,则找到当前结点的前驱节点,即当前结点左节点的最右侧结点,记为'prev'
- 如果'prev.right''为空,然后将pre.right指向curr结点,然后遍历当前结点的左子树,即'curr=curr.left'
- 如果'prev.right''不为空,此时进行逆序存储,说明已经遍历完了当前节点的左子树,断开 `prev.right` 的连接,即'prev.left=null',然后遍历当前节点的右子树,即 `curr=curr.right`.
2.具体的代码实现
public List<Integer> postorderTraversal(TreeNode root) {List<Integer> res = new ArrayList<>();TreeNode dump = new TreeNode(0);//建立一个临时结点dump.left = root; //设置dump的左节点为rootTreeNode curr = dump; //当前节点为dumpwhile (curr != null) {if (curr.left == null) { // 左子树为空,则输出当前节点,然后遍历右子树curr = curr.right;} else {// 找到当前节点的前驱节点TreeNode prev = curr.left;while (prev.right != null && prev.right != curr) {prev = prev.right;}if (prev.right == null) {// 将前驱节点的右子树连接到当前节点prev.right = curr;curr = curr.left;} else {reverseAddNodes(curr.left, prev, res);// 前驱节点的右子树已经连接到当前节点,断开连接,输出当前节点,然后遍历右子树prev.right = null;curr = curr.right;}}}return res;}private void reverseAddNodes(TreeNode begin, TreeNode end, List<Integer> res) {reverseNodes(begin, end); //将begin到end的进行逆序连接TreeNode curr = end;while (true) {//将逆序连接后端begin到end添加res.add(curr.val);if (curr == begin)break;curr = curr.right;}reverseNodes(end, begin);//恢复之前的连接状态}/*** 将begin到end的进行逆序连接** @param begin* @param end*/private void reverseNodes(TreeNode begin, TreeNode end) {TreeNode prev = begin;TreeNode curr = prev.right;TreeNode post;while (prev != end) {post = curr.right;curr.right = prev;prev = curr;curr = post;}}测试:
public static void main(String[] args) {TreeNode root = new TreeNode(1);root.left = new TreeNode(2);root.left.right = new TreeNode(5);root.left.right.right = new TreeNode(7);root.right = new TreeNode(3);root.left.left = new TreeNode(4);root.left.left.left = new TreeNode(6);System.out.println(postorderTraversal(root));}还是这样一颗二叉树,输出如下:
[6, 4, 7, 5, 2, 3, 1]
相关文章:

树的前中后序的Morris遍历
目录 一.Morris遍历 1.什么是Morris遍历 2.基本思想 3.Morris遍历的优点和缺点 4.知识回顾----二叉树的线索化 二.中序Morris遍历 1.中序Morris遍历的分析 2.中序Morris遍历的思路 3.具体的代码实现 三.前序Morris遍历 1.前序Morris遍历的思路 2.具体的代码实现 四…...
到底什么是线程?线程与进程有哪些区别?
上一篇文章我们讲述了什么是进程,进程的基本调度 http://t.csdn.cn/ybiwThttp://t.csdn.cn/ybiwT 那么本篇文章我们将了解一下什么是线程?线程与进程有哪些区别?线程应该怎么去编程? 目录 http://t.csdn.cn/ybiwThttp://t.csdn…...

你真的知道如何系统高效地学习数据结构与算法吗?
文章目录前言:什么是数据结构?什么是算法?学习这个算法需要什么基础?学习的重点在什么地方?一些可以让你事半功倍的学习技巧1.边学边练,适度刷题2.多问、多思考、多互动3.打怪升级学习法4.知识需要沉淀&…...

Linux操作系统基础的常用命令
1,Linux简介Linux是一种自由和开放源码的操作系统,存在着许多不同的Linux版本,但它们都使用了Linux内核。Linux可安装在各种计算机硬件设备中,比如手机、平板电脑、路由器、台式计算机。1.1Linux介绍Linux出现于1991年,…...
Jasypt加密库基本使用方法
目录 1 Jasypt简介... 2 基础知识回顾... 3 Jasypt基本加密器... 4 JasyptPBE加密器... 5 Jasypt池化加密器... 6 Jasypt客户端工具... 7 JasyptSpringboot基本用法... 8 JasyptSpringboot自定义加密器... 9 JasyptSprin…...

C++并发编程之五 高级线程管理
文章目录5.1.1 线程池5.1.1 线程池 在前面我们引入了线程的通信和同步手段,那么为什么还要引入线程池呢? 线程池是一种管理多个线程的技术,它可以减少线程的创建和销毁的开销,提高并发性能。线程池中有一定数量的空闲线程&#x…...
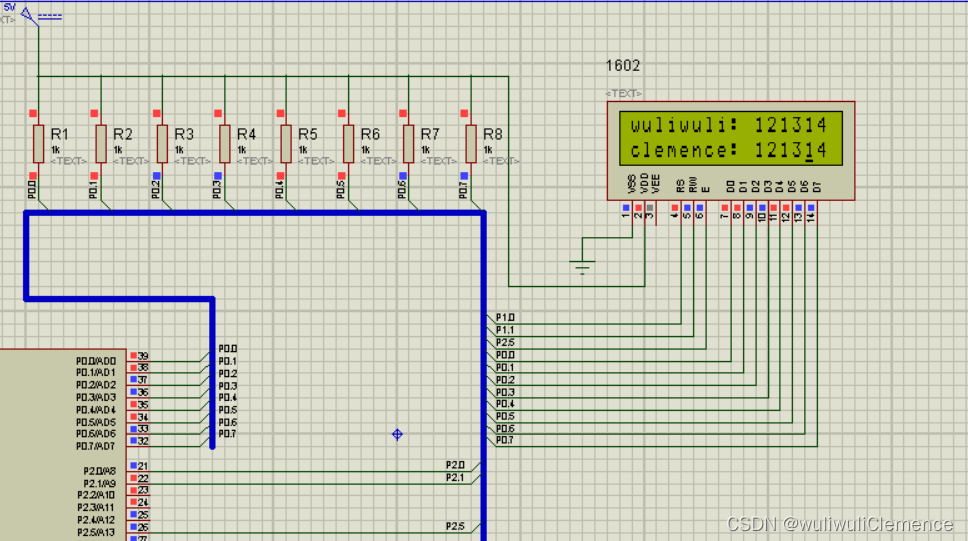
单片机——IIC协议与24C02
1、基础知识 1.1、IIC串行总线的组成及工作原理 I2C总线只有两根双向信号线。一根是数据线SDA,另一根是时钟线SCL。 1.2、I2C总线的数据传输 I2C总线进行数据传送时,时钟信号为高电平期间,数据线上的数据必须保持稳定,只有在时钟…...
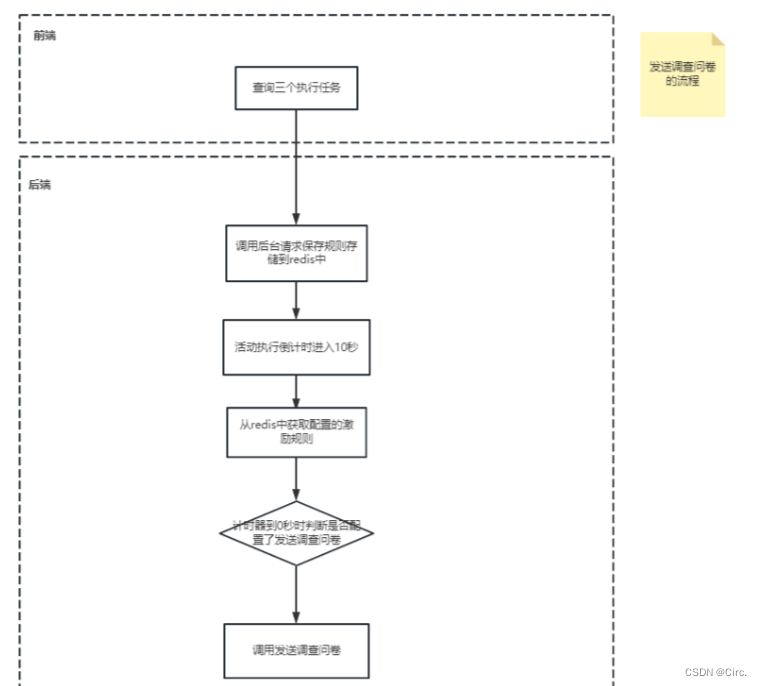
案例05-将不必要的逻辑放到前端(发送调查问卷)
目录一:背景介绍背景二:思路&方案重大问题:解决办法优点:三:总结一:背景介绍 本篇博客书写的意义是警示大家不必把不必要的逻辑放到前端。 明确前后端分离的意义。 背景 下面的主要逻辑是࿱…...
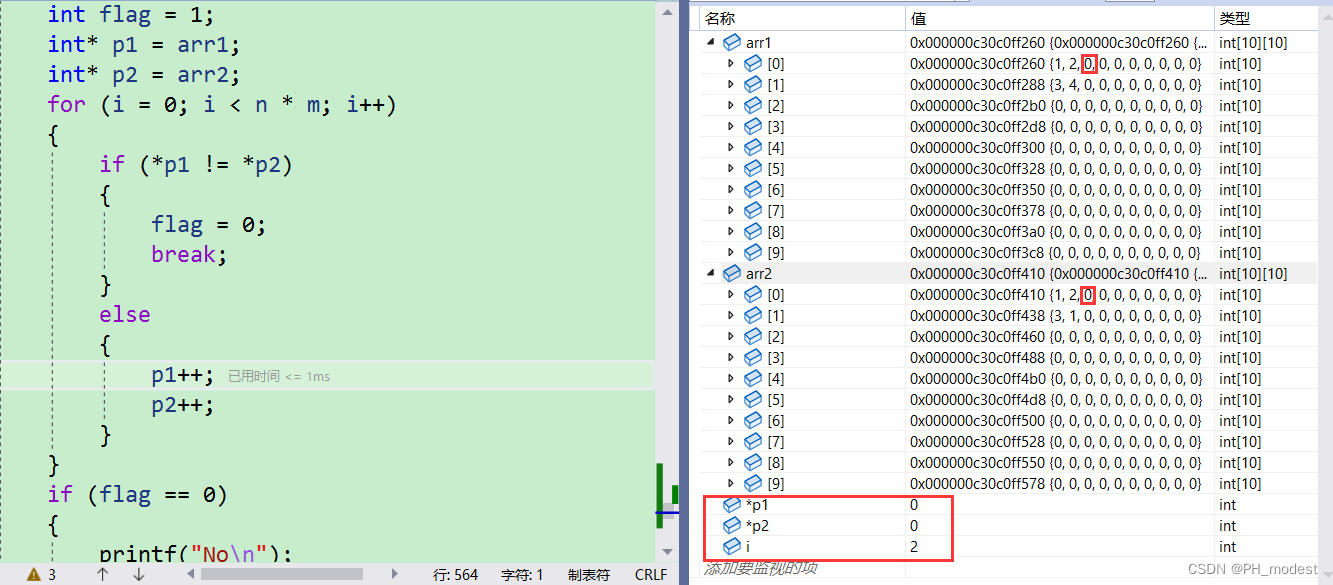
【每日一题】——矩阵相等判定
🌏博客主页:PH_modest的博客主页 🚩当前专栏:每日一题 💌其他专栏: 🔴 每日反刍 🟢 读书笔记 🟡 C语言跬步积累 🌈座右铭:广积粮,缓称…...
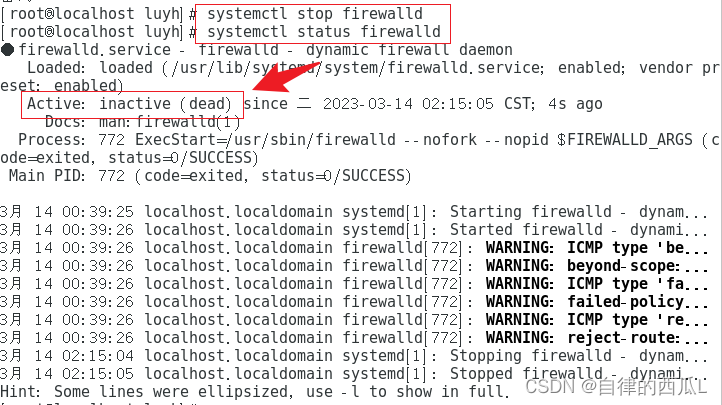
Linux防火墙的关闭
查看防火墙的状态打开终端输入如下命令systemctl status firewalld如图所示:running表示防火墙目前处于打开状态输入命令进行关闭防火墙:systemctl stop firewalld如图所示正常的用户是没有权限的,需要输入管理员的密码才能够进行关闭防火墙。…...
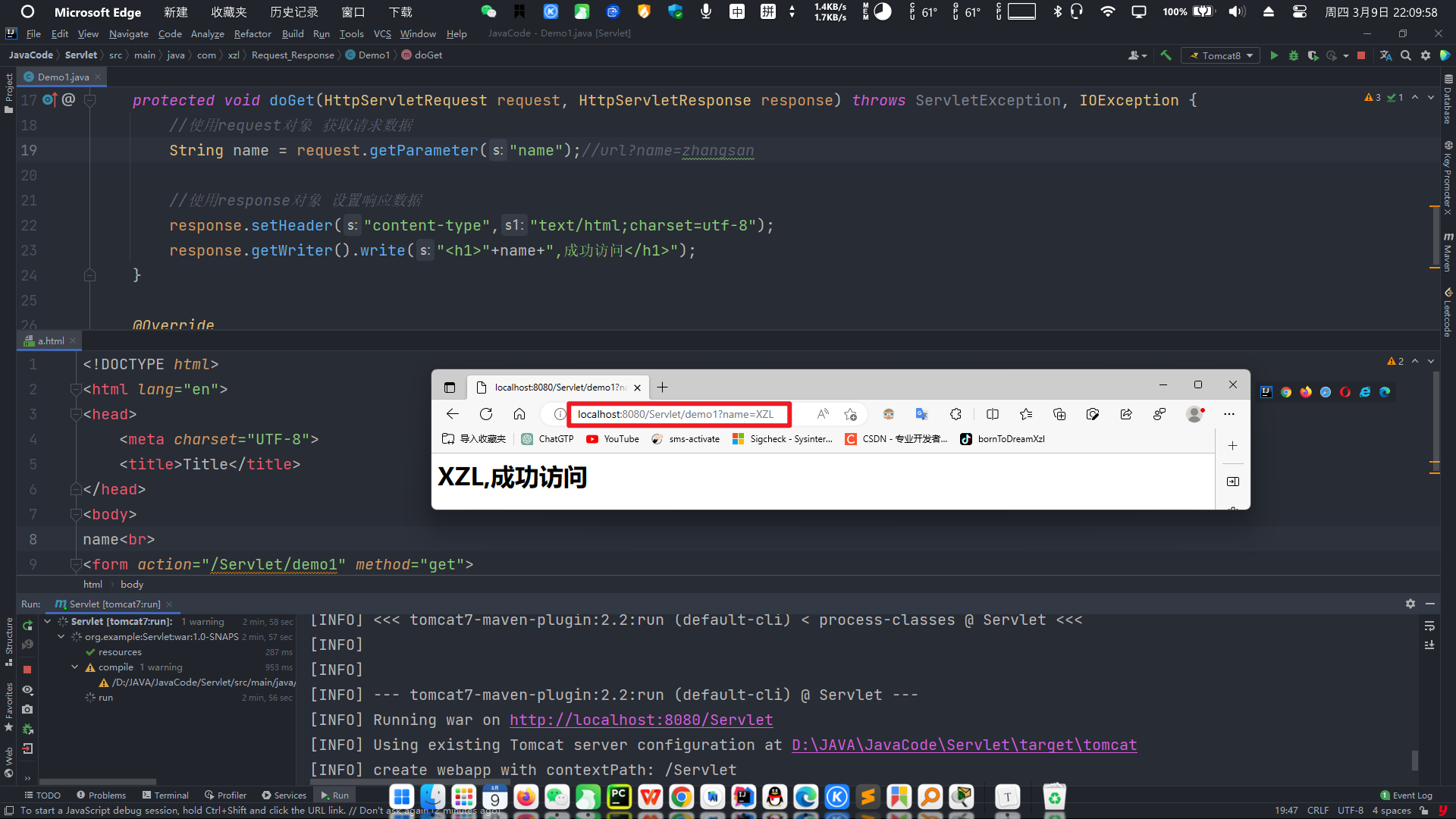
Request和Response的概述
⭐作者介绍:大二本科网络工程专业在读,持续学习Java,输出优质文章⭐作者主页:︶ㄣ释然⭐如果觉得文章写的不错,欢迎点个关注😉有写的不好的地方也欢迎指正,一同进步😁Request和Respo…...
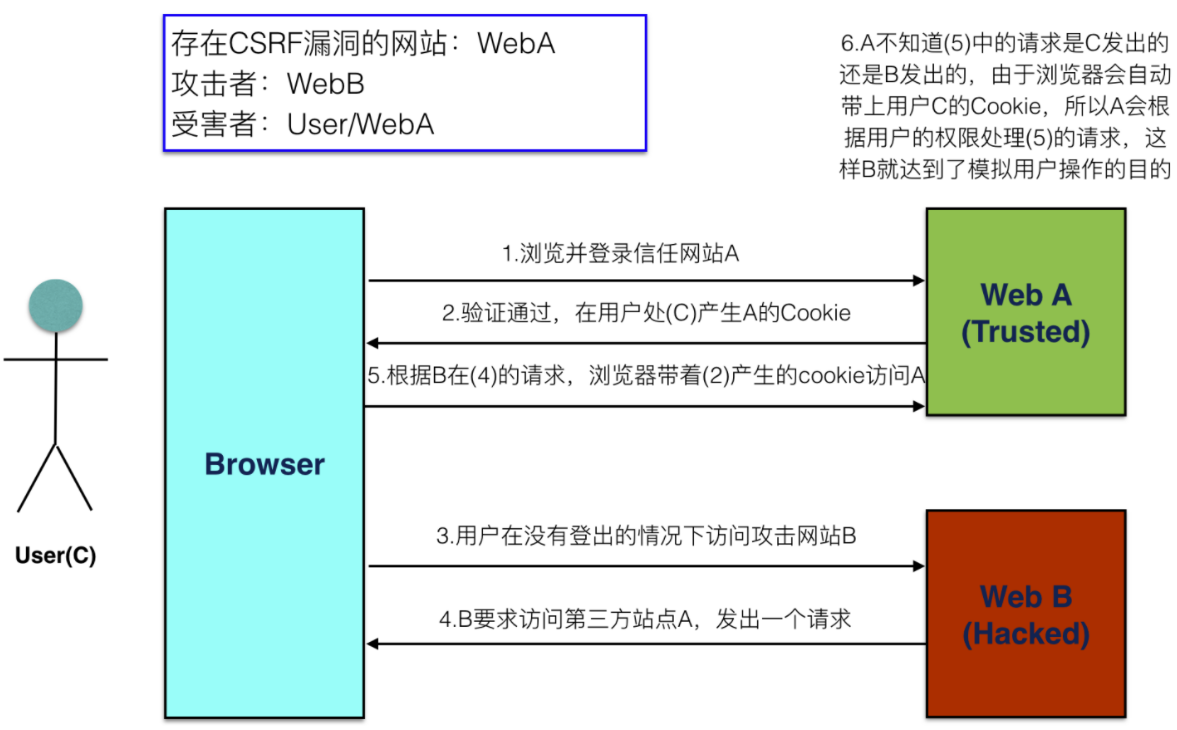
常见的Web安全漏洞:SYN攻击/CSRF/XSS
一、SYN攻击(属于DOS攻击) 什么情况下被动方出现SYN_RCVD状态?(flood攻击服务) 客户伪造 ip 端口, 向服务端发送SYN请求。完成2次握手,第三次服务端 等待客户端ACK确认,但由于客户不存在服务端一直未收到确认&#…...

【STC15单片机】 超声波模块的使用
目录 1 基于STC15F2K60S2的超声波测距代码 1.1 基本注意事项 1.1.1 跳线帽接法 1.1.2 晶振设置 1.2 板载超声波工作原理 1.2.1 原理总结 1.2.2 超声波代码思路 1.3 STC15单片机代码部分 1.3.1 定时器0&定时器1初始化 1.3.2 超声波ultrasonic.c ultrasonic.h文件配…...
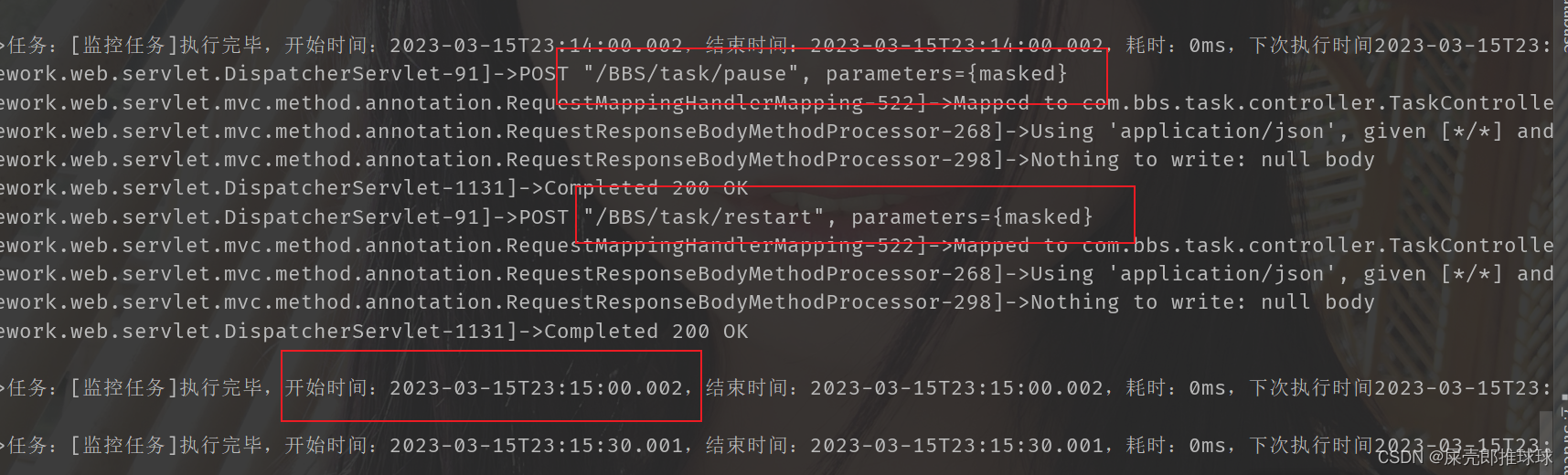
SpringBoot 动态操作定时任务(启动、停止、修改执行周期)增强版
前段时间编写了一篇博客SpringBoot 动态操作定时任务(启动、停止、修改执行周期,该篇博客还是帮助了很多同学。 但是该篇博客中的方法有些不足的地方: 只能通过前端控制器controller手动注册任务。【具体的应该是我们提前配置好我们的任务&am…...

快排函数 -- qsort函数(Quick Sort)
文章目录🔎1.qsort函数简介💡1.1.函数原型💡1.2.参数含义🔎2.比较函数介绍🔎3.比较函数使用案例💡3.1.整型数组💡3.2.浮点型数组💡3.3.结构体类型 - 字符串🔎4.利用冒泡排…...
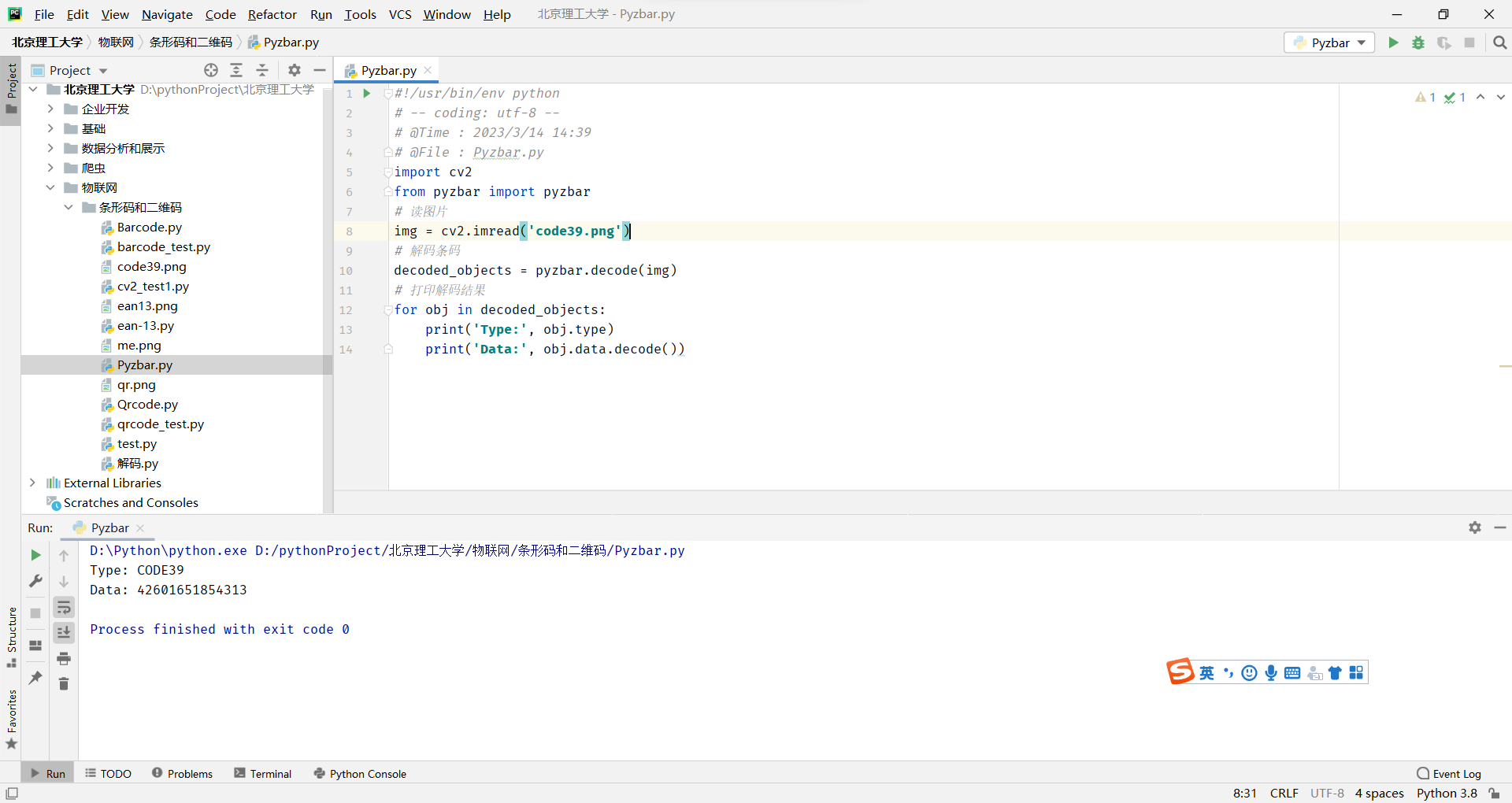
条形码和二维码
前言:需要的包的相关文档 1. Barcode:https://pypi.org/project/python-barcode/0.8.1/ 2. Qrcode:https://pypi.org/project/qrcode/ 3. Zbar: https://pypi.org/project/pyzbar/ 4. Opencv: https://docs.opencv.org/3.4.11/ 5. OpenC…...

大数据-学习实践-5企业级解决方案
大数据-学习实践-5企业级解决方案 (大数据系列) 文章目录大数据-学习实践-5企业级解决方案1知识点2具体内容2.1小文件问题2.1.1 SequenceFile2.1.2 MapFile2.1.3 小文件存储计算2.2数据倾斜2.3 YARN2.3.1 YARN架构2.3.2 YARN调度器2.3.2 YARN多资源队列配置和使用2.4Hadoop官方…...

破解吲哚花菁素IR-808 N3,IR-808 azide,IR-808叠氮,酯溶性染料修饰叠氮基团,相关知识
基础产品数据(Basic Product Data):CAS号:N/A中文名:IR-808叠氮英文名:IR-808 N3,IR-808 azideIR-808结构式(Structural):详细产品数据(Detailed …...
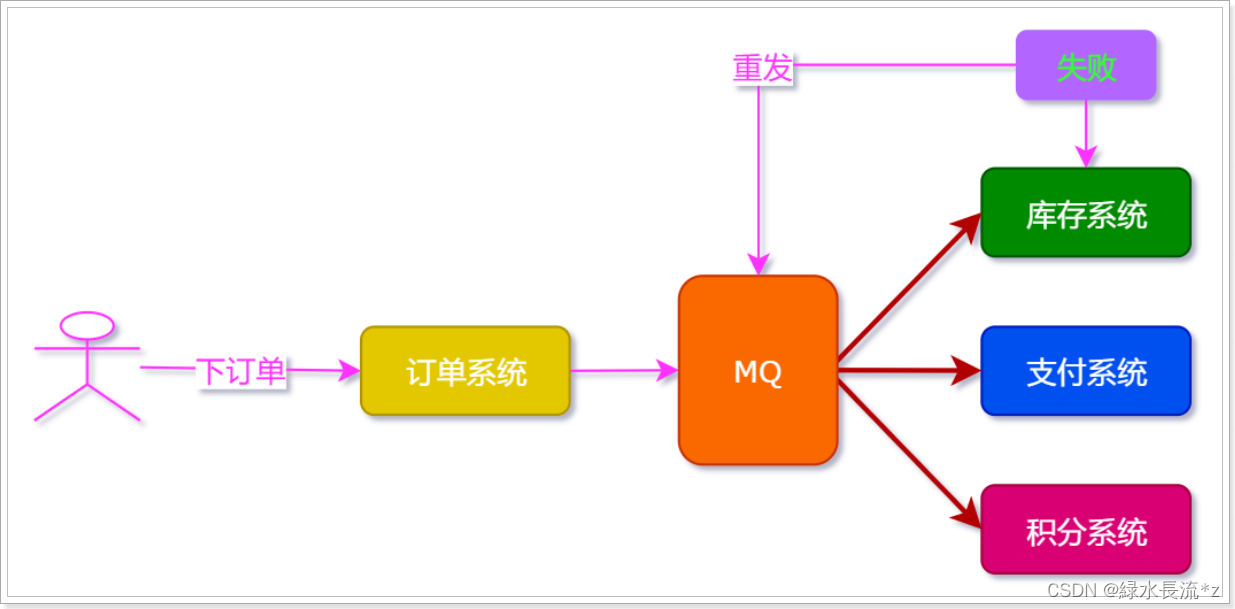
面试官:MQ的好处到底有哪些?
💗推荐阅读文章💗 🌸JavaSE系列🌸👉1️⃣《JavaSE系列教程》🌺MySQL系列🌺👉2️⃣《MySQL系列教程》🍀JavaWeb系列🍀👉3️⃣《JavaWeb系列教程》…...

事务机制:Redis能实现ACID属性吗?
ACID特性无需多言。我们知道关系数据库比如mysql可以实现事务的ACID特性,begin,commit,回滚实现。 那么redis可以实现ACID吗,结论是不能完全保证。 首先要知道redis通过MULTI关键字开启事务,中间一系列操作,加到操作队列中并不执…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...
