多层全连接神经网络(三)---分类问题
问题介绍
机器学习中的监督学习主要分为回归问题和分类问题,我们之前已经讲过回归问题了,它希望预测的结果是连续的,那么分类问题所预测的结果就是离散的类别。这时输入变量可以是离散的,也可以是连续的,而监督学习从数据中学习一个分类模型或者分类决策函数,它被称为分类器(classifier)。分类器对新的输入进行输出预测,这个过程即称为分类(classification)。例如,判断邮件是否为垃圾邮件,医生判断病人是否生病,或者预测明天天气是否下雨等。同时分类问题中包括有二分类和多分类问题我们下面先讲一下最著名的二分类算法---Logistic回归。首先从Logistic 回归的起源说起。
Logistic起源
Logistic 起源于对人口数量增长情况的研究,后来又被应用到了对于微生物生长情况的研究,以及解决经济学相关的问题,现在作为回归分析的一个分支来处理分类问题,先从 Logistic 分布人手,再由 Logistic 分布推出 Logistic 回归。
Logistic分布
设 X 是连续的随机变量,服从 Logistic 分布是指 X 的积累分布函数和密度函数如下:

其中 μ 影响中心对称点的位置,γ 越小中心点附近的增长速度越快。下一节会讲到在深度学习中常用的一个非线性变换 Sigmoid 函数是 Logistic 分布函数中 γ=1,μ=0 的特殊形式。

其函数图像如图 3.8 所示,由于函数很像“S”形,所以该函数又叫 Sigmoid 函数。

二分类的 Logistic 回归
Logistic 回归不仅可以解决二分类问题,也可以解决多分类问题,但是二分类问题最为常见同时也具有良好的解释性。对于二分类问题,Logistic 回归的目标是希望找到一个区分度足够好的决策边界,能够将两类很好地分开。
假设输入的数据的特征向量,那么决策边界可以表示为
;假设存在一个样本点使得
,那么可以判定它的类别是1;如果
,那么可以判定其类别是0。这个过程其实是一个感知机的过程,通过决策函数的符号来判断其属于哪一类。而 Logistic 回归要更进一步,通过找到分类概率 P(Y=1) 与输入变量x的直接关系,然后通过比较概率值来判断类别,简单来说就是通过计算下面两个概率分布:

其中w是权重、b是偏置。现在介绍 Logistic 模型的特点,先引入一个概念:一个事件发生的几率(odds)是指该事件发生的概率与不发生的概率的比值,比如一个事件发生的概率是p,那么该事件发生的几率是,该事件的对数几率或logit函数是:

对于 Logistic 回归而言,我们由式 (3.16) 和式 (3.17) 可以得到:

这也就是说在 Logistic 回归模型中,输出 Y=1 的对数几率是输入 x 的线性函数,这也就是 Logistic 回归名称的原因。如果观察式(3.17),则可以得到另外一种 Logistic 回归的定义,即线性函数的值越接近正无穷,概率值就越接近1;线性函数的值越接近负无穷,概率值越接近0。因此 Logistic 回归的思路是先拟合决策边界(这里的决策边界不局限于线性,还可以是多项式),在建立这个边界和分类概率的关系,从而得到二分类情况下的概率。
Logistic 回归的代码实现
首先我们打开txt文件,可以看到数据存放的方式,如图3.9所示

每个数据点是一行,每一行中前面两个数据表示 x 坐标和 y 坐标,最后一个数据表示其类别。
我们先从 data.txt 文件中读取数据,使用非常简单的 python 读取 txt 的方法就能够实现。
with open('data.txt', 'r') as f:data_list = f.readlines()data_list = [i.split('\n')[0] for i in data_list]data_list = [i.split(',') for i in data_list]data = [(float(i[0]), float(i[1]), float(i[2])) for i in data_list]然后通过matplotlib 能够简单地将数据画出来。
x0 = list(filter(lambda x: x[-1] == 0.0, data))
x1 = list(filter(lambda x: x[-1] == 1.0, data))
plot_x0_0 = [i[0] for i in x0]
plot_x0_1 = [i[1] for i in x0]
plot_x1_0 = [i[0] for i in x1]
plot_xl_1 = [i[1] for i in x1]plt.plot(plot_x0_0, plot_x0_1, 'ro', label='x_0')
plt.plot(plot_x1_0, plot_xl_1, 'bo', label='x_1')
plt.legend(loc='best')
# plt.show()首先将两个类别分开,然后将所有的数据点画出就能够得到图3.10。

从图3.10中我们可以明显看出这些数据点被分为两个类:一类用红色的点,一类用蓝色的点,我们希望通过 Logistic 回归将它们分开。
接下来定义 Logistic 回归的模型,以及二分类问题的损失函数和优化方法。
class LogisticRegression(nn.Module):def __init__(self):super(LogisticRegression, self).__init__()self.lr = nn.Linear(2, 1)self.sm = nn.Sigmoid()def forward(self, x):x = self.lr(x)x = self.sm(x)return xlogistic_model = LogisticRegression()
if torch.cuda.is_available():logistic_model.cuda()criterion = nn.BCELoss()
optimizer = torch.optim.SGD(logistic_model.parameters(), lr=1e-3, momentum=0.9)
这里 nn.BCELoss 是二分类的损失函数,torch.optim.SGD 是随机梯度下降优化函数。
然后训练模型,并且间隔一定的迭代次数输出结果。
x_data = [(float(i[0]), float(i[1])) for i in data_list]
y_data = [int(i[2]) for i in data_list] # Convert labels to binary (0 or 1)
for epoch in range(50000):if torch.cuda.is_available():x = Variable(torch.Tensor(x_data)).cuda()y = Variable(torch.Tensor(y_data)).cuda()else:x = Variable(torch.Tensor(x_data))y = Variable(torch.Tensor(y_data))# =================forward================out = logistic_model(x)y = y.unsqueeze(1)loss = criterion(out, y)print_loss = loss.item()mask = out.ge(0.5).float()correct = (mask == y).sum()acc = correct.item() / x.size(0)# =================backward===============optimizer.zero_grad()loss.backward()optimizer.step()if (epoch + 1) % 2000 == 0:print('*' * 10)print('epoch {}'.format(epoch + 1))print('loss is {:.4f}'.format(print_loss))print('acc is {:.4f}'.format(acc)) 其中 mask=out.ge(0.5).float() 是判断输出结果如果大于 0.5 就等于 1,小于 0.5 就等于 0,通过这个来计算模型分类的准确率。
训练完成我们可以得到图3.11所示的 loss 和准确率。因为数据相对简单,同时我们使用的是也是简单的线性 Logistic 回归,loss 已经降得相对较低,同时也有 91%的准确率

我们可以将这条直线画出来,因为模型中学习的参数 w1,w2 和 b 其实构成了一条直线 w1x+w2y+b=0,在直线上方是一类,在直线下方又是一类。我们可以通过下面的方式将模型的参数取出来,并将直线画出来,如图3.12所示
w0, w1 = logistic_model.lr.weight[0]
w0 = w0.item()
w1 = w1.item()
b = logistic_model.lr.bias.data[0].item()
plot_x = np.arange(30, 100, 0.1)
plot_y = (-w0 * plot_x - b) / w1
plt.plot(plot_x, plot_y)
plt.show()
通过图3.12我们可以看出这条直线基本上将这两类数据都分开了。
以上我们介绍了分类问题中的二分类问题和 Logistic 回归算法,一般来说,Logistic 回归也可以处理多分类问题,但最常见的还是应用在处理二分类问题上,下面我们将介绍一下使用神经网络算法来处理多分类问题。

相关文章:

多层全连接神经网络(三)---分类问题
问题介绍 机器学习中的监督学习主要分为回归问题和分类问题,我们之前已经讲过回归问题了,它希望预测的结果是连续的,那么分类问题所预测的结果就是离散的类别。这时输入变量可以是离散的,也可以是连续的,而监督学习从数…...

签名优化:请求数据类型不是`application/json`,将只对随机数进行签名计算,例如文件上传接口。
文章目录 I 签名进行请求数据类型类型判断1.1 常见的ContentType1.2 签名切面处理1.3 文件上传案例1.4 处理接口信息背景: 文件上传接口的请求数据类型通常为multipart/form-data,方便携带文本域和使用接口文档进行调试。 如果携带JSON数据,不方便调试接口。 前端数据也要特…...

PostgreSQL的Json数据类型如何使用
PostgreSQL中的JSON数据类型提供了一种灵活的方式来存储JSON(JavaScript Object Notation)数据。JSON是一种轻量级的数据交换格式,易于人阅读和编写,同时也易于机器解析和生成。在PostgreSQL中,你可以使用JSON和JSONB&…...

SpringData JPA Mongodb 查询部分字段
JPA 网上用的好像不多,找了好多材料以后最终找了这个可行的方案: Query(fields "{tender_id:1,_id:0}")List<MGPltTender> findByTenderIdIsNotNull(PageRequest pageRequest); 调用: Sort sort Sort.by(popularType.getC…...

NC65 设置下拉列表框值
NC65 设置下拉列表框值,如人员任职信息的异动事件: // 只有在入职登记时,才为异动事件下拉框过滤掉【离职】和【离职后变动】两个item DefaultConstEnum[] enumItems initTransevent(); BillItem item getBillCardPanel().getHeadItem(Psn…...

小阿轩yx-高性能内存对象缓存
小阿轩yx-高性能内存对象缓存 案例分析 案例概述 Memcached 是一款开源的高性能分布式内存对象缓存系统用于很多网站提高访问速度,尤其是需要频繁访问数据的大型网站是典型的 C/S 架构,需要构建 Memcached 服务器端与 Memcached API 客户端用 C 语言…...

华中师范大学学报人文社会科学版
一、《华中师范大学学报(人文社会科学版)》是国家教育部主管、华中师范大学主办的人文社会科学综合性学术期刊。本刊用稿以质量为标准,不分内稿外稿。文稿一经发表,即付报酬,不收版面费。 二、根据教育部和新闻出版总署颁发的社会科学学报编排规范,来稿应注意以下各项: 1. 题…...

CI/CD的node.js编译报错npm ERR! network request to https://registry.npmjs.org/
1、背景: 在维护paas云平台过程中,有研发反馈paas云平台上的CI/CD的前端流水线执行异常。 2、问题描述: 流水线执行的是前端编译,使用的是node.js环境。报错内容如下: 2024-07-18T01:23:04.203585287Z npm ERR! code E…...

用ssh tunnel的方式设置 AWS DocumentDB 公网访问
AWS DocumentDB的设定是只允许VPC内进行访问的,同时官方文档给了步骤,通过ssh tunnel的方式,可以从公网,或者从VPC外的网络,对DocumentDB进行访问。 我阅读了AWS官方文档并测试了这个步骤,如下是详细的步骤…...

基于电鸿(电力鸿蒙)的边缘计算网关,支持定制
1 产品信息 边缘计算网关基于平头哥 TH1520 芯片,支持 OpenHarmony 小型系统,是 连接物联网设备和云平台的重要枢纽,可应用于城市基础设施,智能工厂,智能建筑,营业网点,运营 服务中心相关场…...

WPF之URI的使用
pack://application:, pack://application:, 是一个在 WPF (Windows Presentation Foundation) 应用程序中用于指定资源位置的 URI (统一资源标识符) 方案的特定格式。这个格式用于访问嵌入在应用程序程序集(assemblies)中的资源,如图像、XA…...
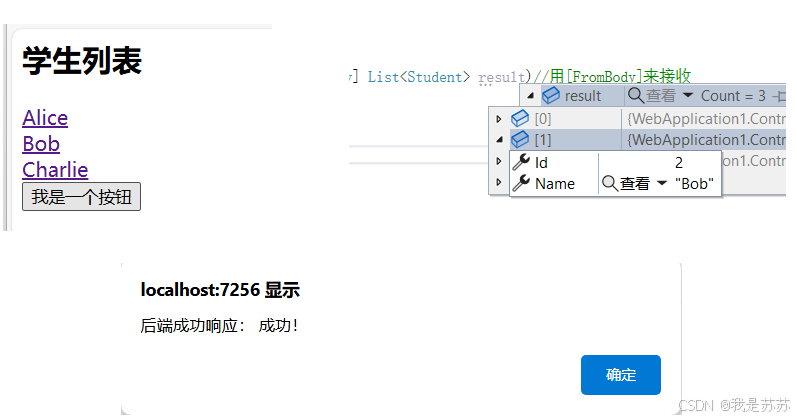
Web开发:ASP.NET CORE前后端交互之AJAX(含基础Demo)
目录 一、后端 二、前端 三、代码位置 四、实现效果 五、关键的点 1.后端传输给前端: 2.前端传输给后端 一、后端 using Microsoft.AspNetCore.Mvc; using Microsoft.AspNetCore.Mvc.RazorPages; using Microsoft.AspNetCore.Mvc.Rendering; using WebAppl…...

经典神经网络(14)T5模型原理详解及其微调(文本摘要)
经典神经网络(14)T5模型原理详解及其微调(文本摘要) 2018 年,谷歌发布基于双向 Transformer 的大规模预训练语言模型 BERT,而后一系列基于 BERT 的研究工作如春笋般涌现,预训练模型也成为了业内解决 NLP 问题的标配。 2019年,谷歌…...

C语言结构体字节对齐技术详解
C语言结构体字节对齐技术详解(第一部分) 在C语言中,结构体字节对齐是一个重要的概念,它涉及到内存中数据的布局和访问效率。字节对齐可以帮助提高程序的性能,减少内存碎片,并确保数据的一致性和正确性。本…...
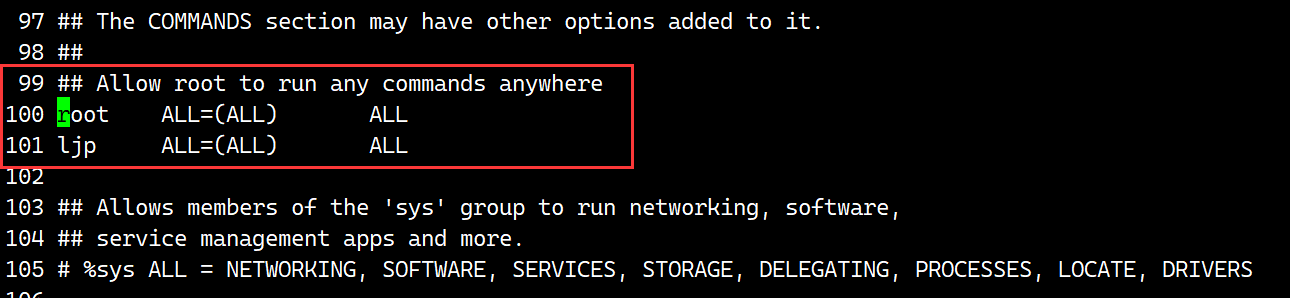
Linux编辑器——vim的使用
目录 vim的基本概念 命令模式 底行模式 插入模式 注释和取消注释 普通用户进行sudo提权 vim配置问题 vim的基本概念 一般使用的vim有三种模式: 命令模式 底行模式和插入模式,可以进行转换; vim filename 打开vim,进入的…...

Java案例斗地主游戏
目录 一案例要求: 二具体代码: 一案例要求: (由于暂时没有学到通信知识,所以只会发牌,不会设计打牌游戏) 二具体代码: Ⅰ:主函数 package three;public class test {…...

sqlite|轻量数据库|pgadmin4的sqlite数据库操作--重置密码和账号解锁
前言: pgadmin4的用户密码以及pgadmin4创建的pg数据库的连接信息等等都是存放在sqlite数据库内的;而有的时候,可能会由于自己的问题将pgadmin4的密码忘记,这个时候需要重置pgadmin4的密码,或者是pgadmin4的密码输错多…...

【ARMv8/v9 异常模型入门及渐进 9.1 - FIQ 和 IRQ 打开和关闭】
请阅读【ARMv8/v9 ARM64 System Exception】 文章目录 FIQ/IRQ Enable and Disable汇编指令详解功能解释使用场景和注意事项 FIQ/IRQ Enable and Disable 在ARMv8/v9架构中,可以使用下面汇编指令来打开FIQ和 IRQ,代码如下: asm volatile ("msr da…...

深入探索Flutter中的状态管理:使用Provider库
当涉及Flutter状态管理时,provider是一个强大且灵活的解决方案,它提供了一种简单且高效的方式来管理应用程序状态。本文将详细介绍Flutter中provider插件的使用方法、示例代码、各种使用场景以及注意事项。 1. 引入依赖 首先,需要在项目的pubspec.yaml文件中添加provider依…...
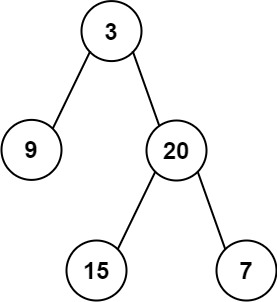
算法工程师第十四天(找树左下角的值 路径总和 从中序与后序遍历序列构造二叉树 )
参考文献 代码随想录 一、找树左下角的值 给定一个二叉树的 根节点 root,请找出该二叉树的 最底层 最左边 节点的值。 假设二叉树中至少有一个节点。 示例 1: 输入: root [2,1,3] 输出: 1示例 2: 输入: [1,2,3,4,null,5,6,null,null,7] 输出: 7 层次遍历&#…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...

第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10+pip3.10)
第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10pip3.10) 一:前言二:安装编译依赖二:安装Python3.10三:安装PIP3.10四:安装Paddlepaddle基础框架4.1…...

Kubernetes 节点自动伸缩(Cluster Autoscaler)原理与实践
在 Kubernetes 集群中,如何在保障应用高可用的同时有效地管理资源,一直是运维人员和开发者关注的重点。随着微服务架构的普及,集群内各个服务的负载波动日趋明显,传统的手动扩缩容方式已无法满足实时性和弹性需求。 Cluster Auto…...

智能职业发展系统:AI驱动的职业规划平台技术解析
智能职业发展系统:AI驱动的职业规划平台技术解析 引言:数字时代的职业革命 在当今瞬息万变的就业市场中,传统的职业规划方法已无法满足个人和企业的需求。据统计,全球每年有超过2亿人面临职业转型困境,而企业也因此遭…...

java高级——高阶函数、如何定义一个函数式接口类似stream流的filter
java高级——高阶函数、stream流 前情提要文章介绍一、函数伊始1.1 合格的函数1.2 有形的函数2. 函数对象2.1 函数对象——行为参数化2.2 函数对象——延迟执行 二、 函数编程语法1. 函数对象表现形式1.1 Lambda表达式1.2 方法引用(Math::max) 2 函数接口…...
