【算法基础】Dijkstra 算法
定义:
- g [ i ] [ j ] g[i][j] g[i][j] 表示 v i v_i vi 到 $v_j $的边权重,如果没有连接,则 g [ i ] [ j ] = ∞ g[i][j] = \infty g[i][j]=∞
- d i s [ i ] dis[i] dis[i] 表示 v k v_k vk 到节点 v i v_i vi 的最短长度, d i s [ k ] = 0 , d i s [ i ] = ∞ , i ≠ k dis[k] = 0, dis[i]=\infty, i \neq k dis[k]=0,dis[i]=∞,i=k.
目标:
- 计算出 d i s dis dis 数组,也就是任何点到 v k v_k vk 的距离。
step1 : 更新 v k v_k vk 的所有邻居节点 v y v_y vy的最短路径; 即: d i s [ y ] = g [ k ] [ y ] dis[y] = g[k][y] dis[y]=g[k][y]
step2 : 找出 这些邻居节点中路径最短的 d i s [ i 1 ] dis[i1] dis[i1]. 此时 d i s [ i 1 ] dis[i1] dis[i1] 一定已经是最短的了,可以用反证法来证明。
step3 : 找出 v i 1 v_{i1} vi1 的邻居节点 y ′ y' y′, 如果 d i s [ i 1 ] + g [ i 1 ] [ y ′ ] < d i s [ y ′ ] dis[i1]+g[i1][y'] < dis[y'] dis[i1]+g[i1][y′]<dis[y′], 则更新 d i s [ y ′ ] = d i s [ i 1 ] + g [ i 1 ] [ y ′ ] dis[y'] =dis[i1]+g[i1][y'] dis[y′]=dis[i1]+g[i1][y′], 否则不更新。
step4 : 找出 k , i 1 k,i1 k,i1之外的 d i s [ i ] dis[i] dis[i] 最小的值 d i s [ i 2 ] dis[i2] dis[i2], 重复之前的更新过程,知道取完所有点为止。
code :
leecode 743
朴素写法:
class Solution:def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:g = [[inf for _ in range(n)] for _ in range(n)] # 邻接矩阵for x, y, d in times:g[x - 1][y - 1] = ddis = [inf] * nans = dis[k - 1] = 0 # 起始节点done = [False] * n #是否确定为最短while True:x = -1# 找到最短的 done 是用来排除已经确定的那些点的。完成后x 记录当前最短距离的那个点。# 起始为 kfor i, ok in enumerate(done):if not ok and (x < 0 or dis[i] < dis[x]):x = i# 没有找到,也就是所有点已经全部确定后。if x < 0:return ans # 最后一次算出的最短路就是最大的# 无法到达if dis[x] == inf: # 有节点无法到达return -1# 因为每次都是递增的,而答案是要求最大的最短路径。ans = dis[x] # 求出的最短路会越来越大done[x] = True # 最短路长度已确定(无法变得更小)# 更新 x 的邻居节点的最短距离。for y, d in enumerate(g[x]):# 更新 x 的邻居的最短路dis[y] = min(dis[y], dis[x] + d)堆优化 Dijkstra:
class Solution:def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:g = [[] for _ in range(n)] # 邻接表for x, y, d in times:g[x - 1].append((y - 1, d))dis = [inf] * ndis[k - 1] = 0h = [(0, k - 1)] # 二元组 (dis[i], i)while h:dx, x = heappop(h) # 找到最短路径的 x 和其相应的 disif dx > dis[x]: # x 之前出堆过,continue# 这里continue 是因为 对于一个x 由于更新了多次dis, 堆中科恩那个存在多个 dx, 对于那些较大的dx, 不再使用的意思。# 更新邻居for y, d in g[x]:new_dis = dx + dif new_dis < dis[y]:dis[y] = new_dis # 更新 x 的邻居的最短路heappush(h, (new_dis, y))mx = max(dis)return mx if mx < inf else -1相关文章:

【算法基础】Dijkstra 算法
定义: g [ i ] [ j ] g[i][j] g[i][j] 表示 v i v_i vi 到 $v_j $的边权重,如果没有连接,则 g [ i ] [ j ] ∞ g[i][j] \infty g[i][j]∞ d i s [ i ] dis[i] dis[i] 表示 v k v_k vk 到节点 v i v_i vi 的最短长度, …...

使用 Flask 3 搭建问答平台(三):注册页面模板渲染
前言 前端文件下载 链接https://pan.baidu.com/s/1Ju5hhhhy5pcUMM7VS3S5YA?pwd6666%C2%A0 知识点 1. 在路由中渲染前端页面 2. 使用 JinJa 2 模板实现前端代码复用 一、auth.py from flask import render_templatebp.route(/register, methods[GET]) def register():re…...

pycharm如何debug for循环里面的错误值
一般debug时,在for循环里面的话,需要自己一步一步点。如果循环几百次那种就比较麻烦。此时可以采用try except的方式来解决 例子如下 #ptyhon debug for循环的代码 num[1,2,3,s,4] ans0 for i in num:try:ansiexcept:print(错误) print(ans) 结果如下&a…...

解决网页中的 video 标签在移动端浏览器(如百度访问网页)视频脱离文档流播放问题
问题现象 部分浏览器视频脱离文档流,滚动时,视频是悬浮出来,在顶部播放 解决方案 添加下列属性,可解决大部分浏览器的脱离文档流的问题 <videowebkit-playsinline""playsInlinex5-playsinlinet7-video-player-t…...

.Net--CLS,CTS,CLI,BCL,FCL
1.什么是CLS? 所以.NET专门为此参考每种语言(例如C# ,VB,F#)并找出了语言间的共性,然后定义了一组规则,开发者都遵守这个规则来编码,那么代码就能被任意.NET平台支持的语言所通用。 而与其说是规则&#x…...

Stable Diffusion:质量高画风清新细节丰富的二次元大模型二次元插图
今天和大家分享一个基于Pony模型训练的二次元模型:二次元插图。关于该模型有4个不同的分支版本。 1.5版本:loar模型,推荐底模型niji-动漫二次元4.5。 xl版本:SDXL模型版本 mix版本:光影减弱,减少SDXL版本…...

数读MEME之争:以太坊获更高价值共识,抢占热点成Solana流量密码
在当前显著的加密牛市中,以太坊和Solana之间的竞争不仅在币价表现上显而易见,生态发展方面也备受关注。特别是在这轮MEME行情中,双方阵营的MEME代币呈现出不同的特点和趋势。 市场表现对比 以太坊的优势: 市场份额和认可度更高&…...

python的with语句
1.with语句的作用 在 Python 中,with 语句用于创建一个上下文管理器,以更简洁和安全的方式管理资源。 其主要优点是可以确保在代码块执行完毕后,相关资源能够被正确释放或清理,即使在代码块内部发生了异常。 以下是一个使用 with…...

Selenium原理深度解析
在自动化测试领域,Selenium无疑是最受欢迎和广泛使用的工具之一。它支持多种浏览器和操作系统,为开发人员和测试人员提供了强大的自动化测试解决方案。本文将深入探讨Selenium的工作原理,包括其架构、核心组件、执行流程以及它在自动化测试中…...

算法复杂度<数据结构 C版>
什么是算法复杂度? 简单来说算法复杂度是用来衡量一个算法的优劣的,一个程序在运行时,对运行时间和运行空间有要求,即时间复杂度和空间复杂度。 目录 什么是算法复杂度? 大O的渐近表达式 时间复杂度示例 空间复杂度…...

【XSS】
文章目录 0x01 简介0x02 XSS Payload用法XSS攻击平台及调试JavaScript 0x03 XSS绕过XSS漏洞防御策略 跨站脚本攻击,Cross Site Script。(重点在于脚本script) 有关XSS可以造成的 危害,见 0x02 XSS Payload用法 分类 反射型、存储…...
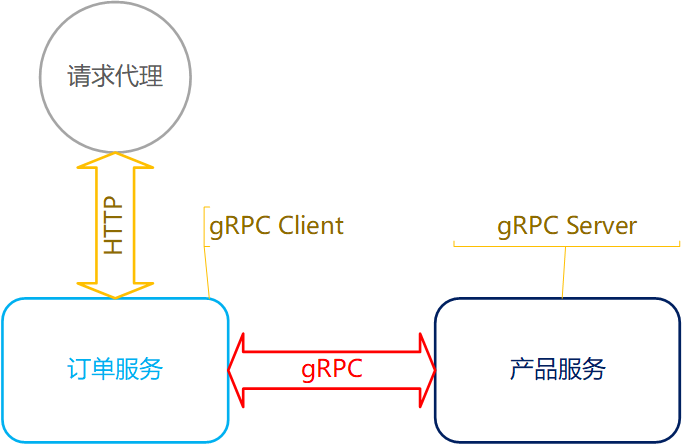
Go网络编程-RPC程序设计
gRPC 通信 RPC 介绍 RPC, Remote Procedure Call,远程过程调用。与 HTTP 一致,也是应用层协议。该协议的目标是实现:调用远程过程(方法、函数)就如调用本地方法一致。 如图所示: 说明: Servi…...

Linux 性能优化:轻松入门
文章目录 前言一、磁盘性能优化1、 磁盘 RAID 模式选择2、文件系统优化 二、优化 CPU1、性能监控 :2、进程优先级调整 :3、进程与 CPU 绑定 : 三、优化内存四、网络性能优化1、调整 TCP 缓冲区大小2、修改系统级别的文件描述符的数量3、调整 …...

C++相关概念和易错语法(22)(final、纯虚函数、继承多态难点)
1.final final在继承和多态中都可以使用,在继承中是指不想将自己被继承,在多态中是指不想该函数被重写,比较简单,下面是一些使用例子。 2.纯虚函数 当我们需要抽象一个类的时候,我们就需要用到纯虚函数。所谓抽象的类…...

状态管理的艺术:探索Flutter的Provider库
状态管理的艺术:探索Flutter的Provider库 前言 上一篇文章中,我们详细介绍了 Flutter 应用中的状态管理,以及 StatefulWidget 和 setState 的使用。 本篇我们继续介绍另一个实现状态管理的方式:Provider。 Provider优缺点 基…...

玩转HarmonyOS NEXT之IM应用首页布局
本文从目前流行的垂类市场中,选择即时通讯应用作为典型案例详细介绍HarmonyOS NEXT的各类布局在实际开发中的综合应用。即时通讯应用的核心功能为用户交互,主要包含对话聊天、通讯录,社交圈等交互功能。 应用首页 创建一个包含一列的栅格布…...
GPT-4o大语言模型优化、本地私有化部署、从0-1搭建、智能体构建
原文链接:GPT-4o大语言模型优化、本地私有化部署、从0-1搭建、智能体构建https://mp.weixin.qq.com/s?__bizMzUzNTczMDMxMg&mid2247608565&idx3&snd4e9d447efd82e8dd8192f7573886dab&chksmfa826912cdf5e00414e01626b52bab83a96199a6bf69cbbef7f7fe…...
记录些MySQL题集(4)
1、数据库的三范式是什么? 第一范式:列不可再分 第二范式:在第一范式的基础上,要求数据库表中的所有非主键列完全依赖于主键,而不是仅依赖于主键的一部分 第三范式:满足第二范式的基础上,所有…...
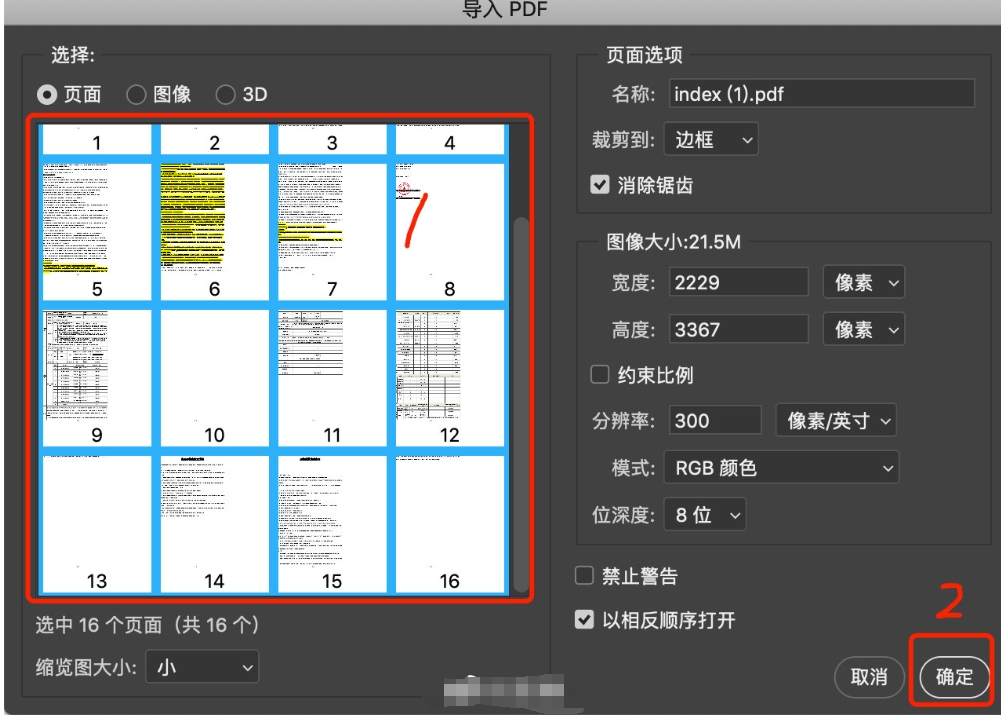
pdf提取其中一页怎么操作?提取PDF其中一页的方法
pdf提取其中一页怎么操作?需要从一个PDF文件中提取特定页码的操作通常是在处理文档时常见的需求。这种操作允许用户选择性地获取所需的信息,而不必操作整个文档。通过选择性提取页面,你可以更高效地管理和利用PDF文件的内容,无论是…...

godot使用ws
go服务端 package mainimport ("encoding/json""fmt""github.com/gorilla/websocket""net/http" )var upgrader websocket.Upgrader{ReadBufferSize: 1024,WriteBufferSize: 1024, }// 处理函数 func handleWebSocket(w http.Respo…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

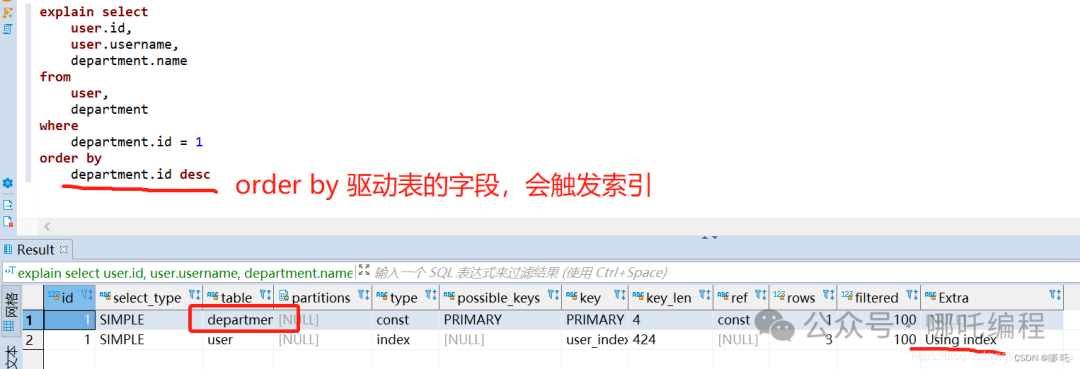
【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...
