概率论原理精解【4】
文章目录
- 度量空间
- 概述
- 理论基础
- 定义
- 特点
- 高级概念
- 广泛应用
- 性质
- 例子
- 应用
- 柯西数列
- 柯西数列的定义
- 柯西数列的例子
- 参考文献
度量空间
概述
- 设 f : R n → R m , f ˙ ( x ) 在 { x : ∣ x − x 0 ∣ < r } 内连续,则当 ∣ t ∣ < r 时, f:R^n\rightarrow R^m,\dot f(x)在\{x:|x-x_0|<r\}内连续,则当|t|<r时, f:Rn→Rm,f˙(x)在{x:∣x−x0∣<r}内连续,则当∣t∣<r时,
f ( x 0 + t ) = f ( x 0 ) + ∫ 0 1 f ˙ ( x 0 + u t ) d u ⋅ t f(x_0+t)=f(x_0)+\int_0^1\dot f(x_0+ut)du \cdot t f(x0+t)=f(x0)+∫01f˙(x0+ut)du⋅t - A与B是两个集合,A与B不对等,而与B的某个子集对等,A的势小于B的势, A ≺ B A \prec B A≺B
- 集合 A 、 B ,若 ∀ A 0 ⊂ A , ∀ B 0 ⊂ B , s . t . A ∼ B 0 , B ∼ A 0 , 则 A ∼ B 集合A、B,若\forall A_0 \subset A,\forall B_0 \subset B, s.t. A \sim B_0,B \sim A_0,则A \sim B 集合A、B,若∀A0⊂A,∀B0⊂B,s.t.A∼B0,B∼A0,则A∼B
- 任何无限集都包含一个可数子集.
- 可数集的子集如果不是有限集就是可数集。
- A 有限 B 可数,则 A ∪ B 可数 A有限B可数,则 A\cup B 可数 A有限B可数,则A∪B可数
- A 和 B 可数,则 A ∪ B 可数 A和B可数,则 A\cup B 可数 A和B可数,则A∪B可数
- 不是可数集的无限集称为不可数集
- 离散度量空间
X 为非空集合, ∀ x , y ∈ X , ρ ( x , y ) = { 0 if x = y 1 if x ≠ y X为非空集合,\forall x,y \in X,\rho(x,y)= \begin{cases} 0 &\text{if } x=y \\ 1 &\text{if } x \ne y \end{cases} X为非空集合,∀x,y∈X,ρ(x,y)={01if x=yif x=y - 有界函数空间
给定集合 A , F ( A ) 表示 A 上有界实值或复值函数全体, 对于 F ( A ) 上的任意两个元素(两点或两个函数),定义度量 ρ ( x , y ) = s u p t ∈ A ∣ x ( t ) − y ( t ) ∣ 给定集合A,F(A)表示A上有界实值或复值函数全体, \\对于F(A)上的任意两个元素(两点或两个函数),定义度量 \\\rho(x,y)=sup_{t \in A}|x(t)-y(t)| 给定集合A,F(A)表示A上有界实值或复值函数全体,对于F(A)上的任意两个元素(两点或两个函数),定义度量ρ(x,y)=supt∈A∣x(t)−y(t)∣ - 连续函数空间 C [ a , b ] 连续函数空间 C[a,b] 连续函数空间C[a,b]
C [ a , b ] 表示闭区间 [ α , b ] 上的实值 ( 或复值 ) 连续函数全体, 对 C [ a , b ] 中任意两个元素(两点或两个函数)定义度量 C[a,b] 表示闭区间 [α,b] 上的实值(或复值)连 续函数全体, \\对 C[a,b] 中任意两个元素(两点或两个函数)定义度量 C[a,b]表示闭区间[α,b]上的实值(或复值)连续函数全体,对C[a,b]中任意两个元素(两点或两个函数)定义度量
ρ ( x , y ) = m a x a ≤ t ≤ b ∣ x ( t ) − y ( t ) ∣ \rho(x,y)=max_{a \le t \le b}|x(t)-y(t)| ρ(x,y)=maxa≤t≤b∣x(t)−y(t)∣ - 实数空间 R
R 中任意两点 x , y 定义度量 R中任意两点x,y定义度量 R中任意两点x,y定义度量
ρ ( x , y ) = ∣ x − y ∣ \rho(x,y)=|x-y| ρ(x,y)=∣x−y∣
理论基础
以下内容由文心一言自动生成
度量空间(Metric Space)是数学中的一个重要概念,它指的是一个集合,并且该集合中的任意元素之间的距离是可定义的。这种空间是现代数学中一种基本的、重要的、最接近于欧几里得空间的抽象空间。下面将从度量空间的定义、性质、例子以及应用等方面进行详细介绍。
定义
度量空间是由一个集合M和一个映射d组成的二元组(M, d),其中M是非空集合,d是M上的二元函数,称为度量(或距离)。这个映射d需要满足以下三个条件(高权威来源:百度百科):
- 正定性:对于任意x, y ∈ M,有d(x, y) ≥ 0,且d(x, y) = 0当且仅当x = y。
- 对称性:对于任意x, y ∈ M,有d(x, y) = d(y, x)。
- 三角不等式:对于任意x, y, z ∈ M,有d(x, z) ≤ d(x, y) + d(y, z)。
满足以上三个条件的二元组(M, d)被称为一个度量空间,或者称M为一个对于度量d而言的度量空间。
特点
当然,我们可以继续深入探讨度量空间的一些高级概念和它在更广泛领域的应用。
高级概念
-
完备度量空间:
一个度量空间是完备的,如果它中的每个柯西序列都收敛到该空间中的一个点。实数集R和复数集C都是完备度量空间,但有理数集Q则不是。 -
等距映射(Isometry):
如果两个度量空间(M, d)和(N, ρ)之间存在一个双射函数f: M → N,且对于所有的x, y ∈ M,都有d(x, y) = ρ(f(x), f(y)),则称f为从M到N的等距映射。等距映射保持度量空间的所有度量性质。 -
度量空间的开球和闭球:
对于度量空间 ( M , d ) 中的点 p 和正实数 r , 点 p 的 r − 邻域(或开球)定义为 B r ( p ) = x ∈ M ∣ d ( x , p ) < r 。 类似地,闭球是 B ˉ r ( p ) = x ∈ M ∣ d ( x , p ) ≤ r 。 对于度量空间(M, d)中的点p和正实数r, \\点p的r-邻域(或开球)定义为B_r(p) = {x ∈ M | d(x, p) < r}。 \\类似地,闭球是B̄_r(p) = {x ∈ M | d(x, p) ≤ r}。 对于度量空间(M,d)中的点p和正实数r,点p的r−邻域(或开球)定义为Br(p)=x∈M∣d(x,p)<r。类似地,闭球是Bˉr(p)=x∈M∣d(x,p)≤r。 -
度量空间的稠密子集和可分性:
如果度量空间M的子集A在M中稠密,那么M中的每个非空开集都包含A中的点。如果M有一个可数稠密子集,则称M是可分的。 -
度量空间的嵌入:
如果度量空间(M, d)可以等距地嵌入到另一个度量空间(N, ρ)中,即存在一个等距映射f: M → N,则称M可以嵌入到N中。
广泛应用
-
计算机科学:
度量空间在数据挖掘、机器学习、模式识别、信息检索等领域有重要应用。例如,通过定义数据点之间的距离,可以使用聚类算法(如K-means)、分类算法(如K-最近邻)等来处理和分析数据。 -
物理学:
在物理学中,度量空间用于描述物理空间和时间,如广义相对论中的时空结构。此外,度量空间也用于量子力学中的态空间,其中量子态之间的距离定义了它们之间的相似度。 -
生物学:
在生物信息学中,度量空间用于比较和分析生物序列(如DNA、RNA和蛋白质序列)的相似性。通过定义序列之间的距离度量,可以识别出序列之间的进化关系或功能相似性。 -
经济学和金融学:
度量空间在金融工程中用于评估金融产品的风险和回报。例如,通过定义资产之间的距离度量,可以计算资产组合的风险和相关性,从而进行投资组合优化和风险管理。 -
数学分析:
度量空间是数学分析中的基础工具,用于研究函数的性质、极限、连续性和可微性等。在泛函分析中,度量空间上的函数空间和算子理论是研究函数空间拓扑结构和线性算子性质的重要工具。
总之,度量空间是现代数学和应用数学中一个极其重要的概念,它在数学理论、计算机科学、物理学、生物学、经济学和金融学等多个领域都有广泛的应用。通过对度量空间的深入研究,我们可以更好地理解和解决这些领域中的各种问题。
性质
度量空间具有一系列重要的性质,包括但不限于:
- 紧性、可数紧性、序列紧性、子集紧性在度量空间中是一致的。
- 可分性、遗传可分性、第二可数性、林德勒夫性在度量空间中也是一致的。
- 度量空间必满足第一可数公理,是豪斯多夫空间、完全正规空间、仿紧空间。
例子
度量空间的例子非常丰富,以下是一些常见的例子:
- 欧几里得空间:在n维欧几里得空间中, 两点 x = ( x 1 , x 2 , . . . , x n ) 和 y = ( y 1 , y 2 , . . . , y n ) 之间的距离定义为 d ( x , y ) = [ ( x 1 − y 1 ) 2 + ( x 2 − y 2 ) 2 + . . . + ( x n − y n ) 2 两点x = (x_1, x_2, ..., x_n)和y = (y_1, y_2, ..., y_n)之间的距离定义为d(x, y) = \sqrt {[(x_1 - y_1)^2 + (x_2 - y_2)^2 + ... + (x_n - y_n)^2} 两点x=(x1,x2,...,xn)和y=(y1,y2,...,yn)之间的距离定义为d(x,y)=[(x1−y1)2+(x2−y2)2+...+(xn−yn)2。
- 离散度量空间:在离散度量空间中,任意两点x和y之间的距离定义为d(x, y) = 0(如果x = y)或d(x, y) = 1(如果x ≠ y)。
- 函数空间:例如,考虑定义在闭区间[0, 1]上的所有连续实值函数的集合,可以定义两个函数f和g之间的距离为它们之间上确界距离,即d(f, g) = sup |f(x) - g(x)|,其中x ∈ [0, 1]。
应用
度量空间在数学和应用数学中有着广泛的应用,包括但不限于:
- 调和分析:调和函数与热核理论、Riesz变换及函数空间理论是调和分析的重要组成部分,这些理论在偏微分方程、几何分析及数学物理等方向都有着重要的应用。
- 函数空间理论:度量空间上的函数空间理论是研究函数性质的重要工具,例如在分析学、泛函分析等领域中都有广泛应用。
- 几何分析:度量空间为研究几何对象的性质提供了有力的工具,例如在研究流形、曲面等几何对象时,度量空间的概念和性质都是不可或缺的。
综上所述,度量空间是现代数学中一个基本而重要的概念,它在数学和应用数学的多个领域中都有着广泛的应用。
柯西数列
柯西数列的定义
柯西数列(Cauchy sequence)是数学中的一个重要概念,特别是在度量空间(metric space)的上下文中。一个数列(或序列) { x n } \{x_n\} {xn}被称为柯西数列,如果对于任意的正实数 ϵ \epsilon ϵ(无论它有多小),都存在一个正整数 N N N,使得对于所有 m , n > N m, n > N m,n>N,都有 d ( x m , x n ) < ϵ d(x_m, x_n) < \epsilon d(xm,xn)<ϵ。这里, d ( x m , x n ) d(x_m, x_n) d(xm,xn)表示数列中第 m m m项和第 n n n项之间的距离,它依赖于度量空间中的距离函数(或度量)。
简单来说,柯西数列是一个“逐渐靠近”的数列,即随着项数的增加,数列中的任意两项之间的距离可以变得任意小。
柯西数列的例子
以下内容由文心一言自动生成
-
实数空间中的有理数数列:
考虑一个逼近无理数(如 2 \sqrt{2} 2)的有理数数列。例如,数列 { 1 , 3 2 , 7 5 , 17 12 , … } \left\{1, \frac{3}{2}, \frac{7}{5}, \frac{17}{12}, \ldots\right\} {1,23,57,1217,…},其中每一项都是 2 \sqrt{2} 2的某个有理数近似值,且越来越精确。这个数列在实数空间中是一个柯西数列,尽管它的极限(即 2 \sqrt{2} 2)是一个无理数,不在有理数集中。然而,在实数集(一个完备度量空间)中,这个数列确实有极限。 -
复数空间中的数列:
在复数空间中,也可以定义柯西数列。例如,考虑数列 { 1 , 1 + 1 i , 1 + 1 i + 1 i 2 , 1 + 1 i + 1 i 2 + 1 i 3 , … } \left\{1, 1 + \frac{1}{i}, 1 + \frac{1}{i} + \frac{1}{i^2}, 1 + \frac{1}{i} + \frac{1}{i^2} + \frac{1}{i^3}, \ldots\right\} {1,1+i1,1+i1+i21,1+i1+i21+i31,…},其中 i i i是虚数单位。这个数列实际上是在逼近复数 1 + 1 1 − i = 1 + 1 + i 2 = 3 2 + 1 2 i 1 + \frac{1}{1 - i} = 1 + \frac{1 + i}{2} = \frac{3}{2} + \frac{1}{2}i 1+1−i1=1+21+i=23+21i。在复数空间中,这也是一个柯西数列。 -
p-adic数域中的数列:
在更抽象的数学领域中,如p-adic数域(其中p是一个素数),也可以定义柯西数列。然而,这些数列的性质和实数或复数空间中的数列可能有所不同,因为p-adic数域中的距离函数和度量与实数或复数空间中的不同。
注意:在给出具体例子时,需要明确数列所在的度量空间以及该空间中的距离函数(或度量)。在不同的度量空间中,即使是相同的数列也可能不是柯西数列。此外,即使一个数列在某个度量空间中不是柯西数列,它也可能在另一个度量空间中成为柯西数列。
参考文献
1.《测度论基础与高等概率论》
2. 文心一言
相关文章:

概率论原理精解【4】
文章目录 度量空间概述理论基础定义特点高级概念广泛应用 性质例子应用 柯西数列柯西数列的定义柯西数列的例子 参考文献 度量空间 概述 设 f : R n → R m , f ˙ ( x ) 在 { x : ∣ x − x 0 ∣ < r } 内连续,则当 ∣ t ∣ < r 时, f:R^n\righ…...
Linux云计算 |【第一阶段】ENGINEER-DAY3
主要内容: LVM逻辑卷管理、VDO、RAID磁盘阵列、进程管理 一、新建逻辑卷 1、什么是逻辑卷 逻辑卷(Logical Volume)是逻辑卷管理(Logical Volume Management,LVM)系统中的一个概念。LVM是一种用于磁盘管理…...

springboot 实体类加注解校验入参数据
导入的是springboot自身的依赖包 import org.springframework.validation.annotation.Validated; import org.springframework.web.bind.annotation.*; import javax.validation.Valid;...

关于 Qt输入法在arm特定的某些weston下出现调用崩溃 的解决方法
若该文为原创文章,转载请注明原文出处 本文章博客地址:https://hpzwl.blog.csdn.net/article/details/140423667 长沙红胖子Qt(长沙创微智科)博文大全:开发技术集合(包含Qt实用技术、树莓派、三维、OpenCV…...

Android Studio关于Gradle及JDK问题解决
1.Android Studio 版本如:Android Studio Koala | 2024.1.1 2.Gradle 版本为:8.7 3.JDK 版本为:17 以上这三个必须匹配,具体可以看官网Android Studio 版本说明(https://developer.android.google.cn/studio?hlzh-…...

Leetcode 205. 同构字符串
205. 同构字符串 Leetcode 205. 同构字符串 一、题目描述二、我的想法三、其他人的题解 一、题目描述 给定两个字符串 s 和 t ,判断它们是否是同构的。 如果 s 中的字符可以按某种映射关系替换得到 t ,那么这两个字符串是同构的。 每个出现的字符都应…...

多口适配器,给您的生活增添便利
随着科技的快速发展,我们的生活已离不开各种各样的电子设备,智能手机、平板电脑、智能手表、无线耳机……它们共同构建了我们丰富多彩的数字生活。然而,面对众多设备的充电需求,传统的单一充电口已难以满足现代人的使用习惯。在这…...

探索现代Web开发:WebKit的剪贴板API革新
探索现代Web开发:WebKit的剪贴板API革新 在当今的Web开发领域,用户体验的提升是开发者们不懈追求的目标。其中一个关键的交互点便是剪贴板操作,它允许用户在网页与本地系统之间复制和粘贴数据。WebKit,作为Safari、QQ浏览器等众多…...

【电路笔记】-放大器的频率响应
放大器的频率响应 文章目录 放大器的频率响应1、概述2、定义3、电容器的影响4、低频响应5、高频响应6、总结1、概述 对于任何电子电路来说,放大器的行为都会受到其输入端子上信号频率的影响。 该特性称为频率响应。 频率响应是放大器最重要的特性之一。 在放大器设计的频率范…...

Artix7系列FPGA实现SDI视频编解码,基于GTP高速接口,提供3套工程源码和技术支持
目录 1、前言工程概述免责声明 2、相关方案推荐本博已有的 SDI 编解码方案本方案在Xilinx--Kintex系列FPGA上的应用本方案在Xilinx--Zynq系列FPGA上的应用 3、详细设计方案设计原理框图SDI 输入设备Gv8601a 均衡器GTP 高速接口-->解串与串化SMPTE SD/HD/3G SDI IP核BT1120转…...

NET 语言识别,语音控制操作、语音播报
System.Speech. 》》System.Speech.Synthesis; 语音播报 》》System.Speech.Recognition 语音识别 using System; using System.Collections.Generic; using System.ComponentModel; using System.Data; using System.Drawing; using System.Linq; using System.Speech.Recog…...

Unity 调试死循环程序
如果游戏出现死循环如何调试呢。 测试脚本 我们来做一个测试。 首先写一个死循环代码: using System.Collections; using System.Collections.Generic; using UnityEngine;public class dead : MonoBehaviour {void Start(){while (true){int a 1;}}}Unity对象设…...

视频监控平台LntonCVS视频融合共享平台智慧安防视频监控汇聚应用方案
LntonCVS是一款功能强大且灵活部署的安防视频监控平台。它支持多种主流标准协议,包括GB28181、RTSP/Onvif、RTMP等,同时能够兼容海康Ehome、海大宇等厂家的私有协议和SDK接入。该平台不仅提供传统的安防监控功能,还支持接入AI智能分析&#x…...
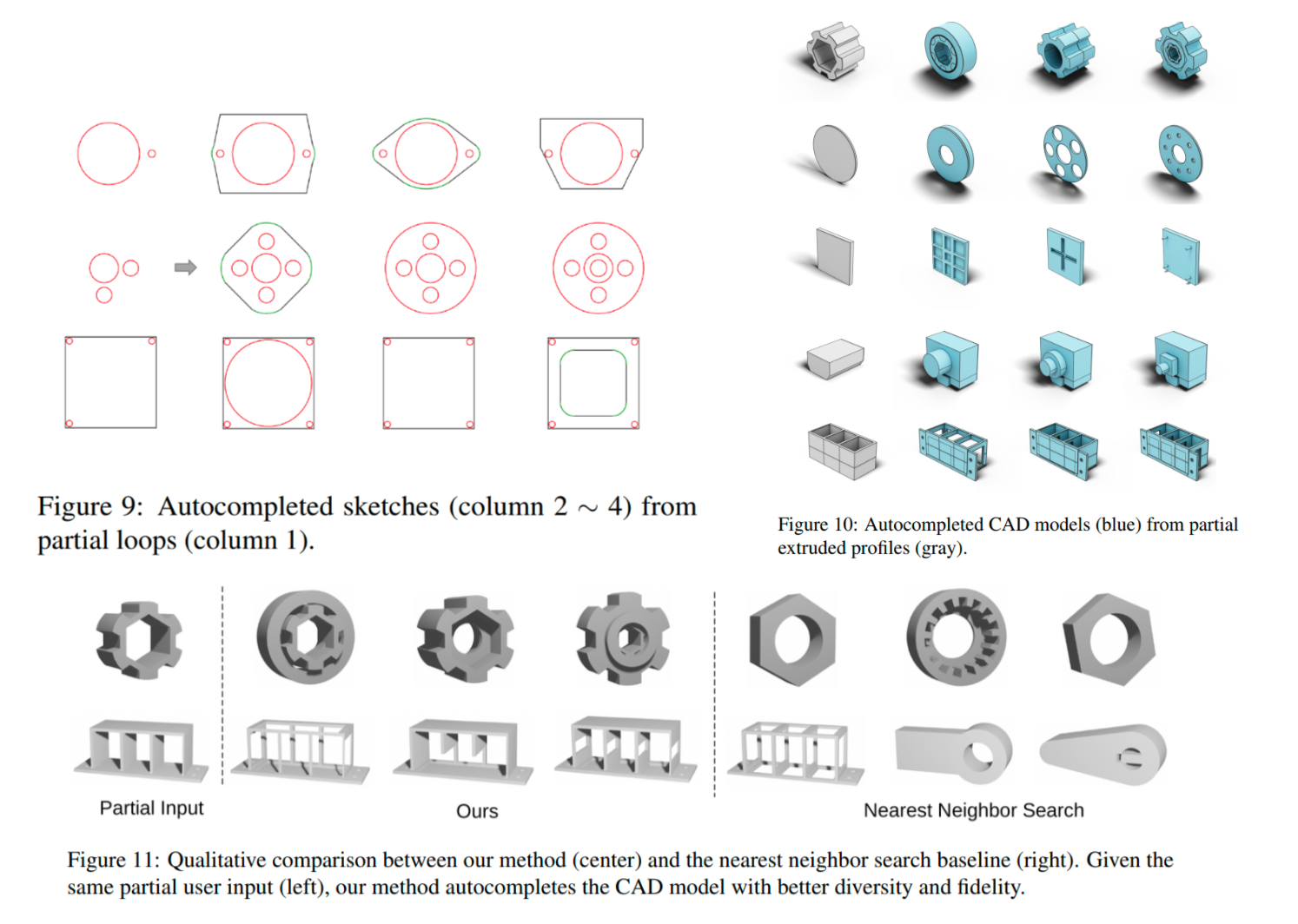
【论文阅读笔记】Hierarchical Neural Coding for Controllable CAD Model Generation
摘要 作者提出了一种CAD的创新生成模型,该模型将CAD模型的高级设计概念表示为从全局部件排列到局部曲线几何的三层神经代码的层级树,并且通过指定目标设计的代码树来控制CAD模型的生成或完成。具体而言,一种带有“掩码跳过连接”的向量量化变…...

Unity扩展SVN命令
可以直接在unity里右键文件提交和查看提交记录 顶部菜单栏上回退和更新整个unity工程 SvnForUnity.CS 记得要放在Editor文件夹下 using System.Collections; using System.Collections.Generic; using System.Diagnostics; using System.IO; using UnityEditor; using Unity…...
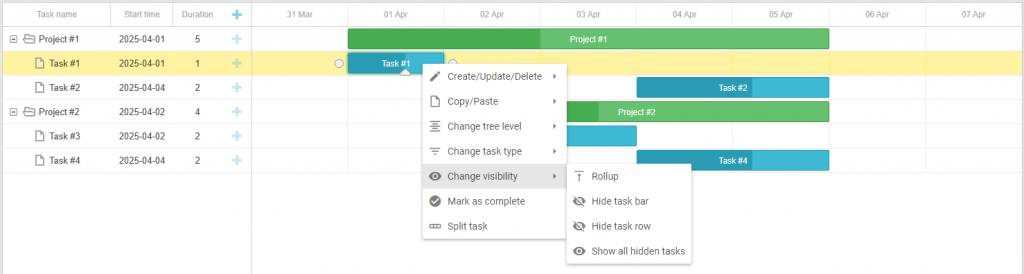
「实战应用」如何用DHTMLX将上下文菜单集成到JavaScript甘特图中(三)
DHTMLX Gantt是用于跨浏览器和跨平台应用程序的功能齐全的Gantt图表。可满足项目管理应用程序的所有需求,是最完善的甘特图图表库。 DHTMLX Gantt是一个高度可定制的工具,可以与项目管理应用程序所需的其他功能相补充。在本文中您将学习如何使用自定义上…...

微服务保护
1、什么是微服务保护 微服务保护是指在微服务架构中采取的一系列措施,以确保各个服务的稳定性、可靠性和安全性。微服务是一种将应用程序作为一套小服务开发的方法,每个服务运行在其独立的进程中,并通常围绕特定的业务能力进行构建。微服务保…...

Python语言的优势所在
Python语言具有多个显著的优势,这些优势使得它在软件开发、数据分析、机器学习、Web开发等众多领域广受欢迎。以下是Python语言的一些主要优势: 简单易学:Python的语法清晰简洁,接近自然语言,易于理解和编写。对于初学…...

npm install时报错 reason: certificate has expired
在VS code中导入新项目,执行npm install时报错: npm warn old lockfile Could not fetch metadata for antv/g3.4.10 FetchError: request to https://registry.npm.taobao.org/antv%2fg failed, reason: certificate has expirednpm warn old lockfile …...
价格战再起:OpenAI 发布更便宜、更智能的 GPT-4o Mini 模型|TodayAI
OpenAI 今日推出了一款名为 GPT-4o Mini 的新模型,这款模型较轻便且成本更低,旨在为开发者提供一个经济实惠的选择。与完整版模型相比,GPT-4o mini 在成本效益方面表现卓越,价格仅为每百万输入 tokens 15 美分和每百万输出 tokens…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...
