数据结构(二叉树-1)
文章目录
一、树
1.1 树的概念与结构
1.2 树的相关术语
1.3 树的表示
二、二叉树
2.1 二叉树的概念与结构
2.2特殊的二叉树
满二叉树
完全二叉树
2.3 二叉树的存储结构
三、实现顺序结构二叉树
3.1 堆的概念与结构
3.2 堆的实现
Heap.h
Heap.c
默认初始化堆
堆的销毁
堆的插入
删除堆顶数据
一、树
1.1 树的概念与结构
- 树是⼀种⾮线性的数据结构,它是由 n(n>=0) 个有限结点组成⼀个具有层次关系的集合。把它叫做 树是因为它看起来像⼀棵倒挂的树,也就是说它是根朝上,⽽叶朝下的。
- 有⼀个特殊的结点,称为根结点,根结点没有前驱结点。
- 除根结点外,其余结点被分成 M(M>0) 个互不相交的集合 T1、T2、……、Tm ,其中每⼀个集合 Ti(1 <= i <= m) ⼜是⼀棵结构与树类似的⼦树。每棵⼦树的根结点有且只有⼀个前驱,可以有 0 个或多个后继。因此,树是递归定义的。

树形结构中,⼦树之间不能有交集,否则就不是树形结构
- ⼦树是不相交的(如果存在相交就是图了,图以后得课程会有讲解)
- 除了根结点外,每个结点有且仅有⼀个⽗结点
- ⼀棵N个结点的树有N-1条边
1.2 树的相关术语
- ⽗结点/双亲结点:若⼀个结点含有⼦结点,则这个结点称为其⼦结点的⽗结点; 如上图:A是B的⽗结点
- ⼦结点/孩⼦结点:⼀个结点含有的⼦树的根结点称为该结点的⼦结点; 如上图:B是A的孩⼦结点
- 结点的度:⼀个结点有⼏个孩⼦,他的度就是多少;⽐如A的度为6,F的度为2,K的度为0
- 树的度:⼀棵树中,最⼤的结点的度称为树的度; 如上图:树的度为 6
- 叶⼦结点/终端结点:度为 0 的结点称为叶结点; 如上图: B、C、H、I... 等结点为叶结点
- 分⽀结点/⾮终端结点:度不为 0 的结点; 如上图: D、E、F、G... 等结点为分⽀结点
- 兄弟结点:具有相同⽗结点的结点互称为兄弟结点(亲兄弟); 如上图: B、C 是兄弟结点结点的层次:从根开始定义起,根为第 1 层,根的⼦结点为第 2 层,以此类推;
- 树的⾼度或深度:树中结点的最⼤层次; 如上图:树的⾼度为 4
- 结点的祖先:从根到该结点所经分⽀上的所有结点;如上图: A 是所有结点的祖先
- 路径:⼀条从树中任意节点出发,沿⽗节点-⼦节点连接,达到任意节点的序列;⽐如A到Q的路径为:A-E-J-Q;H到Q的路径H-D-A-E-J-Q
- ⼦孙:以某结点为根的⼦树中任⼀结点都称为该结点的⼦孙。如上图:所有结点都是A的⼦孙
- 森林:由 m(m>0) 棵互不相交的树的集合称为森林;
1.3 树的表示
孩⼦兄弟表⽰法:
struct TreeNode{struct Node* child; // 左边开始的第⼀个孩⼦结点struct Node* brother; // 指向其右边的下⼀个兄弟结点int data; // 结点中的数据域};二、二叉树
2.1 二叉树的概念与结构
- ⼆叉树不存在度⼤于 2 的结点
- ⼆叉树的⼦树有左右之分,次序不能颠倒,因此⼆叉树是有序树

2.2特殊的二叉树
满二叉树
⼀个⼆叉树,如果每⼀个层的结点数都达到最⼤值,则这个⼆叉树就是满⼆叉树。也就是说,如果⼀个⼆叉树的层数为 K ,且结点总数是 2 k − 1 ,则它就是满⼆叉树。

完全二叉树
完全⼆叉树是效率很⾼的数据结构,完全⼆叉树是由满⼆叉树⽽引出来的。对于深度为 K 的,有 n 个结点的⼆叉树,当且仅当其每⼀个结点都与深度为K的满⼆叉树中编号从 1 ⾄ n 的结点⼀⼀对应时称之为完全⼆叉树。要注意的是满⼆叉树是⼀种特殊的完全⼆叉树。
(假设二叉树层次为 k ,除了第 k 层外,每层结点的个数达到最大结点数,第 k 层结点个数不一定达到最大结点数)

2.3 二叉树的存储结构
- 顺序结构存储就是使⽤数组来存储,⼀般使⽤数组只适合表⽰完全⼆叉树,因为不是完全⼆叉树会有空间的浪费,完全⼆叉树更适合使⽤顺序结构存储。

三、实现顺序结构二叉树
3.1 堆的概念与结构
小根堆 大根堆


- 堆中某个结点的值总是不⼤于或不⼩于其⽗结点的值;
- 堆总是⼀棵完全⼆叉树。
- 对于具有 n 个结点的完全⼆叉树,如果按照从上⾄下从左⾄右的数组顺序对所有结点从0 开始编号,则对于序号为 i 的结点有:
- 若 i>0 , i 位置结点的双亲序号: (i-1)/2 ; i=0 , i 为根结点编号,⽆双亲结点
- 若 2i+1<n ,左孩⼦序号: 2i+1 , 2i+1>=n 否则⽆左孩⼦
- 若 2i+2<n ,右孩⼦序号: 2i+2 , 2i+2>=n 否则⽆右孩⼦
3.2 堆的实现
以小根堆为例子:
Heap.h
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>//定义堆的结构---数组typedef int HPDataType;typedef struct Heap
{HPDataType* arr;int size;//有效的数据个数int capacity;//空间大小
}HP;//初始化
void HPInit(HP* php);//销毁
void HPDestroy(HP* php);//堆的插入
void HPPush(HP* php, HPDataType x);//出堆,删除堆顶数据
void HPPop(HP* php);//返回堆顶数据
HPDataType HPTop(HP* php);// 判空
bool HPEmpty(HP* php);Heap.c
默认初始化堆
void HPInit(HP* php)
{assert(php);php->arr = NULL;php->capacity = php->size = 0;
}堆的销毁
void HPDestroy(HP* php)
{assert(php);if (php->arr){free(php->arr);php->arr = NULL;php->capacity = php->size - 0;}
}堆的插入

如果要在下一个数据 “50” 到 arr【6】的位置上就不满足小堆的特性,
此时我们就要用到:堆的向上调整算法
void swap(int* x, int* y)
{int z = *x;*x = *y;*y = z;
}void Adjustup(HPDataType* arr, int child)
{int parent = (child - 1) / 2;while (child > 0){if (arr[child] < arr[parent]) //如果插入的数据大小小于他的父节点{swap(&arr[child], &arr[parent]); //交换child = parent; //交换后的孩结点来到原来他的父节点的位置 parent = 2 * child - 1;}else{break;}}
}void HPPush(HP* php, HPDataType x)
{assert(php);//判断空间是否足够if (php->size == php->capacity){//扩容int newcapacity = php->capacity == 0 ? 4 : 2 * php->capacity;HPDataType* tmp = (HPDataType*)realloc(php->arr, newcapacity * sizeof(HPDataType));if (tmp == NULL){perror("realloc fail!");exit(1);}php->arr = tmp;php->capacity = newcapacity;}php->arr[php->size] = x;php->size++;Adjustup(php->arr, php->size - 1);
} 

删除堆顶数据

如果直接删除 arr【0】,就会改变原先堆的结构,所以我么可以先先将头和尾的数据交换,在删除 arr【5】,但是又有问题出现。交换删除后的数据有可能不满足小堆的特性,此时就要用到:堆的向下调整算法
void AdjustDown(HPDataType* arr, int parent, int n)
{int child = parent * 2 + 1; //左孩子while (child < n) //这里注意循环的条件{//找左右孩子中找最小的if (child + 1 < n && arr[child] > arr[child + 1]){child++;}if (arr[child] < arr[parent]){swap(&arr[child], &arr[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}void HPPop(HP* php)
{assert(php && php->size);//arr[0] arr[size-1]swap(&php->arr[0], &php->arr[php->size - 1]);php->size--;AdjustDown(php->arr, 0, php->size);}

test.c
最后测试一下代码的实现
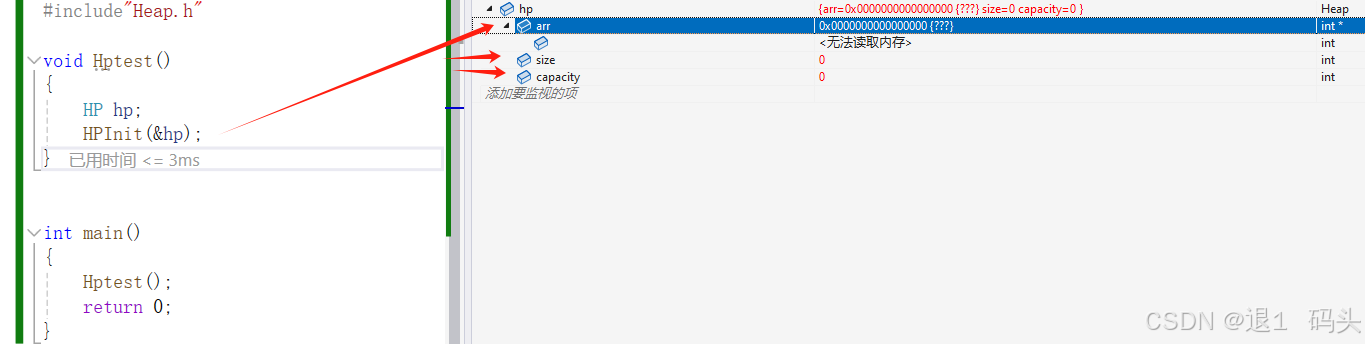
#include"Heap.h"void Hptest()
{HP hp;HPInit(&hp);int arr[] = { 17,25,60,54,30,70 };for (int i = 0; i < 6; i++){HPPush(&hp, arr[i]);}HPPop(&hp);
}int main()
{Hptest();return 0;
}
未完待续~
相关文章:

数据结构(二叉树-1)
文章目录 一、树 1.1 树的概念与结构 1.2 树的相关术语 1.3 树的表示 二、二叉树 2.1 二叉树的概念与结构 2.2特殊的二叉树 满二叉树 完全二叉树 2.3 二叉树的存储结构 三、实现顺序结构二叉树 3.1 堆的概念与结构 3.2 堆的实现 Heap.h Heap.c 默认初始化堆 堆的销毁 堆的插入 …...

巴黎奥运会倒计时 一个非常不错的倒计时提醒
巴黎奥运会还有几天就要开幕了,大家应该到处都可以看到巴黎奥运会的倒计时,不管是电视上,还是网络里,一搜索奥运会,就会看到。倒计时其实是一个我们在生活中很常用的一个方法,用来做事情的提醒,…...

【Python】使用库 -- 详解
库就是别人已经写好了的代码,可以让我们直接拿来用。 一个编程语言能不能流行起来,一方面取决于语法是否简单方便容易学习,一方面取决于生态是否完备。所谓的 “生态” 指的就是语言是否有足够丰富的库,来应对各种各样的场景。在…...
Web3D:WebGL为什么在渲染性能上输给了WebGPU。
WebGL已经成为了web3D的标配,市面上有N多基于webGL的3D引擎,WebGPU作为挑战者,在渲染性能上确实改过webGL一头,由于起步较晚,想通过这个优势加持,赶上并超越webGL仍需时日。 贝格前端工场为大家分享一下这…...
SpringBoot面试高频总结01
1. 什么是SpringBoot? SpringBoot是一个基于Spring框架的快速开发框架,它采用约定大于配置,自动装配的方式,可以快速地创建独立的,生产级别的,基于Spring的应用程序。 相比于传统的Spring框架,S…...
:概念与实现)
Linux 工作队列(Workqueue):概念与实现
目录 一、工作队列的概念1.1 什么是工作队列1.2 为什么使用工作队列 二、工作队列的实现2.1 定义和初始化工作队列2.2 工作队列API 三、工作队列的应用3.1 延迟执行任务3.2 处理复杂的中断任务 四、工作队列的类型4.1 普通工作队列4.2 高优先级工作队列 五、总结 在Linux内核中…...

前端页面是如何禁止被查看源码、被下载,被爬取,以及破解方法
文章目录 1.了解禁止查看,爬取原理1.1.JS代码,屏蔽屏蔽键盘和鼠标右键1.2.查看源码时,通过JS控制浏览器窗口变化2.百度文库是如何防止抓包2.1.HTPPS2.2. 动态加载为什么看不到?如何查看动态加载的内容?3.禁止复制,如果解决3.1.禁止复制原理3.2.如何破解1.了解禁止查看,爬…...

51单片机嵌入式开发:14、STC89C52RC 之HX1838红外解码NEC+数码管+串口打印+LED显示
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 STC89C52RC 之HX1838红外解码NEC数码管串口打印LED显示 STC89C52RC 之HX1838红外解码NEC数码管串口打印LED显示1 概述2 硬件电路2.1 遥控器2.2 红外接收器电路2.3 STC89C52单…...

在不同环境中,Java应用程序和MySQL等是如何与Docker进行交互和操作的?
1. 本地开发环境 在本地开发环境中,可以使用Docker Compose来管理和运行Java应用程序容器和MySQL容器。通常,会创建一个docker-compose.yml文件,定义需要的服务及其配置。 以下是一个示例docker-compose.yml文件: version: 3 services:app…...
《DRL》P10-P15-损失函数-优化(梯度下降和误差的反向传播)
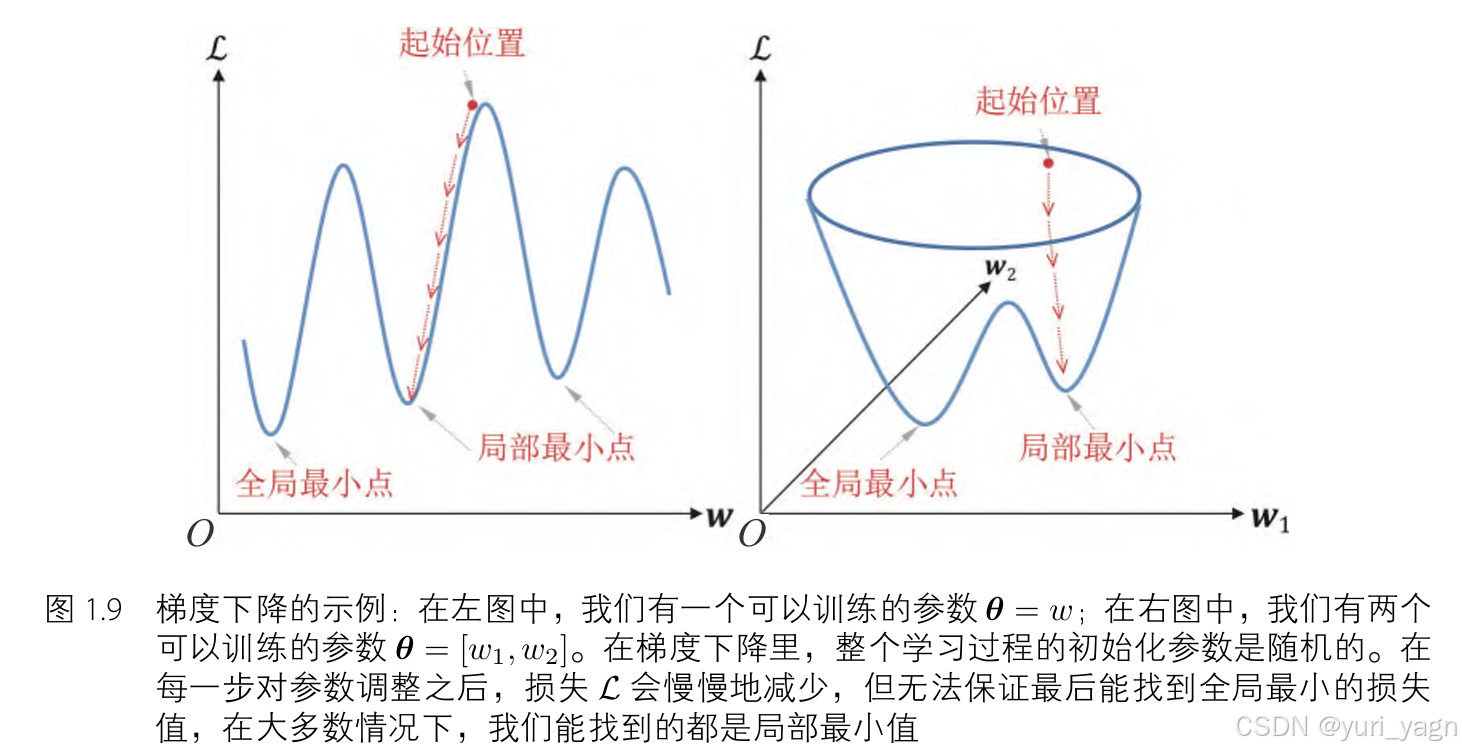
文章目录 损失函数交叉熵损失多类别分类任务概述真实标签的独热编码交叉熵损失函数 L p 范式 \mathcal{L}_{p}\text{ 范式} Lp 范式均方误差平均绝对误差 优化梯度下降和误差的反向传播 简介 本文介绍了神经网络中的损失函数及其优化方法。损失函数用于衡量模型预测值与真实值…...

Spring Boot项目的404是如何发生的
问题 在日常开发中,假如我们访问一个Sping容器中并不存在的路径,通常会返回404的报错,具体原因是什么呢? 结论 错误的访问会调用两次DispatcherServlet:第一次调用无法找到对应路径时,会给Response设置一个…...

<数据集>手势识别数据集<目标检测>
数据集格式:VOCYOLO格式 图片数量:2400张 标注数量(xml文件个数):2400 标注数量(txt文件个数):2400 标注类别数:5 标注类别名称:[fist, no_gesture, like, ok, palm] 序号类别名称图片数框数1fist597…...

【Vue3】选项式 API
【Vue3】选项式 API 背景简介开发环境开发步骤及源码总结 背景 随着年龄的增长,很多曾经烂熟于心的技术原理已被岁月摩擦得愈发模糊起来,技术出身的人总是很难放下一些执念,遂将这些知识整理成文,以纪念曾经努力学习奋斗的日子。…...

2、如何发行自己的数字代币(truffle智能合约项目实战)
2、如何发行自己的数字代币(truffle智能合约项目实战) 1-Atom IDE插件安装2-truffle tutorialtoken3-tutorialtoken源码框架分析4-安装openzeppelin代币框架(代币发布成功) 1-Atom IDE插件安装 正式介绍基于web的智能合约开发 推…...

百日筑基第二十三天-23种设计模式-创建型总汇
百日筑基第二十三天-23种设计模式-创建型总汇 前言 设计模式可以说是对于七大设计原则的实现。 总体来说设计模式分为三大类: 创建型模式,共五种:单例模式、简单工厂模式、抽象工厂模式、建造者模式、原型模式。结构型模式,共…...

张量的基本使用
目录 1.张量的定义 2.张量的分类 3.张量的创建 3.1 根据已有数据创建张量 3.2 根据形状创建张量 3.3 创建指定类型的张量 1.张量的定义 张量(Tensor)是机器学习的基本构建模块,是以数字方式表示数据的形式。PyTorch就是将数据封装成张量…...
什么是唯一键(Unique Key)?)
Oracle(14)什么是唯一键(Unique Key)?
唯一键(Unique Key)是数据库表中的一个或多个列,它们的值必须在整个表中唯一,但允许包含NULL值。唯一键的主要目的是确保表中每一行的数据在指定的列(或列组合)中是唯一的,以防止重复数据的出现…...

PostgreSQL的引号、数据类型转换和数据类型
一、单引号和双引号(重要): 1、在mysql没啥区别 2、在pgsql中,实际字符串用单引号,双引号相当于mysql的,用来包含关键字; -- 单引号,表示user_name的字符串实际值 insert into t_user(user_nam…...
)
Mad MAD Sum-Codeforces Round 960 (Div. 2)
题目在这里 大意: MAD函数返回出现次数 ≥ 2 \geq2 ≥2的最大整数 b i b_i bi M A D ( a [ 1 , 2 , . . . i ] ) MAD(a[1,2,...i]) MAD(a[1,2,...i]) 每次操作把 a i a_i ai进行上述操作,直到全变为0为止,对每次操作的数组进行求和,记…...

Flutter 插件之 package_info_plus
当使用Flutter开发应用时,通常需要获取应用程序的基本信息,例如包名、版本号和构建号。Flutter提供了一个名为 package_info_plus 的插件,它能方便地帮助我们获取这些信息。 1. 添加依赖 首先,需要在项目的 pubspec.yaml 文件中添加 package_info_plus 的依赖。打开 pubs…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

