机器学习自学笔记——聚类
聚类的基本概念
聚类,顾名思义,就是将一个数据集中各个样本点聚集成不同的“类”。每个类中的样本点都有某些相似的特征。比如图书馆中,会把成百上千的书分成不同的类别:科普书、漫画书、科幻书等等,方便人们查找。每一种类别的书都有相似之处:比如科普书类别中的书基本上都是普及一些科学知识,这就是他们的相似之处。而聚类可以理解为“将一堆图书分为不同的类别的过程”。
这里不得不说明一下“聚类”和“分类”的区别:
- 聚类是刚创立一个图书馆,通过各种渠道获得了一堆图书,事先我不知道可以分为哪些类,但是随着分类的进行,逐渐被分为不同的类。这是一种无监督学习。
- 分类是现在有一堆图书,要将其按类别放入图书馆的书架上,这些类别都是事先确定的,比如科普类、文学类、历史类等等,按类别放入即可。这是一种监督学习。
数据的聚类方法有很多,如下图:
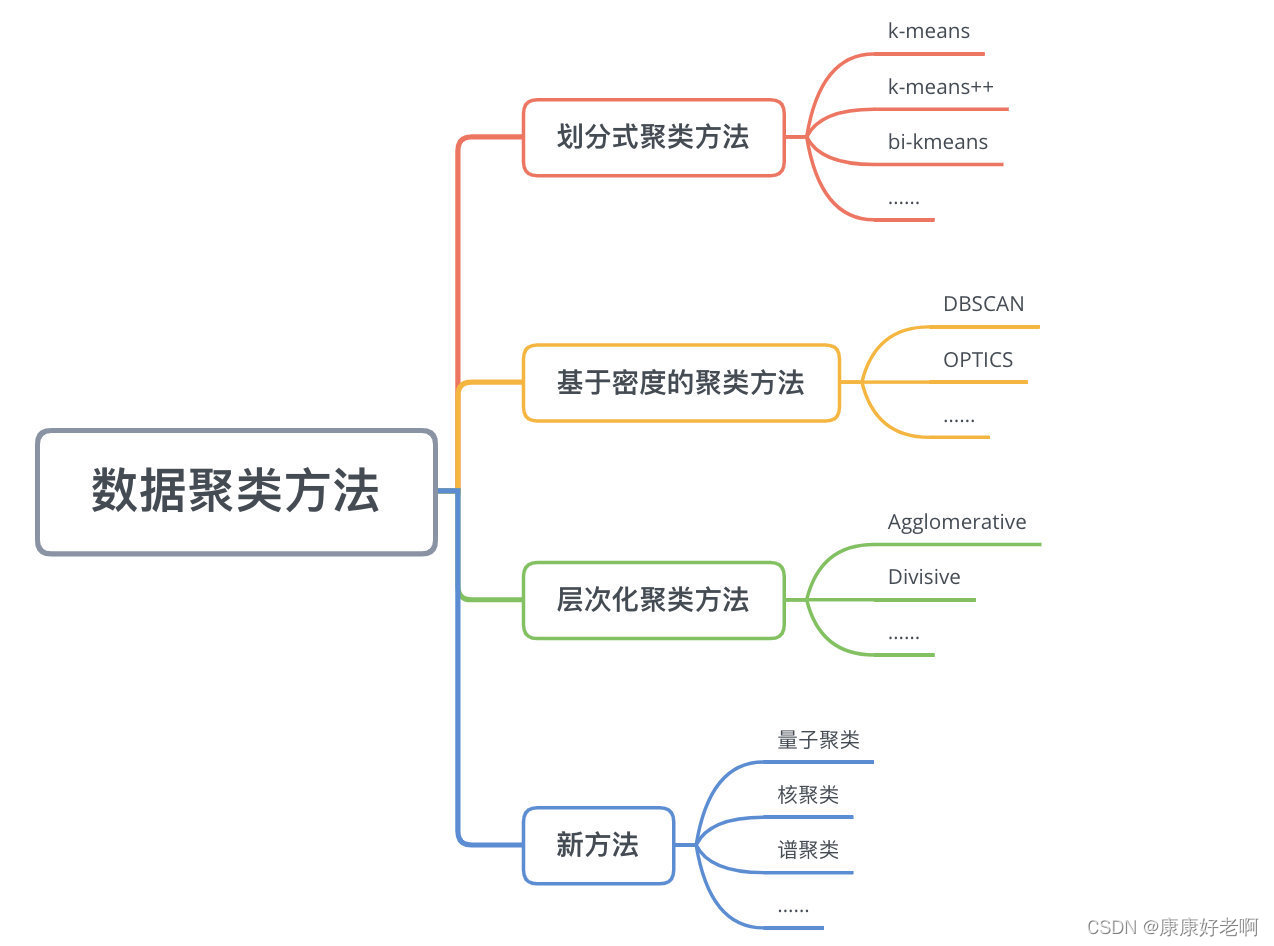
本文之后会主要介绍k-means(k均值聚类)和层次聚类算法中的聚合聚类。
上面这些聚类算法有一些共同步骤:
- 数据准备:对数据进行特征标准化和降维处理。就像将事先准备好的一本本图书一本本堆叠规整放好
- 特征选择/提取:从最初的特征中选择最有效的特征,进行转换形成新的突出特征,并将其存储在向量中。就像将图书中十分破烂或者不良的剔除,并存储在专门存储图书的地方
- 进行聚类:基于某种距离函数进行相似度度量,并形成聚簇。就像按照某种规律(书名出现相同的字)将图书之间归类(都出现百科归一类、都出现秋天归一类······)
- 结果评估:对聚类的分类结果进行评估,判断聚类进行的优劣。就像将图书聚类完之后,抽取图书并翻看内容来判断其类别是否正确
相似度度量
在上面的聚类算法的步骤中,“进行聚类”这一步骤中出现了“相似度度量”,这也是聚类算法中最重要的点。比如像我用图书的例子进行类比时,在“进行聚类”这一步说得就十分不清楚,因为我没法找到一个合适的标准去衡量图书之间的相似程度。
在聚类算法中,我们会通过计算“距离”去衡量相似度。当我们将特征数字化之后,特征之间是否相似也就是特征数字之间是否大小接近。需要注意的是,这里的“距离”是广义距离,并不仅仅是我们通常理解的d1−d2d_1-d_2d1−d2这种距离。下面我们来看几种比较常见的距离:
1、闵可夫斯基距离
① 欧式距离
欧式距离就是我们最常见的距离度量方法,就是两点之间的最短距离。
假设两个点的坐标分别为x1(x11,x12,x13,⋅⋅⋅,x1n)x_1(x_{11},x_{12},x_{13},···,x_{1n})x1(x11,x12,x13,⋅⋅⋅,x1n),x2(x21,x22,x23,⋅⋅⋅,x2n)x_2(x_{21},x_{22},x_{23},···,x_{2n})x2(x21,x22,x23,⋅⋅⋅,x2n),(我们也称x11,x12,x13,⋅⋅⋅,x1nx_{11},x_{12},x_{13},···,x_{1n}x11,x12,x13,⋅⋅⋅,x1n为x1x_1x1的特征)则这两个点的欧式距离为:
L(x1,x2)=∑i=1n(x1i−x2i)2L(x_1,x_2)=\sqrt{\sum_{i=1}^n{(x_{1i}-x_{2i})^2}} L(x1,x2)=i=1∑n(x1i−x2i)2
② 曼哈顿距离
假设两个点的坐标分别为x1(x11,x12,x13,⋅⋅⋅,x1n)x_1(x_{11},x_{12},x_{13},···,x_{1n})x1(x11,x12,x13,⋅⋅⋅,x1n),x2(x21,x22,x23,⋅⋅⋅,x2n)x_2(x_{21},x_{22},x_{23},···,x_{2n})x2(x21,x22,x23,⋅⋅⋅,x2n),则这两个点的曼哈顿距离为:
L(x1,x2)=∑i=1n∣x1i−x2i∣L(x_1,x_2)=\sum_{i=1}^n|x_{1i}-x_{2i}| L(x1,x2)=i=1∑n∣x1i−x2i∣
③ 切比雪夫距离
假设两个点的坐标分别为x1(x11,x12,x13,⋅⋅⋅,x1n)x_1(x_{11},x_{12},x_{13},···,x_{1n})x1(x11,x12,x13,⋅⋅⋅,x1n),x2(x21,x22,x23,⋅⋅⋅,x2n)x_2(x_{21},x_{22},x_{23},···,x_{2n})x2(x21,x22,x23,⋅⋅⋅,x2n),则这两个点的切比雪夫距离为:
L(x1,x2)=(∑i=1n∣x1i−x2i∣p)1pL(x_1,x_2)=(\sum_{i=1}^n|x_{1i}-x_{2i}|^p)^{\frac{1}{p}} L(x1,x2)=(i=1∑n∣x1i−x2i∣p)p1
其中p趋于正无穷。
其实,上面三种计算方法可以进行一个统一,这就是这一部分的小标题——闵可夫斯基距离。欧氏距离是闵可夫斯基距离L(x1,x2)=(∑i=1n∣x1i−x2i∣p)1pL(x_1,x_2)=(\sum_{i=1}^n|x_{1i}-x_{2i}|^p)^{\frac{1}{p}}L(x1,x2)=(∑i=1n∣x1i−x2i∣p)p1中p=2p=2p=2的结果,曼哈顿距离是该式p=1p=1p=1的结果,而切比雪夫距离是p=+∞p=+\infinp=+∞的结果
2、马氏距离
马氏距离全称马哈拉诺比斯距离。样本不同的特征之间大小尺寸可能会不同,比如特征1两个数据为10000和20000,特征2两个数据为1和2。如果只考虑其距离,那么10000与12000之间相差的数字肯定要比1与2之间相差的数字要大,但这并不意味着前者的相似度一定要比后者更小,因为他们的尺寸不同难以比较,所以使用马氏距离可以避免这种问题:
dij=[(xi−xj)TS−1(xi−xj)]12d_{ij}=[(x_i-x_j)^TS^{-1}(x_i-x_j)]^\frac{1}{2} dij=[(xi−xj)TS−1(xi−xj)]21
其中xix_ixi是样本iii的特征矩阵,xjx_jxj是样本jjj的特征矩阵,SSS是样本集合XXX的协方差矩阵。
3、相关系数
相关系数的定义表达式为:
rij=∑k=1m(xki−x‾i)(xkj−x‾j)[∑k=1m(xki−x‾i)2∑k=1m(xkj−x‾j)2]12r_{ij}=\frac{\sum_{k=1}^{m}(x_{ki}-\overline x_i)(x_{kj}-\overline x_j)}{[\sum_{k=1}^{m}(x_{ki}-\overline x_i)^2\sum_{k=1}^{m}(x_{kj}-\overline x_j)^2]^\frac12} rij=[∑k=1m(xki−xi)2∑k=1m(xkj−xj)2]21∑k=1m(xki−xi)(xkj−xj)
相关系数越接近1,表示样本越相似;相关系数越接近0,表示样本越不相似。
4、夹角余弦
夹角余弦的定义表达式为:
sij=∑k=1mxkixkj[∑k=1mxki2∑k=1mxkj2]12s_{ij}=\frac{\sum_{k=1}^{m}x_{ki}x_{kj}}{[\sum_{k=1}^{m}x_{ki}^2\sum_{k=1}^{m}x_{kj}^2]^\frac12} sij=[∑k=1mxki2∑k=1mxkj2]21∑k=1mxkixkj
夹角余弦越接近1,表示样本越相似;夹角余弦越接近0,表示样本越不相似。
上面的这些距离是样本点之间的距离,在聚类算法中,我们还需要一种衡量类与类之间的距离方法,常见的有以下四种:
(1)最短距离/单链接(Single-link):
定义两个类的样本之间的最短距离为两类之间的距离。
缺点:容易出现包含范围特别大的类,因为并没有对两个类的最大距离进行限制。
(2)最长距离/完全链接(Complete-link):
定义两个类的样本之间的最长距离为两类之间的距离。
缺点:容易受到异常样本点的影响而造成不合理的聚类,因为异常样本点很容易干扰最长距离。
(3)中心距离(UPGMA):
定义两个类的样本中心之间的距离为两类之间的距离。
(4)平均距离(WPGMA):
定义两个类任意样本之间的距离的平均为两类之间的距离。
聚合聚类
聚合聚类是一种层次聚类算法,主要分为两种:聚合聚类和分类聚类。聚合聚类开始将每个样本各自分到一个类之中,之后再讲相距最近的两个类合并,最终生成一个类;而分裂聚类正好相反,先将所有样本分到一个类之中,再将样本中距离最远的分到两个新的类。这里只介绍聚合聚类。
算法步骤:
- (1)计算样本两两之间的欧式距离,构造距离矩阵
- (2)将每个样本都变成一个类:G1,G2,⋅⋅⋅,GnG_1,G_2,···,G_nG1,G2,⋅⋅⋅,Gn
- (3)定义**最短距离(Single-link)**为类间距离,找出距离最小的两个类归为一个新的类
- (4)如果只剩下一个类,那么停止运算,否则继续重复(3)(4)
算法复杂度:O(n3m)O(n^3m)O(n3m),nnn是样本个数,mmm是样本维数
K均值聚类
K均值聚类是已知要将原数据样本分成k个类,但是并不知道这k个类具体是什么。刚开始要随机选取k个点作为样本的初始中心点,这k个点各自属于一个类别。再通过比较距离大小将剩余的点分到这k个点对应的类别之中。
算法步骤:
- (1)初始化,随机选取k个点作为初始的聚类中心,这k个点各属于一个类别
- (2)计算每个样本到聚类中心的距离,并将其归类到与其距离最近的类之中
- (3)通过对每个样本取均值计算每个类新的聚类中心(因为加入了新的点),重复(2)的操作
- (4)如果两次操作所得到的分类相同,则停止操作。否则继续重复(2)(3)的操作
算法的复杂度:O(nmk)O(nmk)O(nmk),nnn是样本个数,mmm是样本维数,kkk是类别个数
相关文章:

机器学习自学笔记——聚类
聚类的基本概念 聚类,顾名思义,就是将一个数据集中各个样本点聚集成不同的“类”。每个类中的样本点都有某些相似的特征。比如图书馆中,会把成百上千的书分成不同的类别:科普书、漫画书、科幻书等等,方便人们查找。每…...
注意下C语言整形提升
C语言整形提升 C语言整形提升是指在表达式中使用多种类型的数据时,编译器会自动将较小的类型转换为较大的类型,以便进行运算。在C语言中,整型提升规则如下: 如果表达式中存在short类型,则将其自动转换为int类型。 如…...

Go panic的学习
一、前言 我们的应用程序常常会出现异常,包括由运行时检测到的异常或者应用开发者自己抛出的异常。 异常在一些其他语言中,如c、java,被叫做Exception,主要由抛出异常和捕获异常两部分组成。异常在go语言中,叫做pani…...

讲解Linux中samba理论讲解及Linux共享访问
♥️作者:小刘在C站 ♥️个人主页:小刘主页 ♥️每天分享云计算网络运维课堂笔记,努力不一定有收获,但一定会有收获加油!一起努力,共赴美好人生! ♥️夕阳下,是最美的绽放࿰…...
【C++笔试强训】第三十二天
🎇C笔试强训 博客主页:一起去看日落吗分享博主的C刷题日常,大家一起学习博主的能力有限,出现错误希望大家不吝赐教分享给大家一句我很喜欢的话:夜色难免微凉,前方必有曙光 🌞。 💦&a…...

OpenAI GPT-4震撼发布:多模态大模型
OpenAI GPT-4震撼发布:多模态大模型发布要点GPT4的新功能GPT-4:我能玩梗图GPT4:理解图片GPT4:识别与解析图片内容怎样面对GPT4申请 GPT-4 API前言: 🏠个人主页:以山河作礼。 📝📝:本文章是帮助大家更加了…...

手把手教你 在linux上安装kafka
目录 1. 准备服务器 2. 选一台服务器配置kafka安装包 2.1 下载安装包 2.2 解压安装包 2.3 修改配置文件 3. 分发安装包到其他机器 4. 修改每台机器的broker.id 5. 配置环境变量 6. 启停kafka服务 6.1 启动kafak服务 6.2 停止kafka服务 1. 准备服务器 1.买几台云服务…...

Spring Cloud(微服务)学习篇(五)
Spring Cloud(微服务)学习篇(五) 1 nacos配置文件的读取 1.1 访问localhost:8848/index.html并输入账户密码后进入nacos界面并点击配置列表 1.2 点击右侧的号 1.3 点击加号后,进入新建配置界面,并做好如下配置 1.4 往下翻动,点击发布按钮 1.5 发布成功后的界面 1.6 在pom.xml…...

道阻且长,未来可期,从GPT-4窥得通用人工智能时代的冰山一角!
大家这两天是不是又被满屏的ChatGPT相关的文章信息给轰炸得不轻,说实话,我真的对ChatGPT的热度如此经久不衰这个问题非常感兴趣。从去年刚面世时,小范围内造成的行业震荡,到今年二月份铺天盖地得铺舆论造势,引发全民热…...

百度将?百度已!
仿佛一夜之间,创业公司OpenAI旗下的ChatGPT就火遍全球。这是一场十分罕见的科技盛宴。下到普通用户,上到各科技大厂都在讨论ChatGPT的前景,国外的微软、谷歌,国内的百度、腾讯、阿里等等都在布局相关业务。比尔盖茨更是称ChatGPT与…...
内核实验(三):编写简单Linux内核模块,使用Qemu加载ko做测试
文章目录一、篇头二、QEMU:挂载虚拟分区2.1 创建 sd.ext4.img 虚拟分区2.2 启动 Qemu2.3 手动挂载 sd.ext4.img三、实现一个简单的KO3.1 目录文件3.2 Makefile3.3 编译3.3.1 编译打印3.3.2 生成文件3.4 检查:objdump3.4.1 objdump -dS test\_1.ko3.4.2 o…...
女子举重问题
一、问题的描述 问题及要求 1、搜集各个级别世界女子举重比赛的实际数据。分别建立女子举重比赛总成绩的线性模型、幂函数模型、幂函数改进模型,并最终建立总冠军评选模型。 应用以上模型对最近举行的一届奥运会女子举重比赛总成绩进行排名,并对模型及…...

试题 历届真题 循环小数【第十一届】【决赛】【Python】
试题 历届真题 循环小数【第十一届】【决赛】【Python】 题目来源:第十一届蓝桥杯决赛 http://lx.lanqiao.cn/problem.page?gpidT2891 资源限制 内存限制:256.0MB C/C时间限制:1.0s Java时间限制:3.0s Python时间限制ÿ…...

关于类型转换
隐式转换先看个例子int a {500}; unsigned b {1000}; std::cout<<a-b;这里的输出结果并不为-500。因为最后输出结果的类型自动转换成了unsigned,unsigned是正整数型类型转换顺序表(由高到低)long doubledoublefloatunsigned long long long longunsigned long…...
蓝桥杯冲击-02约数篇(必考)
文章目录 前言 一、约数是什么 二、三大模板 1、试除法求约数个数 2、求约数个数 3、求约数之和 三、真题演练 前言 约数和质数一样在蓝桥杯考试中是在数论中考察频率较高的一种,在省赛考察的时候往往就是模板题,难度大一点会结合其他知识点考察&#x…...

122.(leaflet篇)leaflet地图图片之间存在缝隙
听老人家说:多看美女会长寿 地图之家总目录(订阅之前建议先查看该博客) 文章末尾处提供保证可运行完整代码包,运行如有问题,可“私信”博主。 存在缝隙–效果如下所示: 解决缝隙–效果如下所示: 下面献上完整代码,代码重要位置会做相应解释 <!DOCTYPE html>…...
4.类的基本概念
目录 4.1 类的概述 类是一种活动的数据结构 4.2 程序和类:一个快速实例 4.3 声明类 4.4 类成员 4.4.1 字段 1.显示和隐式字段初始化 2. 声明多个字段 4.4.2 方法 4.5 创建变量和类的实例 4.6 为数据分配内存 合并这两个步骤 4.7 实例成员 4.8 访问修饰…...
有图解有案例,我终于把 Condition 的原理讲透彻了
哈喽大家好,我是阿Q! 20张图图解ReentrantLock加锁解锁原理文章一发,便引发了大家激烈的讨论,更有小伙伴前来弹窗:平时加解锁都是直接使用Synchronized关键字来实现的,简单好用,为啥还要引用Re…...
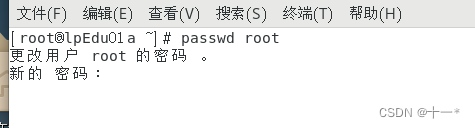
Linux之找回root密码
文章目录前言一、启动系统二、进入编辑界面三、修改密码前言 当我们使用root用户登陆Linux时,忘记了登陆密码,改怎样修改登陆密码呢,接下来将介绍如何修改root密码 一、启动系统 首先,启动系统,进入开机界面&#x…...
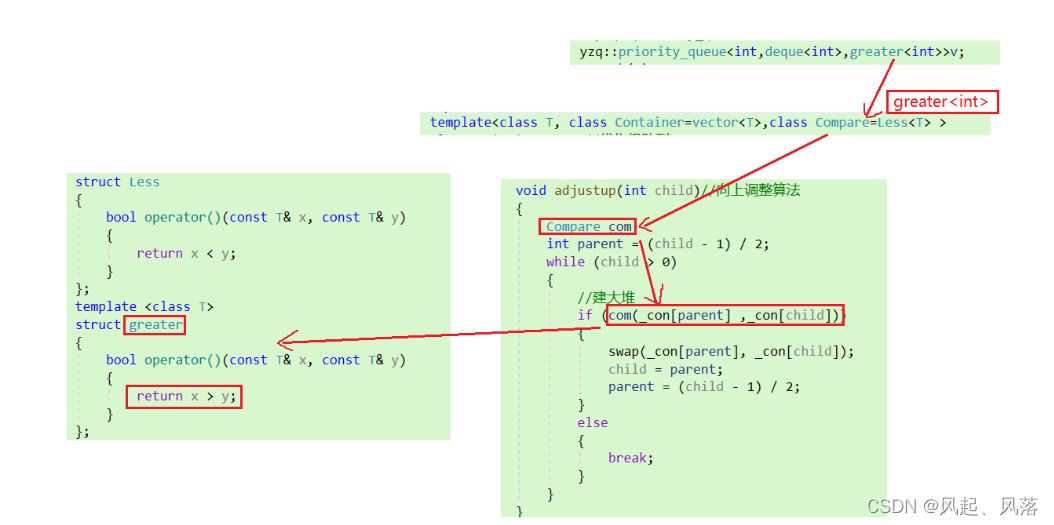
stack_queue | priority_queue | 仿函数
文章目录1. stack 的使用2. stack的模拟实现3. queue的使用4. queue的模拟实现5. deque ——双端队列deque优缺点6. priority_queue ——优先级队列1. priority_queue的使用2. priority_queue的模拟实现push——插入pop ——删除top —— 堆顶仿函数问题完整代码实现1. stack 的…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...
