女子举重问题
一、问题的描述
问题及要求
1、搜集各个级别世界女子举重比赛的实际数据。分别建立女子举重比赛总成绩的线性模型、幂函数模型、幂函数改进模型,并最终建立总冠军评选模型。
应用以上模型对最近举行的一届奥运会女子举重比赛总成绩进行排名,并对模型及结果进行必要的分析。
2、请对以上模型作进一步的改进,或提出更好的模型,并应用模型进行排名。
3、同样对最近举行的一届奥运会所有男女举重冠军行进评选,选出1名最优秀的举重运动员,给出你的定量评选方法并合理论述。
4、由以上研究过程及结果结论的启发,你认为这个模型可以推广应用到生活或学习中的哪些情况下,或者应该对生活或学习中哪些事物现有的处理方式需要做出改进,请给出你的分析。
说明:完成一篇建模论文。(具体资料及提交要求见说明文件)
二、搜集资料和数据
1.级别的划分
以下括号内容均为网上的查阅资料
(男子举重原有8个级别是:56、62、69、77、85、94、105公斤级和105公斤以上级,于2018年由国际举联调整新的10个级别是55(非奥)、61、67、73、81、89(非奥)、96、102(非奥)、109公斤级和109公斤以上级共10个级别。女子举重原来7个级别是:48、53、58、63、69、75公斤级和75公斤级以上级,新的10个级别也调整为:45(非奥)、49、55、59、64、71(非奥)、76、81(非奥)、87公斤级和87公斤以上级。男女6个非奥级别只在奥运会以外的赛事举行。)
在本题目中,我们按照奥运会的规定来进行求解,规定为8个级别(在下面做的时候用的是10个级别)
男运动员:61、67、73、81、96、109、109以上
女运动员:49、55、59、64、76、87、87以上
2.搜集数据
数据来源:
女子举重世界纪录_国家体育总局 (sport.gov.cn)(旧纪录不可用,这是一个注意点,一定要注意,要用2018以后的数据,新标准之下的记录)
图1.旧标准的记录
可用数据网站(需要科学上网):https://zh.wikipedia.org/zh-hans/%E8%88%89%E9%87%8D%E4%B8%96%E7%95%8C%E7%B4%80%E9%8C%84%E5%88%97%E8%A1%A8#%E5%A5%B3%E5%AD%90
在这个网站里面,我们需要选取,当前记录这一栏目,千万千万千万记住,不要用旧纪录这一栏,因为在2018年之后男子和女子的分类的级别已经改变。
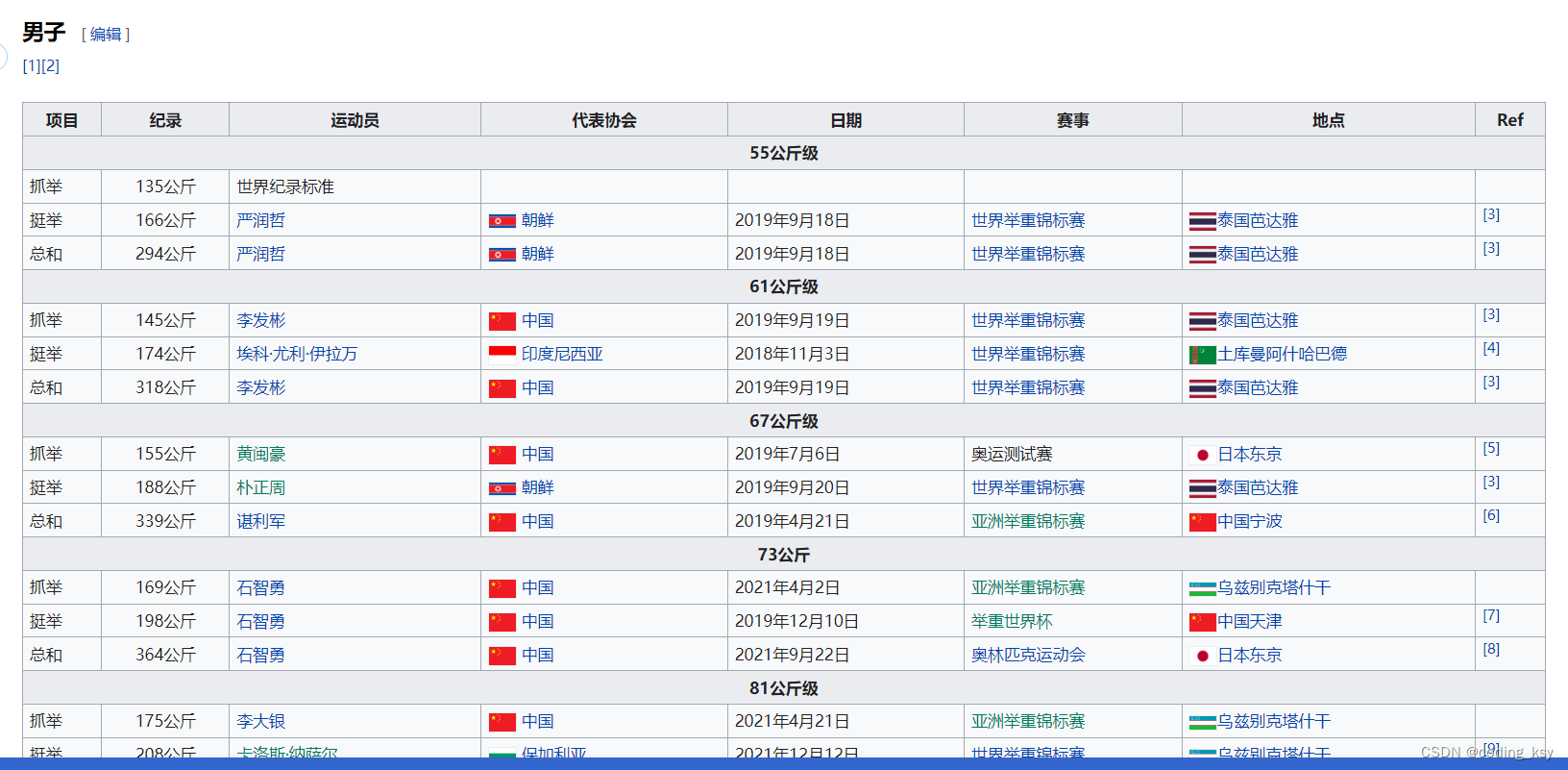
图2.男子新记录
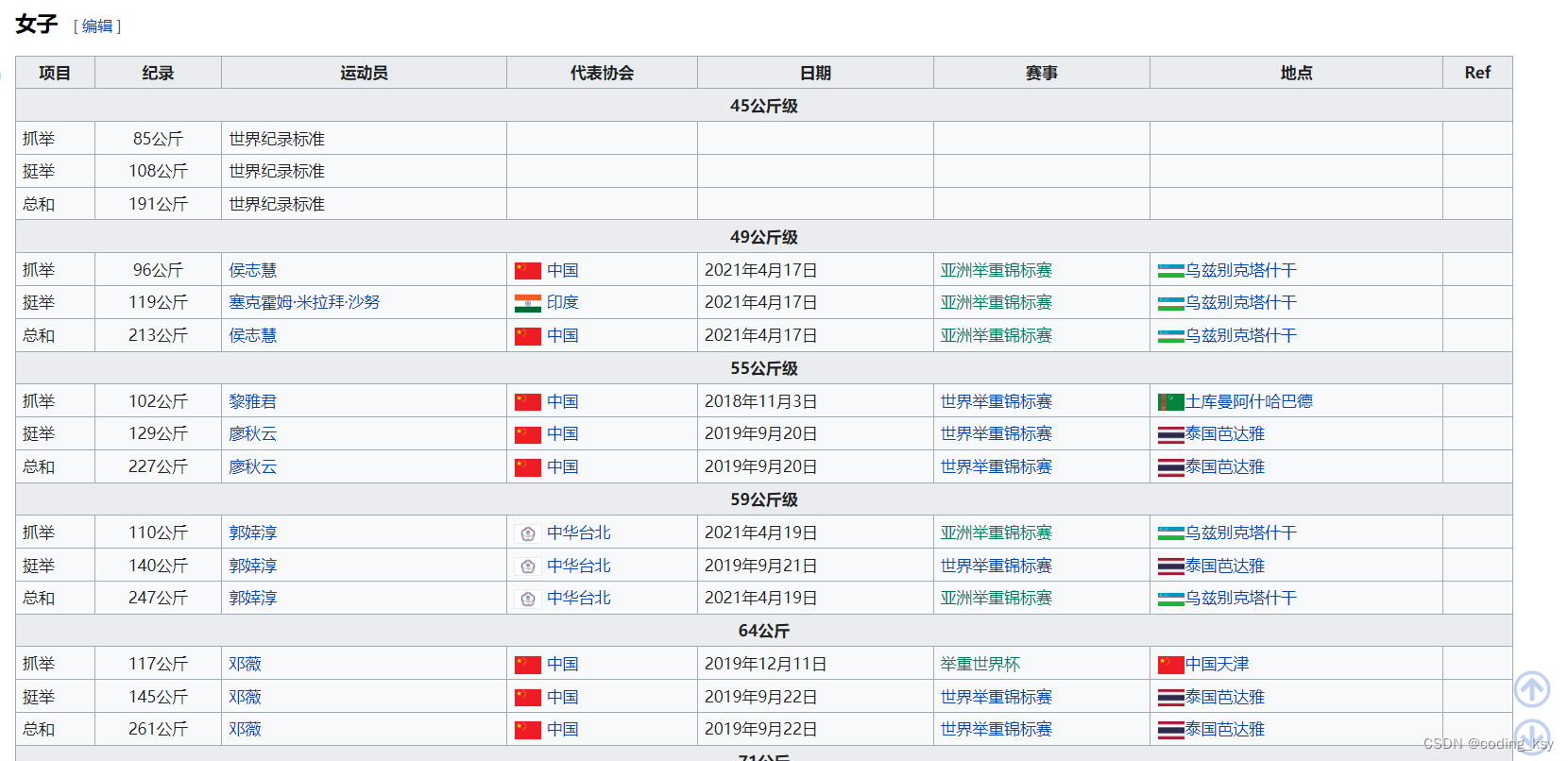
图3.女子新纪录
三、第一问
1.分别绘制抓举、挺举、总和下的散点图如下:
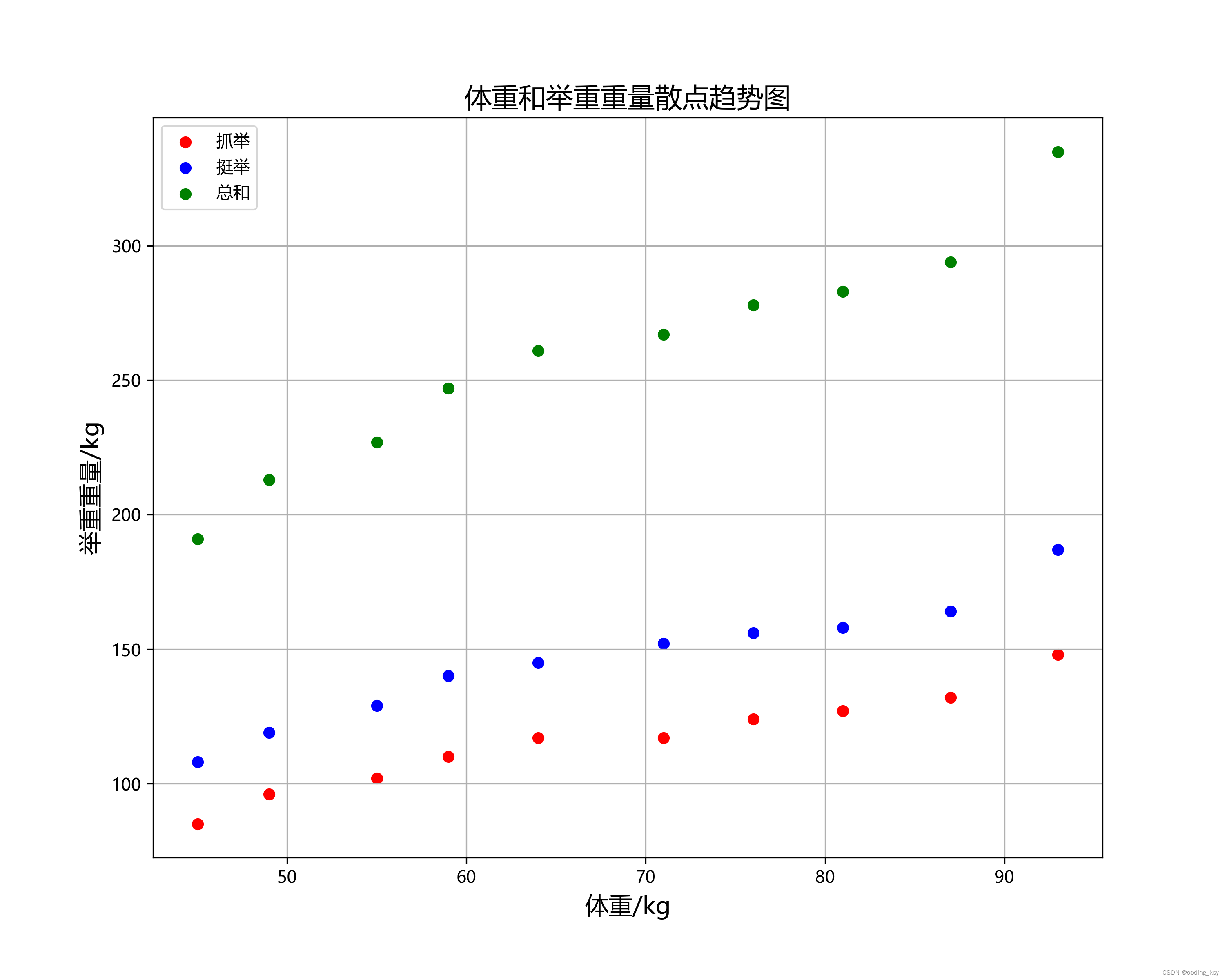
图4.体重和举重重量的散点趋势图
分析图形可能为线性关系、非线性关系(指数、对数等)。
散点图代码如下(python):
#引入相应的库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns#读取数据
data=pd.read_excel("data.xlsx",sheet_name="女子")
#选取抓举、挺举、总和
data_1=data[data["class"]=="抓举"].sort_values("weight")
data_2=data[data["class"]=="挺举"].sort_values("weight")
data_3=data[data["class"]=="总和"].sort_values("weight")
#筛选出自变量和因变量
x1=data_1["weight"].values
y1=data_1["record"].values
x2=data_2["weight"].values
y2=data_2["record"].values
x3=data_3["weight"].values
y3=data_3["record"].values#解决中文乱码和符号显示的问题
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['font.sans-serif']=['Microsoft YaHei']
#绘制散点图
plt.figure(figsize=(10,8),dpi=300)
plt.title("体重和举重重量散点趋势图",fontsize="16")
plt.xlabel("体重/kg",fontsize="14")
plt.ylabel("举重重量/kg",fontsize="14")
plt.scatter(x1,y1,color="red",label="抓举")
plt.scatter(x2,y2,color="blue",label="挺举")
plt.scatter(x3,y3,color="green",label="总和")
plt.grid(True)
plt.legend()
plt.savefig("1.png")2.线性拟合
拟合图如下
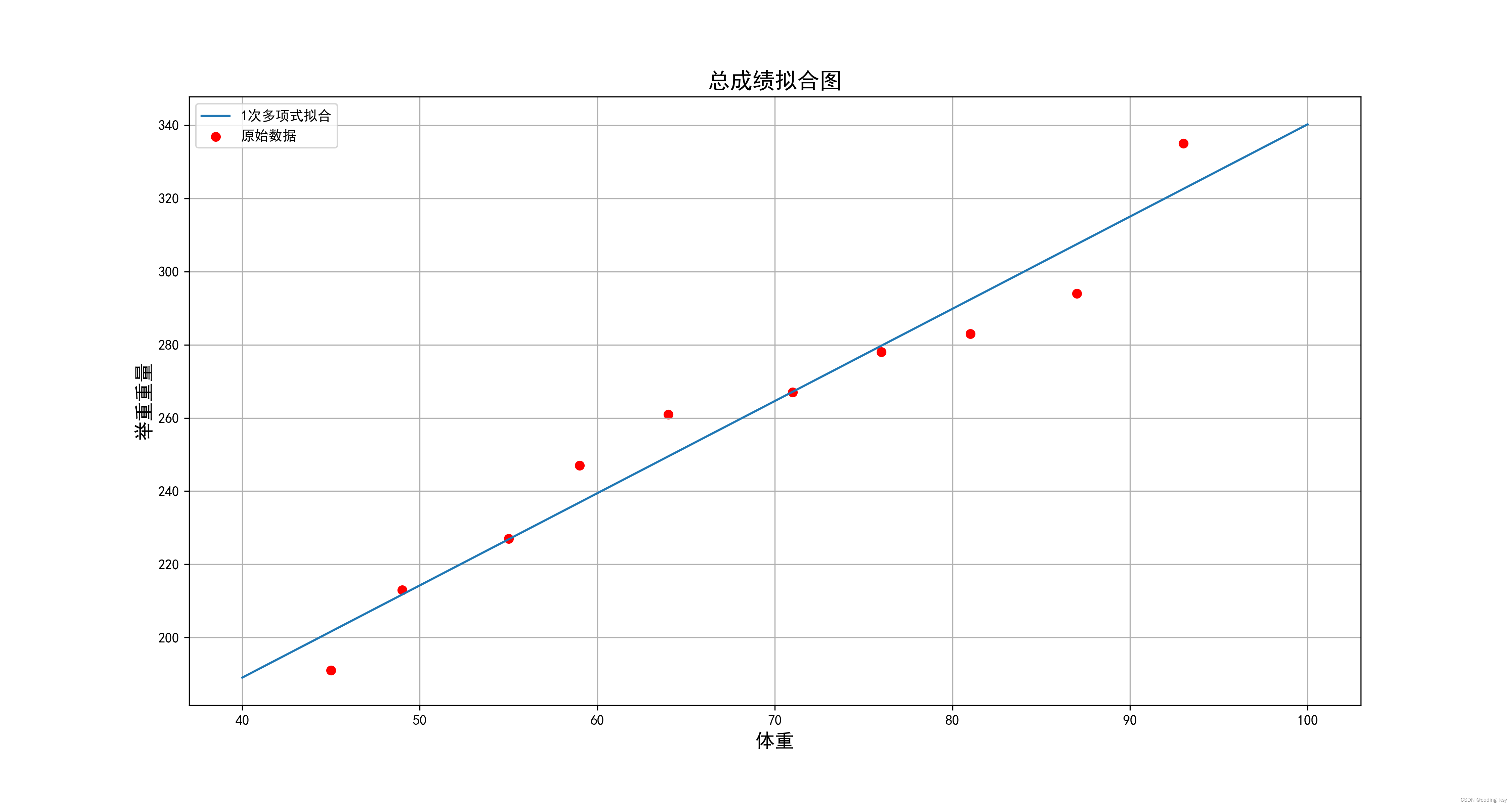
计算结果

从上面的结果中我们可以看出,当多项式的最高次数大于4次的时后,虽然模型的R的平方较好,但是不符合实际情况,属于过拟合现象,上面的参数RMSE和MAE来计算误差的话,无法排除离群点的影响,所以采用了MAPE来计算误差的话,这样就排除离群点对模型的影响。这个多项式拟合可以用到第二问当中去,作为模型的改进。
2.幂函数拟合
相关的理论支持:
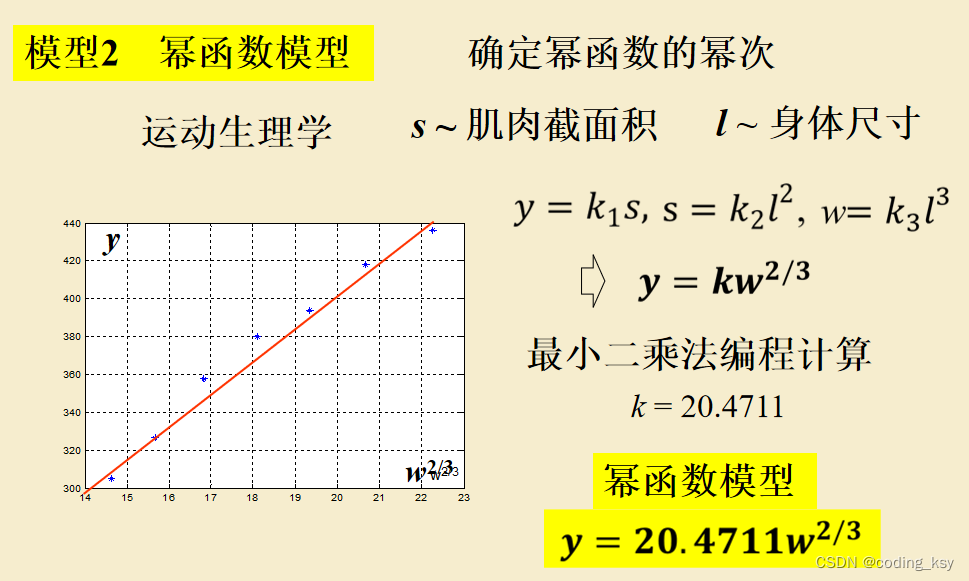
上图中的参数是举例子
拟合效果图如下:
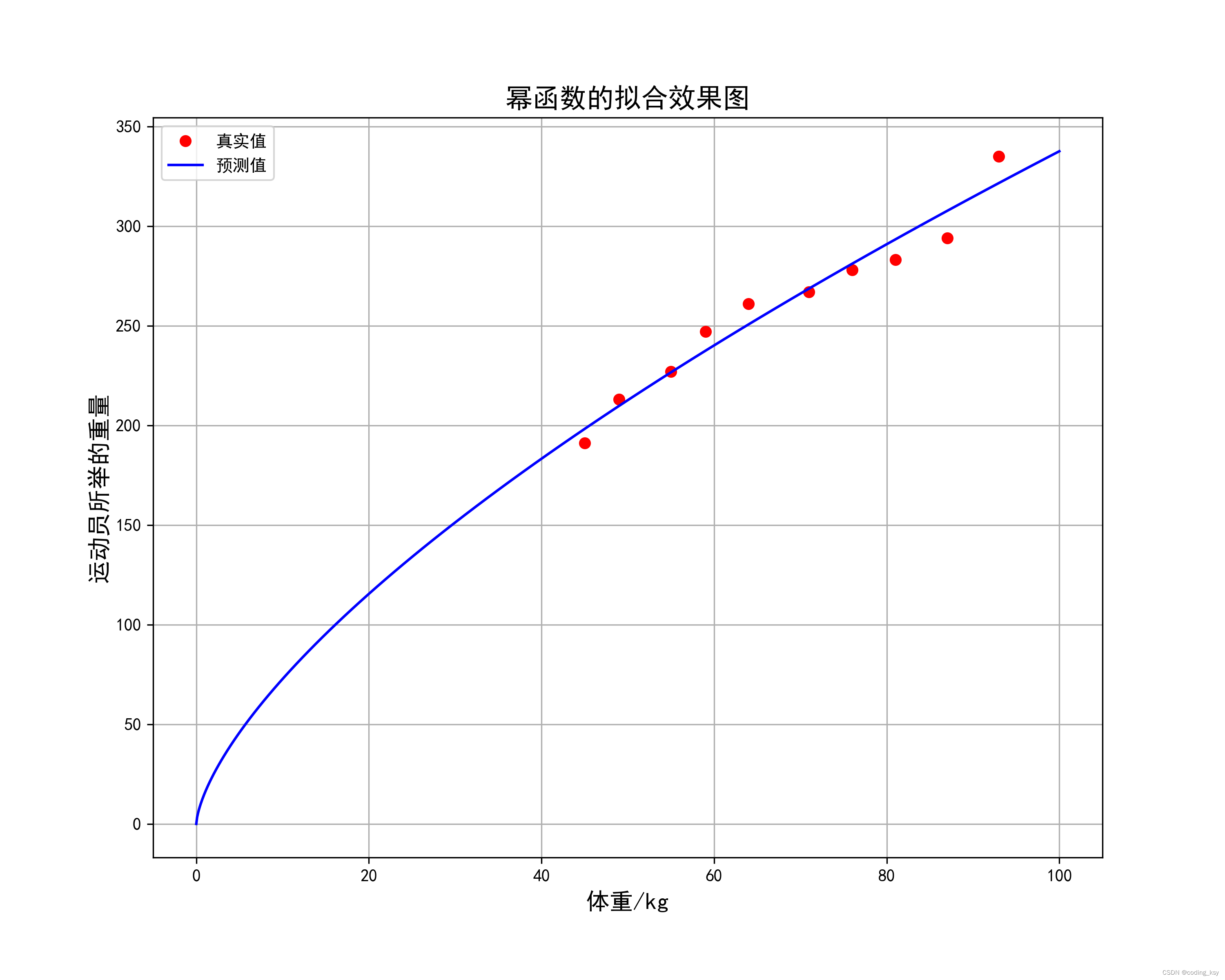
模型的评估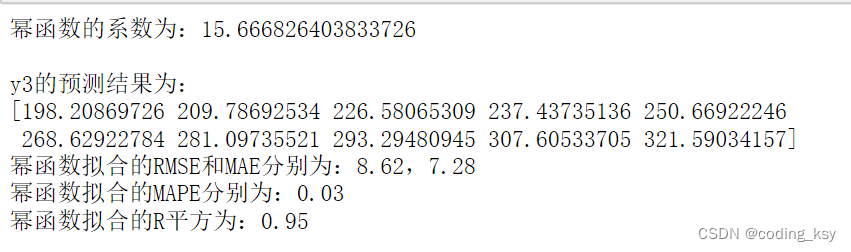
上面的参数RMSE和MAE来计算误差的话,无法排除离群点的影响,所以采用了MAPE来计算误差的话,这样就排除离群点对模型的影响。
#幂函数进行拟合#引入相应的库
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit# 自定义的拟合函数
def func2(x,k):return k*np.power(x,2/3)# 开始拟合
popt, pcov = curve_fit(func2, x3, y3)# 提取拟合结果
k = popt[0]#幂函数的系数
print("幂函数的系数为:{:}\n".format(k))
print("y3的预测结果为:")
y_predict=func2(x3,k)#预测的结果值
print(y_predict)x_new = np.linspace(0, 100, 1000) # 生成新的x轴数据
#绘制拟合曲线效果
plt.figure(figsize=(10,8),dpi=300)
plt.title("幂函数的拟合效果图",fontsize=16)
plt.xlabel("体重/kg",fontsize=14)
plt.ylabel("运动员所举的重量",fontsize=14)
plt.plot(x3,y3,"ro",label="真实值")
plt.plot(x_new,func2(x_new,k),color='blue',label="预测值")
plt.grid(True)
plt.legend(loc="upper left")
plt.savefig("3.png")#误差分析
rmse_poly = np.sqrt(np.mean((y3 - func2(x3,k))**2))
mae_poly = np.mean(np.abs(y3 - func2(x3,k)))
mape_poly=np.mean(np.abs(y3-func2(x3,k))/func2(x3,k))# 打印RMSE和MAE
print("幂函数拟合的RMSE和MAE分别为:{:.2f},{:.2f}".format(rmse_poly, mae_poly))
print("幂函数拟合的MAPE分别为:{:.2f}".format(mape_poly))
y_poly = poly(x_new)
# 计算R平方
r2_poly = r2_score(y3, func2(x3,k))
# 打印R平方
print("幂函数拟合的R平方为:{:.2f}".format(r2_poly))
print("\n")3.改进幂函数的拟合
相关的理论支持:

上图中的参数是举例子
改进幂函数的拟合效果图
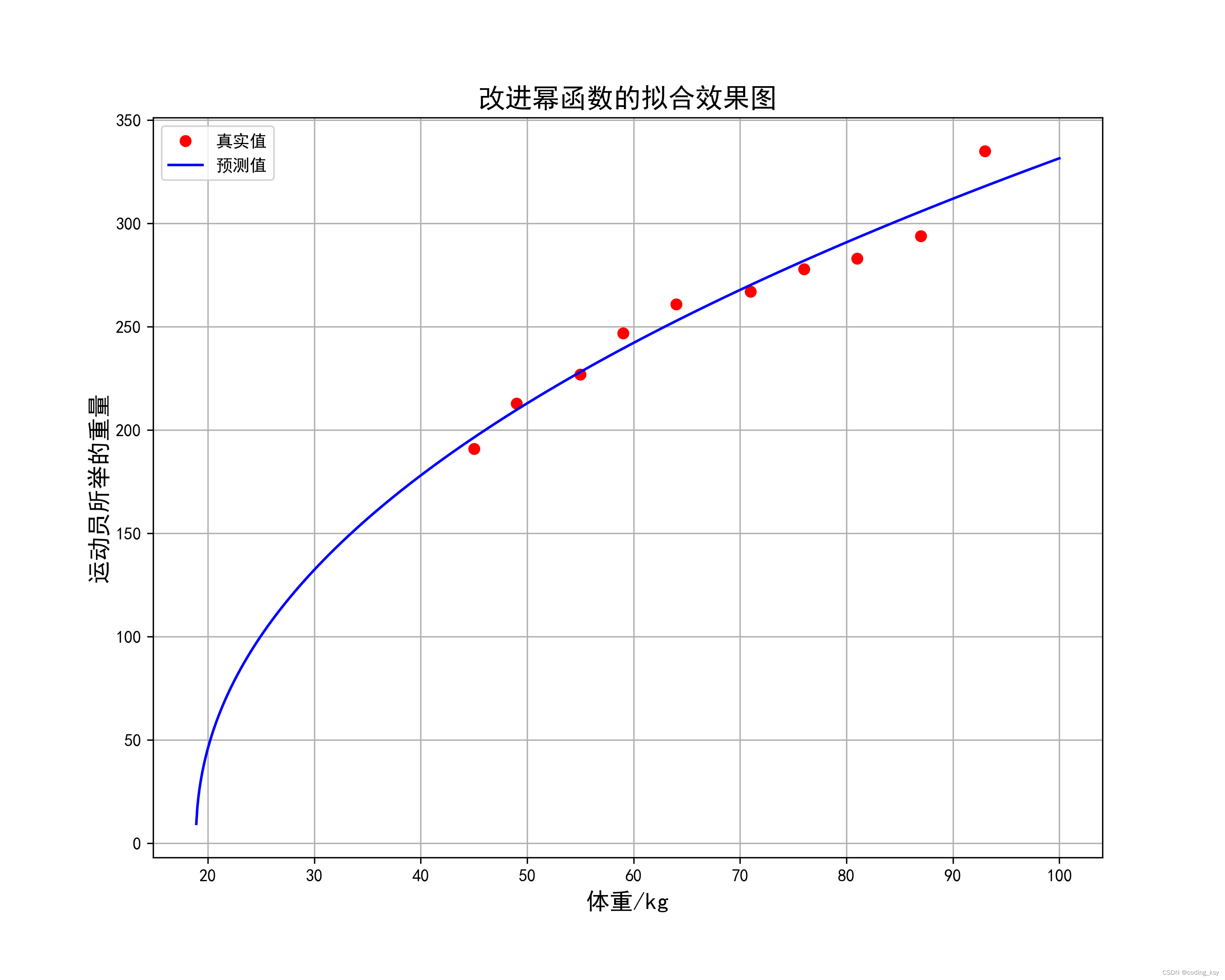
误差分析:

上面的参数RMSE和MAE来计算误差的话,无法排除离群点的影响,所以采用了MAPE来计算误差的话,这样就排除离群点对模型的影响。
#改进幂函数
#幂函数进行拟合#引入相应的库
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit# 自定义的拟合函数
def func2(x,k,w0,l):return k*np.power(x-w0,l)# 开始拟合
popt, pcov = curve_fit(func2, x3, y3)# 提取拟合结果
k = popt[0]#改进幂函数的系数k
w0=popt[1]#改进幂函数的w0
l=popt[2]#改进幂函数的l
print("改进幂函数的系数为:{:}\n".format(k))
print("改进幂函数的w0为:{:}\n".format(w0))
print("改进幂函数的l为:{:}\n".format(l))
print("y3的预测结果为:")
y_predict=func2(x3,k,w0,l)#预测的结果值
print(y_predict)x_new = np.linspace(0, 100, 1000) # 生成新的x轴数据
#绘制拟合曲线效果
plt.figure(figsize=(10,8),dpi=300)
plt.title("改进幂函数的拟合效果图",fontsize=16)
plt.xlabel("体重/kg",fontsize=14)
plt.ylabel("运动员所举的重量",fontsize=14)
plt.plot(x3,y3,"ro",label="真实值")
plt.plot(x_new,func2(x_new,k,w0,l),color='blue',label="预测值")
plt.grid(True)
plt.legend(loc="upper left")
plt.savefig("4.png")#误差分析
rmse_poly = np.sqrt(np.mean((y3 - func2(x3,k,w0,l))**2))
mae_poly = np.mean(np.abs(y3 - func2(x3,k,w0,l)))
mape_poly=np.mean(np.abs(y3-func2(x3,k,w0,l))/func2(x3,k,w0,l))# 打印RMSE和MAE
print("改进幂函数拟合的RMSE和MAE分别为:{:.2f},{:.2f}".format(rmse_poly, mae_poly))
print("改进幂函数拟合的MAPE分别为:{:.2f}".format(mape_poly))
y_poly = poly(x_new)
# 计算R平方
r2_poly = r2_score(y3, func2(x3,k,w0,l))
# 打印R平方
print("改进幂函数拟合的R平方为:{:.2f}".format(r2_poly))
print("\n")综上所述,线性模型(一次)、幂函数模型、改进幂函数模型的效果大致相同,因此可以选择其中一个模型来进行下面的操作,为保持与二题的连贯性,建议选择线性模型,其次是改进幂函数模型,最后为幂函数模型。
4.标准统一化
相关理论基础:


本文选取中间级别71公斤的作为标准,使所以级别的数据转换到71公斤的标准下。
下面是总和成绩记录的所有数据
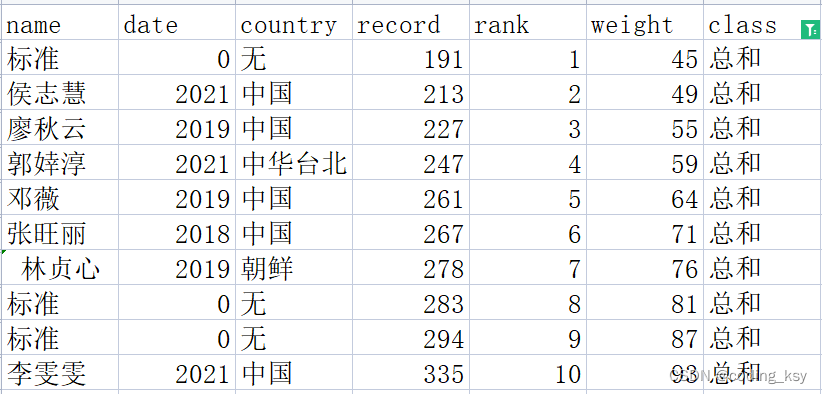
选用线性模型(一次),当然也可以选择其它模型(改进幂函数等)

即:y=2.52x+88.26
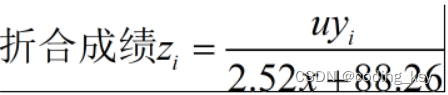
将级别6的数据代入,即可算出u=267.18
本文选取东京奥运会的举重数据进行计算,数据网站如下:
百度百科-验证
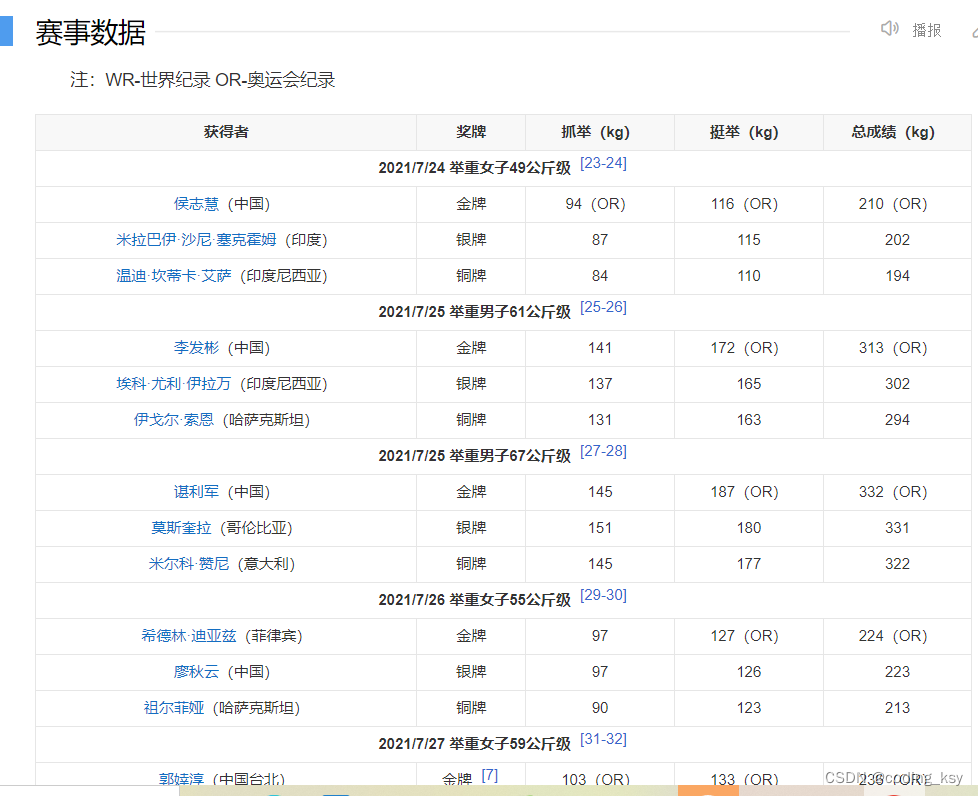
数据处理:在当年东京奥运会有的级别中选取总冠军,以该级别的最高边界值作为选手的体重。
下表为东京奥运会上各个级别的女子总冠军。
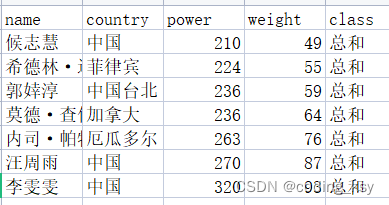
计算得出得结果如下:

可视化得分结果如下:
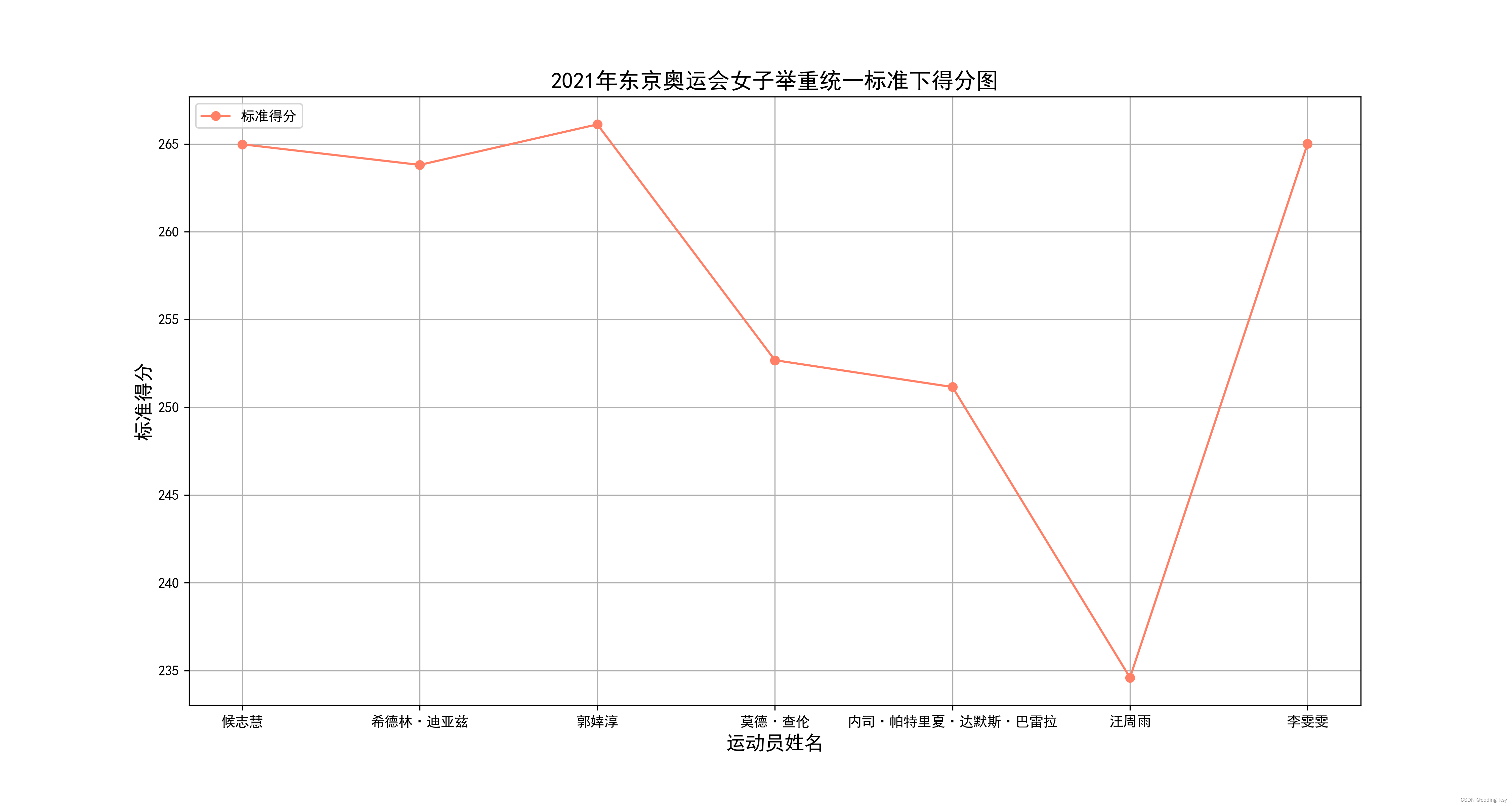
从上图可知:中国台北的郭婞淳为总冠军
代码:
#导库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
#读取数据
data=pd.read_excel("data.xlsx",sheet_name="东京奥运会女子举重")
x4=data["weight"].values
y4=data["power"].values
#定义标准化函数
coefficients = np.polyfit(x3, y3, 1) # 用1次多项式进行拟合
poly = np.poly1d(coefficients) # 生成多项式函数
def zfunc(x,y):return 267.18*y/(2.52*x+88.26)#求解运动员标准得分,该分数越大,证明运动员成绩越好
z=zfunc(x4,y4)
#将数据读入到data中
data["标准化得分"]=z#画图
x5=data["name"].values
y5=z
plt.figure(figsize=(15,8),dpi=300)
plt.title("2021年东京奥运会女子举重统一标准下得分图",fontsize=16)
plt.xlabel("运动员姓名",fontsize=14)
plt.ylabel("标准得分",fontsize=14)
plt.plot(x5,y5,color="#FF8066",marker="o",label="标准得分")
plt.grid(True)
plt.legend(loc="upper left")
plt.savefig("5.png")
print("得分结果为:")
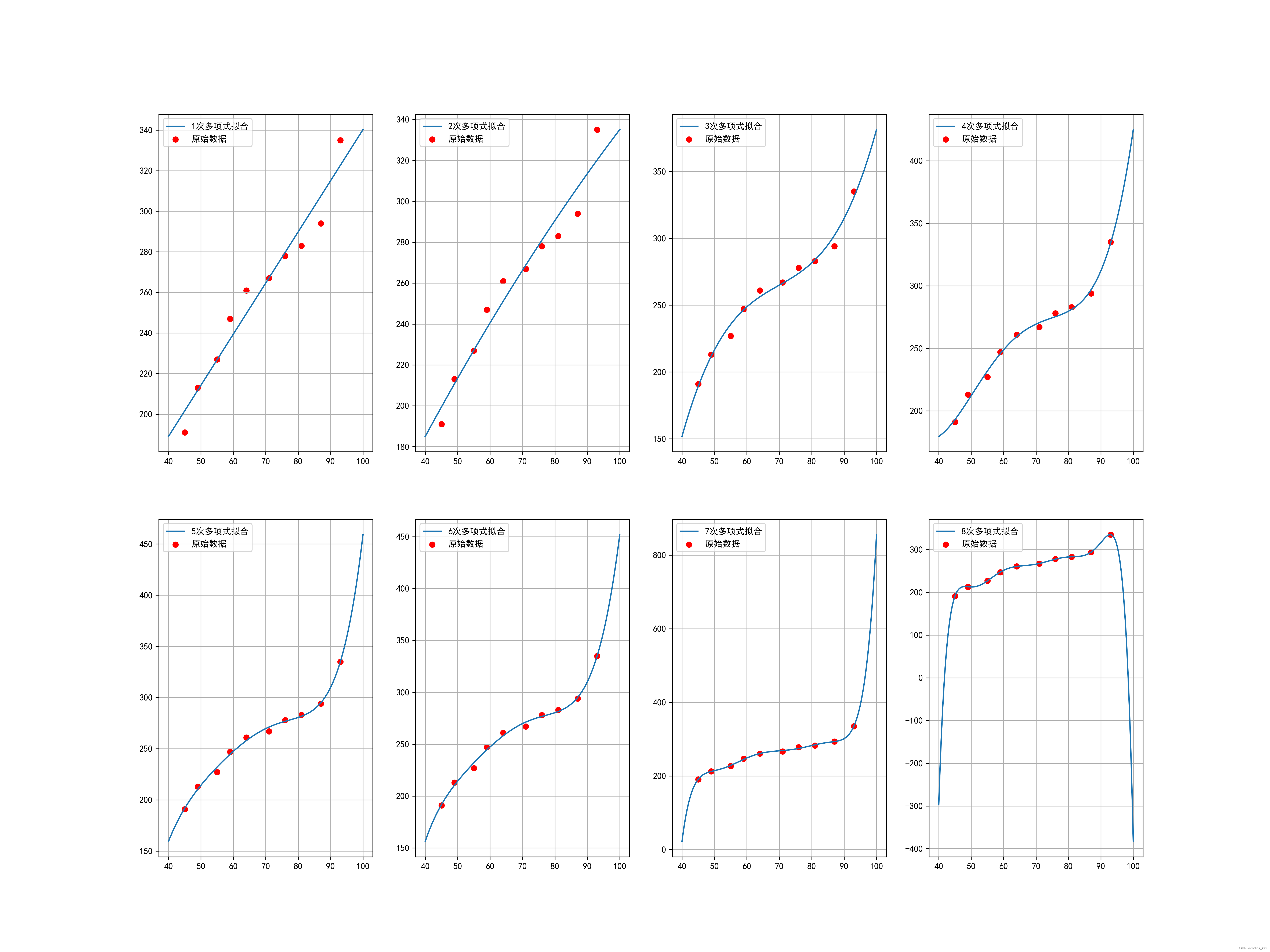
print(z)三、第二问(多项式拟合)

from scipy.interpolate import interp1d
import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics import r2_scoreplt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False #用来正常显示负号
plt.figure(figsize=(20,15),dpi=300)
plt.title("总成绩拟合图",fontsize=16)
plt.xlabel("体重",fontsize=14)
plt.ylabel("举重重量",fontsize=14)
for i in range(1,9):x_new = np.linspace(40, 100, 1000) # 生成新的x轴数据coefficients = np.polyfit(x3, y3, i) # 用5次多项式进行拟合poly = np.poly1d(coefficients) # 生成多项式函数# 绘图plt.subplot(2,4,i)plt.subplots_adjust(left=None, bottom=0.1, right=None, top=None,wspace=None, hspace=None)plt.grid(True)plt.scatter(x3,y3,marker="o",color="red", label='原始数据')plt.plot(x_new, poly(x_new), label=str(i)+'次多项式拟合')plt.legend(loc="upper left")
plt.savefig("2.png")# 计算拟合后的数值
for i in range(1,9):coefficients = np.polyfit(x3, y3, i) # 用5次多项式进行拟合poly = np.poly1d(coefficients) # 生成多项式函数y_poly = poly(x_new)# # 计算RMSE和MAE# rmse_cubic = np.sqrt(np.mean((y - f_cubic(x))**2))# mae_cubic = np.mean(np.abs(y - f_cubic(x)))rmse_poly = np.sqrt(np.mean((y3 - poly(x3))**2))mae_poly = np.mean(np.abs(y3 - poly(x3)))mape_poly=np.mean(np.abs(y3-poly(x3))/poly(x3))# 打印RMSE和MAEprint(str(i)+"次多项式拟合的RMSE和MAE分别为:{:.2f},{:.2f}".format(rmse_poly, mae_poly))print(str(i)+"次多项式拟合的MAPE分别为:{:.2f}".format(mape_poly))print(poly)y_poly = poly(x_new)# 计算R平方r2_poly = r2_score(y3, poly(x3))# 打印R平方print(str(i)+"次多项式拟合的R平方为:{:.2f}".format(r2_poly))print("\n")从上面的结果中我们可以看出,当多项式的最高次数大于4次的时后,虽然模型的R的平方较好,但是不符合实际情况,属于过拟合现象,上面的参数RMSE和MAE来计算误差的话,无法排除离群点的影响,所以采用了MAPE来计算误差的话,这样就排除离群点对模型的影响。这个多项式拟合可以用到第二问当中去,作为模型的改进,因此我们进行的优化为多项式优化。
可能大家会有疑问,为什么要用多项式拟合,而不去用其它函数呢?在这里就是用到泰勒公式的简单应用,用多项式近似地表示函数的公式称为泰勒公式,并且根据余项表达式的不同而有不同的形式。 得名于英国数学家布鲁克·泰勒,他在1712年的一封信里首次叙述了这个公式。嘿嘿这个大家大一的高数应该都是学过滴!
关于相关数学理论请看这篇文章(其实可以忽略,想了解的可以看下,记住结论就行,不用难为自己):
泰勒公式简单应用:多项式近似表示任意函数 - 知乎 (zhihu.com)
基于4次多项式的改进模型
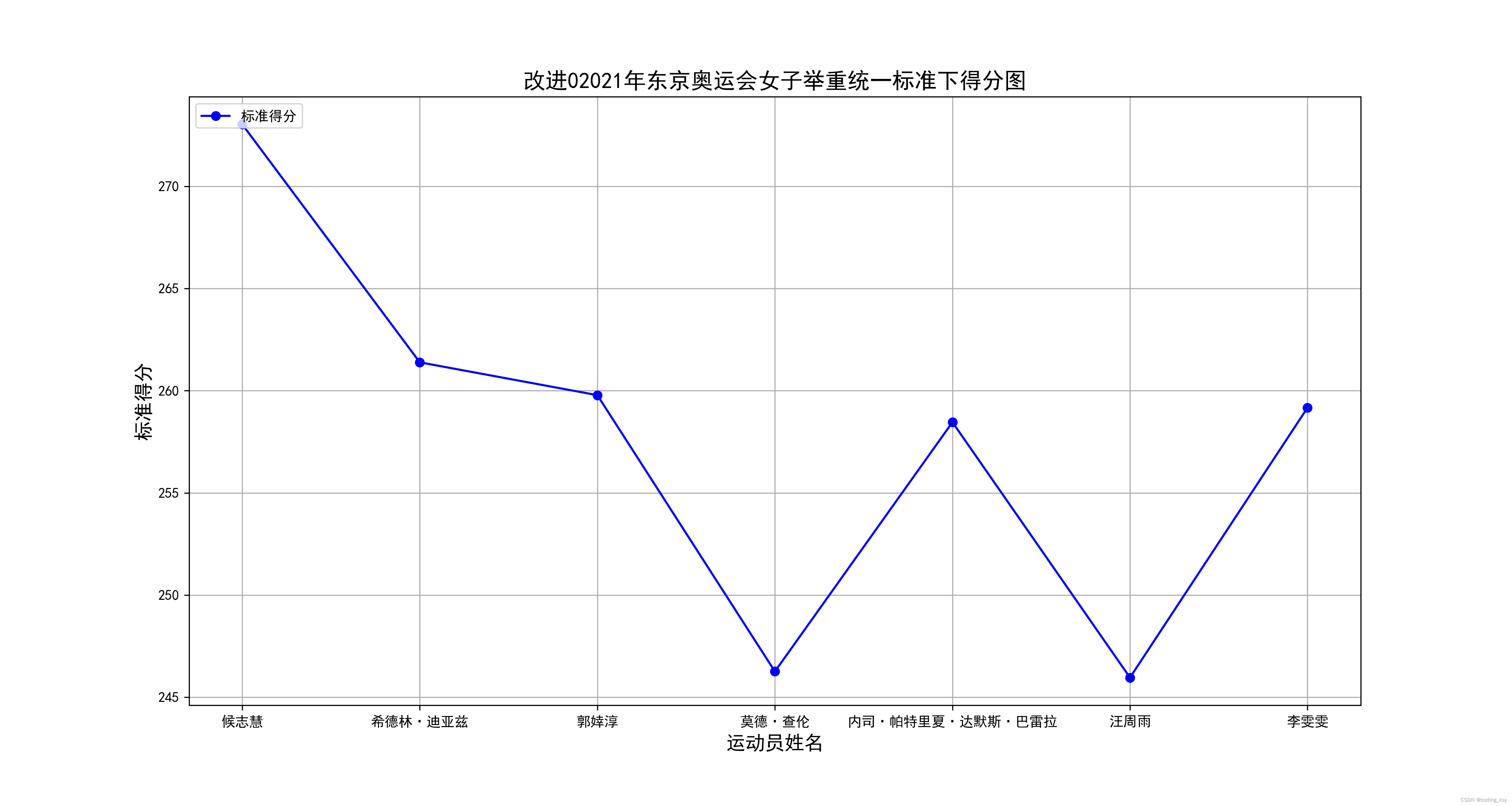
从图中可以清晰的看出:在4次多项式的条件下候志惠的标准的分最高。
为什么和前面的不一样呢?大家可能有疑问,但是在下面可以做一个实验,当多项式的最高次大于等于1时,模型所评选的女子冠军均为候志惠,这说明多项式的拟合精度更高,更加具有稳定性和可信性。
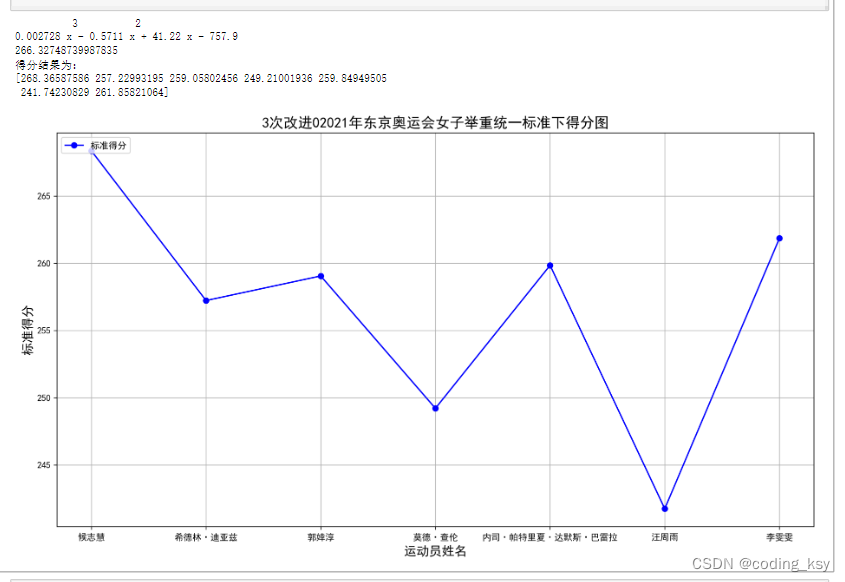
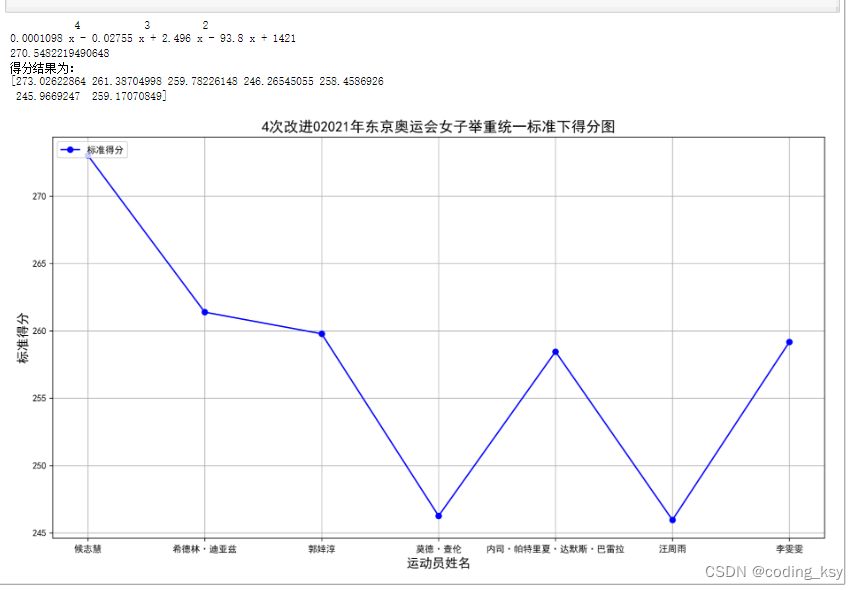
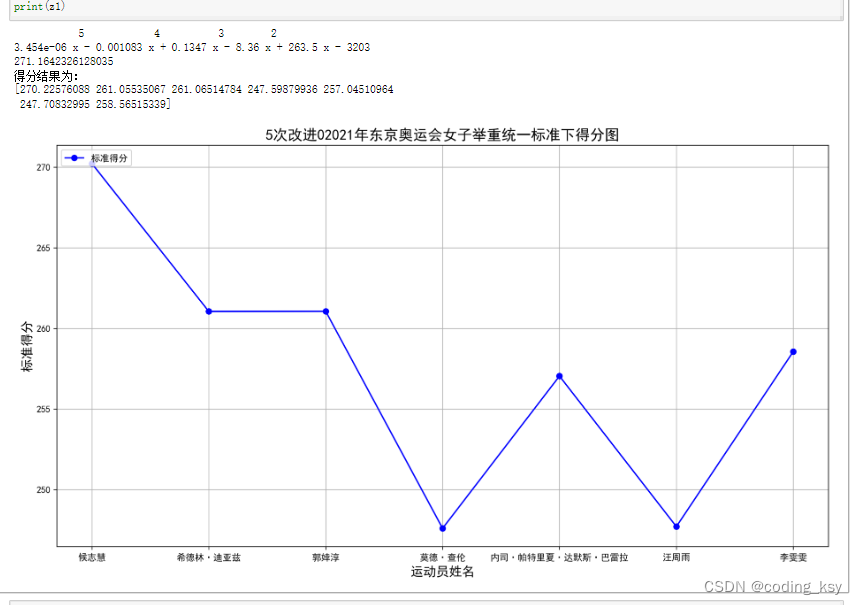
在这就不再一一列举了,从上面可以观察出随着最高次数的增加,模型逐渐趋于稳定。
代码:
#导库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt#读取数据
data=pd.read_excel("data.xlsx",sheet_name="东京奥运会女子举重")
x4=data["weight"].values
y4=data["power"].values#改进的模型,4次多项式拟合
coefficients = np.polyfit(x3, y3, 5) # 只需改动这里面参数,即可拟合多种多项式
poly = np.poly1d(coefficients) # 生成多项式函数
print(poly)
u=poly(71)
print(u)#定义改进后的标准得分函数
def zfunction(x,y):return (270.5482219490648*y)/poly(x)
z1=zfunction(x4,y4)#画图
x5=data["name"].values
y5=z1
plt.figure(figsize=(15,8),dpi=300)
plt.title("5次改进02021年东京奥运会女子举重统一标准下得分图",fontsize=16)
plt.xlabel("运动员姓名",fontsize=14)
plt.ylabel("标准得分",fontsize=14)
plt.plot(x5,y5,color="b",marker="o",label="标准得分")
plt.grid(True)
plt.legend(loc="upper left")
plt.savefig("6.png")
print("得分结果为:")
print(z1)至此解决重要的两问。三问、四问都比较容易解决。
四、第三问选取男女冠军
这一问就比较简单啦,在这里我就给大家说一种思路
首先按照上面的1、2问的思路对男子数据进行建模,选出男子冠军,然后再和我们选出的女子冠军进行比较,最后选出总冠军,关于比较的方法。
我查阅了相关资料:
‘’科学界对于男性与女性在青春期形成的生理差异已经普遍达成共识。在哈伯德已经经历过的男性青春期期间,男性的肌肉量会得到增加。
体育科学家塔克(Ross Tucker)称,男性青春期出现的一系列生理变化会(在男性与女性之间)带来显著的功能优势,他称在游泳与自行车运动上这种差异在10-12%之间,而在举重等涉及上肢肌肉力量的项目上可能达到“30-40%”这个结论我用往年的数据检验了,基本上是符合的,因此可以用了。
在模型假设部分:假设同体重下,男子的上肢力量要比女子高35%(这个比例位于30%-40%就行)。(这句话一定要带上)
即是选出的女子总冠军的标准化成绩乘上(1+0.35),再去和男子冠军的标准化成绩进行比较。根据我提供的数据男子标准到73kg、女子标准到71kg,由于男子的标准女子大,为了弥补这个差值,我们可以让女子和男子的上肢力量设置的大一些,也就是比0.35大一些,这样就弥补了这一缺陷啦。
代码上面都有了,直接套用就行。
四、第四问语文建模外加一些机理分析
这一问就更加简单了
这一问可以从摔跤、拳击、赛艇按体重分等级的体育项目来考虑
体测的男女的标准转化也是一个思路
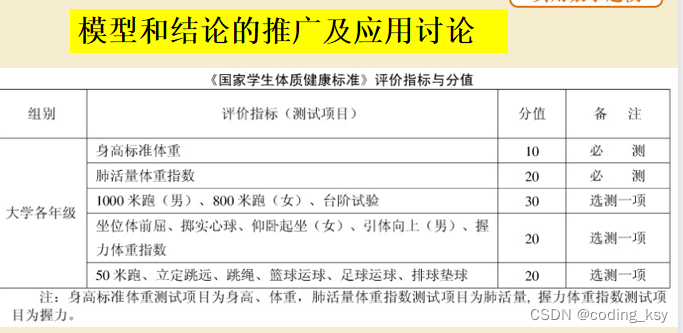
至此,全部更新完全,本人水平有限,如有错误,可以提出,欢迎交流。
相关文章:

女子举重问题
一、问题的描述 问题及要求 1、搜集各个级别世界女子举重比赛的实际数据。分别建立女子举重比赛总成绩的线性模型、幂函数模型、幂函数改进模型,并最终建立总冠军评选模型。 应用以上模型对最近举行的一届奥运会女子举重比赛总成绩进行排名,并对模型及…...

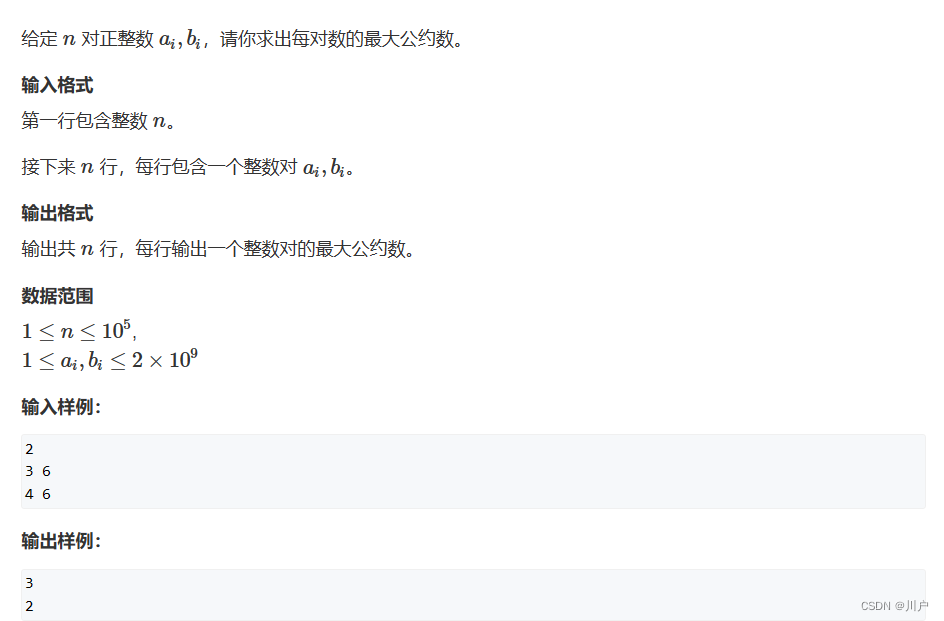
试题 历届真题 循环小数【第十一届】【决赛】【Python】
试题 历届真题 循环小数【第十一届】【决赛】【Python】 题目来源:第十一届蓝桥杯决赛 http://lx.lanqiao.cn/problem.page?gpidT2891 资源限制 内存限制:256.0MB C/C时间限制:1.0s Java时间限制:3.0s Python时间限制ÿ…...

关于类型转换
隐式转换先看个例子int a {500}; unsigned b {1000}; std::cout<<a-b;这里的输出结果并不为-500。因为最后输出结果的类型自动转换成了unsigned,unsigned是正整数型类型转换顺序表(由高到低)long doubledoublefloatunsigned long long long longunsigned long…...
蓝桥杯冲击-02约数篇(必考)
文章目录 前言 一、约数是什么 二、三大模板 1、试除法求约数个数 2、求约数个数 3、求约数之和 三、真题演练 前言 约数和质数一样在蓝桥杯考试中是在数论中考察频率较高的一种,在省赛考察的时候往往就是模板题,难度大一点会结合其他知识点考察&#x…...

122.(leaflet篇)leaflet地图图片之间存在缝隙
听老人家说:多看美女会长寿 地图之家总目录(订阅之前建议先查看该博客) 文章末尾处提供保证可运行完整代码包,运行如有问题,可“私信”博主。 存在缝隙–效果如下所示: 解决缝隙–效果如下所示: 下面献上完整代码,代码重要位置会做相应解释 <!DOCTYPE html>…...
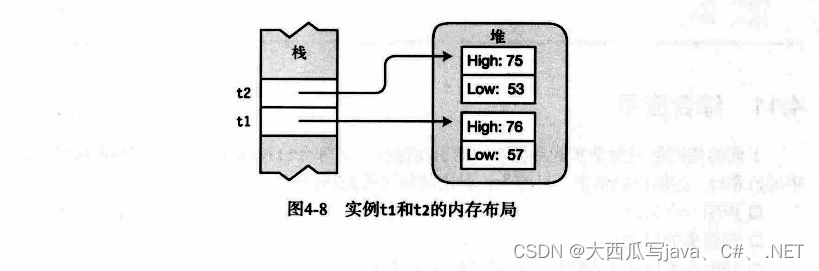
4.类的基本概念
目录 4.1 类的概述 类是一种活动的数据结构 4.2 程序和类:一个快速实例 4.3 声明类 4.4 类成员 4.4.1 字段 1.显示和隐式字段初始化 2. 声明多个字段 4.4.2 方法 4.5 创建变量和类的实例 4.6 为数据分配内存 合并这两个步骤 4.7 实例成员 4.8 访问修饰…...
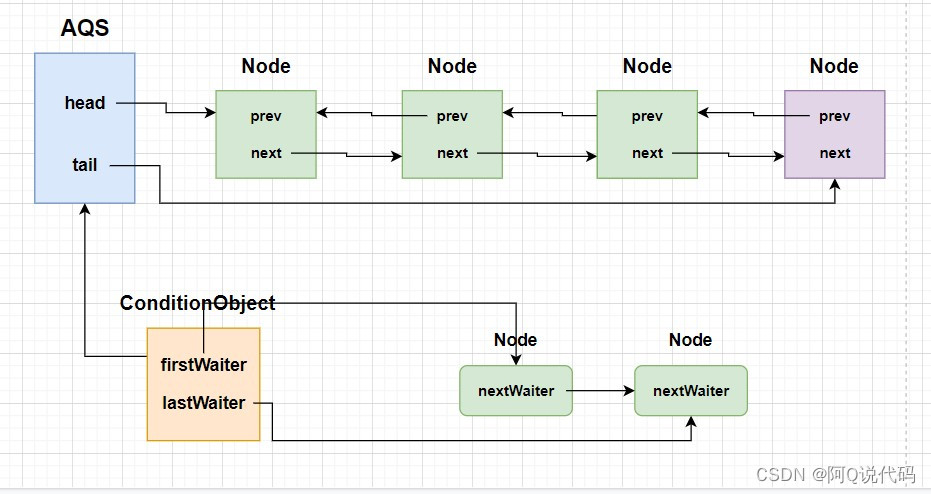
有图解有案例,我终于把 Condition 的原理讲透彻了
哈喽大家好,我是阿Q! 20张图图解ReentrantLock加锁解锁原理文章一发,便引发了大家激烈的讨论,更有小伙伴前来弹窗:平时加解锁都是直接使用Synchronized关键字来实现的,简单好用,为啥还要引用Re…...
Linux之找回root密码
文章目录前言一、启动系统二、进入编辑界面三、修改密码前言 当我们使用root用户登陆Linux时,忘记了登陆密码,改怎样修改登陆密码呢,接下来将介绍如何修改root密码 一、启动系统 首先,启动系统,进入开机界面&#x…...
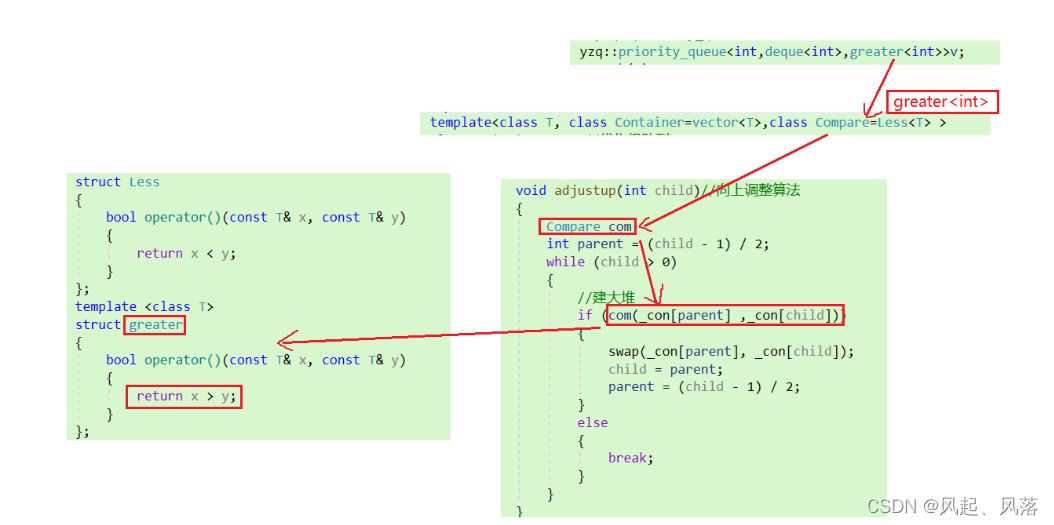
stack_queue | priority_queue | 仿函数
文章目录1. stack 的使用2. stack的模拟实现3. queue的使用4. queue的模拟实现5. deque ——双端队列deque优缺点6. priority_queue ——优先级队列1. priority_queue的使用2. priority_queue的模拟实现push——插入pop ——删除top —— 堆顶仿函数问题完整代码实现1. stack 的…...
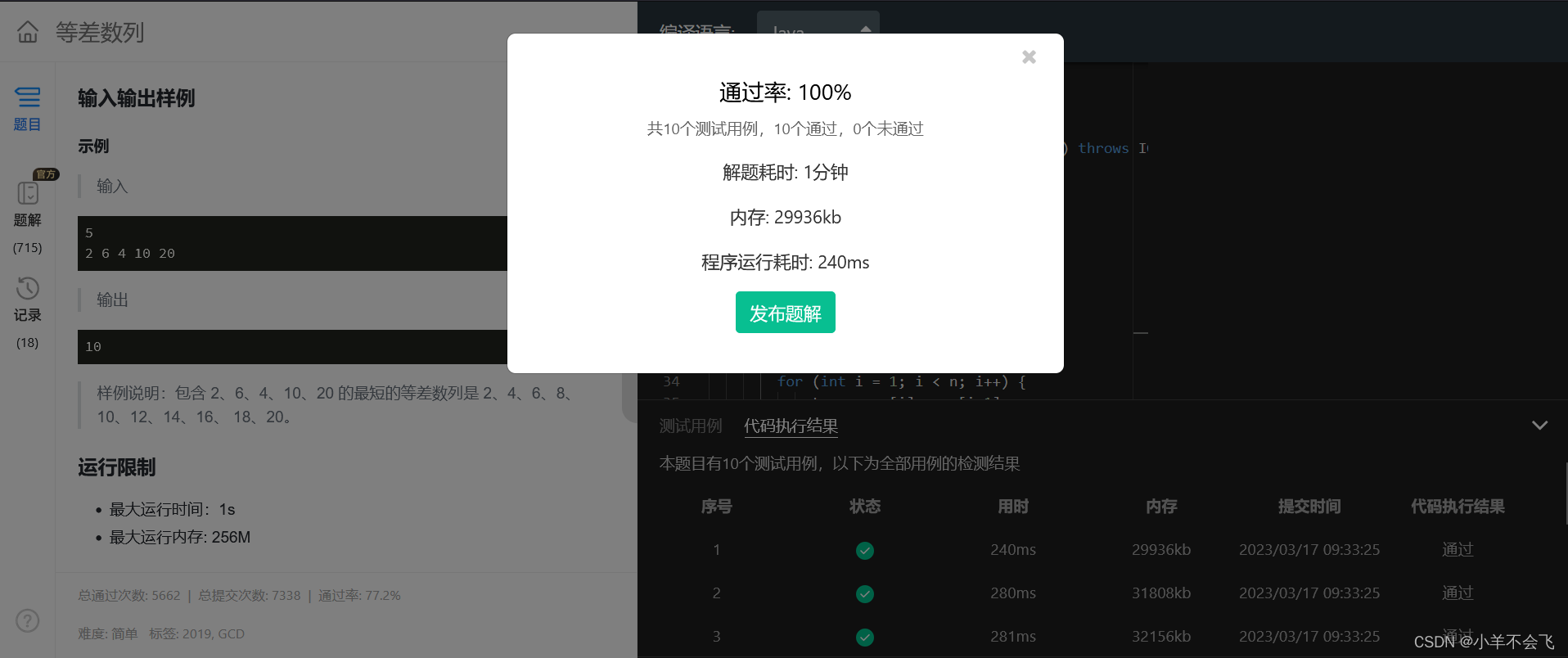
第十四届蓝桥杯三月真题刷题训练——第 14 天
目录 第 1 题:组队 题目描述 运行限制 代码: 第 2 题:不同子串 题目描述 运行限制 代码: 思路: 第 3 题:等差数列 题目描述 输入描述 输出描述 输入输出样例 运行限制 代码: 思…...
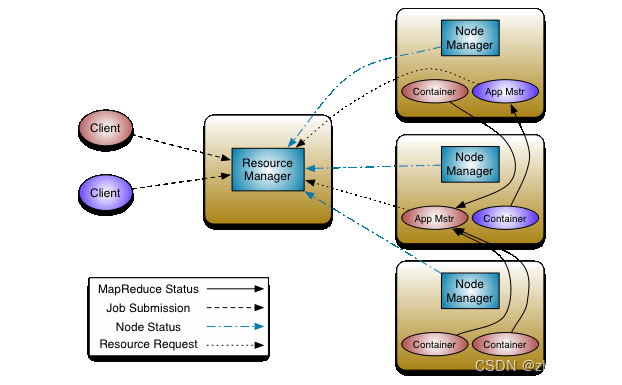
【Hadoop-yarn-01】大白话讲讲资源调度器YARN,原来这么好理解
YARN作为Hadoop集群的御用调度器,在整个集群的资源管理上立下了汗马功劳。今天我们用大白话聊聊YARN存在意义。 有了机器就有了资源,有了资源就有了调度。举2个很鲜活的场景: 在单台机器上,你开了3个程序,分别是A、B…...
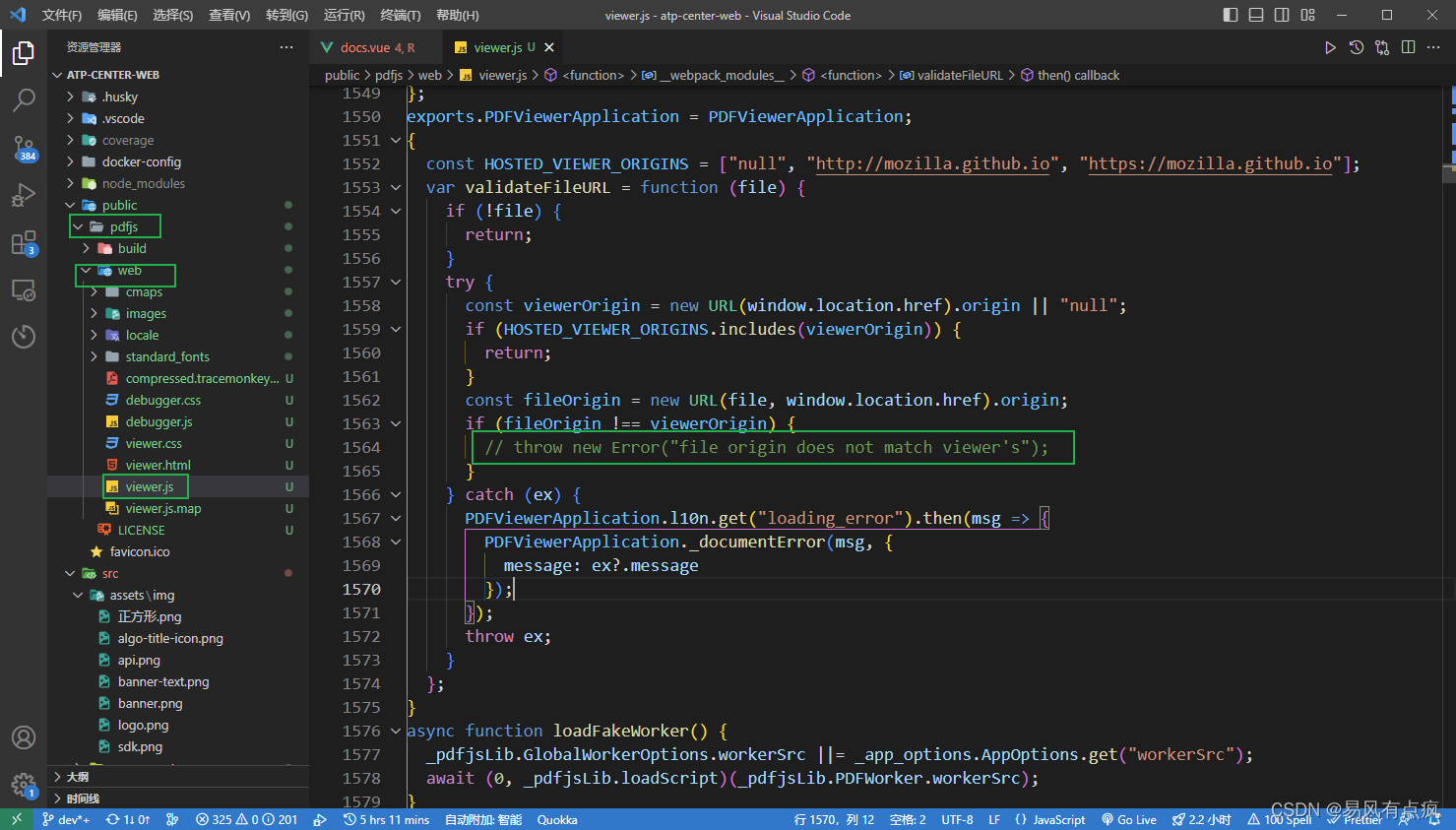
技术掉:PDF显示,使用pdf.js
PDF 显示 场景: 其实直接显示 pdf 可以用 iframe 标签,但产品觉得浏览器自带的 pdf 预览太丑了,而且无法去除那些操作栏。 解决方案:使用 pdf.js 进行显示 第一步:引入 pdf.js 去官网下载稳定版的 pdf.js 文件 然后…...
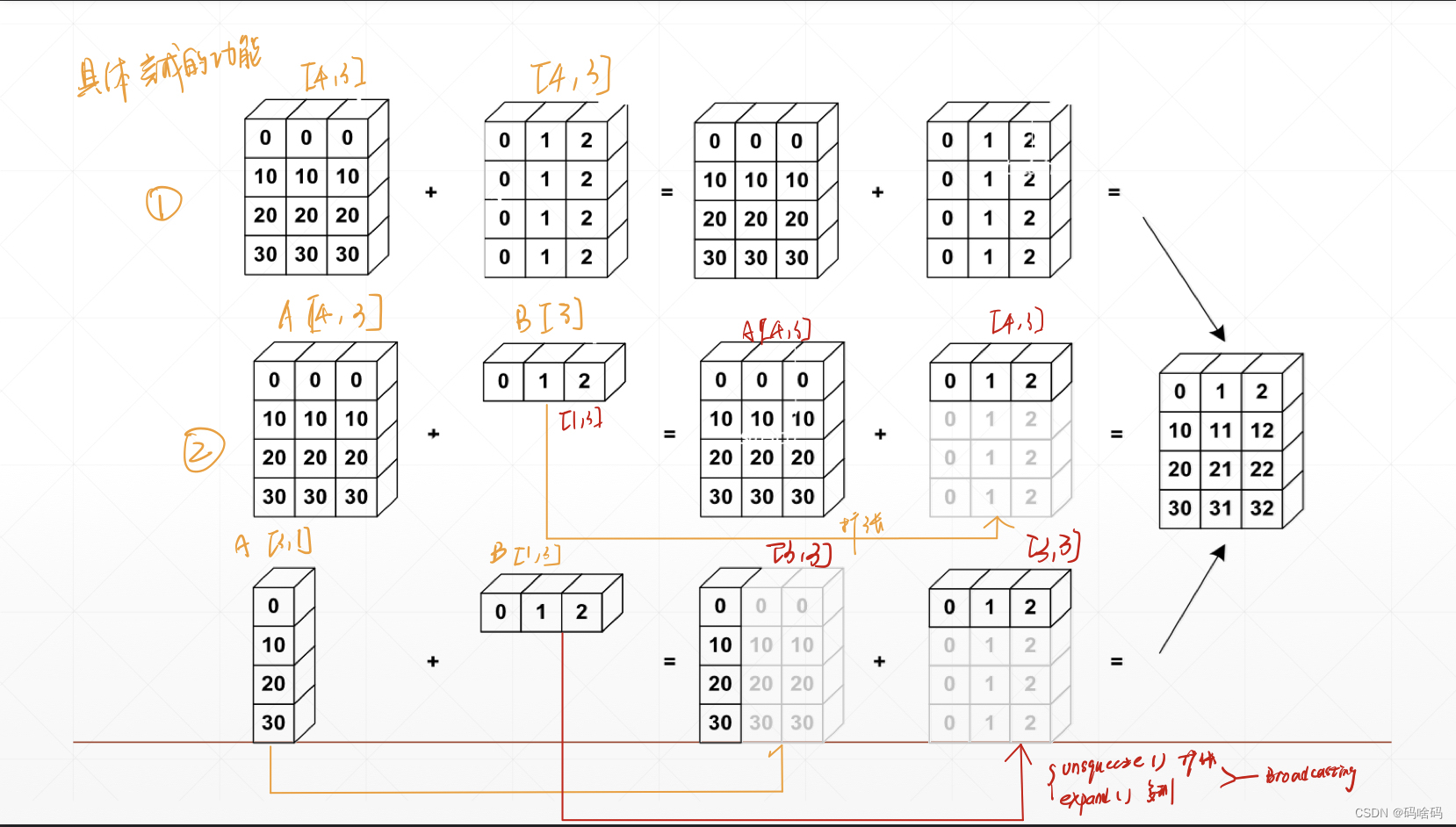
有关pytorch的一些总结
Tensor 含义 张量(Tensor):是一个多维数组,它是标量、向量、矩阵的高维拓展。 创建 非随机创建 1.用数组创建 将数组转化为tensor np.ones([a,b]) 全为1 #首先导入PyTorch import torch#数组创建 import numpy as np anp.arr…...
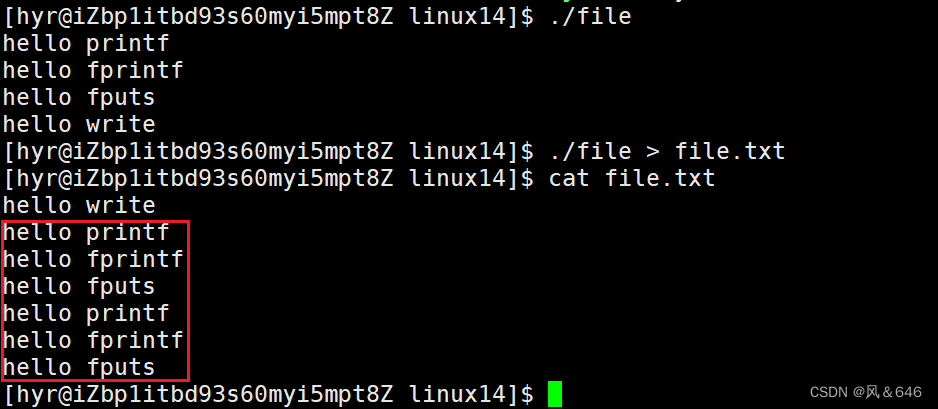
基础IO【Linux】
文章目录:文件相关知识C语言文件IOstdin & stdout & stderr系统文件 IOopenclosewriteread文件描述符文件描述符的分配规则重定向dup2系统调用FILEFILE中的文件描述符FILE中的缓冲区理解文件相关知识 文件 文件内容 文件属性(每一个已经存在的…...
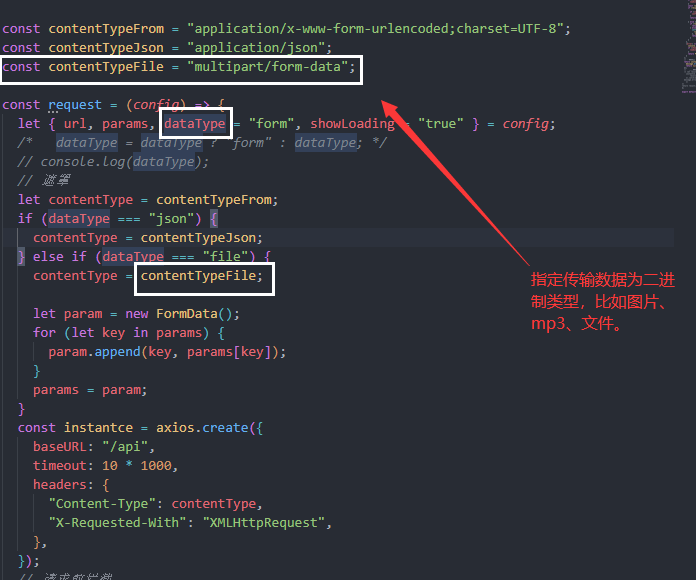
Vue3——自定义封装上传图片样式
自定义封装上传图片样式 一、首先需要新建一个自组建完善基础的结构,我这里起名为ImgUpload.vue <el-upload name"file" :show-file-list"false" accept".png,.PNG,.jpg,.JPG,.jpeg,.JPEG,.gif,.GIF,.bmp,.BMP" :multiple"…...
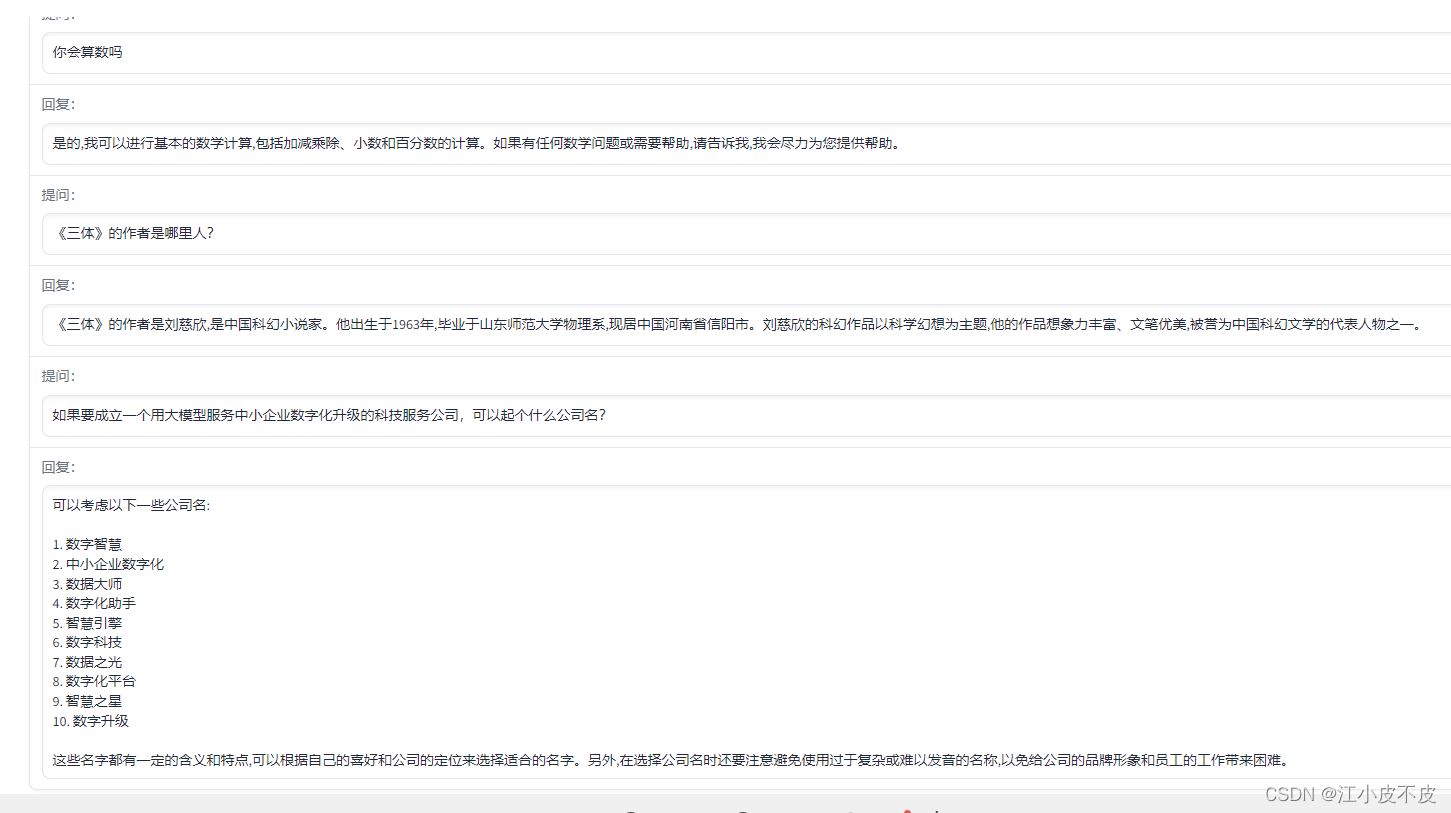
ChatGLM-6B (介绍以及本地部署)
中文ChatGPT平替——ChatGLM-6BChatGLM-6B简介官方实例本地部署1.下载代码2.通过conda创建虚拟环境3.修改代码4.模型量化5.详细代码调用示例ChatGLM-6B 简介 ChatGLM-6B 是一个开源的、支持中英双语问答的对话语言模型,基于 General Language Model (GLM) 架构&…...
react的基础使用
react中为什么使用jsxReact 认为渲染逻辑本质上与其他 UI 逻辑内在耦合,比如,在 UI 中需要绑定处理事件、在某些时刻状态发生变化时需要通知到 UI,以及需要在 UI 中展示准备好的数据。react认为将业务代码和数据以及事件等等 需要和UI高度耦合…...

letcode 4.寻找两个正序数组的中位数(官方题解笔记)
题目描述 给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。 算法的时间复杂度应该为 O(log (mn)) 。 1.二分查找 1.1思路 时间复杂度:O(log(mn)) 空间复杂度:O(1) 给定…...
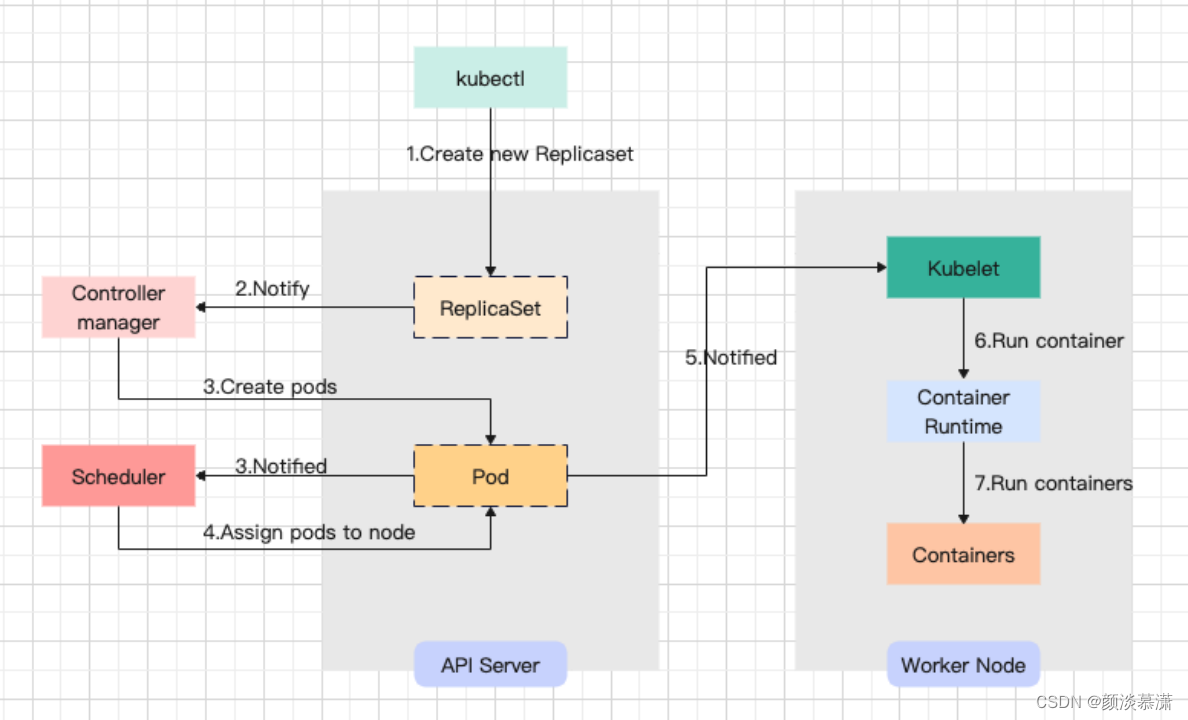
【面试题系列】K8S常见面试题
目录 序言 问题 1. 简单说一下k8s集群内外网络如何互通的吧 2.描述一下pod的创建过程 3. 描述一下k8s pod的终止过程 4.Kubernetes 中的自动伸缩有哪些方式? 5.Kubernetes 中的故障检测有哪些方式? 6.Kubernetes 中的资源调度有哪些方式ÿ…...

字符函数和字符串函数(上)-C语言详解
CSDN的各位友友们你们好,今天千泽为大家带来的是C语言中字符函数和字符串函数的详解,掌握了这些内容能够让我们更加灵活的运用字符串,接下来让我们一起走进今天的内容吧!写这篇文章需要在cplusplus.com上大量截图,十分不易!如果对您有帮助的话希望能够得到您的支持和帮助,我会持…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...
