汉明权重(Hamming Weight)(统计数据中1的个数)VP-SWAR算法
汉明权重(Hamming Weight)(统计数据中1的个数)VP-SWAR算法
定义
汉明重量是一串符号中非零符号的个数。它等于同样长度的全零符号串的汉明距离(在信息论中,两个等长字符串之间的汉明距离等于两个字符串对应位置的不同字符的个数)。
汉明重量在常见的数据位符号串中,它是1的个数。
算法思想
基于分治的算法,将n位二进制进行分组,通过一系列位移和位运算操作,可以在常数时间内计算多个字节的汉明重量,并且不需要使用额外的内存。
简化示例
假设一个8bit的2进制串 x=abcd,efgh其中a-b 属于{0,1}
求解的输出是 ans = a+b+c+d+e+f+g+h
step1. 2bits m1= 0101 0101
x&m1 = 0b0d 0f0h
(x>>1)&m1 = 0a0c 0e0g
求和得到[a+b]_2[c+d]_2 [e+f]_2[g+h]_2,这里[x]_2表示2位二进制中1的个数
step2. 4bits m2 = 0011 0011
x&m2 = 00[c+d]_2 00[g+h]_2
(x>>2)&m2 = 00[a+b]_2 00[e+f]_2
求和得到[a+b+c+d]_4 [e+f+g+h]_4
step3. 8bits m4 = 0000 1111
x&m4 = 0000 [e+f+g+h]_4
(x>>4)&m4 = 0000 [a+b+c+d]_4
求和得到 [a+b+c+d+e+f+g+h]_8
对应的十进制值就是最终的答案
算法实现 variable-precision SWAR算法
const uint64_t m1 = 0x5555555555555555; //binary: 0101...
const uint64_t m2 = 0x3333333333333333; //binary: 00110011..
const uint64_t m4 = 0x0f0f0f0f0f0f0f0f; //binary: 4 zeros, 4 ones ...
const uint64_t m8 = 0x00ff00ff00ff00ff; //binary: 8 zeros, 8 ones ...
const uint64_t m16 = 0x0000ffff0000ffff; //binary: 16 zeros, 16 ones ...
const uint64_t m32 = 0x00000000ffffffff; //binary: 32 zeros, 32 ones
const uint64_t h01 = 0x0101010101010101; //the sum of 256 to the power of 0,1,2,3...//This is a naive implementation, shown for comparison,
//and to help in understanding the better functions.
//This algorithm uses 24 arithmetic operations (shift, add, and).
// 朴素算法
int popcount64a(uint64_t x)
{x = (x & m1 ) + ((x >> 1) & m1 ); //put count of each 2 bits into those 2 bits x = (x & m2 ) + ((x >> 2) & m2 ); //put count of each 4 bits into those 4 bits x = (x & m4 ) + ((x >> 4) & m4 ); //put count of each 8 bits into those 8 bits x = (x & m8 ) + ((x >> 8) & m8 ); //put count of each 16 bits into those 16 bits x = (x & m16) + ((x >> 16) & m16); //put count of each 32 bits into those 32 bits x = (x & m32) + ((x >> 32) & m32); //put count of each 64 bits into those 64 bits return x;
}详细步骤
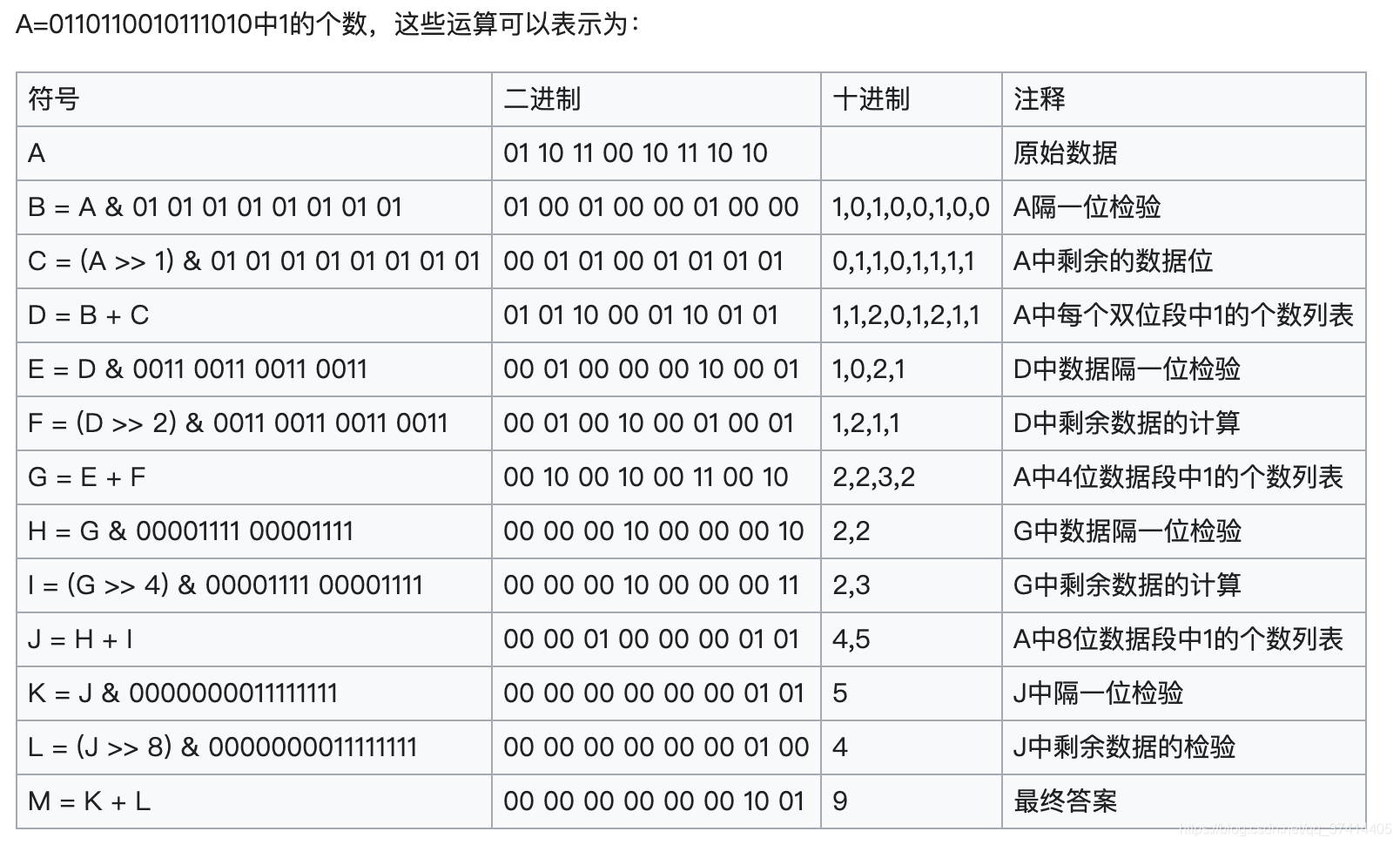
优化算法
//This is better when most bits in x are 0
//This algorithm works the same for all data sizes.
//This algorithm uses 3 arithmetic operations and 1 comparison/branch per "1" bit in x.
// 适用于0比较多的数
// 数字 n中最低位的 1 总是对应 n - 1 中的 0
// 将 n 和 n - 1 进行与运算总是能把 n 中最低位的 1 变成 0,并保持其他位不变
int popcount64d(uint64_t x)
{int count;for (count=0; x; count++)x &= x - 1;return count;
}// 常用写法
int hammingWeight(uint32_t n) {int count = 0;while( n ){count ++;n &= n-1;}return count;
}// 查表法 用空间换时间 从而得到O(1)的最优算法
// 以4bit的串为例,可以构造一个数组int counts[16]={0,1,1,2,1,2,2,3,1,2,2,3,2,3,3,4}.
// 对于4bit的x, x的hamming weight为:counts[x].
static unsigned char wordbits[65536] = { bitcounts of ints between 0 and 65535 };
static int popcount(uint32 i)
{return (wordbits[i&0xFFFF] + wordbits[i>>16]);
}参考
Hamming weight WIKI
汉明权重(hamming weight) ----- 计算数据位中1的个数
相关文章:

汉明权重(Hamming Weight)(统计数据中1的个数)VP-SWAR算法
汉明权重(Hamming Weight)(统计数据中1的个数)VP-SWAR算法 定义 汉明重量是一串符号中非零符号的个数。它等于同样长度的全零符号串的汉明距离(在信息论中,两个等长字符串之间的汉明距离等于两个字符串对应位置的不同…...

基于 PyTorch 的模型瘦身三部曲:量化、剪枝和蒸馏,让模型更短小精悍!
基于 PyTorch 的模型量化、剪枝和蒸馏 1. 模型量化1.1 原理介绍1.2 PyTorch 实现 2. 模型剪枝2.1 原理介绍2.2 PyTorch 实现 3. 模型蒸馏3.1 原理介绍3.2 PyTorch 实现 参考文献 1. 模型量化 1.1 原理介绍 模型量化是将模型参数从高精度(通常是 float32࿰…...

二、原型模式
文章目录 1 基本介绍2 实现方式深浅拷贝目标2.1 使用 Object 的 clone() 方法2.1.1 代码2.1.2 特性2.1.3 实现深拷贝 2.2 在 clone() 方法中使用序列化2.2.1 代码 2.2.2 特性 3 实现的要点4 Spring 中的原型模式5 原型模式的类图及角色5.1 类图5.1.1 不限制语言5.1.2 在 Java 中…...

【目标检测】Anaconda+PyTorch(GPU)+PyCharm(Yolo5)配置
前言 本文主要介绍在windows系统上的Anaconda、PyTorch、PyCharm、Yolov5关键步骤安装,为使用yolo所需的环境配置完善。同时也算是记录下我的配置流程,为以后用到的时候能笔记查阅。 Anaconda 软件安装 Anaconda官网:https://www.anaconda…...

Django实战项目之进销存数据分析报表——第二天:项目创建和 PyCharm 配置
在上一篇博客中,我们讨论了如何搭建一个全栈 Web 应用的开发环境,包括 Python 环境的创建、Django 和 MySQL 的安装以及前端技术栈的选择。现在,让我们继续深入,学习如何在 PyCharm 中创建一个新的 Django 项目并进行配置。 一…...

静态路由实验
1.实验拓扑图 二、实验要求 1.R6为ISP,接口IP地址均为公有地址,该设备只能配置IP地址,之后不能再对其进行任何配置; 2.R1-R5为局域网,私有IP地址192.168.1.0/24,请合理分配; 3.R1、R2、R4&…...

VSCode STM32嵌入式开发插件记录
要卸载之前搭建的VSCode嵌入式开发环境了,记录一下用的插件。 1.Cortex-Debug https://github.com/Marus/cortex-debug 2.Embedded IDE https://github.com/github0null/eide 3.Keil uVision Assistant https://github.com/jacksonjim/keil-assistant/ 4.RTO…...

linux cpu 占用超100% 分析。
感谢: https://www.cnblogs.com/wolfstark/p/16450131.html 总结: 查看进程中各个线程占用百分比 top -H -p <pid> 某线程100%了 说明 任务处理不过来 会卡 但是永远不可能超100% 系统监视器里面看到的是 所有线程占用的 总和会超100%。 所以最好的情况是&…...

自然学习法和科学学习法
一、自然学习法 自然学习法:什么事自然学习法,特意让kimi来回答了一下。所谓的自然学习法说的俗一点就是野路子学习方法。这种学习方法的特点是“慢”“没有系统性”,学完之后感觉都会了,但是又感觉什么都不会。 二、科学学习法 …...
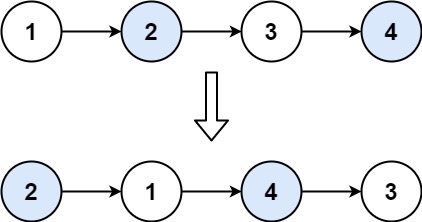
力扣第二十四题——两两交换链表中的节点
内容介绍 给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题(即,只能进行节点交换)。 示例 1: 输入:head [1,2,3,4] 输出ÿ…...

C语言柔性数组详解
目录 1.柔性数组 2.柔性数组的特点 3.柔性数组的使用 4.柔性数组的优势 1.柔性数组 C99 中,结构体中的最后一个元素允许是未知大小的数组,这就叫做『柔性数组』成员。 例如: struct S {char c;int n;int arr[];//柔性数组 }; struct …...
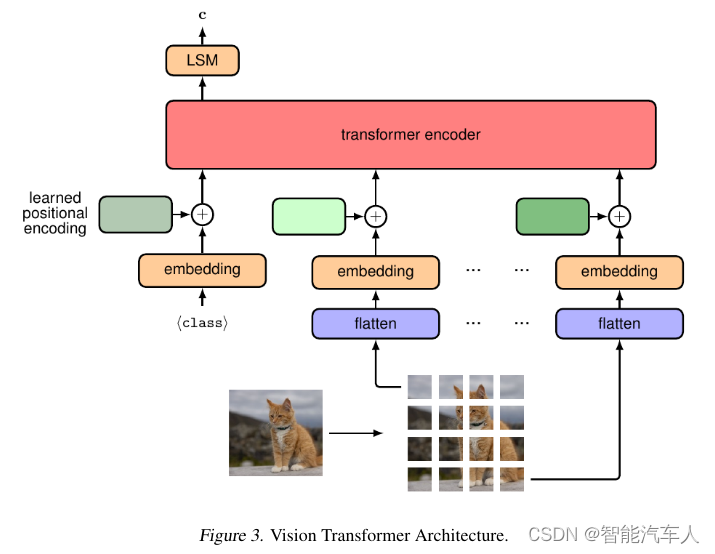
自动驾驶---视觉Transformer的应用
1 背景 在过去的几年,随着自动驾驶技术的不断发展,神经网络逐渐进入人们的视野。Transformer的应用也越来越广泛,逐步走向自动驾驶技术的前沿。笔者也在博客《人工智能---什么是Transformer?》中大概介绍了Transformer的一些内容:…...

预训练语言模型实践笔记
Roberta output_hidden_statesTrue和last_hidden_states和pooler_output 在使用像BERT或RoBERTa这样的transformer模型时,output_hidden_states和last_hidden_state是两个不同的概念。 output_hidden_states: 这是一个布尔值,决定了模型是否应该返回所…...

Perl 哈希
Perl 哈希 Perl 哈希是一种强大的数据结构,用于存储键值对集合。它是 Perl 语言的核心特性之一,广泛应用于各种编程任务中。本文将详细介绍 Perl 哈希的概念、用法和最佳实践。 什么是 Perl 哈希? Perl 哈希是一种关联数组,其中…...

Linux之Mysql索引和优化
一、MySQL 索引 索引作为一种数据结构,其用途是用于提升数据的检索效率。 1、索引分类 - 普通索引(INDEX):索引列值可重复 - 唯一索引(UNIQUE):索引列值必须唯一,可以为NULL - 主键索引(PRIMARY KEY):索引列值必须唯一,不能为NULL,一个表只能有一个主键索引 - 全…...

springboot业务逻辑写在controller层吗
Spring Boot中的业务逻辑不应该直接写在Controller层。 在Spring Boot项目中,通常将业务逻辑分为几个层次,包括Controller层、Service层、Mapper层和Entity层。 1.其中,Controller层主要负责处理HTTP请求,通过注…...

Ubuntu 24.04 LTS 桌面安装MT4或MT5 (MetaTrader)教程
运行脚本即可在 Ubuntu 24.04 LTS Noble Linux 上轻松安装 MetaTrader 5 或 4 应用程序,使用 WineHQ 进行外汇交易。 MetaTrader 4 (MT4) 或 MetaTrader 5 是用于交易外汇对和商品的流行平台。它支持各种外汇经纪商、内置价格分析工具以及通过专家顾问 (EA) 进行自…...

Go基础编程 - 12 -流程控制
流程控制 1. 条件语句1.1. if...else 语句1.2. switch 语句1.3. select 语句1.3.1. select 语句的通信表达式1.3.2. select 的基特性1.3.3. select 的实现原理1.3.4. 经典用法1.3.4.1 超时控制1.3.4.2 多任务并发控制1.3.4.3 监听多通道消息1.3.4.4 default 实现非堵塞读写 2. …...

汽车信息安全--TLS,OpenSSL
目录 TLS相关知识 加密技术 对称加密 非对称加密 数字签名和CA 信任链 根身份证和自签名 双方TLS认证 加密和解密的性能 TLS相关知识 加密技术 TLS依赖两种加密技术 1. 对称加密(symmetric encryption) 2. 非对称加密(asymmetri…...
与左模糊匹配(LIKE LEFT))
深入探索 SQL 中的 LIKE 右模糊匹配(LIKE RIGHT)与左模糊匹配(LIKE LEFT)
引言 在数据库操作中,LIKE 子句是执行模糊搜索的强大工具,用于匹配列中的数据与指定的模式。本文将详细介绍 LIKE 子句中的两种常用模式:右模糊匹配(LIKE RIGHT)和左模糊匹配(LIKE LEFT)&#…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...
