CF1784D Wooden Spoon
CF1784D Wooden Spoon
题目大意
有2n2^n2n个人,进行nnn轮比赛。比赛的图是一棵完全二叉树。编号小的人一定能赢编号大的人,如果一个人满足:
- 第一次比赛被打败
- 打败这个人的人在第二次比赛中被打败
- 打败上一个人的人在第三次比赛中被打败
- …\dots…
- 打败上一个人的人在最后一次比赛中被打败
那么这个人就能得到安慰奖。
求对于每个人,有多少种编号的排列来比赛(叶子的排列),使得他能得安慰奖。输出答案模998244353998244353998244353。
题解
我们按照题意来构建这棵二叉树,叶子节点就是这个序列,而非叶子节点的权值就是其子树中权值最大的点的权值。假如编号为kkk的点能拿安慰奖,那么这个点到根的路径上的点的权值一定是单调递减的。
假设这个点到根的权值组成的序列为a0,a1…,ana_0,a_1\dots,a_na0,a1…,an,我们依次来看每个点的贡献。
aia_iai的贡献为C(2n−ai−2i−1,2i−1−1)×(2i−1)!C(2^n-a_i-2^{i-1},2^{i-1}-1)\times (2^{i-1})!C(2n−ai−2i−1,2i−1−1)×(2i−1)!。也就是说,这个点在没有kkk的那棵子树中还要放小于他的2i−1−12^{i-1}-12i−1−1个点。因为要小于aia_iai,而且自己是一定要选的,所以要减aia_iai。又因为有kkk的那一边的点不能选,所以要减2i−12^{i-1}2i−1。这棵子树内的点的顺序可以任意排列,所以要乘上(2i−1)!(2^{i-1})!(2i−1)!。
设fi,sf_{i,s}fi,s表示第iii个数为sss时第iii个数到第nnn个数的贡献,gi,sg_{i,s}gi,s表示第iii个数小于等于sss时第iii个数到第nnn个数的贡献和。那么转移式为
fi,s=gi+1,s−1×C(2n−s−2i−1,2i−1−1)×(2i−1)!f_{i,s}=g_{i+1,s-1}\times C(2^n-s-2^{i-1},2^{i-1}-1)\times (2^{i-1})!fi,s=gi+1,s−1×C(2n−s−2i−1,2i−1−1)×(2i−1)!
gi,s=gi,s−1+fi,sg_{i,s}=g_{i,s-1}+f_{i,s}gi,s=gi,s−1+fi,s
因为kkk的位置任意,所以最后还要乘上2n2^n2n。那么编号为kkk的点的答案就是g1,k−1×2ng_{1,k-1}\times 2^ng1,k−1×2n。
时间复杂度为O(n×2n)O(n\times 2^n)O(n×2n)。
code
#include<bits/stdc++.h>
using namespace std;
const int N=1<<20;
int n;
long long jc[N+5],ny[N+5];
long long f[25][N+5],g[25][N+5];
long long mod=998244353;
long long mi(long long t,long long v){if(!v) return 1;long long re=mi(t,v/2);re=re*re%mod;if(v&1) re=re*t%mod;return re;
}
void init(){jc[0]=1;for(int i=1;i<=N;i++) jc[i]=jc[i-1]*i%mod;ny[N]=mi(jc[N],mod-2);for(int i=N-1;i>=0;i--) ny[i]=ny[i+1]*(i+1)%mod;
}
long long C(int x,int y){if(x<y) return 0;return jc[x]*ny[y]%mod*ny[x-y]%mod;
}
int main()
{init();scanf("%d",&n);for(int s=1;s<=(1<<n);s++){f[n][s]=C((1<<n)-s-(1<<n-1),(1<<n-1)-1)*jc[1<<n-1]%mod;g[n][s]=(g[n][s-1]+f[n][s])%mod;}for(int i=n-1;i>=1;i--){for(int s=1;s<=(1<<n);s++){f[i][s]=g[i+1][s-1]*C((1<<n)-s-(1<<i-1),(1<<i-1)-1)%mod*jc[1<<i-1]%mod;g[i][s]=(g[i][s-1]+f[i][s])%mod;}}for(int s=1;s<=(1<<n);s++){printf("%lld\n",g[1][s-1]*(1<<n)%mod);}return 0;
}
相关文章:

CF1784D Wooden Spoon
CF1784D Wooden Spoon 题目大意 有2n2^n2n个人,进行nnn轮比赛。比赛的图是一棵完全二叉树。编号小的人一定能赢编号大的人,如果一个人满足: 第一次比赛被打败打败这个人的人在第二次比赛中被打败打败上一个人的人在第三次比赛中被打败…\d…...
【数据结构】栈
文章目录😺前言栈初始化栈顶入栈栈顶出栈栈体判空栈的数据个数获取栈顶元素栈的销毁整体代码😼写在最后😺前言 👻前面我们学习了链表,总算是跨过一个台阶了,本章带大家轻松一波,领悟一下栈的魅力…...
C++单继承和多继承
C单继承和多继承继承单继承写法继承中构造函数的写法写法构造和析构的顺序问题多继承继承 1.继承,主要是遗传学中的继承概念 2.继承的写法,继承中的权限问题 3.继承中的构造函数的写法 继承:子类没有新的属性,或者行为的产生 父类…...
金三银四,今年企业招聘如何?
又是一年求职季,互联网人找工作,和找对象一样严谨,不随便放手更不随便牵手。于是挑挑拣拣,最后的结果可能就是把自己挑剩下了。 时间已经悄然滑进3月中旬,多少无处安放的青春,还没尘埃落定?优秀…...

数字信号处理:滤波、频谱
一、滤波算法 应该说数字滤波器可以有效减小50Hz工频的干扰,完全消除是不可能的。以20ms为最小单位的整倍数周期滤波,可以有效减少工频的干扰。 软件中构建 IIR 陷波或者 FIR 带阻 数字滤波器,消除工频干扰对测量结果的影响。 1. 自适应滤波 …...
C#等高级语言运行过程
C#等高级语言运行流程:假设您编写了一个 C# 程序并将其保存在一个称为源代码的文件中。特定于语言的编译器将源代码编译成 MSIL(Microsoft 中间语言),也称为 CIL(通用中间语言)或 IL(中间语言&a…...
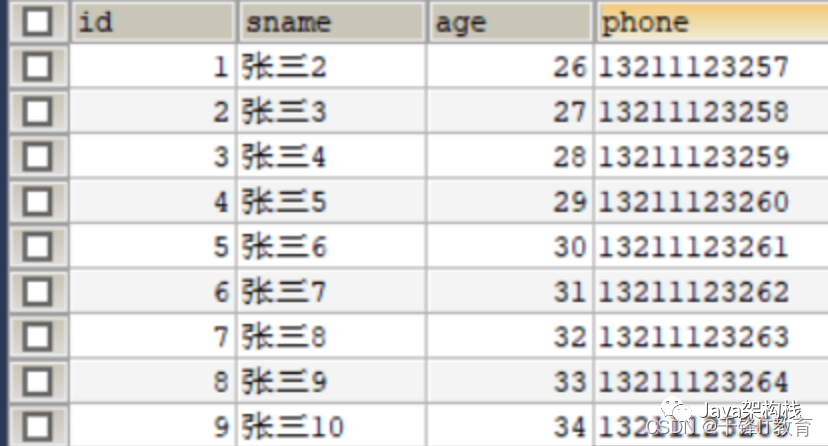
如何优雅的用POI导入Excel文件
在企业级项目开发中,要经常涉及excel文件和程序之间导入导出的业务要求,那么今天来讲一讲excel文件导入的实现。java实现对excel的操作有很多种方式,例如EasyExcel等,今天我们使用的是POI技术实现excel文件的导入。POI技术简介1.P…...
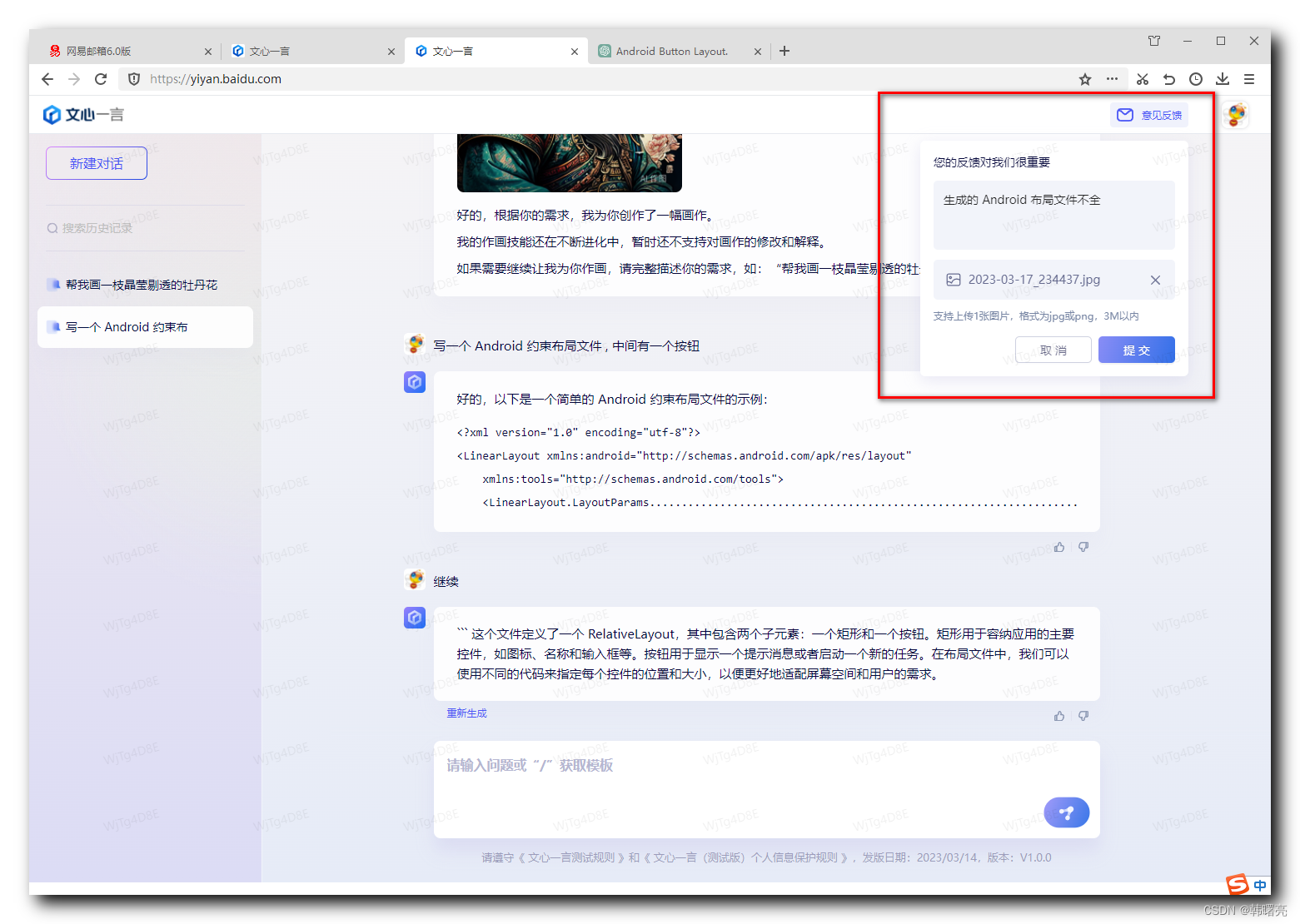
【AI 工具】文心一言内测记录
文章目录一、申请内测二、收到内测邀请三、激活内测四、开始使用1、普通对话2、生成图片3、生成代码4、写剧本5、生成小说五、问题反馈一、申请内测 到 https://yiyan.baidu.com/welcome 页面 , 点击 " 开始体验 " 按钮 , 申请试用 ; 申请时 , 需要填写相关信息 ; 主…...

Github的使用
Github Date: March 8, 2023 Sum: Github的使用 Github 了解开源相关的概念 1. 什么是开源 2. 什么是开源许可协议 开源并不意味着完全没有限制,为了限制使用者的使用范围和保护作者的权利,每个开源项目都应该遵守开源许可协议( Open Sou…...

抽丝剥茧还原真相,记一次神奇的崩溃
作者:靳倡荣 本文详细回放了一个崩溃案例的分析过程。回顾了C多态和类内存布局、pc指针与芯片异常处理、内存屏障的相关知识。 一、不讲“武德”的崩溃 1.1 查看崩溃调用栈 客户反馈了一个崩溃问题,并提供了core dump文件,查看崩溃调用栈如下…...

学习笔记八:docker资源配额
docker容器控制cpudocker容器控制cpu指定docker容器可以使用的cpu份额两个容器A、B的cpu份额分别为1000和500,结果会怎么样?给容器实例分配512权重的cpu使用份额总结CPU core核心控制扩展:服务器架构CPU配额控制参数的混合使用cpuset-cpus和c…...

小米10s格机修复 nv报错案例解析 关于基带分区的一些常识
前面分享过几期关于基带 diag端口与qcn相关的几篇帖子。其中一位粉丝朋友联系我。他的机型因为误格机导致手机进不去系统,反复进入官方rec报错nv损坏。进不去系统。 有兴趣的朋友可以参阅我的几个帖子,只是个人的一些片面理解。 基带相关贴; 安卓玩机…...
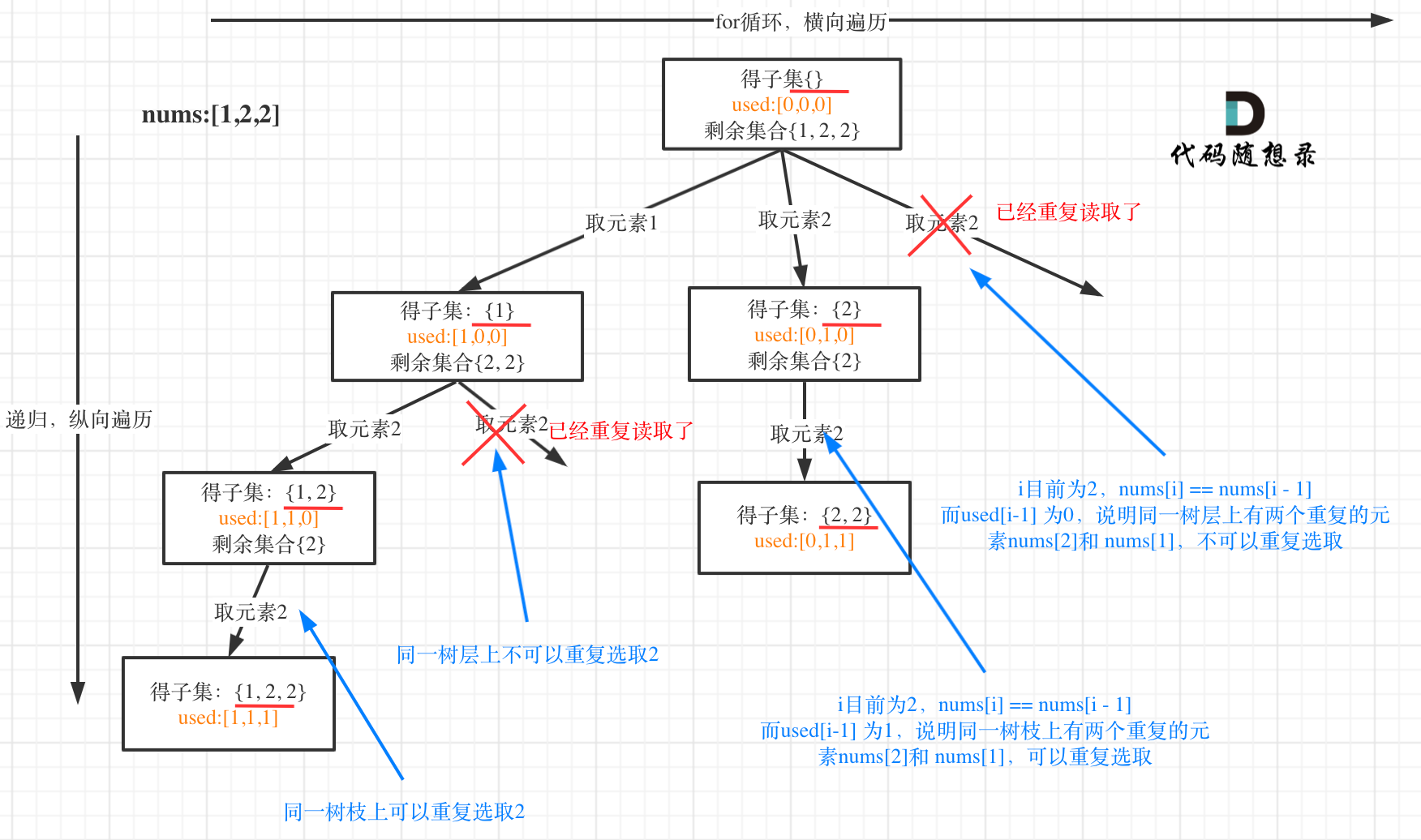
【3.17】MySQL索引整理、回溯(分割、子集问题)
3.1 索引常见面试题 索引的分类 什么是索引? 索引是一种数据结构,可以帮助MySQL快速定位到表中的数据。使用索引,可以大大提高查询的性能。 按「数据结构」分类:Btree索引、Hash索引、Full-text索引。 InnoDB 存储引擎创建的聚簇…...
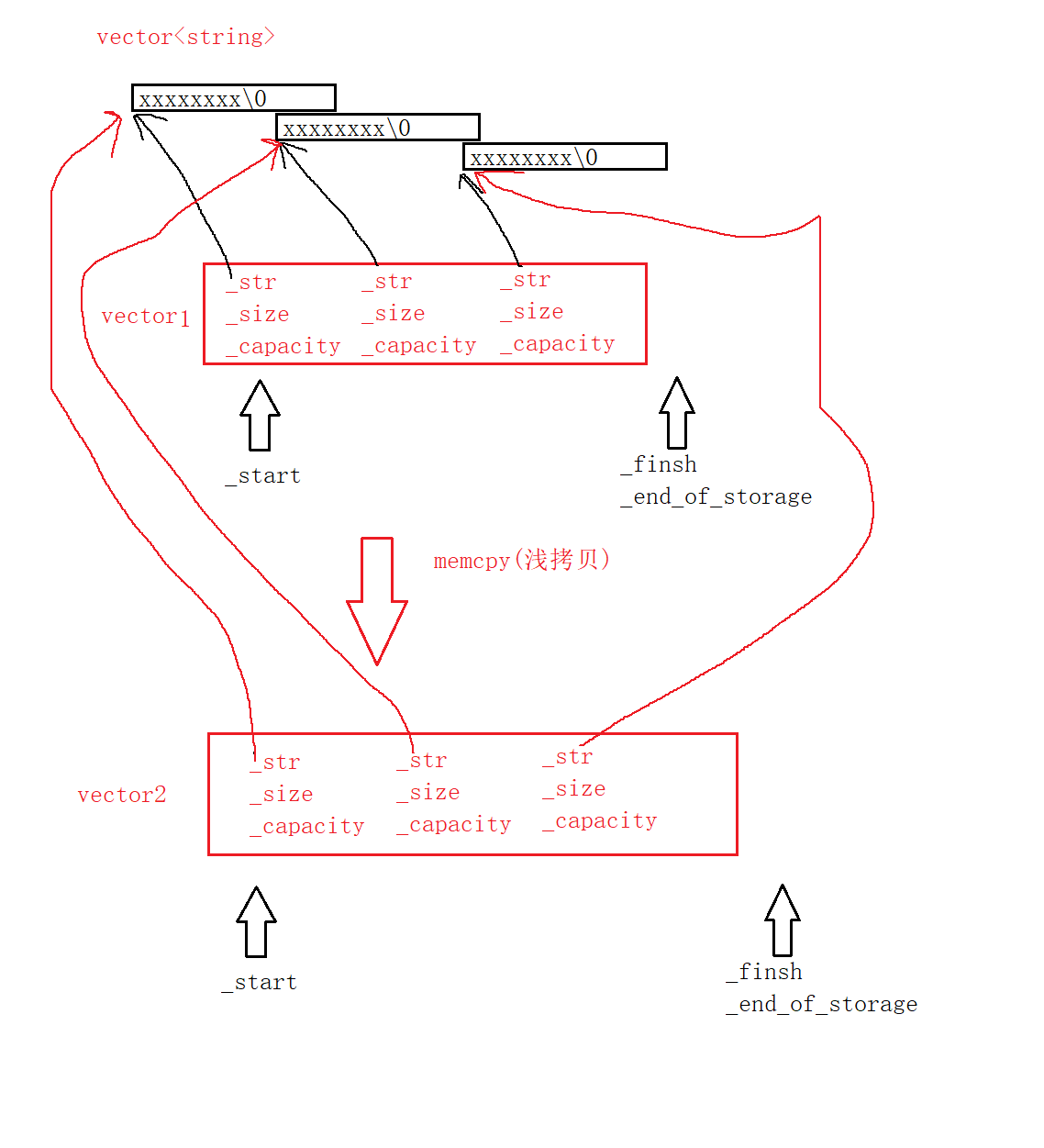
转解疑难杂症,详解vector迭代器失效和深浅拷贝的问题
前文http://t.csdn.cn/kVeVX——vector模拟实现本篇文章主要是针对vector中的两个比较经典的问题同时也是上一篇文章遗留下来的问题进行详细解释,第一个就是迭代器失效的问题,第二个是深浅拷贝的问题。ps:注意本文演示用的代码是上一篇vector…...
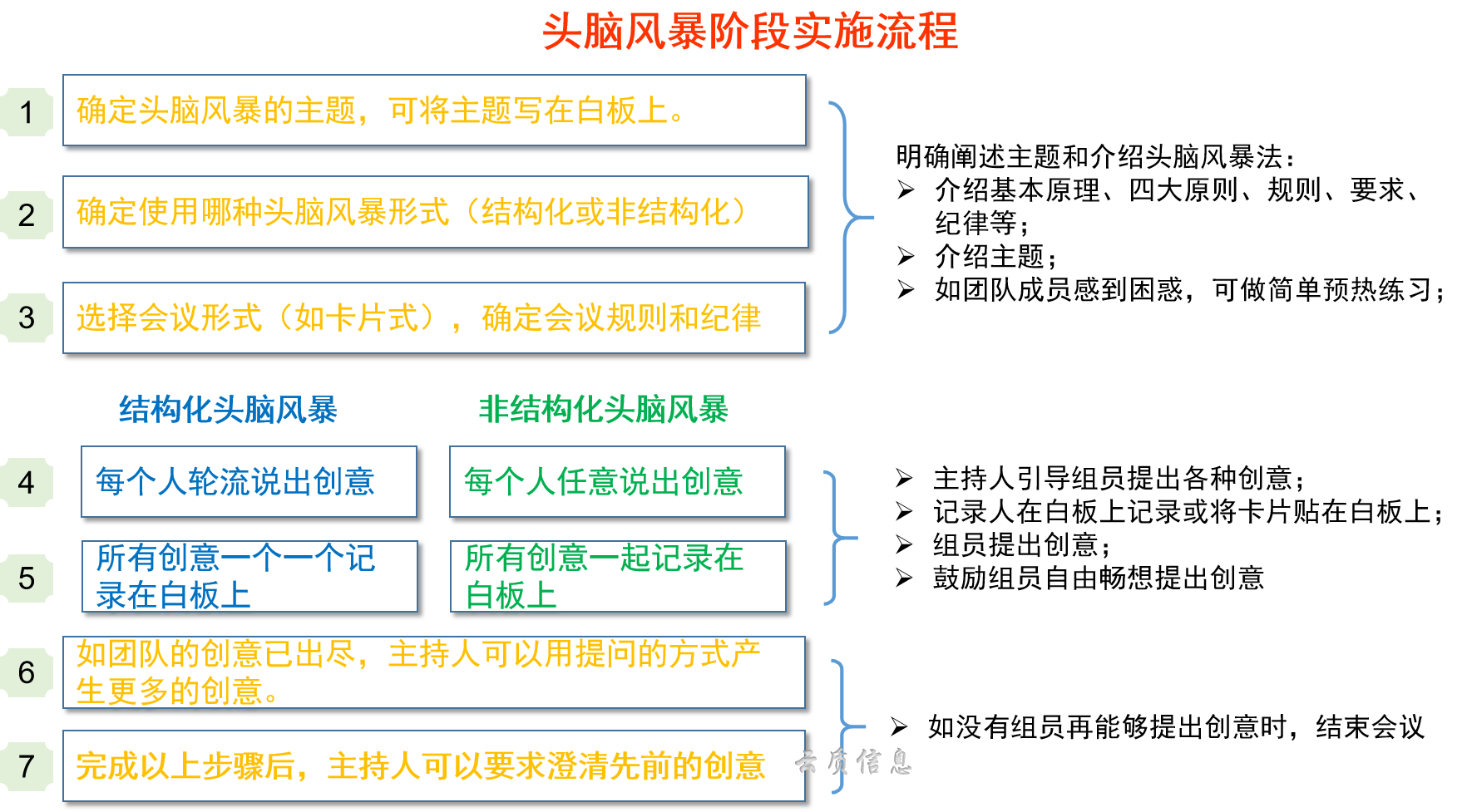
质量工具之头脑风暴法
云质QMS原创 转载请注明来源 作者:王洪石 1. 什么是头脑风暴法 头脑风暴最早是精神病理学上的用语,指的是精神病患者的精神错乱状态,后来拓展为无限制的自由联想和讨论,其目的在于产生新创意、激发新设想,或通过找到新…...

【3】核心易中期刊推荐——人工智能计算机仿真
🚀🚀🚀NEW!!!核心易中期刊推荐栏目来啦 ~ 📚🍀 核心期刊在国内的应用范围非常广,核心期刊发表论文是国内很多作者晋升的硬性要求,并且在国内属于顶尖论文发表,具有很高的学术价值。在中文核心目录体系中,权威代表有CSSCI、CSCD和北大核心。其中,中文期刊的数…...

vFlash软件简介
🍅 我是蚂蚁小兵,专注于车载诊断领域,尤其擅长于对CANoe工具的使用🍅 寻找组织 ,答疑解惑,摸鱼聊天,博客源码,点击加入👉【相亲相爱一家人】🍅 玩转CANoe&…...
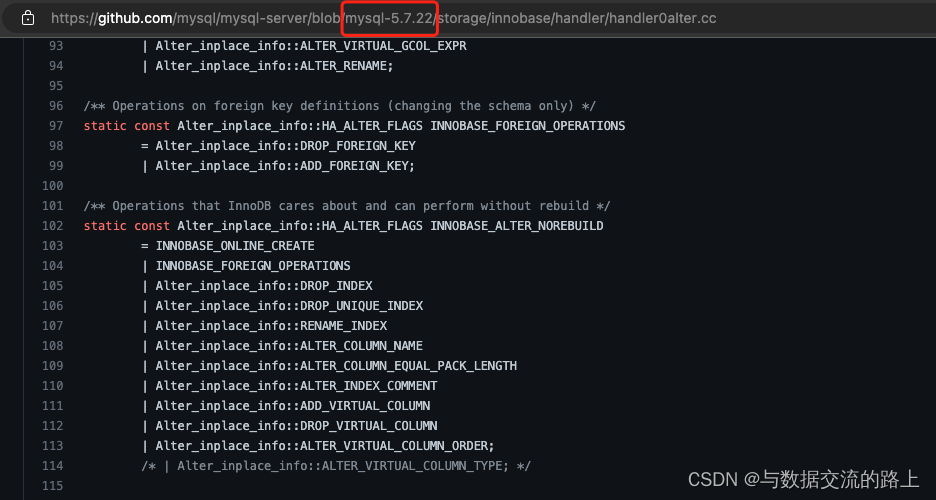
mysql-online-ddl是否需要rebuild
一、背景 DDL一直是DBA业务中的大项,看了TIDB的DDL讲解,恰巧我们的mysql业务大表也遇到了DDL的变更项,变更内容是将varchar(10)变更成varchar(20),这个变更通过官方文档很容易知道是不需要rebuild的(这里要注意下这个varchar(255…...

力扣-超过经理收入的员工
大家好,我是空空star,本篇带大家了解一道简单的力扣sql练习题。 文章目录前言一、题目:181. 超过经理收入的员工二、解题1.正确示范①提交SQL运行结果2.正确示范②提交SQL运行结果3.正确示范③提交SQL运行结果4.正确示范④提交SQL运行结果5.其…...
决策树基础知识点解读
目录 ID3算法 C4.5算法 CART树 ID3算法 定义:在决策树各个结点上应用信息增益准则选择特征,递归的构建决策树。该决策树是多分支分类。 信息增益 意义:给定特征X的条件下,使得类别Y的信息的不确定性减少的程度。取值越大越好。 定义&am…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...
