决策树基础知识点解读
目录
ID3算法
C4.5算法
CART树
ID3算法
定义:在决策树各个结点上应用信息增益准则选择特征,递归的构建决策树。该决策树是多分支分类。
信息增益
意义:给定特征X的条件下,使得类别Y的信息的不确定性减少的程度。取值越大越好。
定义:集合D的经验熵H(D)与特征A给定条件下D的经验条件熵H(D/A)之差。
缺点
- 分支过程中偏向取值较多的属性
- 无法处理连续值和缺失值,只能处理离散值
- 对缺失值敏感。
C4.5算法
定义:C4.5算法与ID3算法类似,C4.5算法使用信息增益比来选择特征。C4.5算法先从候选划分属性中找出信息增益高于平均水平的属性,再从中选择信息增益比最大的属性。该决策树是多分支分类。
信息增益比
定义:在信息增益的基础上,再除以H(D);取值越大越好。
连续属性的划分:采用"二分"法对连续属性进行离散化,划分点的选取可选使信息增益最大化的划分点。例:16个连续属性值选15个划分点。
缺点
- 分支过程中偏向取值较少的属性;
- 适合小样本
- 要进行剪枝操作;要对属性进行排序
CART树
CART树既可以用于分类,也可用于回归。CART树属于二叉树。
回归树
定义:使用平方误差来构建决策树,使用min(J){min(c1)sum(y-c1)^2+min(c2)sum(y-c2)^2}来选择最优划分变量和最优划分点。
预测:选择叶子节点的均值或者中位数作为当前节点的预测类别(通常都是均值)
分类树
定义:使用基尼系数选择最优特征。
基尼系数:
定义:从数据集中随机抽取两个样本,其类别标记不一致的概率。基尼系数越小,则样本集合的不确定性越小。
公式:1-sum(K){P(k)*P(k)},P(k)是属于第k个类别的概率,共有K个类别。
预测:选择叶子节点里概率最大的类别作为当前节点的预测类别;选择叶子节点中所有样本所属类别最多的那一类。
缺点:适合大样本
预剪枝:
过程:进行分支前,计算验证机准确率;分支后,计算验证机准确率,若变大,则进行分支,反之。
缺点:欠拟合风险较高。
后剪枝:
过程:当前决策树计算非叶子节点再验证集上的准确率,讲该非叶子节点替换为叶子节点后,计算验证机的准确率,若变大,则进行剪枝,反之。
决策树对缺失值的处理
- 删除缺失数据
- 用其他值猜测缺失项的可能值,如中位数、众数等,或者用已有数据构建模型,然后对缺失值进行预测
- 概率化:C4.5算法中,按比例对所有样本分配权重
- xgboost中,将缺失值分别导流到各个分支中,然后计算每个分支对损失函数的影响,该该缺失值分配到使得损失函数最小的分支。
树模型的优缺点
优点
- 可解释性强
- 可处理混合类型特征
- 不需要归一化
- 有特征组合、特征选择的作用
- 能够处理缺失值
- 对异常点鲁棒
- 可扩展性强,容易并行
缺点
- 却反平滑处理(回归预测的输出值只能输出若干种值)
- 不适合处理高维稀疏数据
树模型能够处理缺失值吗?(ID3、c4.5、cart、rf到底是如何处理缺失值的? - 知乎)
1.ID3不能处理
2.C4.5的处理方式:概率权重思想
- 特征值缺失,如何进行特征选择?用没有缺失的样本子集计算信息增益,再乘以权重(无缺失样本的比例),即为特征再数据集上的信息增益。
- 选定该划分特征,对于缺失该特征值的样本如何归类?将该缺失值同时划分到所有子节点种,并调整该缺失样本权重(该子节点在特征上取值的样本比例),即以不同概率将样本划分到所有节点种。
3.CART中可用surrogate splits(替代划分)来处理
- 特征值缺失,如何进行划分特征的选择?用没有缺失的样本子集来计算Gini指数(均方误差),再乘以一个权重(无缺失样本的比例),即为特征再数据集上的Gini指数(均方误差)
- 选定该划分特征,对于缺失该特征值的样本如何归类?首先,需要遍历剩余的特征,但是仅仅再完全没有缺失值的特征上进行选择,我们选择其中能够与目标缺失特征分裂之后效果最接近的特征值代替缺失值;如果不满足这个条件,缺失样本默认进入样本个数较多的叶节点。
对于sklearn库来说,是不能的,需要填充;而对于xgboost这种是可以的。
预测截断,遇到特征有缺失情况,如何处理?
样本默认分到右子树。
相关文章:
决策树基础知识点解读
目录 ID3算法 C4.5算法 CART树 ID3算法 定义:在决策树各个结点上应用信息增益准则选择特征,递归的构建决策树。该决策树是多分支分类。 信息增益 意义:给定特征X的条件下,使得类别Y的信息的不确定性减少的程度。取值越大越好。 定义&am…...

【C++】入门知识之 命名空间与输入输出
前言C语言是结构化和模块化的语言,适合处理较小规模的程序。对于复杂的问题,规模较大的程序,需要高度的抽象和建模时,C语言则不合适。为了解决软件危机, 20世纪80年代, 计算机界提出了OOP(object oriented …...

redis持久化的几种方式
一、简介 Redis是一种高级key-value数据库。它跟memcached类似,不过数据可以持久化,而且支持的数据类型很丰富。有字符串,链表,集 合和有序集合。支持在服务器端计算集合的并,交和补集(difference)等,还支持…...
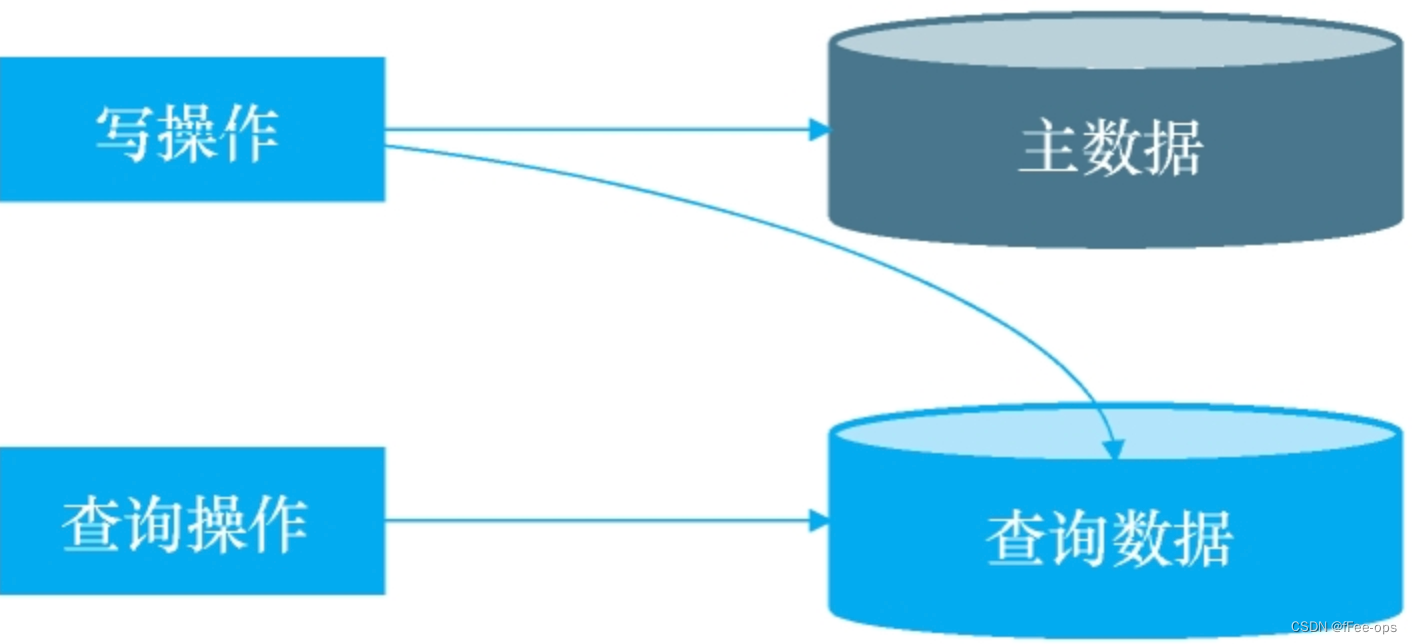
数据持久化层--查询分离
1. 业务场景 1)查询慢。当时工单数据库里面有1000万左右的客服工单时,每次查询时需要关联其他近10个表,一次查询平均花费13秒左右。 2)打开工单慢。工单打开以后需要调用多个接口,分别将用户信息、订单信息以及其他客服创建的单据信息列出来(如退款、赔偿、充值、投诉等…...

一文读懂Js中的this指向
前言 this关键字是一个非常重要的语法点。毫不夸张地说,不理解它的含义,大部分开发任务都无法完成。 简单说,this就是属性或方法“当前”所在的对象。 this.property上面代码中,this就代表property属性当前所在的对象。 下面是…...

零费用、零学习成本,用户快速可自定义json格式
随着物联网的发展,越来越多的设备被连接到互联网,数据量不断增加。这就需要有一种高效的方法来处理传输和处理这些数据。钡铼技术R40B边缘计算路由器,集成4G工业路由器、智能网关、RTU、DTU等产品多合一。支持边缘计算,它可以将计…...

2023年全国最新高校辅导员精选真题及答案25
百分百题库提供高校辅导员考试试题、辅导员考试预测题、高校辅导员考试真题、辅导员证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 101.属于大学教师职业特征的是()。 A.教师劳动的复杂性 B.教师…...

二、数据结构-线性表
目录 🌻🌻一、线性表概述1.1 线性表的基本概念1.2 线性表的顺序存储1.2.1 线性表的基本运算在顺序表上的实现1.2.2 顺序表实现算法的分析1.2.3 单链表类型的定义1.2.4 线性表的基本运算在单链表上的实现1.3 其他运算在单链表上的实现1.3.1 建表1.3.2 删除…...
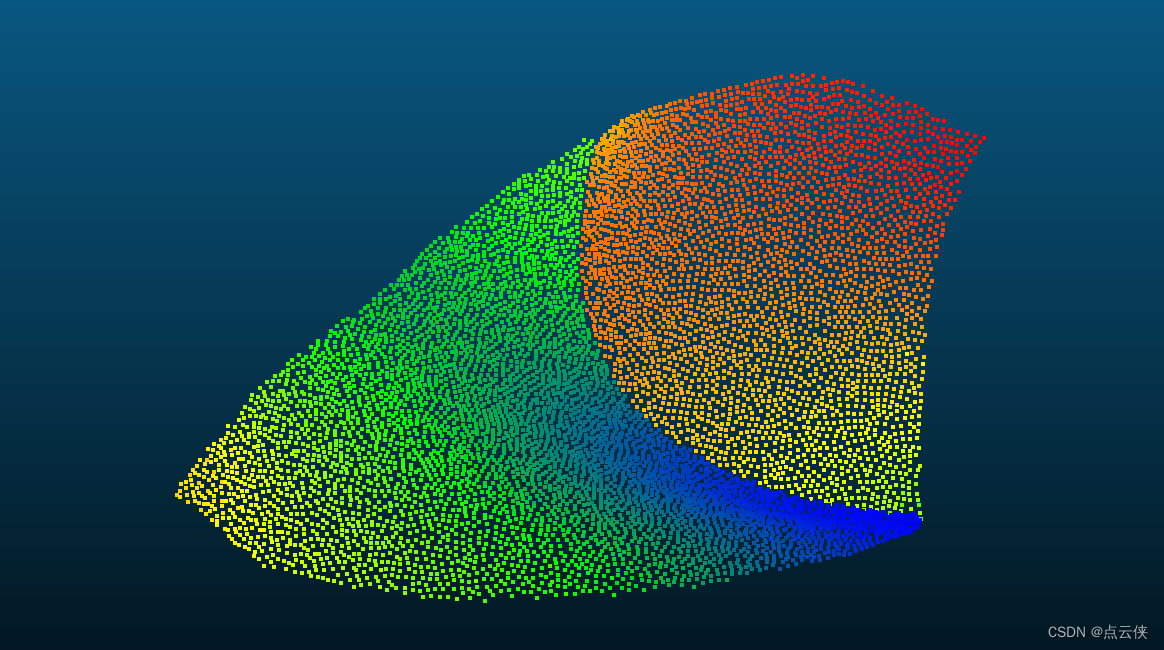
CGAL 点云上采样
目录一、算法原理1、主要函数2、参数解析二、代码实现三、结果展示一、算法原理 该方法对点集进行逐步上采样,同时根据法向量信息来检测边缘点,需要输入点云具有法线信息。在点云空洞填充和稀疏表面重建中具有较好的应用。 1、主要函数 头文件 #inclu…...
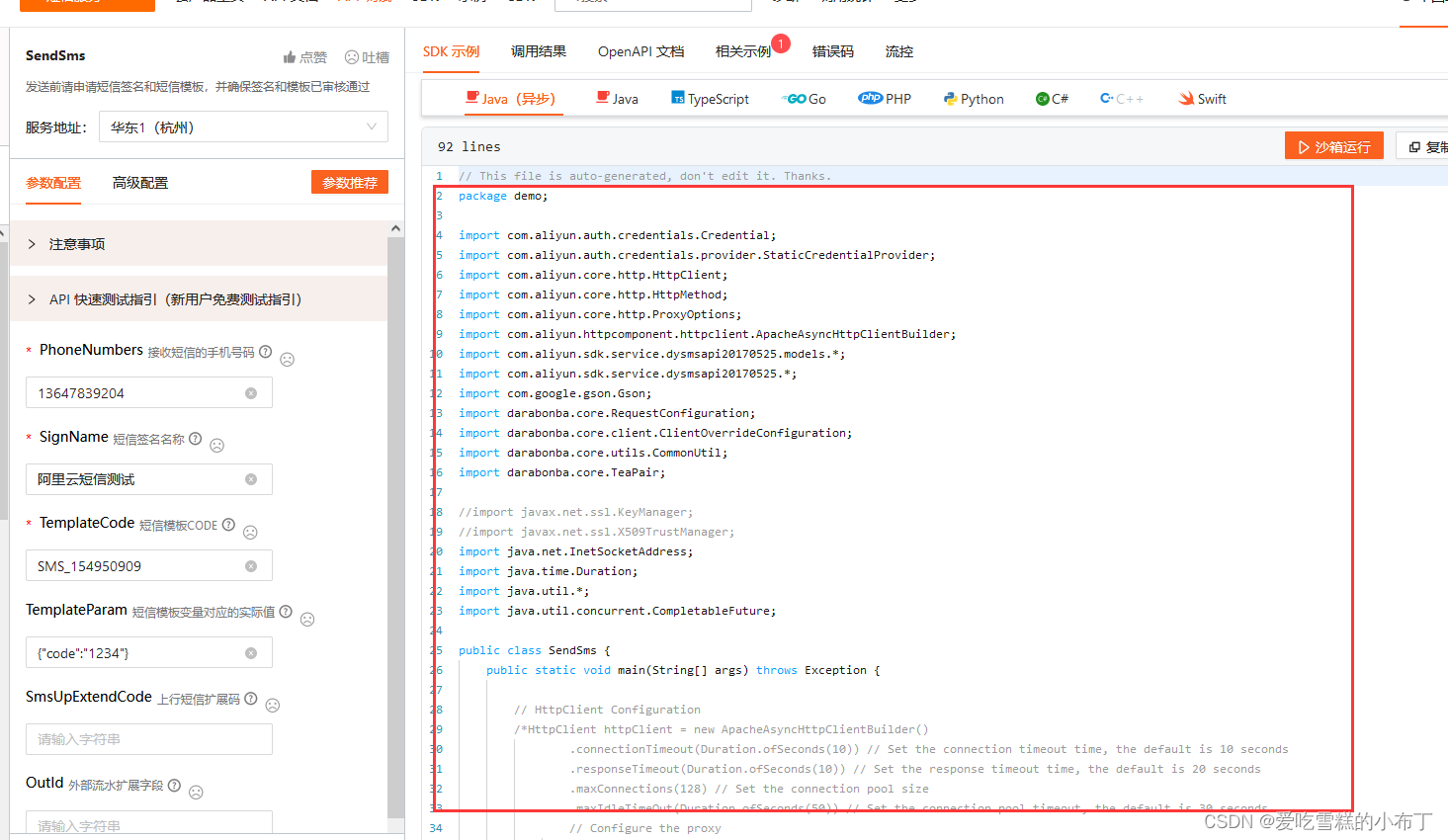
阿里云短信验证码实战
一、创建阿里云短信权限用户 1、登陆阿里云之后我们点击头像,接着点击AccessKey: 2、选择开始使用子用户 : 3、我们先要创建一个用户组: 4、依次点击新建的用户组——授权管理,给用户组授权,开通短信验证码服务…...

Android APP隐私合规检测工具Camille使用
目录一、简介二、环境准备常用使用方法一、简介 现如今APP隐私合规十分重要,各监管部门不断开展APP专项治理工作及核查通报,不合规的APP通知整改或直接下架。camille可以hook住Android敏感接口,检测是否第三方SDK调用。根据隐私合规的场景&a…...
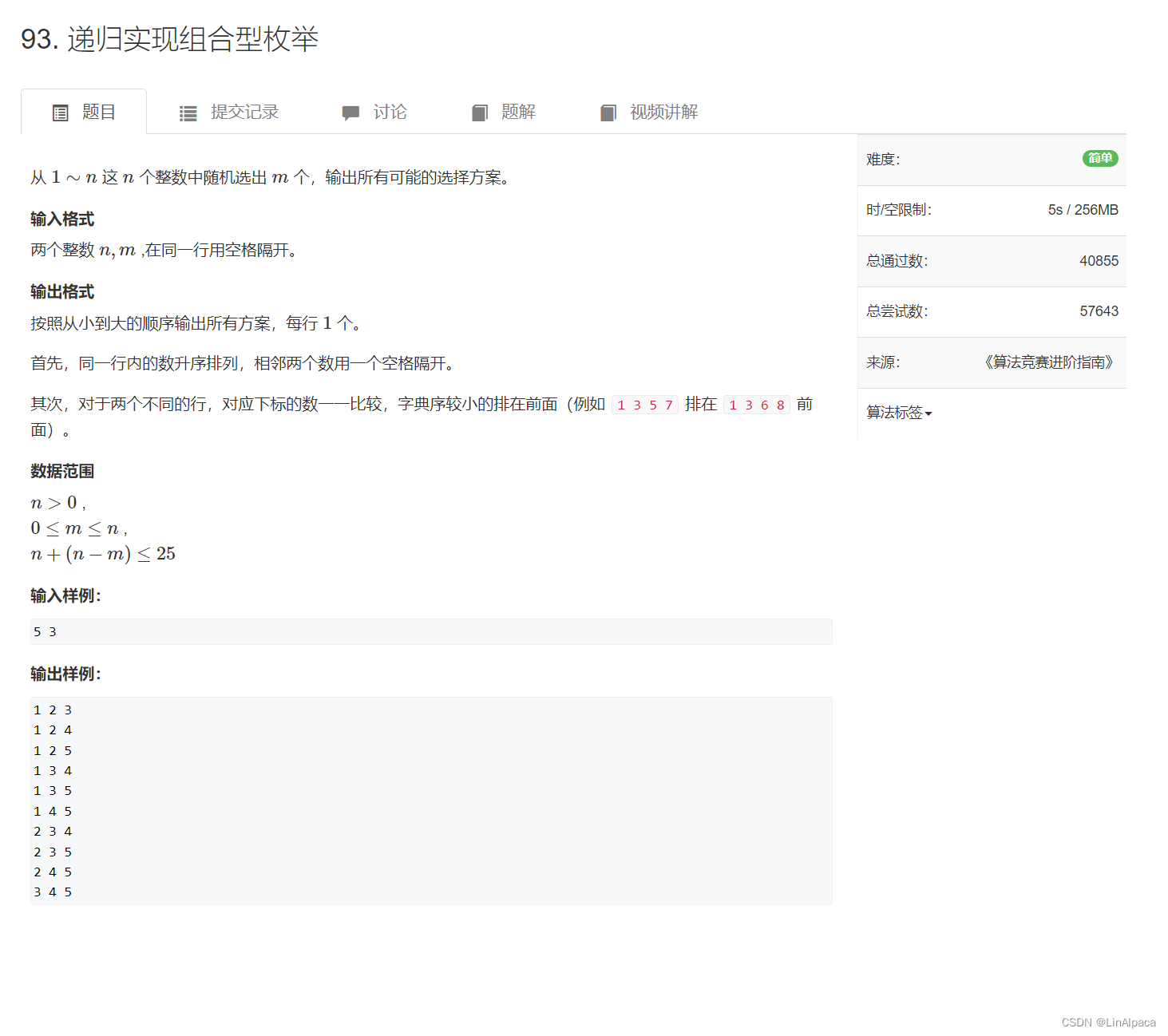
手把手学会DFS (递归入门)
目录 算法介绍 递归实现指数型枚举 递归实现排列型枚举 递归实现组合型枚举 算法介绍 🧩DFS 即 Depth First Search ,中文又叫深度优先搜索,是一种沿着树的深度对其进行遍历,直到尽头之后再进行回溯,再走其他路线的…...

由《三体》太阳文明末日场景想到的……
《三体》电视剧正在热播,热度持续不退,豆瓣评分8.6,基本已经预定年度口碑最高的科幻题材剧;除了在国内多个平台播出外,还走出国门,成功“出海”,《人民日报》两会特刊都予以了高度赞扬。 上图红…...

es6的Proxy与Reflect
Proxy是在对目标对象的读取时,架设一层拦截,可以在读取对象中的任意一个属性时做一些额外的操作 Proxy与Object.defineProperty方式设置setter、getter方法不同的是,Proxy是对目标对象的整体拦截,而Object.defineProperty注重对对…...
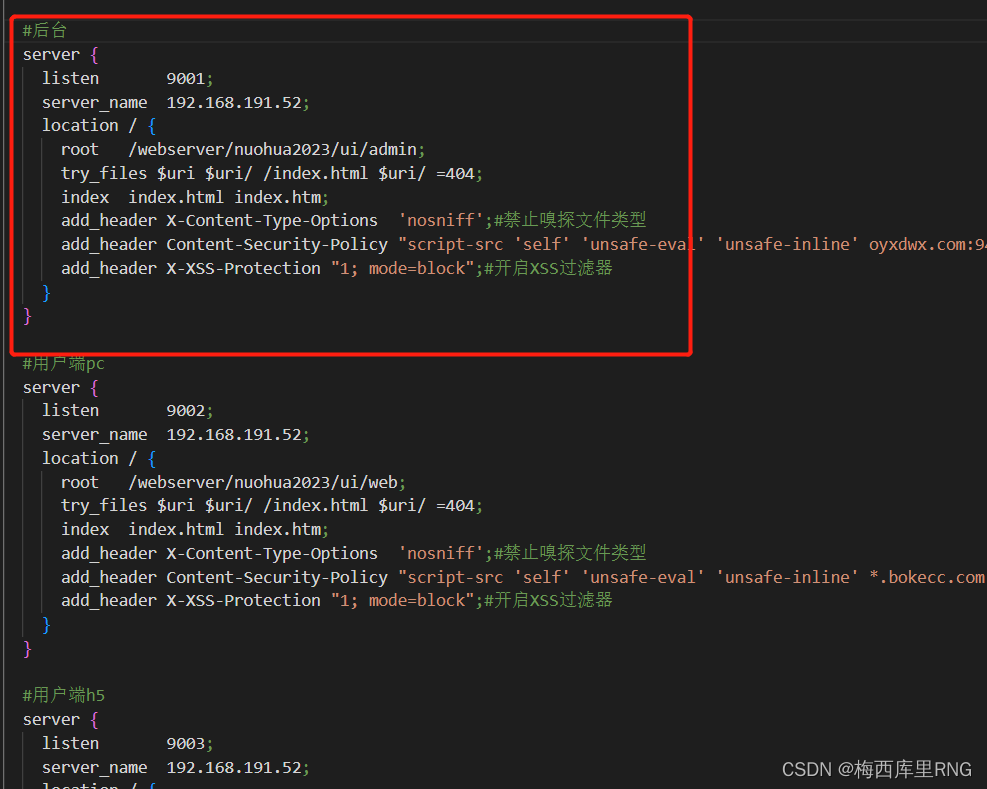
Linux环境部署vue项目 + nginx访问(包含nginx配置简介)
1、本地打包、上传 # 打包命令不同项目有略微差别,核心命令 npm run build# 我们项目前端给配了测试、生产环境,测试环境打包命令是 npm run build:stage# 建议先看一下项目的README文件打包之后,得到一个文件夹,一般叫dist、也有…...
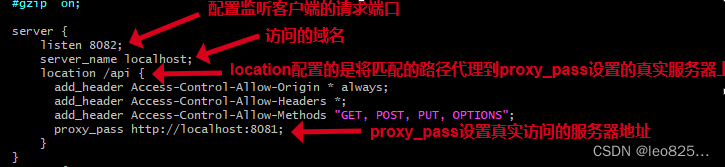
到底什么是跨域,如何解决跨域(常见的几种跨域解决方案)?
文章目录1、什么是跨域2、解决跨域的几种方案2.1、JSONP 方式解决跨域2.2、CORS 方式解决跨域(常见,通常仅需服务端修改即可)2.3、Nginx 反向代理解决跨域(推荐使用,配置简单)2.4、WebSocket 解决跨域2.5、…...
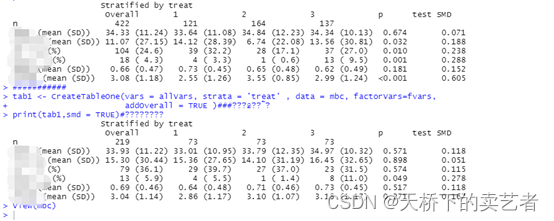
pm3包1.4版本发布----一个用于3组倾向性评分的R包
目前,本人写的第二个R包pm3包的1.4版本已经正式在CRAN上线,用于3组倾向评分匹配,只能3组不能多也不能少。 可以使用以下代码安装 install.packages("pm3")什么是倾向性评分匹配?倾向评分匹配(Propensity Sc…...

没有关系的话,那就去建立关系吧
今天给大家分享一道链表的好题--链表的深度拷贝,学会这道题,你的链表就可以达到优秀的水平了。力扣 先来理解一下题目意思,即建立一个新的单向链表,里面每个结点的值与对应的原链表相同,并且random指针也要指向新链表中…...
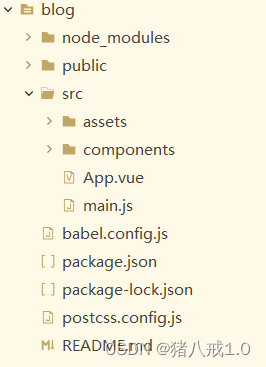
Vue项目
package.json : 描述这个NPM包的所有相关信息,包括作者、简介、包依赖、构建等信息,格式是严格的JSON格式。和java的maven的pom文件作用一样。 node_modules: 依赖需要下载后才能使用,存在依赖包的地方。使用npm install 安装依赖 babel.co…...
【webrtc】ICE 到VCMPacket的视频内存分配
ice的数据会在DataPacket 构造是进行内存分配和拷贝而后DataPacket 会传递给rtc模块处理rtc模块使用DataPacket 构造rtp包最终会给到OnReceivedPayloadData 进行rtp组帧。吊炸天的是DataPacket 竟然没有声明析构方法。RtpVideoStreamReceiver::OnReceivedPayloadData 的内存是外…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...
