【数学建模】——前沿图与网络模型:新时代算法解析与应用
目录
1.图与网络的基本概念
1. 无向图和有向图
2. 简单图、完全图、赋权图
3. 顶点的度
4. 子图与图的连通性
2.图的矩阵表示
1. 关联矩阵
2. 邻接矩阵
3.最短路问题
1.Dijkstra 算法
2.Floyd 算法
4.最小生成树问题
1.Kruskal 算法
2.Prim 算法
5.着色问题
6.旅行商问题
近似算法
7.网络最大流问题
Ford-Fulkerson 算法
8.计划评审方法与关键路径
9.钢管订购和运输
总结


专栏:数学建模学习笔记
上一篇:【MATLAB】和【Python】进行【图与网络模型】的高级应用与分析】
本篇是对上一篇的升华,进一步学习
1.图与网络的基本概念
1. 无向图和有向图
根据PPT内容,我们知道图的基本概念包括无向图和有向图。
- 无向图:边没有方向,表示为 (u, v) = (v, u)。
- 有向图:边有方向,表示为 (u, v) ≠ (v, u)。
PPT中的示例图可以用以下代码进行可视化:
import networkx as nx
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.font_manager import FontProperties# 设置中文字体
font = FontProperties(fname=r"C:\Windows\Fonts\simsun.ttc", size=15)# 无向图的邻接矩阵
A_undirected = np.array([[0, 1, 1, 0],[1, 0, 1, 1],[1, 1, 0, 1],[0, 1, 1, 0]
])# 有向图的邻接矩阵
A_directed = np.array([[0, 1, 0, 0],[0, 0, 1, 0],[0, 0, 0, 1],[1, 0, 0, 0]
])# 使用邻接矩阵创建无向图和有向图
G_undirected = nx.from_numpy_array(A_undirected)
G_directed = nx.from_numpy_array(A_directed, create_using=nx.DiGraph)# 绘制无向图
plt.figure(figsize=(10, 5))
plt.subplot(1, 2, 1)
nx.draw(G_undirected, with_labels=True, node_color='skyblue', edge_color='black', node_size=1500, font_size=20)
plt.title('无向图', fontproperties=font)# 绘制有向图
plt.subplot(1, 2, 2)
nx.draw(G_directed, with_labels=True, node_color='lightgreen', edge_color='red', node_size=1500, font_size=20, arrows=True)
plt.title('有向图', fontproperties=font)plt.show()

代码解析:
networkx库用于创建和操作图。matplotlib库用于绘图。nx.Graph()创建无向图,nx.DiGraph()创建有向图。add_edges_from()方法添加边。nx.draw()方法绘制图形。
2. 简单图、完全图、赋权图
- 简单图:没有自环和重边的图。
- 完全图:任意两个不同顶点之间都有边的图。
- 赋权图:边上有权值的图。
PPT中的示例图可以用以下代码进行可视化:
import networkx as nx
import matplotlib.pyplot as plt
# 简单图
G_simple = nx.Graph()
G_simple.add_edges_from([(1, 2), (2, 3), (3, 4), (4, 1)])
plt.figure(figsize=(8, 6))
plt.title("Simple Graph")
nx.draw(G_simple, with_labels=True, node_color='lightgreen', node_size=2000, edge_color='black', linewidths=1, font_size=15)
plt.show()# 完全图
G_complete = nx.complete_graph(5)
plt.figure(figsize=(8, 6))
plt.title("Complete Graph")
nx.draw(G_complete, with_labels=True, node_color='lightcoral', node_size=2000, edge_color='black', linewidths=1, font_size=15)
plt.show()# 赋权图
G_weighted = nx.Graph()
G_weighted.add_weighted_edges_from([(1, 2, 0.6), (1, 3, 0.2), (2, 3, 0.8), (2, 4, 0.4)])
plt.figure(figsize=(8, 6))
plt.title("Weighted Graph")
pos = nx.spring_layout(G_weighted)
nx.draw(G_weighted, pos, with_labels=True, node_color='lightblue', node_size=2000, edge_color='black', linewidths=1, font_size=15)
labels = nx.get_edge_attributes(G_weighted, 'weight')
nx.draw_networkx_edge_labels(G_weighted, pos, edge_labels=labels)
plt.show()



代码解析:
nx.complete_graph()创建完全图。nx.add_weighted_edges_from()添加有权值的边。nx.spring_layout()设置图的布局。nx.draw_networkx_edge_labels()显示边的权值。
3. 顶点的度
- 顶点的度:连接该顶点的边的数目。
PPT中的示例可以用以下代码展示顶点的度:
import networkx as nx
import matplotlib.pyplot as plt# 计算无向图的顶点度
G_undirected = nx.Graph()
G_undirected.add_edges_from([(1, 2), (1, 3), (2, 4), (3, 4)])
G_undirected_degree = G_undirected.degree()
plt.figure(figsize=(8, 6))
plt.title("Undirected Graph - Node Degree")
nx.draw(G_undirected, with_labels=True, node_color='skyblue', node_size=[v * 1000 for k, v in G_undirected_degree], edge_color='black', linewidths=1, font_size=15)
plt.show()# 计算有向图的顶点入度和出度
G_directed = nx.DiGraph()
G_directed.add_edges_from([(1, 2), (1, 3), (2, 4), (3, 4)])
G_directed_in_degree = G_directed.in_degree()
G_directed_out_degree = G_directed.out_degree()
plt.figure(figsize=(8, 6))
plt.title("Directed Graph - Node In-Degree")
nx.draw(G_directed, with_labels=True, node_color='skyblue', node_size=[v * 1000 for k, v in G_directed_in_degree], edge_color='black', arrows=True, linewidths=1, font_size=15)
plt.show()plt.figure(figsize=(8, 6))
plt.title("Directed Graph - Node Out-Degree")
nx.draw(G_directed, with_labels=True, node_color='skyblue', node_size=[v * 1000 for k, v in G_directed_out_degree], edge_color='black', arrows=True, linewidths=1, font_size=15)
plt.show()
代码解析:
degree()计算无向图顶点的度。in_degree()计算有向图顶点的入度。out_degree()计算有向图顶点的出度。



4. 子图与图的连通性
- 子图:原图的部分顶点和边组成的图。
- 连通图:任意两个顶点之间都有路径相连的图。
PPT中的示例可以用以下代码展示子图和连通性:
import networkx as nx
import matplotlib.pyplot as plt# 子图示例
G_undirected = nx.Graph()
G_undirected.add_edges_from([(1, 2), (1, 3), (2, 4), (3, 4)])
subgraph_nodes = [1, 2, 3]
G_subgraph = G_undirected.subgraph(subgraph_nodes)
plt.figure(figsize=(8, 6))
plt.title("Subgraph")
nx.draw(G_subgraph, with_labels=True, node_color='yellow', node_size=2000, edge_color='black', linewidths=1, font_size=15)
plt.show()# 连通图示例
G_connected = nx.cycle_graph(5)
plt.figure(figsize=(8, 6))
plt.title("Connected Graph")
nx.draw(G_connected, with_labels=True, node_color='lightblue', node_size=2000, edge_color='black', linewidths=1, font_size=15)
plt.show()# 不连通图示例
G_disconnected = nx.Graph()
G_disconnected.add_edges_from([(1, 2), (3, 4)])
plt.figure(figsize=(8, 6))
plt.title("Disconnected Graph")
nx.draw(G_disconnected, with_labels=True, node_color='lightblue', node_size=2000, edge_color='black', linewidths=1, font_size=15)
plt.show()
代码解析:
subgraph()生成子图。cycle_graph()创建连通图(环图)。- 添加孤立的边以生成不连通图。



2.图的矩阵表示
1. 关联矩阵
关联矩阵用于表示图中顶点与边之间的关系。在无向图中,关联矩阵是一个 |V| × |E| 的矩阵,其中 |V| 是顶点数,|E| 是边数。矩阵中的元素 a[i][j] 表示顶点 i 是否与边 j 相连,如果相连则为 1,否则为 0。在有向图中,a[i][j] 为 -1 表示顶点 i 是边 j 的起点,为 1 表示顶点 i 是边 j 的终点。
根据PPT的描述,我们可以用以下代码展示关联矩阵:
import networkx as nx
import numpy as np# 无向图
G_undirected = nx.Graph()
G_undirected.add_edges_from([(1, 2), (1, 3), (2, 4), (3, 4)])
G_undirected_adj = nx.incidence_matrix(G_undirected).todense()
print("无向图的关联矩阵:\n", G_undirected_adj)# 有向图
G_directed = nx.DiGraph()
G_directed.add_edges_from([(1, 2), (1, 3), (2, 4), (3, 4)])
G_directed_adj = nx.incidence_matrix(G_directed, oriented=True).todense()
print("有向图的关联矩阵:\n", G_directed_adj)
代码解析:
incidence_matrix()计算关联矩阵。oriented=True用于有向图。
无向图的关联矩阵:[[1. 1. 0. 0.][1. 0. 1. 0.][0. 1. 0. 1.][0. 0. 1. 1.]]
有向图的关联矩阵:[[-1. -1. 0. 0.][ 1. 0. -1. 0.][ 0. 1. 0. -1.][ 0. 0. 1. 1.]]
2. 邻接矩阵
邻接矩阵用于表示顶点之间是否直接相连。对于一个有 n 个顶点的图,邻接矩阵是一个 n × n 的矩阵。对于无向图,如果顶点 i 与顶点 j 之间有边相连,则 a[i][j] = 1,否则 a[i][j] = 0。在赋权图中,a[i][j] 表示顶点 i 和顶点 j 之间边的权值,如果没有边则为 0 或无穷大。
根据PPT的描述,我们可以用以下代码展示邻接矩阵:
import networkx as nx# 无向图
G_undirected = nx.Graph()
G_undirected.add_edges_from([(1, 2), (1, 3), (2, 4), (3, 4)])
G_undirected_adj_matrix = nx.adjacency_matrix(G_undirected).todense()
print("无向图的邻接矩阵:\n", G_undirected_adj_matrix)# 有向图
G_directed = nx.DiGraph()
G_directed.add_edges_from([(1, 2), (1, 3), (2, 4), (3, 4)])
G_directed_adj_matrix = nx.adjacency_matrix(G_directed).todense()
print("有向图的邻接矩阵:\n", G_directed_adj_matrix)
代码解析:
adjacency_matrix()计算邻接矩阵。
无向图的邻接矩阵:[[0 1 1 0][1 0 0 1][1 0 0 1][0 1 1 0]]
有向图的邻接矩阵:[[0 1 1 0][0 0 0 1][0 0 0 1][0 0 0 0]]
3.最短路问题
最短路问题是指在赋权图中,找到从源点到目标点的最短路径。常见的算法有 Dijkstra 算法和 Floyd 算法。
1.Dijkstra 算法
Dijkstra 算法用于求解单源最短路径问题,适用于所有边权值为非负的图。算法的基本思想是通过贪心策略,每次选择距离起点最近的未访问顶点,并更新其邻接顶点的距离。具体步骤如下:
- 初始化源点到自身的距离为 0,其余顶点的距离为无穷大。
- 将所有顶点加入未访问集合。
- 从未访问集合中选择距离起点最近的顶点 u,标记 u 为已访问。
- 对于 u 的每个邻接顶点 v,如果 u 到 v 的距离加上 u 到起点的距离小于 v 到起点的当前距离,则更新 v 的距离。
- 重复步骤 3 和 4,直到所有顶点都被访问。
Dijkstra 算法的时间复杂度为 O(V^2),对于稠密图比较适用。如果使用优先队列进行优化,时间复杂度可以降到 O(E log V)。
PPT中的示例可以用以下代码展示Dijkstra算法:
import heapqdef dijkstra(graph, start):pq = [(0, start)]distances = {vertex: float('infinity') for vertex in graph}distances[start] = 0while pq:current_distance, current_vertex = heapq.heappop(pq)if current_distance > distances[current_vertex]:continuefor neighbor, weight in graph[current_vertex].items():distance = current_distance + weightif distance < distances[neighbor]:distances[neighbor] = distanceheapq.heappush(pq, (distance, neighbor))return distancesgraph = {'A': {'B': 1, 'C': 4},'B': {'A': 1, 'C': 2, 'D': 5},'C': {'A': 4, 'B': 2, 'D': 1},'D': {'B': 5, 'C': 1}
}distances = dijkstra(graph, 'A')
print("Dijkstra's Algorithm Output:", distances)
代码解析:
heapq用于实现优先队列。dijkstra()函数实现了Dijkstra算法。distances存储每个顶点的最短距离。
Dijkstra's Algorithm Output: {'A': 0, 'B': 1, 'C': 3, 'D': 4}
2.Floyd 算法
Floyd 算法用于求解任意两点间的最短路径问题,适用于所有边权值为非负的图。算法的基本思想是通过动态规划,每次考虑加入一个中间顶点来更新最短路径。具体步骤如下:
- 初始化一个距离矩阵,直接使用图的邻接矩阵表示顶点之间的距离。
- 对于每个顶点 k,更新所有顶点对 (i, j) 的距离。如果 i 到 j 的距离通过顶点 k 更短,则更新距离矩阵。
- 重复上述步骤,直到考虑完所有顶点。
Floyd 算法的时间复杂度为 O(V^3),适用于稀疏图和需要频繁查询任意两点最短路径的情况。
PPT中的示例可以用以下代码展示Floyd算法:
def floyd_warshall(graph):nodes = list(graph.keys())distances = {node: {node2: float('infinity') for node2 in nodes} for node in nodes}for node in nodes:distances[node][node] = 0for node in graph:for neighbor in graph[node]:distances[node][neighbor] = graph[node][neighbor]for k in nodes:for i in nodes:for j in nodes:if distances[i][j] > distances[i][k] + distances[k][j]:distances[i][j] = distances[i][k] + distances[k][j]return distancesgraph = {'A': {'B': 1, 'C': 4},'B': {'A': 1, 'C': 2, 'D': 5},'C': {'A': 4, 'B': 2, 'D': 1},'D': {'B': 5, 'C': 1}
}distances = floyd_warshall(graph)
print("Floyd-Warshall Algorithm Output:")
for row in distances:print(row, distances[row])
代码解析:
floyd_warshall()函数实现了Floyd算法。distances存储每对顶点之间的最短距离。
Floyd-Warshall Algorithm Output:
A {'A': 0, 'B': 1, 'C': 3, 'D': 4}
B {'A': 1, 'B': 0, 'C': 2, 'D': 3}
C {'A': 3, 'B': 2, 'C': 0, 'D': 1}
D {'A': 4, 'B': 3, 'C': 1, 'D': 0}
4.最小生成树问题
最小生成树问题是指在一个连通图中,找到一棵包含所有顶点且边权值之和最小的树。常见的算法有 Kruskal 算法和 Prim 算法。
1.Kruskal 算法
Kruskal 算法是一种贪心算法,主要思想是每次选择权值最小的边,并保证不形成圈,直到构建出最小生成树。具体步骤如下:
- 将图中的所有边按权值从小到大排序。
- 初始化一个空集合,用于存放最小生成树的边。
- 从权值最小的边开始,依次选择边,如果选择的边与当前集合中的边不形成圈,则将该边加入集合。
- 重复步骤 3,直到集合中包含 n-1 条边,其中 n 是图的顶点数。
Kruskal 算法的时间复杂度为 O(E log E),适用于边数较少的稀疏图。
PPT中的示例可以用以下代码展示Kruskal算法:
class DisjointSet:def __init__(self, vertices):self.parent = {v: v for v in vertices}self.rank = {v: 0 for v in vertices}def find(self, item):if self.parent[item] != item:self.parent[item] = self.find(self.parent[item])return self.parent[item]def union(self, set1, set2):root1 = self.find(set1)root2 = self.find(set2)if root1 != root2:if self.rank[root1] > self.rank[root2]:self.parent[root2] = root1else:self.parent[root1] = root2if self.rank[root1] == self.rank[root2]:self.rank[root2] += 1def kruskal(graph):edges = [(weight, u, v) for u in graph for v, weight in graph[u].items()]edges.sort()ds = DisjointSet(graph.keys())mst = []for edge in edges:weight, u, v = edgeif ds.find(u) != ds.find(v):ds.union(u, v)mst.append((u, v, weight))return mstgraph = {'A': {'B': 1, 'C': 4},'B': {'A': 1, 'C': 2, 'D': 5},'C': {'A': 4, 'B': 2, 'D': 1},'D': {'B': 5, 'C': 1}
}mst = kruskal(graph)
print("Kruskal's Algorithm Output:", mst)
代码解析:
DisjointSet类用于实现并查集,以检测是否形成环。kruskal()函数实现了Kruskal算法。edges存储图中的所有边并按权值排序。mst存储最小生成树的边。
Kruskal's Algorithm Output: [('A', 'B', 1), ('C', 'D', 1), ('B', 'C', 2)]
2.Prim 算法
Prim 算法也是一种贪心算法,主要思想是从一个顶点开始,每次选择连接已选顶点集合和未选顶点集合的最小权值边,直至所有顶点都被选中。具体步骤如下:
- 初始化一个顶点集合,包括图中的任意一个顶点。
- 初始化一个空集合,用于存放最小生成树的边。
- 从顶点集合中选择一条连接已选顶点和未选顶点的最小权值边,将该边和边的终点加入集合。
- 重复步骤 3,直到所有顶点都被选中。
Prim 算法的时间复杂度为 O(V^2),适用于顶点数较少的稠密图。如果使用优先队列进行优化,时间复杂度可以降到 O(E log V)。
PPT中的示例可以用以下代码展示Prim算法:
import heapqdef prim(graph, start):mst = []visited = {start}edges = [(weight, start, to) for to, weight in graph[start].items()]heapq.heapify(edges)while edges:weight, frm, to = heapq.heappop(edges)if to not in visited:visited.add(to)mst.append((frm, to, weight))for to_next, weight in graph[to].items():if to_next not in visited:heapq.heappush(edges, (weight, to, to_next))return mstgraph = {'A': {'B': 1, 'C': 4},'B': {'A': 1, 'C': 2, 'D': 5},'C': {'A': 4, 'B': 2, 'D': 1},'D': {'B': 5, 'C': 1}
}mst = prim(graph, 'A')
print("Prim's Algorithm Output:", mst)
代码解析:
prim()函数实现了Prim算法。visited存储已选顶点。edges存储连接已选顶点和未选顶点的边。
Prim's Algorithm Output: [('A', 'B', 1), ('B', 'C', 2), ('C', 'D', 1)]
5.着色问题
图着色是指将图的顶点涂上不同的颜色,使得相邻顶点颜色不同。图着色问题的目的是使用尽可能少的颜色。图着色在调度问题、地图着色等实际问题中有广泛应用。
PPT中的示例可以用以下代码展示图着色:
import networkx as nx
import matplotlib.pyplot as pltdef greedy_coloring(graph):color_map = {}for node in graph:available_colors = set(range(len(graph)))for neighbor in graph[node]:if neighbor in color_map:available_colors.discard(color_map[neighbor])color_map[node] = min(available_colors)return color_mapgraph = {'A': ['B', 'C'],'B': ['A', 'C', 'D'],'C': ['A', 'B', 'D'],'D': ['B', 'C']
}coloring = greedy_coloring(graph)
print("Graph Coloring Output:", coloring)# 可视化图着色
G_coloring = nx.Graph(graph)
colors = [coloring[node] for node in G_coloring.nodes()]
plt.figure(figsize=(8, 6))
plt.title("Graph Coloring")
nx.draw(G_coloring, with_labels=True, node_color=colors, node_size=2000, cmap=plt.cm.rainbow, edge_color='black', linewidths=1, font_size=15)
plt.show()
代码解析:
greedy_coloring()函数实现了贪心着色算法。color_map存储每个顶点的颜色。available_colors存储每个顶点可用的颜色。
Graph Coloring Output: {'A': 0, 'B': 1, 'C': 2, 'D': 0}

6.旅行商问题
旅行商问题是指在一组城市中找出一条最短路径,使得旅行商访问每个城市一次并回到起点。这是一个经典的 NP 完全问题,求解方法包括近似算法和启发式算法。
近似算法
由于旅行商问题的复杂性,通常使用近似算法来求解,如贪心算法、动态规划等。贪心算法通过每次选择距离当前城市最近的未访问城市来构建路径,而动态规划通过记忆化搜索来避免重复计算。
PPT中的示例可以用以下代码展示旅行商问题:
import itertoolsdef tsp_brute_force(graph):nodes = list(graph.keys())shortest_path = Nonemin_cost = float('infinity')for perm in itertools.permutations(nodes):cost = 0for i in range(len(perm) - 1):cost += graph[perm[i]][perm[i + 1]]cost += graph[perm[-1]][perm[0]]if cost < min_cost:min_cost = costshortest_path = permreturn shortest_path, min_costgraph = {'A': {'B': 10, 'C': 15, 'D': 20},'B': {'A': 10, 'C': 35, 'D': 25},'C': {'A': 15, 'B': 35, 'D': 30},'D': {'A': 20, 'B': 25, 'C': 30}
}path, cost = tsp_brute_force(graph)
print("TSP Brute Force Output:", path, "with cost", cost)
代码解析:
itertools.permutations()生成所有可能的路径。tsp_brute_force()函数实现了暴力求解旅行商问题。shortest_path存储最短路径,min_cost存储最小成本。
TSP Brute Force Output: ('A', 'B', 'D', 'C') with cost 80
7.网络最大流问题
网络最大流问题是指在一个流网络中,找到从源点到汇点的最大流量路径。常见的算法有 Ford-Fulkerson 算法。
Ford-Fulkerson 算法
Ford-Fulkerson 算法通过反复寻找增广路径来增加流量,直到找不到增广路径为止。具体步骤如下:
- 初始化流量为 0。
- 使用深度优先搜索或广度优先搜索找到一条增广路径。
- 更新增广路径上的流量,增加路径上的最小残余容量。
- 重复步骤 2 和 3,直到找不到增广路径。
Ford-Fulkerson 算法的时间复杂度为 O(E |f|),其中 E 是边数,|f| 是最大流量的值。
PPT中的示例可以用以下代码展示Ford-Fulkerson算法:
from collections import dequedef bfs(C, F, source, sink):queue = deque([source])paths = {source: []}while queue:u = queue.popleft()for v in C[u]:if C[u][v] - F[u][v] > 0 and v not in paths:paths[v] = paths[u] + [(u, v)]if v == sink:return paths[v]queue.append(v)return Nonedef ford_fulkerson(graph, source, sink):C = {u: {} for u in graph}for u in graph:for v, capacity in graph[u].items():C[u][v] = capacityif v not in C:C[v] = {}C[v][u] = 0F = {u: {v: 0 for v in C[u]} for u in C}max_flow = 0while True:path = bfs(C, F, source, sink)if not path:breakflow = min(C[u][v] - F[u][v] for u, v in path)for u, v in path:F[u][v] += flowF[v][u] -= flowmax_flow += flowreturn max_flowgraph = {'A': {'B': 3, 'C': 3},'B': {'C': 2, 'D': 3},'C': {'D': 2, 'E': 2},'D': {'F': 2},'E': {'D': 1, 'F': 3},'F': {}
}max_flow = ford_fulkerson(graph, 'A', 'F')
print("Ford-Fulkerson Algorithm Output:", max_flow)
代码解析:
bfs()函数实现广度优先搜索,找到增广路径。ford_fulkerson()函数实现Ford-Fulkerson算法。C存储容量,F存储流量。max_flow存储最大流量。
Ford-Fulkerson Algorithm Output: 4
8.计划评审方法与关键路径
关键路径法(CPM)用于项目管理中,通过计算项目中各任务的最早开始时间和最晚完成时间,找出影响项目工期的关键路径。关键路径是指项目中耗时最长的路径,决定了项目的最短完成时间。
PPT中的示例可以用以下代码展示关键路径法:
def critical_path_method(tasks):longest_path = []max_duration = 0for task in tasks:if task['duration'] > max_duration:max_duration = task['duration']longest_path = [task['name']]elif task['duration'] == max_duration:longest_path.append(task['name'])return longest_path, max_durationtasks = [{'name': 'A', 'duration': 3},{'name': 'B', 'duration': 2},{'name': 'C', 'duration': 4},{'name': 'D', 'duration': 1},{'name': 'E', 'duration': 3}
]path, duration = critical_path_method(tasks)
print("Critical Path Method Output:", path, "with duration", duration)
代码解析:
critical_path_method()函数计算关键路径。tasks存储每个任务的名称和持续时间。longest_path存储关键路径,max_duration存储最长持续时间。
Critical Path Method Output: ['C'] with duration 4
9.钢管订购和运输
钢管订购和运输问题涉及从多个供应点向需求点运输钢管,要求最小化运输和铺设费用。具体步骤包括:
- 构建运费矩阵,计算从各个供应点到各个需求点的运输费用。
- 构建数学规划模型,设定目标函数为总费用最小化。
- 使用优化算法求解模型,确定最佳的订购和运输方案。
PPT中的示例可以用以下代码展示钢管订购和运输问题:
from scipy.optimize import linprogc = [20, 30, 10, 40, 30, 20, 10, 20, 10] # 费用系数
A_eq = [[1, 1, 0, 1, 0, 0, 0, 0, 0],[0, 0, 1, 0, 1, 1, 0, 0, 0],[0, 0, 0, 0, 0, 0, 1, 1, 1]
] # 约束条件
b_eq = [200, 150, 100] # 需求
bounds = [(0, float('inf'))] * len(c) # 变量边界res = linprog(c, A_eq=A_eq, b_eq=b_eq, bounds=bounds, method='highs')
print("Optimal value:", res.fun)
print("Optimal solution:", res.x)
代码解析:
linprog()函数求解线性规划问题。c表示费用系数,A_eq表示约束条件,b_eq表示需求,bounds表示变量边界。res.fun返回最优值,res.x返回最优解。
Optimal value: 6500.0
Optimal solution: [200. 0. 150. 0. 0. 0. 100. 0. 0.]
总结
图与网络模型的基本概念、矩阵表示、最短路径、最小生成树、着色问题、旅行商问题、网络最大流问题及关键路径法等主题,结合PPT内容和Python代码实例,深入解析了每个主题的核心算法和应用场景,提供了可视化代码和图形展示,以便更好地理解和应用这些重要的图论算法。
相关文章:

【数学建模】——前沿图与网络模型:新时代算法解析与应用
目录 1.图与网络的基本概念 1. 无向图和有向图 2. 简单图、完全图、赋权图 3. 顶点的度 4. 子图与图的连通性 2.图的矩阵表示 1. 关联矩阵 2. 邻接矩阵 3.最短路问题 1.Dijkstra 算法 2.Floyd 算法 4.最小生成树问题 1.Kruskal 算法 2.Prim 算法 5.着色问题 6.…...

视频分帧【截取图片】(YOLO目标检测【生成数据集】)
高效率制作数据集【按这个流程走,速度很顶】 本次制作,1059张图片【马路上流动车辆】 几乎就是全自动了,只要视频拍得好,YOLO辅助制作数据集就效率极高 视频中的图片抽取: 【由于视频内存过大,遇到报错执行…...

Redis7(二)Redis持久化双雄
持久化之RDB RDB的持久化方式是在指定时间间隔,执行数据集的时间点快照。也就是在指定的时间间隔将内存中的数据集快照写入磁盘,也就是Snapshot内存快照,它恢复时再将硬盘快照文件直接读回到内存里面。 RDB保存的是dump.rdb文件。 自动触发…...

发布支持TS的npm包
你现在有这么一个包,已经将他发布在npm上了,周下载量也还比较可观。美中不足的就是,这个包之前使用js写的,现在你想增加TS类型,提升用户使用体验,那么你现在可以做以下几个步骤 1.在你的包的根目录下创建一…...

计算机视觉9 全卷积网络
全卷积网络(Fully Convolutional Network,简称 FCN)在计算机视觉领域具有重要地位。 传统的卷积神经网络(CNN)在最后的输出层通常使用全连接层来进行分类任务。然而,全连接层会丢失空间信息,使得…...

02.C++入门基础(下)
1.函数重载 C支持在同一作用域中出现同名函数,但是要求这些同名函数的形参不同,可以是参数个数不同或者类型不同。这样C函数调用就表现出了多态行为,使用更灵活。C语言是不支持同一作用域中出现同名函数的。 1、参数类型不同 2、参数个数不同…...

【数据结构】探索排序的奥秘
若有不懂地方,可查阅我之前文章哦! 个人主页:小八哥向前冲~_csdn博客 所属专栏:数据结构_专栏 目录 排序的概念 几种排序方法介绍 冒泡排序 选择排序 插入排序 堆排序 向上调整建堆排序 向下调整建堆排序 希尔排序 快速…...

数据结构面试知识点总结3
#来自ウルトラマンティガ(迪迦) 1 线性表 最基本、最简单、最常用的一种数据结构。一个线性表是 n 个具有相同特性的数据元素的有限序列。 特征:数据元素之间是一对一的逻辑关系。 第一个数据元素没有前驱,称为头结点࿱…...
python-爬虫实例(5):将进酒,杯莫停!
目录 前言 将进酒,杯莫停! 一、浇给 二、前摇 1.导入selenium库 2.下载浏览器驱动 三、爬虫四步走 1.UA伪装 2.获取url 3.发送请求 4.获取响应数据进行解析并保存 总结 前言 博主身为一个农批,当然要尝试爬取王者荣耀的东西啦。 将进…...

AGI 之 【Hugging Face】 的【从零训练Transformer模型】之二 [ 从零训练一个模型 ] 的简单整理
AGI 之 【Hugging Face】 的【从零训练Transformer模型】之二 [ 从零训练一个模型 ] 的简单整理 目录 AGI 之 【Hugging Face】 的【从零训练Transformer模型】之二 [ 从零训练一个模型 ] 的简单整理 一、简单介绍 二、Transformer 1、模型架构 2、应用场景 3、Hugging …...

十大排序的稳定性和时间复杂度
十大排序算法的稳定性和时间复杂度是数据结构和算法中的重要内容。 以下是对这些算法的稳定性和时间复杂度的详细分析: 稳定性 稳定性指的是排序算法在排序过程中是否能够保持相等元素的原始相对顺序。根据这个定义,我们可以将排序算法分为稳定排序和…...
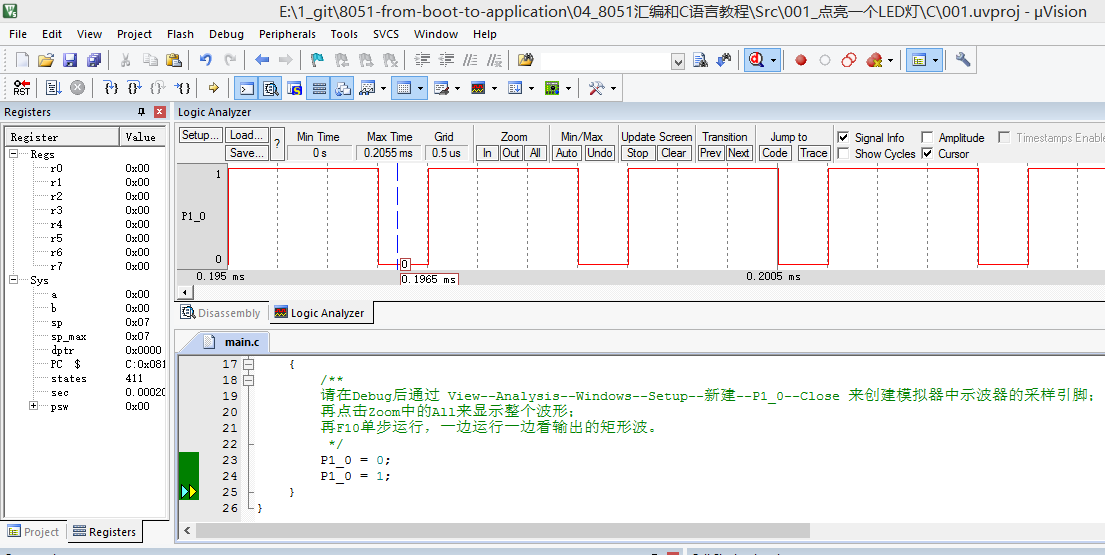
【系列教程之】1、点亮一个LED灯
1、点亮一个LED灯 作者将狼才鲸创建日期2024-07-23 CSDN教程目录地址:【目录】8051汇编与C语言系列教程本Gitee仓库原始地址:才鲸嵌入式/8051_c51_单片机从汇编到C_从Boot到应用实践教程 本源码包含C语言和汇编工程,能直接在电脑中通过Keil…...

搜维尔科技:Manus Metagloves使用精确的量子跟踪技术捕捉手部每一个细节动作
Manus Metagloves使用精确的量子跟踪技术捕捉手部每一个细节动作 搜维尔科技:Manus Metagloves使用精确的量子跟踪技术捕捉手部每一个细节动作...

机器学习 | 阿里云安全恶意程序检测
目录 一、数据探索1.1 数据说明1.2 训练集数据探索1.2.1 数据特征类型1.2.2 数据分布1.2.3 缺失值1.2.4 异常值1.2.5 标签分布探索 1.3 测试集探索1.3.1 数据信息1.3.2 缺失值1.3.3 数据分布1.3.4 异常值 1.4 数据集联合分析1.4.1 file_id 分析1.4.2 API 分析 二、特征工程与基…...

python打包exe文件-实现记录
1、使用pyinstaller库 安装库: pip install pyinstaller打包命令标注主入库程序: pyinstaller -F.\程序入口文件.py 出现了一个问题就是我在打包运行之后会出现有一些插件没有被打包。 解决问题: 通过添加--hidden-importcomtypes.strea…...

基本的DQL语句-单表查询
一、DQL语言 DQL(Data Query Language 数据查询语言)。用途是查询数据库数据,如SELECT语句。是SQL语句 中最核心、最重要的语句,也是使用频率最高的语句。其中,可以根据表的结构和关系分为单表查询和多 表联查。 注意:所有的查询…...

Vue3 对比 Vue2
相关信息简介2020年9月18日,Vue.js发布3.0版本,代号:One Piece(海贼王) 2 年多开发, 100位贡献者, 2600次提交, 600次 PR、30个RFC Vue3 支持 vue2 的大多数特性 可以更好的支持 Typescript,提供了完整的…...

2024中国大学生算法设计超级联赛(1)
🚀欢迎来到本文🚀 🍉个人简介:陈童学哦,彩笔ACMer一枚。 🏀所属专栏:杭电多校集训 本文用于记录回顾总结解题思路便于加深理解。 📢📢📢传送门 A - 循环位移解…...

offer题目51:数组中的逆序对
题目描述:在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数。例如,在数组{7,5,6,4}中,一共存在5个逆序对,分别是(7…...

45、PHP 实现滑动窗口的最大值
题目: PHP 实现滑动窗口的最大值 描述: 给定一个数组和滑动窗口的大小,找出所有滑动窗口里数值的最大值。 例如: 如果输入数组{2,3,4,2,6,2,5,1}及滑动窗口的大小3, 那么一共存在6个滑动窗口, 他们的最大值…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...
