P1113 杂务(拓扑排序 or 记忆回溯)
题目描述
John的农场在给奶牛挤奶前有很多杂务要完成,每一项杂务都需要一定的时间来完成它。比如:他们要将奶牛集合起来,将他们赶进牛棚,为奶牛清洗乳房以及一些其它工作。尽早将所有杂务完成是必要的,因为这样才有更多时间挤出更多的牛奶。当然,有些杂务必须在另一些杂务完成的情况下才能进行。比如:只有将奶牛赶进牛棚才能开始为它清洗乳房,还有在未给奶牛清洗乳房之前不能挤奶。我们把这些工作称为完成本项工作的准备工作。至少有一项杂务不要求有准备工作,这个可以最早着手完成的工作,标记为杂务1。John有需要完成的n个杂务的清单,并且这份清单是有一定顺序的,杂务k(k>1)的准备工作只可能在杂务1至k−1中。
写一个程序从1到n读入每个杂务的工作说明。计算出所有杂务都被完成的最短时间。当然互相没有关系的杂务可以同时工作,并且,你可以假定John的农场有足够多的工人来同时完成任意多项任务。
输入格式
第1行:一个整数n,必须完成的杂务的数目3≤n≤10,000);
第2至(n+1)行: 共有n行,每行有一些用1个空格隔开的整数,分别表示:
* 工作序号(1至n,在输入文件中是有序的);
* 完成工作所需要的时间(1≤len≤100);
* 一些必须完成的准备工作,总数不超过100个,由一个数字0结束。有些杂务没有需要准备的工作只描述一个单独的0,整个输入文件中不会出现多余的空格。
输出格式
一个整数,表示完成所有杂务所需的最短时间。
输入输出样例
输入 #1复制
7 1 5 0 2 2 1 0 3 3 2 0 4 6 1 0 5 1 2 4 0 6 8 2 4 0 7 4 3 5 6 0
输出 #1复制
23
题意:
需要先完成前面的任务才能进行下一步,任务间可以同时做。我们用贪心找在同时做的最大任务即可。
解析:
解法1:
用dfs记忆回溯算法,当到达最后一个点是一定是自己要的任务是时间要加进去的。
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
const int N = 10010;
int f[N];
int time1[N];
vector<int> a[N];
int dfs(int x) {if (f[x]) return f[x];//该节点已经遍历过了,减枝for (int i = 0; i < a[x].size(); i++) {f[x] = max(f[x], dfs(a[x][i])); //说有子集中最大的节点}f[x] += time1[x]; // 加上自己需要的时间return f[x];
}
int main() {int n;cin >> n;for (int i = 0; i < n; i++) {int x, y,z;cin >> x >> y >> z;time1[x] = y;while(z != 0){a[z].push_back(x);// 只有完成z 后才能完成 x 所以有z -> x的边scanf("%d", &z);}}int ans = 0;for (int i = 1; i <= n; i++) {ans = max(ans, dfs(i));}cout << ans<<endl;return 0;
}解法2:
用队列记录,拓扑排序,将入度为0的点push进队列中。
#include<iostream>
#include<vector>
#include<algorithm>
#include<queue>
using namespace std;
const int N = 10010;
int f[N];
int time1[N];
vector<int> a[N];
int in[N];
int main() {queue<int> q;int n;cin >> n;for (int i = 0; i < n; i++) {int x, y,z;cin >> x >> y >> z;time1[x] = y;while(z != 0){a[z].push_back(x);// 只有完成z 后才能完成 x 所以有z -> x的边scanf("%d", &z);in[x]++;}}int ans = 0;for (int i = 1; i <= n; i++) {if (in[i] == 0) {q.push(i);f[i] = time1[i];//记录需要的时间}}while (!q.empty()) {int pro = q.front();q.pop();for (int i = 0; i < a[pro].size(); i++) {int u = a[pro][i];in[u]--;if (in[u] == 0) q.push(u); //入度为0f[u] = max(f[u], f[pro]+time1[u]);//到达这个点中最大的时间}}for (int i = 1; i<= n; i++) {ans = max(ans, f[i]);}cout << ans<<endl;return 0;
}相关文章:
)
P1113 杂务(拓扑排序 or 记忆回溯)
题目描述 John的农场在给奶牛挤奶前有很多杂务要完成,每一项杂务都需要一定的时间来完成它。比如:他们要将奶牛集合起来,将他们赶进牛棚,为奶牛清洗乳房以及一些其它工作。尽早将所有杂务完成是必要的,因为这样才有更…...

Web3中文|政策影响下的新加坡Web3步伐喜忧参半
如果说“亚洲四小龙”是新加坡曾经的荣耀,那么当时代进入21世纪的第二个十年,用新加坡经济协会(SEE)副主席、新加坡新跃社科大学教授李国权的话来说,新加坡现在的“荣耀”是全球金融的主要“节点”或区块链行业发展的关…...

Java数据库高阶面试题,好程序员学员分享百度Java面试流程
小源下面分享一位好程序员的学员去百度Java面试流程!百度技术一面(20分钟)1、自我介绍很流畅捡重点介绍2、数据结构算法好不好挺好的(其实心还是有点虚,不过最近刷了很多好程序员出的题感觉没问题!)3、找到单链表的三等分点,如果单…...
)
栈和队列习题精选(持续更新中)
第一题(括号匹配)给定一个只包括 (,),{,},[,] 的字符串 s ,判断字符串是否有效。有效字符串需满足:1.左括号必须用相同类型的右括号闭合。2.左括号必须以正确的顺序闭合。…...
大数据开发 - Java入门6
目录标题do-while循环练习1:从键盘输入单词,讲输入的单词输出到控制台,输入是exit时退出循环练习2:键盘输入密码和确认密码,两次密码一致就退出循环打印注册成功,两次密码不一致就循环输入两次密码死循环fo…...
开源超级终端工具——WindTerm
1、下载和安装(我的是win10,其他版本各位自选) Releases kingToolbox/WindTerm GitHub 安装的话,相信大家不用我赘述了。 初始界面是这样的: 2、WindTerm使用 2.1 本地会话(最下面那个框,发…...

【Linux】信号常见概念
文章目录信号入门生活中的信号技术应用角度的信号signal函数注意事项信号的概念信号的产生信号的记录(保存)信号处理常见方式概述信号入门 生活中的信号 你在网上买了很多件商品,在等待不同商品快递的到来 但即便快递还没有到来,你也知道快递到了的时候应该怎么处理快递,也就…...

15000 字的 SQL 语句大全 第一部分
一、基础 1、说明:创建数据库CREATE DATABASE database-name 2、说明:删除数据库drop database dbname 3、说明:备份sql server--- 创建 备份数据的 device USE master EXEC sp_addumpdevice disk, testBack, c:\mssql7backup\MyNwind_1.dat …...

突发——字节跳动被要求出售 TikTok 股票,否则禁令,低代码也曾被打压
一、欲加之罪,何患无辞! 正值人们对TikTok和其它社交媒体平台对年轻用户的影响进行更广泛、持续的反思之际,美政客们以数据安全为由要求TikTok出售股票,已然不顾文明国家的体面。 在美国,TikTok拥有1.4亿用户&#x…...

2023年网络安全趋势
数据安全越来越重要。 我国《数据安全法》提出“建立健全数据安全治理体系”,各地区部门均在探索和简历数据分类分级、重要数据识别与重点保护制度。 数据安全治理不仅是一系列技术应用或产品,更是包括组织构建、规范制定、技术支撑等要素共同完成数据…...
html练习
1.用户注册界面 代码: <!DOCTYPE html> <html><head><meta charset"utf-8"><title></title></head><body><form action"#" method"get"><table border"1" widt…...

【Redis】Redis 是如何保证高可用的?(背诵版)
Redis 是如何保证高可用的?1. 说一下 Redis 是如何保证高可用的?2. 了解过主从复制么?2.1 Redis 主从复制主要的作用是什么?2.2 Redis 主从模式的拓扑结构?(1)一主一从结构(2)一主多…...

Qt---去掉标题栏后,最大化应用程序窗口时,窗口遮住了任务栏
// showMaximized(); // Qt最大化显示函数 任务栏都会覆盖static bool max false;static QRect location this->geometry();if (max) {this->setGeometry(location);//回复窗口原大小和位置// ui->maxBtn->setIcon(QIcon(":/MAX_.png"));}else {// ui-…...
报告详解)
Cadence Allegro 导出Netin(non-back)报告详解
⏪《上一篇》 🏡《上级目录》 ⏩《下一篇》 目录 1,概述2,Netin(non-back)作用3,Netin(non-back)示例4,Netin(non-back)导出方法4.1,方法1:4.2,方法2:B站关注“硬小二”浏览更多演示视频...
HTML语言
1.什么是HTML? 1、HTML是超文本标记语言(Hyper Text Markup Language) 2、HTML由各种各样的标签(tag)组成,如、 3、HTML文档 网页 (1)一种纯文本文件,扩展名为.html或.html; (2)最终显示结果取决…...

线性代数之行列式
一、思维导图二、二阶、三阶行列式的定义1、二阶行列式2、三阶行列式沙路法展开3、解方程3.1解二元一次方程组观察上面两个未知量的值不难发现,它 们的分母均是上述方程组未知量的系数形成的二阶行列式,𝑥1的分子是将系数行列 式的第一列换成…...

【FPGA-Spirit_V2】小精灵V2开发板初使用
🎉欢迎来到FPGA专栏~小精灵V2开发板初使用 ☆* o(≧▽≦)o *☆嗨~我是小夏与酒🍹 ✨博客主页:小夏与酒的博客 🎈该系列文章专栏:FPGA学习之旅 文章作者技术和水平有限,如果文中出现错误,希望大家…...
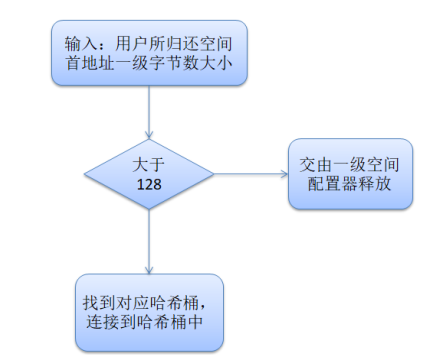
STL与其空间配置器
目录什么是STLSTL的六大组件STL的缺陷什么是空间配置器为什么需要空间配置器GI-STL空间配置器实现原理一级空间配置器二级空间配置器内存池SGI-STL中二级空间配置器设计SGI-STL二级空间配置器之空间申请前期的准备申请空间填充内存块向内存池中索要空间SGI-STL二级空间配置器之…...
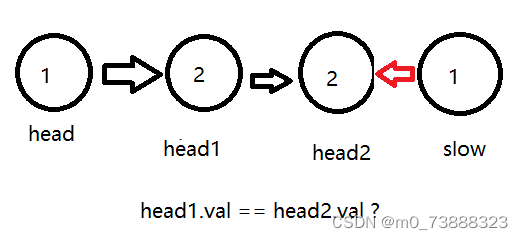
leetcode刷题之回文链表
目录 做题思路 代码实现 1.找到链表的中间节点 2.反转中间节点之后的链表 3.判断倒置的后半部分的链表是否等于前半部分的链表 整体代码展示 总结: 这里是题目链接。 这道题目的意思是:判断该链表中后半部分倒置是否跟前半部分相同,如…...

复制带随机指针的链表最长连续递增序列数组的度写字符串需要的行数最短补全词
复制带随机指针的链表来源:杭哥138. 复制带随机指针的链表 - 力扣(LeetCode)typedef struct Node Node; Node* BuyNode(int x) {Node* newnode (Node*)malloc(sizeof(Node));newnode->valx;newnode->nextNULL;newnode->randomNULL;…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...
