01背包问题c++
问题
问题介绍
有 N 种物品和一个容量是 V 的背包,每种物品都有无限件可用。
第 i 种物品的体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品种数和背包容积。
接下来有 N 行,每行两个整数 vi,wi,用空格隔开,分别表示第 i 种物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
讲解
首先要说明的就是,本教程只讲解一般的写法,不讲解优化方法(滚动数组降维),先把基本的思想学会了,然后再去学优化方法的。
相信大多数人刚开始学dp问题的时候碰到的就是01背包问题,dp问题首先就是先定义dp数组所代表的意义(比如说这道题,dp[i][j]所代表的就是选取前i个物品体积不会超过j的最大价值),然后就是判断每一步的状态(比如说这一题就是每一步都要判断是否选择这个物品),然后就是状态转移方程了。
回归本题目,本题的思想就是装前i个物品,然后体积一直增大,每次就是判断选不选这个物品,
- 如果选这个物品的价值就是
dp[i - 1][j - v[i]] + w[i]
解析:选这一个那么肯定要加上这一个的价值w[i]这里应该没有问题了吧,那为什么前面是dp[i - 1][j - v[i]]呢?因为就是选了这一个物品了,这一个物品占据了v[i]的体积,那么只要找到子问题选i-1个物品,然后体积不大于j-v[i]的最优解就可以了。 - 如果不选这个物品,就直接从前i-1个物品选体积不大于j的最优解了。
- 每次判断一下,就是如果这个物品的体积大于现在所能装的最大的体积,那么肯定就是直接不能选择这个物品了。
图解
- 图片中在中间价值数据中被标黄的数据就是当前物品的体积大于背包当前所能装的最大体积,所以直接就不用选这个物品,直接将上一层的数据拉下来就行了。
- 图片可能会不好看哈,等我优化。

基础源码
#include <bits/stdc++.h>using namespace std;const int N = 1010;int n, k;
int v[N], m[N];
int dp[N][N];int main()
{cin >> n >> k;for (int i = 1; i <= n; i ++ ) cin >> v[i] >>m[i];for (int i = 1; i <= n; i ++ ){for (int j = 1; j <= k; j ++ ){if (v[i] > j){dp[i][j] = dp[i - 1][j];}else{dp[i][j] = max(dp[i - 1][j - v[i]] + m[i], dp[i - 1][j]);}}}cout << dp[n][k] << endl;}
一维数组优化
- 来自几个小时后的我:看了一下y总的视频,突然就会了一维数组的优化方法是怎么写的了。
- 其实如果上面那个图你从头推了一遍,你就会发现我们更新每一层的数据的时候,其实只用到了上一层的数据而且还是用到上一层数据的范围为–>从上一层起点开始到本层数据正上方的数据。比如说我们要更新第三层第4列的数据,那么其实我们用到的数据范围为,第3-1层第一列到第3-1层第4列。
- 我们遍历j的时候要从后(最大的体积)向前遍历到
v[i]。- 为什么要从后开始遍历呢?
因为我们每次更新要用到前面的数据,如果我们从前向后更新,当我们遍历到后边的时候要用到前面的数据但是前面的数据已经更改了,不是第i-1层的数据了,所以我们要从后向前遍历,这样就不会影响到前面的数据。 - 为什么遍历到v[i]就可以了呢?
因为就是j<v[i]的时候肯定是不能选这个物品的,直接就是拉取正上方的数据就行,也就相当于不用更改数据。
- 为什么要从后开始遍历呢?
一维数组优化后源码
#include <iostream>using namespace std;const int N = 1010;int dp[N];
int v[N], w[N];int main()
{int n, m;cin >> n >> m;for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];for (int i = 1; i <= n; i ++ ){for (int j = m; j >= v[i]; j -- ){dp[j] = max(dp[j], dp[j - v[i]] + w[i]);}}cout << dp[m] << '\n';return 0;}
相关文章:

01背包问题c++
问题 问题介绍 有 N 种物品和一个容量是 V 的背包,每种物品都有无限件可用。 第 i 种物品的体积是 vi,价值是 wi。 求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。 输出最大价值。 输入格式 第…...
ZYNQ硬件调试-------day2
ZYNQ硬件调试-------day2 1.ILA(Integrated Logic Analyzer ) 监控逻辑内部信号和端口信号;可以理解为输出。可单独使用 2.VIO(Virtual Input/Output ) 实时监控和驱动逻辑内部信号和端口信号,可以理解为触发输入。不可…...

JavaScript中Promise的简单使用及其原理
Promise是ES6最重要的特性之一,今天来系统且细致的研究一下Promise的用法以及原理。 按照我往常的理解,Promise是一个构造函数,有all、resolve、reject、then、catch等几个方法,一般情况下,在涉及到异步操作时才会用到…...
SpringBoot RabbitMQ 延时队列取消订单【SpringBoot系列14】
SpringCloud 大型系列课程正在制作中,欢迎大家关注与提意见。 程序员每天的CV 与 板砖,也要知其所以然,本系列课程可以帮助初学者学习 SpringBooot 项目开发 与 SpringCloud 微服务系列项目开发 1 项目准备 SpringBoot 雪花算法生成商品订单…...

【论文阅读 WWW‘23】Zero-shot Clarifying Question Generation for Conversational Search
文章目录前言MotivationContributionsMethodFacet-constrained Question GenerationMultiform Question Prompting and RankingExperimentsDatasetResultAuto-metric evaluationHuman evaluationKnowledge前言 最近对一些之前的文章进行了重读,因此整理了之前的笔记…...
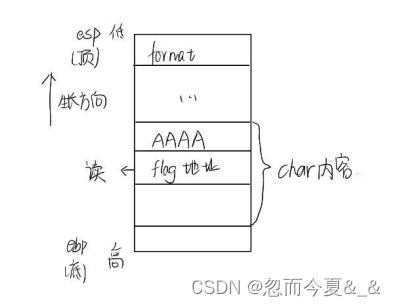
ouc 网络安全实验 格式化字符串漏洞
文章目录要求lab1lab2lab3lab4结语因为当时自己做实验的时候出现了很多疑问不会解决,在网上看到了一位大佬 王森ouc 的专栏文章解决了很多问题,也学到了很多知识和解决问题的方法,现在把我的实验解决方法也发上来,希望有不会的同…...
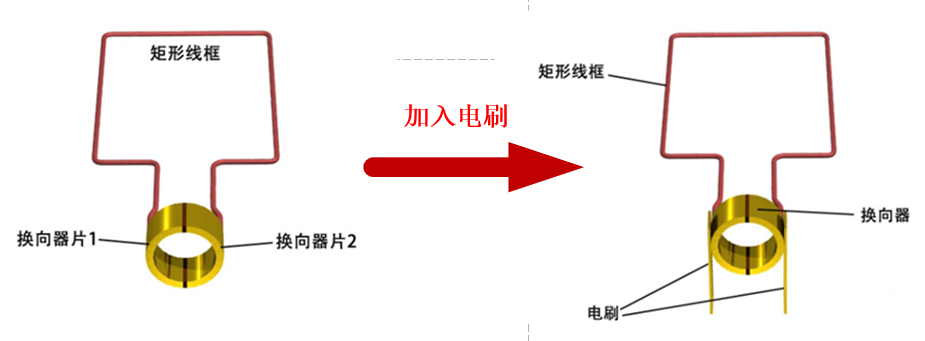
PMSM矢量控制笔记(1.1)——电机的机械结构与运行原理
前言:重新整理以前的知识和文章发现,仍然有许多地方没有学得明白,懵懵懂懂含含糊糊的地方多如牛毛,尤其是到了真正实际写东西或者做项目时,如果不是系统的学习了知识,很容易遇到问题就卡壳,也想…...
网络安全竞赛试题——中间人攻击渗透测试解析(详细))
2022年全国职业院校技能大赛(中职组)网络安全竞赛试题——中间人攻击渗透测试解析(详细)
B-4任务四:中间人攻击渗透测试 *任务说明:仅能获取Server4的IP地址 *任务说明:仅能获取Server11的IP地址 1.通过上题渗透后得到控制权限的服务器场景Server4进行查看本地的arp缓存表的操作,并将该操作所使用的命令作为Flag值提交; 2.通过上题渗透后得到控制权限的服务…...

MySQL必知必会 | 安全、维护、性能
全球化和本地化 关于MySQL处理不同字符集和语言 字符集和校对顺序 数据库被用来存储和检索数据,不同的语言和字符集需要以不同的方式存储和检索,因此,MySQL需要适应不同的字符集,适应不同的排序方式 一些术语: 字符…...

MaaS Model as a Service 模型即服务
大模型是人工智能的发展趋势和未来。大模型是“大算力强算法” 结合的产物。目前,大模型生态已初具规模。大模型能够实现 AI 从“手工作坊”到“工厂模式”的转变,大模型通常是在大规模无标注 数据上进行训练,学习出一种特征和规则…...
)
【编程基础】027.C语言中函数在解题中的应用(三)
文章目录C语言中函数的应用1、自定义函数实现二维数组的转置2、自定义函数之整数处理3、自定义函数之数字后移4、自定义函数之字符串拷贝C语言中函数的应用 1、自定义函数实现二维数组的转置 题目描述 写一个函数,使给定的一个二维数组(3&a…...
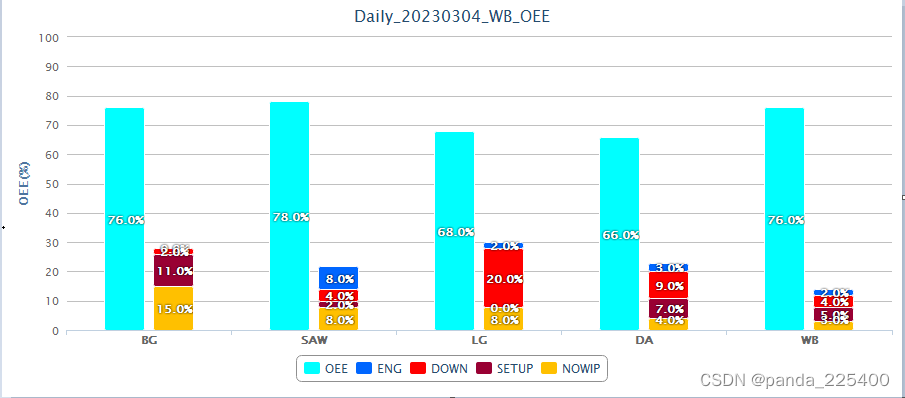
echart图表之highcharts
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录前言一、HighCharts是什么?二、使用步骤1.引入库2.前端代码3.展现结果4.后台自动截图总结前言 提示:这里可以添加本文要记录的大概内容&…...

关于.Net和Java的看法——我见过最牛的一个小实习生经历
1、背景 笔者(小方同学在学习)是一个专科院校的一名普通学生,目前就职于某三线城市的WEB方面.Net开发实习生,在找实习期间和就业期间的一些看法,发表此文,纯个人想法,欢迎讨论,指正…...
基于springboot+vue的“智慧食堂”程序设计实现【毕业论文,源码】
系统登录界面系统架构开发语言:Java框架:springbootJDK版本:JDK1.8服务器:tomcat7数据库:mysql 5.7数据库工具:Navicat开发软件:eclipse/myeclipse/ideaMaven包:Maven浏览器…...

学计算机选择什么编程语言好一些?
工资水平的话,目前人工智能、大数据和云计算等领域的工资相对较高,但是要求也高,学历,学习能力什么的。然后是后端开发,Python、Java、C等编程语言的工资普遍较高。 不用开发语言的优势 Java:Java是一种…...

持续集成 在 Linux 上搭建 Jenkins,自动构建接口测试
本篇把从 0 开始搭建 Jenkins 的过程分享给大家,希望对小伙伴们有所帮助。 文章目录 在 Linux 上安装 Jenkins在 Linux 上安装 Git在 Linux 上安装 Python在 Linux 上安装 Allure配置 Jenkinsjenkins 赋能 - 使用邮箱发送测试报告jenkins 赋能 - 优化测试报告内容…...
)
MySQL学习笔记(总结)
1. 数据库服务器操作命令 启动数据库:net start mysql80 (注释:windows命令) 停止数据库:net stop mysql80 (注释:windows命令) 重启数据库:systemctl restart mysql;…...
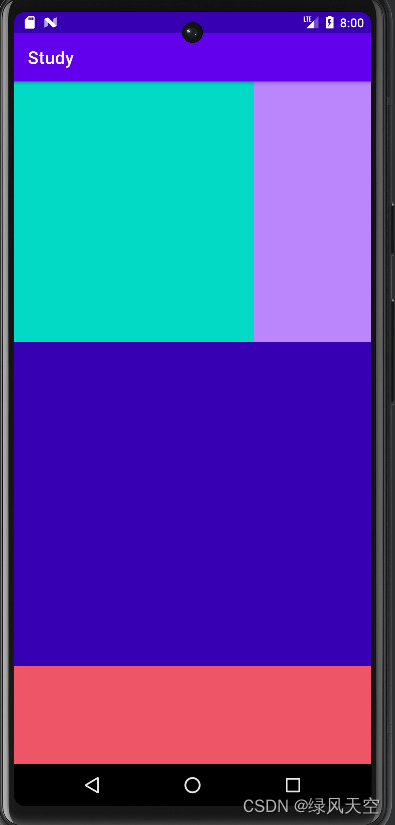
Android开发 Layout布局 ScrollView
1.LinearLayout 属性 orientation:内部组件排列方式,可选vertical、horizontal,默认horizontal layout_weight: 与平级组件长宽比例,需要将layout_width、layout_height其中一个设置为0dp,表明长或宽与平级组件的长…...
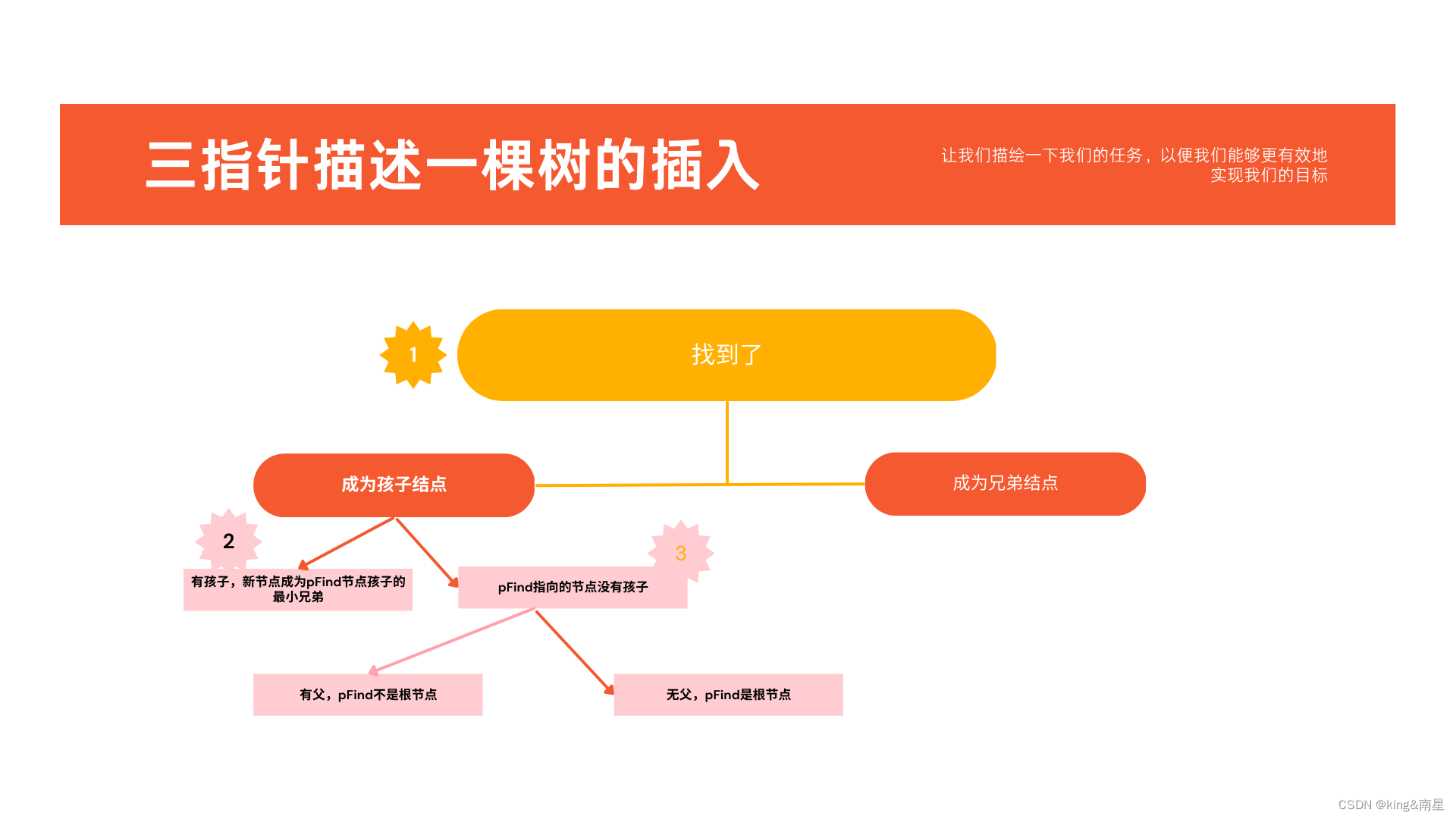
手撕数据结构与算法——树(三指针描述一棵树)
🏆作者主页:king&南星 🎄专栏链接:数据结构 🏅文章目录🌱树一、🌲概念与定义二、🌳定义与预备三、🌴创建结点函数四、🍀查找五、🍁插入六、&a…...

字节跳动Java后端开发实习面经
最近在和同学一起找实习,投了b站、字节和miHoYo的后端开发。b站二月底就投了,但现在也还没回复;miHoYo也还没回复,估计是只面向24届了;感谢字节,给了我面试的机会。字节真的处理好快,不到一周官…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...
