数据结构·AVL树
1. AVL树的概念
二叉搜索树虽可以缩短查找的效率,但如果存数据时接近有序,二叉搜索将退化为单支树,此时查找元素效率相当于在顺序表中查找,效率低下。因此两位俄罗斯数学家 G.M.Adelson-Velskii 和E.M.Landis 在1962年发明了一种解决上述问题的方法:当二叉搜索树中插入新节点后,如果能保证每个节点的左右子树高度差不大于 1 的绝对值,即可降低树的高度,从而减少平均搜索长度。
一个标准的AVL树任意节点的左右子树高度差的绝对值不大于1,我们将记录高度差的数据称为平衡因子。
平衡因子 = 右子树高度 - 左子树高度

2. AVL树节点的定义

我们根STL库保持一致,将key和value合并定义成pair类型,再在节点中添加一个平衡因子。
3. AVL树的插入
关于平衡因子,我们可以通过其定义得知这样两条条性质:
1. 插入节点时只会影响到祖先的平衡因子,而不会影响到其他节点的平衡因子。
2. 父节点右侧插入节点其平衡因子 +1,左侧插入节点其平衡因子 -1
对于插入节点的父节点来说,插入后父节点的平衡因子只会出现3种情况:第一种情况是平衡因子为0 、第二种情况是平衡因子为1 或 -1 、第三种情况是有祖先平衡因子出现 2 或 -2
插入后父节点平衡因子为0时
说明在左侧或右侧插入一个节点后,父节点平衡了,但此时并不会影响除父节点外的所有祖先的平衡因子,因此平衡因子不需要再向上更新了。

插入后父节点平衡因子为 1 或 -1 时
说明父节点之前的平衡因子一定为0,左侧插入能使父节点变-1,右侧插入能使父节点变1。为什么父节点平衡因子之前一定为0?因为AVL树的平衡因子只可能出现-1、0、1三种情况。
此时平衡因子需要向上更新

插入后有祖先平衡因子出现 2 或 -2
说明这个祖先更新前是1或-1,新节点插入在高的那棵树上,进一步加剧了高差,此时已经违反高差不大于1的规则了,此时需要旋转处理

平衡因子调整的逻辑就是这样添加到insert函数中的,我会把完整的代码贴到最后的

4. AVL树的旋转
4.1 左单旋
插入节点在较高右子树的右侧时就要进行左单旋。

我这个图中的长方形就代表一颗子树。下面外我们基于这个旋转逻辑编写代码
经过我们前面更新平衡因子之后找到不符合规则的父节点30,我们进行旋转代码编写的时候不仅仅要弄节点向下的链接内容,还要记得修改节点的parent指针,也就是向上链接的内容。
我们要更改的主要就是 30(parent节点) 60(subR节点) tree_b(subRL)

但是我们把代码写成这个还是不对的,因为parent的parent没有向下链接。在它向下链接的过程中还有两种情况:就是parent本身就是整颗树的根节点,旋转后subR成为整棵树的根节点;或parent只是树中的一个普通节点,那就要考虑parent的parent向下链接的时候链接左子树还是右子树了。

4.2 右单旋
当要在较高左子树的左侧插入新节点就要进行右单旋

右单旋的思路和代码和左单旋是一样的,反过来而已,先向下更新链接内容,再向上更新链接内容,然后更新parentParent的向下链接,最后调整平衡因子

4.3 右左双旋
当新节点插入在较高右子树的左侧时就要进行右左双旋。

如果我们单纯以30为parent或者说旋转基点进行单左旋,结果就是60这棵子树变成30的右子树,但是这棵树还是不平衡的,c比d高出了2,此时再以90为基点右旋结果就是又回去了。
当较高的树在最两侧的时候我们进行单左旋或单右旋是可以让树平衡的,但是如果较高的树在中间的时候我们进行单左右旋就会让这个较高树一直在中间来回变动,而树一直不会平衡。
所以AVL就用我图中的方案解决了这一问题。

但是如果我们直接把代码写成这样肯定是不行的,因为平衡因子的问题还没有得到更新。
如果是我图中画的情况也就是说插入在c树中最后的平衡因子就是 -1、0、0
如果新节点插入在b树中,最后平衡因子就应该是 0、0、1
如果 h=0,也就是说60是新插入的节点,最后的平衡因子就应该是 0、0、0
那具体是这三种情况中的哪种,我们可以通过观察插入后60节点的平衡因子来判断

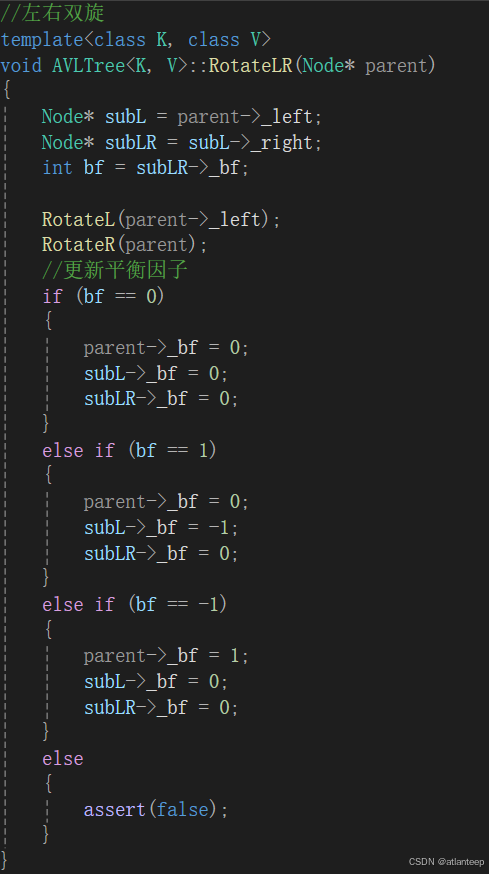
4.4 左右双旋
当在较高左子树右侧插入新节点时要进行左右双旋

代码与右左双旋一个思路,注意最后要调整平衡因子。
5. AVL树代码
删除的思路和插入是一致的,但是删除的更新平衡因子会比较复杂,因为删除在旋转了之后平衡因子可能还要继续向上更新。今天先不写删除了,如果之后有精力我会把删除更新上的。
#include<assert.h>
#include<iostream>
using namespace std;template<class K, class V>
struct AVLTNode
{AVLTNode(const pair<K, V>& kv): _kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr), _bf(0){}pair<K, V> _kv;AVLTNode<K, V>* _left;AVLTNode<K, V>* _right;AVLTNode<K, V>* _parent;int _bf; //balance factor 平衡因子
};template<class K, class V>
class AVLTree
{typedef AVLTNode<K, V> Node;public://构造AVLTree() = default;//拷贝构造AVLTree(const AVLTree<K, V>& t){_root = Copy(t._root);}//赋值运算符重载void operator=(const AVLTree<K, V>& t){AVLTree<K, V> new_t(t);std::swap(new_t._root, _root);}//析构~AVLTree(){Destroy(_root);_root = nullptr;}void Destroy(Node* root){if (root == nullptr)return;Destroy(root->_left);Destroy(root->_right);delete root;}Node* Copy(const Node* root){if (root == nullptr)return nullptr;Node* newnode = new Node(root->kv);newnode->_left = Copy(root->_left);newnode->_right = Copy(root->_right);return newnode;}//插入bool Insert(const pair<K, V>& kv);//搜索Node* Find(const K& x);//中序遍历void InOrder(){_InOrder(_root);cout << endl;}//树的高度int Height(){return _Height(_root);}//统计节点总个数(插入时可能会有重复数据)int Size(){return _Size(_root);}private://左单旋void RotateL(Node* parent);//右单旋void RotateR(Node* parent);//右左双旋void RotateRL(Node* parent);//左右双旋void RotateLR(Node* parent);//中序遍历(子函数)void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << endl;_InOrder(root->_right);}//树的高度int _Height(Node* root){if (root == nullptr)return 0;int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;}//统计节点总个数(插入时可能会有重复数据)int _Size(Node* root){return root == nullptr ? 0 : _Size(root->_left) + _Size(root->_right) + 1;}private:Node* _root = nullptr;
};//插入
template<class K, class V>
bool AVLTree<K, V>::Insert(const pair<K, V>& kv)
{//链表为空特殊处理if (_root == nullptr){_root = new Node(kv);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}elsereturn false;}cur = new Node(kv);if (cur->_kv.first < parent->_kv.first){parent->_left = cur;cur->_parent = parent;}else{parent->_right = cur;cur->_parent = parent;}//更新平衡因子while (parent){if (cur == parent->_left)parent->_bf--;elseparent->_bf++;if (parent->_bf == 0)break;else if (parent->_bf == -1 || parent->_bf == 1){//继续向上更新cur = parent;parent = parent->_parent;}else if (parent->_bf == -2 || parent->_bf == 2){//不平衡了,旋转处理if (parent->_bf == 2 && cur->_bf == 1)//左旋情况{RotateL(parent);}else if (parent->_bf == -2 && cur->_bf == -1)//右旋情况{RotateR(parent);}else if (parent->_bf == 2 && cur->_bf == -1)//右左双旋{RotateRL(parent);}else if (parent->_bf == -2 && cur->_bf == 1)//左右双旋{RotateLR(parent);}break;//旋完就退出更新}else{//出现其他奇奇怪怪的情况直接报错assert(false);}}return true;
} //搜索
template<class K, class V>
AVLTNode<K, V>* AVLTree<K, V>::Find(const K& x)
{Node* cur = _root;while (cur){if (cur->_kv.first < x){cur = cur->_right;}else if (cur->_kv.first > x){cur = cur->_left;}else{return cur;}}return nullptr;
}//左单旋
template<class K, class V>
void AVLTree<K, V>::RotateL(Node* parent)
{Node* subR = parent->_right;Node* subRL = parent->_right->_left;//修改向下链接内容parent->_right = subRL;subR->_left = parent;//修改向上链接内容subR->_parent = parent->_parent;parent->_parent = subR;if (subRL)//防止该树点为空{subRL->_parent = parent;}//parent的parent向下链接Node* parentParent = subR->_parent;if (parentParent == nullptr)//整棵树的根{_root = subR;}else{if (parent == parentParent->_right){parentParent->_right = subR;}else{parentParent->_left = subR;}}//调整平衡因子parent->_bf = 0;subR->_bf = 0;
}//右单旋
template<class K, class V>
void AVLTree<K, V>::RotateR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;//修改向下链接内容parent->_left = subLR;subL->_right = parent;//修改向上链接属性subL->_parent = parent->_parent;parent->_parent = subL;if (subLR){subLR->_parent = parent;}//修改parentParentNode* parentParent = subL->_parent;if (parentParent == nullptr){_root = subL;}else{if (parent == parentParent->_right){parentParent->_right = subL;}else{parentParent->_left = subL;}}//更新平衡因子subL->_bf = 0;parent->_bf = 0;
}//右左双旋
template<class K, class V>
void AVLTree<K, V>::RotateRL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(parent->_right);RotateL(parent);//更新平衡因子if (bf == 0){parent->_bf = 0;subR->_bf = 0;subRL->_bf = 0;}else if (bf == 1){parent->_bf = -1;subR->_bf = 0;subRL->_bf = 0;}else if (bf == -1){parent->_bf = 0;subR->_bf = 1;subRL->_bf = 0;}else{assert(false);}
}//左右双旋
template<class K, class V>
void AVLTree<K, V>::RotateLR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotateL(parent->_left);RotateR(parent);//更新平衡因子if (bf == 0){parent->_bf = 0;subL->_bf = 0;subLR->_bf = 0;}else if (bf == 1){parent->_bf = 0;subL->_bf = -1;subLR->_bf = 0;}else if (bf == -1){parent->_bf = 1;subL->_bf = 0;subLR->_bf = 0;}else{assert(false);}
}
相关文章:

数据结构·AVL树
1. AVL树的概念 二叉搜索树虽可以缩短查找的效率,但如果存数据时接近有序,二叉搜索将退化为单支树,此时查找元素效率相当于在顺序表中查找,效率低下。因此两位俄罗斯数学家 G.M.Adelson-Velskii 和E.M.Landis 在1962年发明了一种解…...
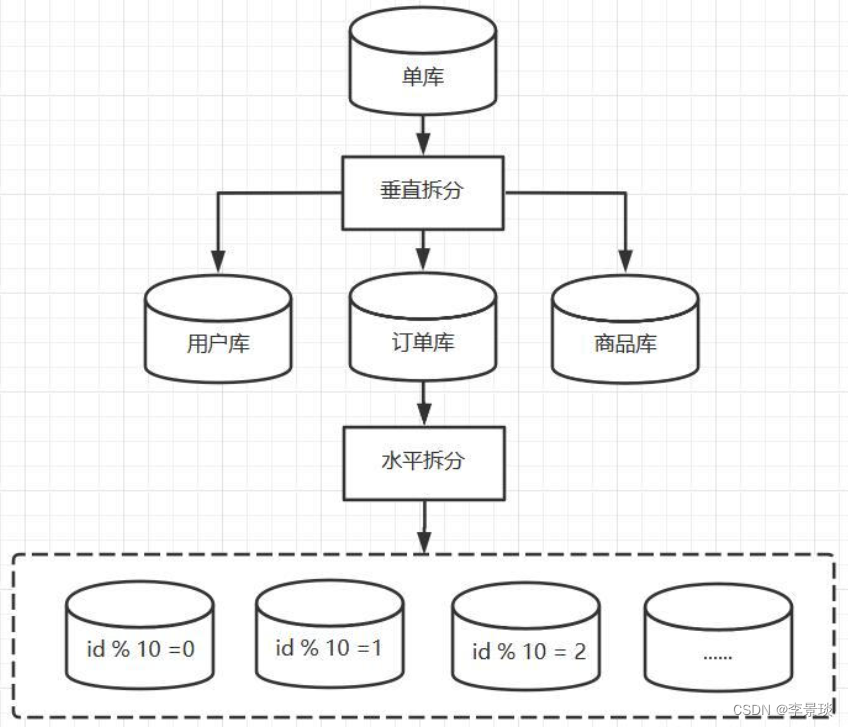
记一次Mycat分库分表实践
接了个活,又搞分库分表。 一、分库分表 在系统的研发过程中,随着数据量的不断增长,单库单表已无法满足数据的存储需求,此时就需要对数据库进行分库分表操作。 分库分表是随着业务的不断发展,单库单表无法承载整体的数据存储时,采取的一种将整体数据分散存储到不同服务…...
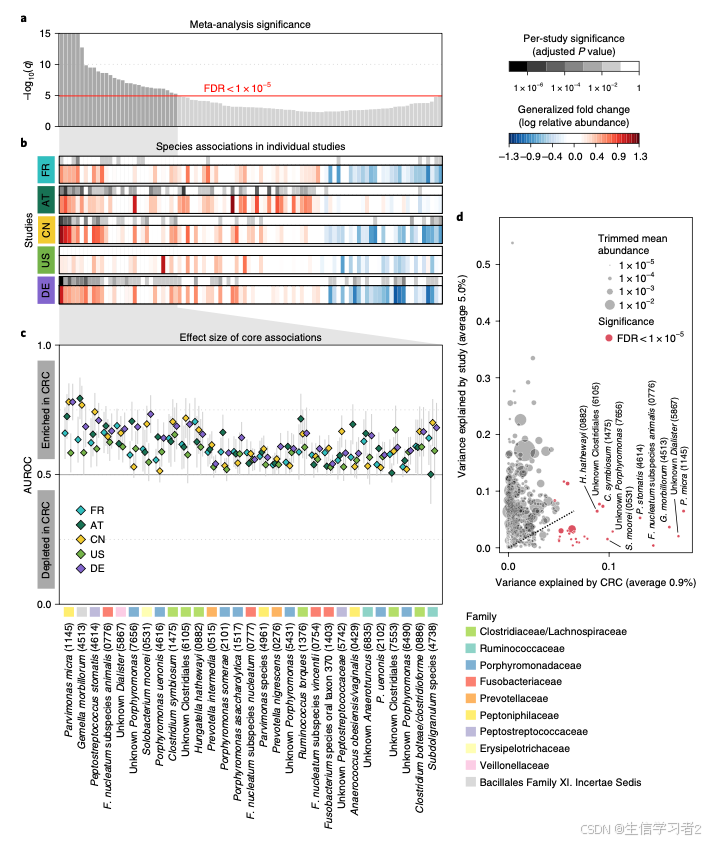
数据分析:微生物数据的荟萃分析框架
介绍 Meta-analysis of fecal metagenomes reveals global microbial signatures that are specific for colorectal cancer提供了一种荟萃分析的框架,它主要基于常用的Wilcoxon rank-sum test和Blocked Wilcoxon rank-sum test 方法计算显著性,再使用分…...
Django—admin后台管理
Django官网 https://www.djangoproject.com/ 如果已经有了Django跳过这步 安装Django: 如果你还没有安装Django,可以通过Python的包管理器pip来安装: pip install django 创建项目: 使用Django创建一个新的项目: …...
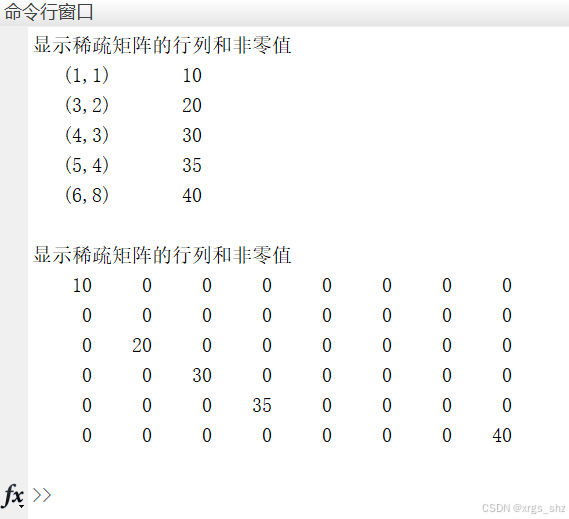
数字图像处理中的常用特殊矩阵及MATLAB应用
一、前言 Matlab的名称来源于“矩阵实验室(Matrix Laboratory)”,其对矩阵的操作具有先天性的优势(特别是相对于C语言的数组来说)。在数字图像处理中,为了提高编程效率,我们可以使用多种方式来创…...
精彩案例剖析一)
vue侦听器(Watch)精彩案例剖析一
目录 watch介绍 监视普通数据类型 监视对象类型 watch介绍 在 Vue 中,watch主要用于监视数据的变化,并执行相应操作。一旦被监视的属性发生变化,回调函数将自动被触发。当在 Vue 中使用watch来响应数据变化时,首先要清楚,watch本质上是一个对象,且必须以对象的…...

HTTP 协议浅析
HTTP(HyperText Transfer Protocol,超文本传输协议)是应用层最重要的协议之一。它定义了客户端和服务器之间的数据传输方式,并成为万维网(World Wide Web)的基石。本文将深入解析 HTTP 协议的基础知识、工作…...
VsCode | 让空文件夹始终展开不折叠
文章目录 1 问题引入2 解决办法3 效果展示 1 问题引入 可能很多小伙伴更新VsCode或者下载新版本时候 ,创建的文件 会出现xxx文件夹/xxx文件夹,看着很不舒服,所以该如何展开所有空文件夹呢? 2 解决办法 找到VsCode的设置 &…...

Centos7_Minimal安装Cannot find a valid baseurl for repo: base/7/x86_6
问题 运行yum报此问题 就是没网 解决方法 修改网络信息配置文件,打开配置文件,输入命令: vi /etc/sysconfig/network-scripts/ifcfg-网卡名字把ONBOOTno,改为ONBOOTyes 重启网卡 /etc/init.d/network restart 网路通了...
Spark_Oracle_II_Spark高效处理Oracle时间数据:通过JDBC桥接大数据与数据库的分析之旅
接前文背景, 当需要从关系型数据库(如Oracle)中读取数据时,Spark提供了JDBC连接功能,允许我们轻松地将数据从Oracle等数据库导入到Spark DataFrame中。然而,在处理时间字段时,可能会遇到一些挑战…...
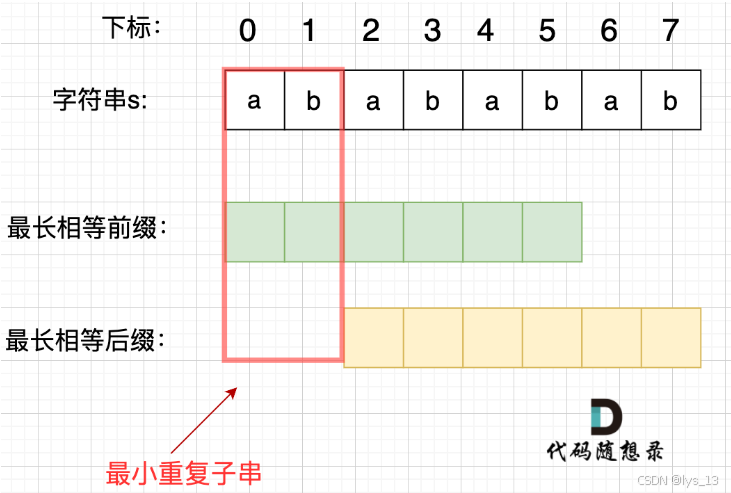
力扣 459重复的子字符串
思路: KMP算法的核心是求next数组 next数组代表的是当前字符串最大前后缀的长度 而求重复的子字符串就是求字符串的最大前缀与最大后缀之间的子字符串 如果这个子字符串是字符串长度的约数,则true /** lc appleetcode.cn id459 langcpp** [459] 重复…...

MyBatis XML配置文件
目录 一、引入依赖 二、配置数据库的连接信息 三、实现持久层代码 3.1 添加mapper接口 3.2 添加UserInfoXMLMapper.xml 3.3 增删改查操作 3.3.1 增(insert) 3.3.2 删(delete) 3.3.3 改(update) 3.3.4 查(select) 本篇内容仍然衔接上篇内容,使用的代码及案…...

读写RDS或RData等不同格式的文件,包括CSV和TXT、Excel的常见文件格式,和SPSS、SAS、Stata、Minitab等统计软件的数据文件
R语言是数据分析和科学计算的强大工具,其丰富的函数和包使得处理各种数据格式变得相对简单。在本文中,我们将详细介绍如何使用R语言的函数命令读取和写入不同格式的文件,包括RDS或RData格式文件、常见的文本文件(如CSV和TXT)、Excel文件,和和SPSS、SAS、Stata、Minitab等…...
视频支持格式)
Android 支持的媒体格式,(二)视频支持格式
视频支持格式: 格式编码器解码器具体说明文件类型 容器格式H.263是是对 H.263 的支持在 Android 7.0 及更高版本中并非必需• 3GPP (.3gp) • MPEG-4 (.mp4) • Matroska (.mkv)H.264 AVC Baseline Profile (BP)Android 3.0 及以上版本是 • 3GPP (.3gp) • MPEG-4…...

密码学原理精解【8】
文章目录 概率分布哈夫曼编码实现julia官方文档建议的变量命名规范:julia源码 熵一、信息熵的定义二、信息量的概念三、信息熵的计算步骤四、信息熵的性质五、应用举例 哈夫曼编码(Huffman Coding)基本原理编码过程特点应用具体过程1. 排序概…...
2024年钉钉杯大数据竞赛A题超详细解题思路+python代码手把手保姆级运行讲解视频+问题一代码分享
初赛A:烟草营销案例数据分析 AB题综合难度不大,难度可以视作0.4个国赛,题量可以看作0.35个国赛题量。适合于国赛前队伍练手,队伍内磨合。竞赛获奖率50%,八月底出成绩,参赛人数3000队左右。本文将为大家进行…...
unity2D游戏开发01项目搭建
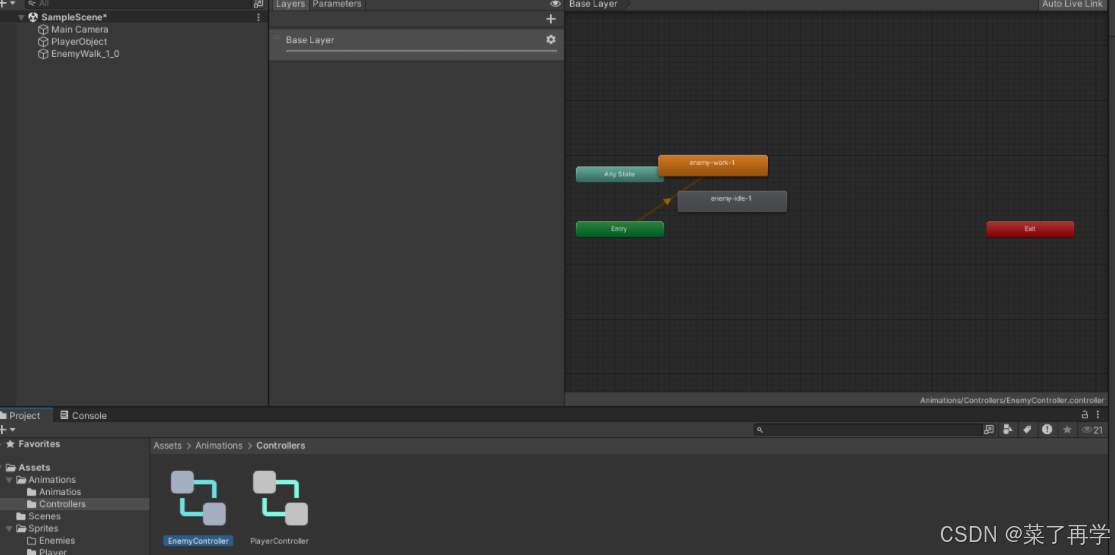
1新建项目 选择2d模板,设置项目名称和存储位置 在Hierarchy面板右击,create Empty 添加组件 在Project视图中右键新建文件夹 将图片资源拖进来(图片资源在我的下载里面) 点击Player 修改属性,修好如下 点击Sprite Editor 选择第二…...

删除的视频怎样才能恢复?详尽指南
在日常生活中,我们有时会不小心删除一些重要的视频文件,或者在整理存储空间时不慎丢失了珍贵的记忆片段。这时候,我们可以通过一些数据恢复工具和技巧,找回这些被删除的视频。本文将详细介绍几种常见且有效的视频恢复方法…...

LeetCode160 相交链表
前言 题目: 160. 相交链表 文档: 代码随想录——链表相交 编程语言: C 解题状态: 没思路… 思路 依旧是双指针法,很巧妙的方法,有点想不出来。 代码 先将两个链表末端对齐,然后两个指针齐头并…...

高性能响应式UI部件DevExtreme v24.1.4全新发布
DevExtreme拥有高性能的HTML5 / JavaScript小部件集合,使您可以利用现代Web开发堆栈(包括React,Angular,ASP.NET Core,jQuery,Knockout等)构建交互式的Web应用程序。从Angular和Reac,…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...
