【C++】:红黑树的应用 --- 封装map和set
点击跳转至文章:【C++】:红黑树深度剖析 — 手撕红黑树!
目录
- 前言
- 一,红黑树的改造
- 1. 红黑树的主体框架
- 2. 对红黑树节点结构的改造
- 3. 红黑树的迭代器
- 3.1 迭代器类
- 3.2 Begin() 和 End()
- 四,红黑树相关接口的改造
- 4.1 Find 函数的改造
- 4.2 Insert 函数的改造
- 五,红黑树改造的完整代码
- 六,set 的封装实现
- 七,map 的封装实现
前言
map 和 set 的底层本质上还是复用,通过对红黑树的改造,再分别套上一层 map 和 set 的 “壳子”,以达到 “一树二用” 的目的。
在改造红黑树的过程中,我大概归纳了以下几个需要重点解决的问题:
(1) 对红黑树节点的改造。关联式容器中存储的是<key, value>的键值对,K为key的类型,如果是 set 则是 K,如果是map,则为pair<K, V>。如何用一个节点结构控制两种类型,使用类模板参数T。
(2) 在插入操作时,如何完成数据的比较。由于我们的节点类型的泛型,如果是 set 则是 K,如果是map,则为pair<K, V>,而pair的比较是由 first 和 second 共同决定的,这显然不符合要求。因此插入数据时不能直接比较,要在 set 和 map 类中实现一个 KeyOfT 的仿函数,以便单独获取两个类型中的 key 数据。
(3) 在红黑树中实现普通迭代器和const迭代器,再套上 “壳子”。
(4) 关于 key 的修改问题。在STL库中,set 和 map 的 key 都是不能修改的,因为要符合二叉搜索树的特性,但是 map 中的 value 又是可以修改的。这个问题需要单独处理。
(5) 红黑树相关接口的改造。其中包括对 Find 和 Insert 函数的改造,特别是 Insert,因为在 map 里实现 operator[] 时需要依赖 Insert 函数。
说明:如果大家要自己动手实现封装,可以按照上面五个问题的流程进行实现。但是在本篇文章中由于展示等的原因,无法按照上面的步骤。
一,红黑树的改造
1. 红黑树的主体框架
(1) K 是给find,erase用的,T 是给节点,insert用的;
(2) KeyOfT 是由于下面需要比较,但是比较时不知道T的类型, set是key类型的比较,map是pair类型的比较,要统一变成key的比较。
template <class K, class T, class KeyOfT>
class RBTree
{typedef RBTreeNode<T> Node; //节点
public:typedef RBTreeIterator<T, T&, T*> Iterator; //普通迭代器typedef RBTreeIterator<T, const T&, const T*> ConstIterator; //const 迭代器//其他功能的实现……private:Node* _root = nullptr;
};2. 对红黑树节点结构的改造
//枚举颜色
enum Colour
{RED,BLACK
};//节点类
template <class T>
struct RBTreeNode
{T _data;RBTreeNode<T>* _left;RBTreeNode<T>* _right;RBTreeNode<T>* _parent;//pair<K, V> _kv;Colour _col;RBTreeNode(const T& data):_left(nullptr), _right(nullptr), _parent(nullptr), _data(data), _col(BLACK){}
};3. 红黑树的迭代器
3.1 迭代器类
//迭代器类
template <class T, class Ref, class Ptr>
struct RBTreeIterator
{typedef RBTreeNode<T> Node;typedef RBTreeIterator<T, Ref, Ptr> Self;Node* _node;RBTreeIterator(Node* node):_node(node){}bool operator!=(const Self& s){return s._node != _node;}Ref operator*(){return _node->_data;}Ptr operator->(){return &_node->_data;}//从局部的某一个过程考虑Self& operator++(){if (_node->_right){//右不为空,右子树的最左节点就是下一个访问的节点Node* leftMost = _node->_right;while (leftMost->_left)leftMost = leftMost->_left;_node = leftMost;}else{//右为空,代表当前节点所在的子树已经访问完了,下一个访问的节点是祖先//沿着到根节点的那个路径查找,孩子是父亲左的那个祖先节点就是下一个访问的节点Node* cur = _node;Node* parent = cur->_parent;//循环找祖先while (parent && cur == parent->_right){cur = parent;parent = parent->_parent;}_node = parent;}return *this;}
};
迭代器中最复杂的就是 operator++()的实现,它与原先的 vector/list 不同,红黑树的迭代器是要完成二叉树的中序遍历。
为了完成二叉树的中序遍历,我们需要从局部的某一过程考虑,就是假设 it 已经走到了某一节点,要找到下一个访问的节点,分为两种情况:
(1) 当前节点的右子树不为空:
如下图,假设 it 已经到达了13节点,说明此时13的左子树已经访问完了,右子树不为空,下一个要访问的节点就是右子树的最左节点15

(2) 当前节点的右子树为空:
如下图,假设 it 此时到达了15节点,它的右子树为空,下一个访问哪个节点呢?有些人单纯的认为是15的父亲17,其实是错误的。
那假设 it 到达6节点上呢,6的右为空,但是根据中序遍历的顺序,6的父亲1已经访问过了。

其实此时是要找当前节点的祖先,父亲也是祖先之一。
右为空,代表当前节点所在的子树已经访问完了,下一个访问的节点是祖先,是哪个祖先呢?沿着到根节点的那个路径查找,孩子是父亲左的那个祖先节点就是下一个访问的节点。
(a) 假设此时走到了15节点,下一个访问的节点是17,cur 是 parent 的左,parent 就是下一个要访问的那个祖先节点;

(b) 假设此时走到了6节点,下一个访问的节点是8,但是此时 cur 是 parent 的右,不满足条件,继续向上查找,cur = parent,parent = parent->_parent,这时 cur 在1,parent 在8,cur 是 parent 的左,parent 就是下一个要访问的那个祖先节点

3.2 Begin() 和 End()
//中序遍历,找树的最左节点
Iterator Begin()
{//Node* cur = _root;Node* leftMost = _root;while (leftMost->_left)leftMost = leftMost->_left;return Iterator(leftMost);
}Iterator End()
{return Iterator(nullptr);
}ConstIterator Begin()const
{//Node* cur = _root;Node* leftMost = _root;while (leftMost->_left)leftMost = leftMost->_left;return ConstIterator(leftMost);
}ConstIterator End()const
{return ConstIterator(nullptr);
}Iterator Find(const K& key)
{Node* cur = _root;while (cur){if (cur->_data > key)cur = cur->_left;else if (cur->_data < key)cur = cur->_right;elsereturn Iterator(cur);}return End();
}
四,红黑树相关接口的改造
4.1 Find 函数的改造
查找成功,返回查找到的那个节点的迭代器,查找失败,就返回 nullptr。
Iterator Find(const K& key)
{Node* cur = _root;while (cur){if (cur->_data > key)cur = cur->_left;else if (cur->_data < key)cur = cur->_right;elsereturn Iterator(cur);}return End();
}
4.2 Insert 函数的改造
map 里的 operator[] 需要依赖 Insert 的返回值
pair<Iterator, bool> Insert(const T& data)
{if (_root == nullptr){_root = new Node(data);return make_pair(Iterator(_root), true);}KeyOfT kot;Node* cur = _root;Node* parent = nullptr;while (cur){if (kot(cur->_data) > kot(data)){parent = cur;cur = cur->_left;}else if (kot(cur->_data) < kot(data)){parent = cur;cur = cur->_right;}elsereturn make_pair(Iterator(cur), false);}cur = new Node(data);Node* newnode = cur;//此处省略变色+旋转部分的代码……
五,红黑树改造的完整代码
说明:由于代码太长,影响展示效果,所以插入部分的 变色+旋转 的代码此处省略,和红黑树的基本一模一样,请前往【C++】:红黑树深度剖析 — 手撕红黑树!
RBTree.h
#include <iostream>
#include <assert.h>
using namespace std;//枚举颜色
enum Colour
{RED,BLACK
};//节点类
template <class T>
struct RBTreeNode
{T _data;RBTreeNode<T>* _left;RBTreeNode<T>* _right;RBTreeNode<T>* _parent;//pair<K, V> _kv;Colour _col;RBTreeNode(const T& data):_left(nullptr), _right(nullptr), _parent(nullptr), _data(data), _col(BLACK){}
};//迭代器类
template <class T, class Ref, class Ptr>
struct RBTreeIterator
{typedef RBTreeNode<T> Node;typedef RBTreeIterator<T, Ref, Ptr> Self;Node* _node;RBTreeIterator(Node* node):_node(node){}bool operator!=(const Self& s){return s._node != _node;}Ref operator*(){return _node->_data;}Ptr operator->(){return &_node->_data;}//从局部的某一个过程考虑Self& operator++(){if (_node->_right){//右不为空,右子树的最左节点就是下一个访问的节点Node* leftMost = _node->_right;while (leftMost->_left)leftMost = leftMost->_left;_node = leftMost;}else{//右为空,代表当前节点所在的子树已经访问完了,下一个访问的节点是祖先//沿着到根节点的那个路径查找,孩子是父亲左的那个祖先节点就是下一个访问的节点Node* cur = _node;Node* parent = cur->_parent;//循环找祖先while (parent && cur == parent->_right){cur = parent;parent = parent->_parent;}_node = parent;}return *this;}
};//K 是给find,erase用的,T 是给节点,插入用的
// KeyOfT 是由于下面需要比较,但是比较时不知道T的类型,
// set是key类型的比较,map是pair类型的比较,要统一变成key的比较template <class K, class T, class KeyOfT>
class RBTree
{typedef RBTreeNode<T> Node;
public:typedef RBTreeIterator<T, T&, T*> Iterator;typedef RBTreeIterator<T, const T&, const T*> ConstIterator;//中序遍历,找树的最左节点Iterator Begin(){//Node* cur = _root;Node* leftMost = _root;while (leftMost->_left)leftMost = leftMost->_left;return Iterator(leftMost);}Iterator End(){return Iterator(nullptr);}ConstIterator Begin()const{//Node* cur = _root;Node* leftMost = _root;while (leftMost->_left)leftMost = leftMost->_left;return ConstIterator(leftMost);}ConstIterator End()const{return ConstIterator(nullptr);}Iterator Find(const K& key){Node* cur = _root;while (cur){if (cur->_data > key)cur = cur->_left;else if (cur->_data < key)cur = cur->_right;elsereturn Iterator(cur);}return End();}pair<Iterator, bool> Insert(const T& data){if (_root == nullptr){_root = new Node(data);return make_pair(Iterator(_root), true);}KeyOfT kot;Node* cur = _root;Node* parent = nullptr;while (cur){if (kot(cur->_data) > kot(data)){parent = cur;cur = cur->_left;}else if (kot(cur->_data) < kot(data)){parent = cur;cur = cur->_right;}elsereturn make_pair(Iterator(cur), false);}cur = new Node(data);Node* newnode = cur;//新增节点,颜色为红色cur->_col = RED;//此处省略变色+旋转部分的代码……private:Node* _root = nullptr;};
六,set 的封装实现
set的底层为红黑树,因此只需在set内部封装一棵红黑树,即可将该容器实现出来。
为了解决 set 中 key 值不能修改的问题,在传给 RBTree 的第二个模板参数前加 const 即可。
MySet.h
#include "RBTree.h"namespace cc
{template<class K>class set{// 获取 set 里面的 keystruct SetOfT{const K& operator()(const K& key){return key;}};public:typedef typename RBTree<K, const K, SetOfT>::Iterator iterator;typedef typename RBTree<K, const K, SetOfT>::ConstIterator const_iterator;iterator begin(){return _t.Begin();}iterator end(){return _t.End();}const_iterator begin()const{return _t.Begin();}const_iterator end()const{return _t.End();}pair<iterator, bool> insert(const K& key){return _t.Insert(key);}iterator find(const K& key){return _t.Find(key);}private:RBTree<K, const K, SetOfT> _t;};
}//使用 const 迭代器
void Print(const cc::set<int>& s)
{auto it = s.begin();while (it != s.end()){cout << *it << " ";++it;}cout << endl;
}//测试代码
void Test_set()
{//int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };int a[] = { 16,3,7,11,9,26,18,14,15 };cc::set<int> s;for (auto e : a)s.insert(e);for (auto e : s)cout << e << " ";cout << endl;Print(s);
}

七,map 的封装实现
map的底层结构就是红黑树,因此在map中直接封装一棵红黑树,然后将其接口包装下即可。
map 中 pair 的 first 不能修改,second 可以修改,在 pair 的第一个参数前加 const 即可。
MyMap.h
#include "RBTree.h"namespace cc
{template<class K, class V>class map{//获取 pair 中的 keystruct MapOfT{const K& operator()(const pair<K, V>& kv){return kv.first;}};public:typedef typename RBTree<K, pair<const K, V>, MapOfT>::Iterator iterator;typedef typename RBTree<K, pair<const K, V>, MapOfT>::ConstIterator const_iterator;iterator begin(){return _t.Begin();}iterator end(){return _t.End();}const_iterator begin()const{return _t.Begin();}const_iterator end()const{return _t.End();}pair<iterator, bool> insert(const pair<K, V>& kv){return _t.Insert(kv);}iterator find(const K& key){return _t.Find(key);}//给一个key,返回value的引用V& operator[](const K& key){pair<iterator, bool> ret = insert(make_pair(key, V()));return ret.first->second;}private:RBTree<K, pair<const K,V>, MapOfT> _t;};
}//测试代码
void Test_map()
{cc::map<string, string> dict;dict.insert({ "left","左边" });dict.insert({ "right","右边" });dict.insert({ "insert","插入" });dict["left"] = "剩余,左边";cc::map<string, string>::iterator it = dict.begin();while (it != dict.end()){//it->first += 'x'; //errit->second += 'y'; //okcout << it->first << ":" << it->second << endl;++it;}cout << endl;
}
相关文章:

【C++】:红黑树的应用 --- 封装map和set
点击跳转至文章:【C】:红黑树深度剖析 — 手撕红黑树! 目录 前言一,红黑树的改造1. 红黑树的主体框架2. 对红黑树节点结构的改造3. 红黑树的迭代器3.1 迭代器类3.2 Begin() 和 End() 四,红黑树相关接口的改造4.1 Find…...

unity美术资源优化(资源冗余,主界面图集过多)
图片资源冗余: UPR unity的性能优化工具检查资源 1.检查纹理读/写标记 开启纹理资源的读/写标志会导致双倍的内存占用 检查Inspector -> Advanced -> Read/Write Enabled选项 2.检查纹理资源alpha通道 如果纹理的alpha通道全部为0,或者全部为2…...

【git】github中的Pull Request是什么
在 Git 中,"pull request"(简称 PR)是一种在分布式版本控制系统中使用的功能,特别是在使用 GitHub、GitLab、Bitbucket 等基于 Git 的代码托管平台时。Pull Request 允许开发者请求将他们的代码更改合并到另一个分支&am…...

gitlab查询分支API显示不全,只有20个问题
背景 gitlab查询分支API需要查询所有分支,且分支数量大于20,但目前调用接口返回的branch最多就显示了20个 解决方案 根据GitLab的文档,查询分支API默认最多返回20个分支。如果要一次性显示80个分支,可以使用分页参数来获取所有…...

vue3+vite 实现动态引入某个文件夹下的组件 - glob-import的使用
<template><div class"user-content"><HeaderTitle title"用户详情"></HeaderTitle><div class"main-content"><div><UserForm /></div><div><TableList></TableList></d…...

hhhhh
x torch.tensor([1.0,0.],[-1.,1.],requires_gradTrue) z x.pow(2).sum() z.backward() x.grad在这段代码中,我们利用 PyTorch 进行自动求梯度,下面详细解释代码的每一个部分及其在反向传播中的作用。同时,我们也将介绍函数对象和叶子节点的…...

扫雷小游戏纯后端版
package com.wind;import java.util.Random; import java.util.Scanner;public class ResultLei {static Random random new Random();public static void main(String[] args) {boolean end true;while (end) {System.out.println("请输入你选择的难度对应的数字&#…...
)
RuoYi-Vue-Plus(动态添加移除数据源)
一、添加数据 private final DynamicRoutingDataSource dynamicRoutingDataSource;private final DefaultDataSourceCreator dataSourceCreator;//添加一个dynamic的数据源@GetMapping("createDynamic")public void createDynamic() {DataSourceProperty property =…...
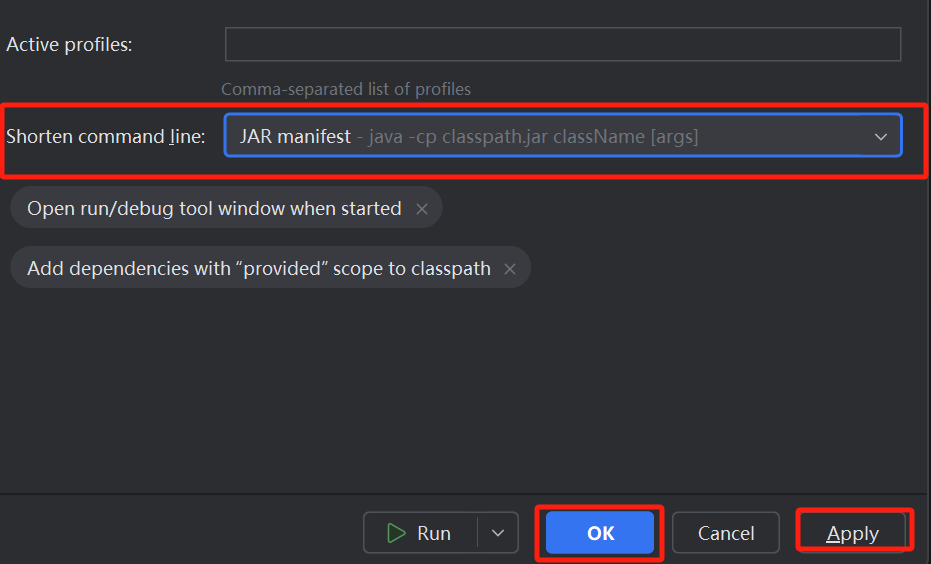
idea启动项目报:the command line via JAR manifest or via a classpath file and rerun.
解决方案 1.打开Edit Configurations,进去编辑,如下: 笔记配置 2.选择Modfiy options,点击Shorten command line 3.在新增的Shorten command line选项中选择JAR manifest或classpath file 4.点击保存后即可...

vue3 + ts中有哪些类型是由vue3提供的?
在 Vue 3 中结合 TypeScript 使用时,Vue 提供了一系列的类型帮助函数和接口,这些类型用于增强 TypeScript 的集成和提供类型安全。以下是一些由 Vue 3 提供的常用 TypeScript 类型: RefType: 用于标注一个 ref 返回的响应式引用类型。Reacti…...

【Linux】远程连接Linux虚拟机(MobaXterm)
【Linux】远程连接Linux虚拟机(MobaXterm) 零、原因 有时候我们在虚拟机中操作Linux不太方便,比如不能复制粘贴,不能传文件等等,我们在主机上使用远程连接软件远程连接Linux虚拟机后可以解决上面的问题。 壹、软件下…...

LeetCode Hot100 生成特殊数字的最少操作
给你一个下标从 0 开始的字符串 num ,表示一个非负整数。 在一次操作中,您可以选择 num 的任意一位数字并将其删除。请注意,如果你删除 num 中的所有数字,则 num 变为 0。 返回最少需要多少次操作可以使 num 变成特殊数字。 如…...

Spring MVC 应用分层
1. 类名使⽤⼤驼峰⻛格,但以下情形例外:DO/BO/DTO/VO/AO 2. ⽅法名、参数名、成员变量、局部变量统⼀使⽤⼩驼峰⻛格 3. 包名统⼀使⽤⼩写,点分隔符之间有且仅有⼀个⾃然语义的英语单词. 常⻅命名命名⻛格介绍 ⼤驼峰: 所有单词⾸字⺟…...

QT--进程
一、进程QProcess QProcess 用于启动和控制外部进程,管理其输入输出流。 使用方法 start():启动一个新进程。setStandardInputFile():将文件作为标准输入。将进程的标准输入(stdin)重定向到指定的文件。换句话说&am…...

凸优化笔记-基本概念
原文 文章目录 最小二乘问题 仿射affine hullaffine dimension 凸集锥集超平面和半空间单纯形整半定锥保凸性的操作透视函数 凸函数的条件1阶判定条件2阶判定条件 Epigraph 外图 m i n i m i z e f 0 ( x ) minimize\ \ \ f_0(x) minimize f0(x) s u b j e c t t o f i ( …...

1858. 数组查找及替换
问题描述 给定某整数数组和某一整数 b 。 要求删除数组中可以被 b 整除的所有元素,同时将该数组各元素按从小到大排序。如果数组元素数值在 𝐴‘ 到 Z 的 ASCII 之间,替换为对应字母。 元素个数不超过 100,𝑏 在 1 …...
计算机视觉与面部识别:技术、应用与未来发展
引言 在当今数字化时代,计算机视觉技术迅速发展,成为人工智能领域的一个重要分支。计算机视觉旨在让机器理解和解释视觉信息,模拟人类的视觉系统。它在各行各业中发挥着重要作用,从自动驾驶汽车到智能监控系统,再到医疗…...

懒人精灵安卓版纯本地离线文字识别插件
目的 懒人精灵是一款可以模拟鼠标和键盘操作的自动化工具。它可以帮助用户自动完成一些重复的、繁琐的任务,节省大量人工操作的时间。懒人精灵也包含图色功能,识别屏幕上的图像,根据图像的变化自动执行相应的操作。本篇文章主要讲解下更优秀的…...

在线教育数仓项目(数据采集部分1)
文章目录 数据仓库概念项目需求及架构设计项目需求分析系统数据流程设计框架版本选型集群规模估算集群资源规划设计 数据生成模块目标数据页面事件曝光启动播放错误 数据埋点主流埋点方式(了解)埋点数据上报时机埋点数据日志结构 服务器和JDK准备服务器准…...

帕金森病(PD)诊断:三种基于语音的深度学习方法
帕金森病(Parkinson’s disease, PD)是世界上第二大流行的神经退行性疾病,全球影响着超过1000万人,仅次于阿尔茨海默症。人们通常在65岁左右被诊断出患有此病。PD的一些症状包括震颤、肌肉僵硬和运动迟缓。这些症状往往出现在较晚…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

适应性Java用于现代 API:REST、GraphQL 和事件驱动
在快速发展的软件开发领域,REST、GraphQL 和事件驱动架构等新的 API 标准对于构建可扩展、高效的系统至关重要。Java 在现代 API 方面以其在企业应用中的稳定性而闻名,不断适应这些现代范式的需求。随着不断发展的生态系统,Java 在现代 API 方…...
