智能优化算法之灰狼优化算法(GWO)

智能优化算法是一类基于自然界中生物、物理或社会现象的优化技术。这些算法通过模拟自然界中的一些智能行为,如遗传学、蚁群觅食、粒子群体运动等,来解决复杂的优化问题。智能优化算法广泛应用于各种工程和科学领域,因其具有全局搜索能力、鲁棒性强以及易于实现等优点。
灰狼优化算法(GWO)

灰狼优化算法(Grey Wolf Optimizer, GWO)是一种新兴的智能优化算法,灵感来源于灰狼的捕猎行为。该算法由Seyedali Mirjalili等人在2014年提出,模拟了灰狼的社会层次结构和合作狩猎的策略。
GWO算法自2014年提出以来,受到了广泛关注和研究。它不仅在学术界被广泛研究和引用,而且在工程优化、机器学习、图像处理等多个领域得到了成功应用。GWO最初只是作者在研究其他优化算法时的灵感,但最终却发展成为一个独立且强大的优化工具。
灰狼被认为是顶级捕食者,位于食物链的顶端。灰狼喜欢群居,每群平均有5至12只灰狼。如附图所示,群体中的所有个体都具有非常严格的社会支配等级。
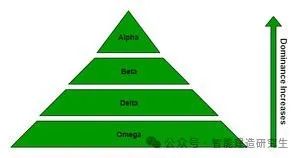
图2 灰狼的社会等级*
Alpha (α) 狼被视为狼群中的主导狼,狼群成员必须服从它的命令。
Beta (β) 是从属狼,帮助 Alpha 做出决策,被视为成为 Alpha 的最佳候选人。
Delta(δ)狼必须服从 Alpha 和 Beta,但它们主宰 Omega。δ 狼有不同的类别,如侦察兵、哨兵、长老、猎人、看守者等。
Omega (ω) 狼被视为狼群中的替罪羊,是狼群中最不重要的个体,只能在最后才被允许进食。
灰狼狩猎的主要阶段:
-
追踪、追逐并接近猎物。
-
追逐、包围、骚扰猎物,直到其停止移动。
-
向猎物发起攻击。
通过数学建模来设计灰狼的社会等级和狩猎行为,以设计 GWO。
数学模型与算法
社会等级
-
最适合的解决方案是Alpha狼(α)
-
第二最佳解决方案是 Beta 狼(β)
-
第三最佳解决方案是 Delta 狼(δ)
-
其余候选解决方案为 Omega 狼(ω)
数学模型
灰狼优化算法的数学模型描述了某个目标函的优化方法(寻找最优值,即猎物)
![]()
(1)需要优化的函数
其中是维向量。首先,随机生成个解
![]()
(2)初始化解决方案
其中,对应于特定维度分量,从和向量中返回随机值,这些向量是所有的下限和上限。根据狼的等级制度,三个最佳(达到最低值)解决方案α、β和δ(通常为)分别映射到 α、β 和 δ 狼。我们假设领导者对猎物的位置有最丰富的经验,因此他们会指挥其他狼。猎物位置(由领导者确定)与狼群其他成员之间的距离计算为
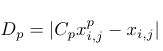
(3)距离计算
其中是每个领导者的位置分量(与猎物位置大致相同),是每个解决方案的分量,是 来自 [0, 2] 的特殊随机参数。此参数指定“随机性”——在猎物邻域中搜索。在计算与领导者相关的三个距离后,我们应该计算他们的新位置,如下所示(这里的与分量不同,它只是另一个变量)
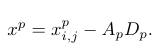
(4)领导职位
最后一个等式意味着我们通过距离值乘以某个随机因子来接近猎物。值和是算法的关键参数。第一个等式增加了特殊的随机性,即如果(探索阶段),它允许狼通过偏离
来寻找更好的猎物。否则,如果,那么狼的新位置可以位于先前位置和猎物位置之间的任何区域。这意味着狼开始攻击猎物。在迭代过程中,该值通过以下公式进行更改
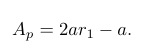
(5)计算
这里是从 2(初始值)下降到 0 的递减(通常是线性的)因子
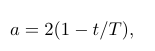
(6)递减因子计算
其中是当前迭代次数,是预先定义的总迭代次数,是 中的随机值。
参数(也是 中的随机值*)
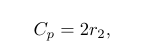
(7)C_p计算
可以看作是狼在野外接近猎物时遇到的障碍物的影响。在自然界中,这些障碍物通常表现为狼狩猎路线上的障碍物,有效地阻碍了它们迅速轻松地接近猎物的能力。换句话说,它可能会随机为猎物分配一个难度或距离等级,使狼要么更难接近猎物,要么更难接近猎物,或者相反,更容易接近猎物。迫使狼进行探索而不是开发,并有助于避免局部最小值。
生成值后,可以计算出狼的新位置,作为的平均值
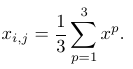
(8)计算新解
所描述的过程如下所示。
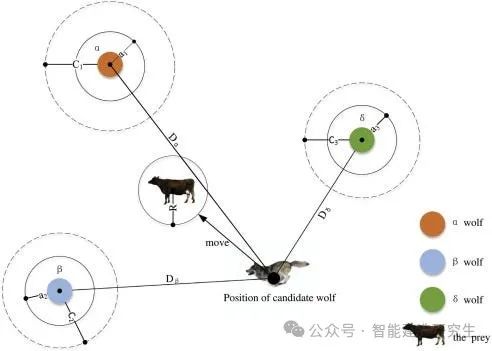
img
算法详见:https://doi.org/10.1016/j.knosys.2019.01.018IF: 7.2 Q1
GWO 算法的伪代码
1. 初始化解的数量 N、总迭代次数T和边界向量 x^{ub}, x^{lb};
2. 使用公式 (2) 随机生成 N 个解;
3. 确定三个最佳解 (领导者) X^p,p=1..3;
3. 对于 t=1..N(迭代循环):
4. 通过 (6) 计算值 a;
5. 对于每个第 i 个解:
6. 对于每个第 j 个维度:
7. 使用 (5) 和 (7) 计算 A_p 和 C_p;
8. 通过 (3) 计算三个距离 D_p;
9. 通过 (4) 计算三个 x^p;
10. 通过 (8) 生成新的解分量 x^{new}_{i,j};
11. 如果 x^{new}_{i,j} 位于 x^{ub} 或 x^{lb} 之外,则将相应的 x^{ub} 或 x^{lb} 分配给 x^{new}_{i,j};
12. 如果 f(x^{new}_i)>f(x_i),则丢弃 x^{new}_i,保留前一个x_i,即 x^{new}_i = x_i (与 x_i(t+1) = x_i(t) 相同);
13. 更新三个最佳解(领导者)X^p,p=1..3。
详情参见:https://www.sciencedirect.com/science/article/pii/S0965997813001853
应用领域和场景
灰狼优化算法因其简单、高效和全局搜索能力强,广泛应用于:
-
多层感知器的训练算法
-
训练 q-高斯径向基函数链接网络
-
经济调度问题
-
特征子集选择
-
电力系统电网
-
进化种群动态
-
优化关键值
网址:https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0287405
参考资料:https://medium.com/@deneb.acyg/grey-wolf-optimizer-in-c-part-1-intuition-232be414f4ad
https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0287405
https://transpireonline.blog/2019/08/09/behavior-of-grey-wolf-optimization-gwo-algorithm-using-meta-heuristics-method/
基于Python的可视化算法实例
下面是一个基于Python实现的GWO算法实例,并通过可视化展示其优化过程:
import numpy as np # 导入NumPy库,用于数值计算
import matplotlib.pyplot as plt # 导入matplotlib的pyplot模块,用于绘图# 定义一个灰狼优化器类
class GreyWolfOptimizer:# 初始化方法def __init__(self, objective_function, dimension, lower_bound, upper_bound, population_size, iterations):self.objective_function = objective_function # 目标函数self.dimension = dimension # 问题的维度self.lower_bound = np.array(lower_bound) # 参数的下界self.upper_bound = np.array(upper_bound) # 参数的上界self.population_size = population_size # 群体大小self.iterations = iterations # 迭代次数# 初始化种群self.population = np.random.rand(population_size, dimension) * (self.upper_bound - self.lower_bound) + self.lower_boundself.alpha = self.population[0] # 初始化alpha狼self.beta = self.population[1] # 初始化beta狼self.delta = self.population[2] # 初始化delta狼# 优化方法def optimize(self):for _ in range(self.iterations): # 对每一代进行迭代for i in range(self.population_size): # 遍历种群中的每一个个体# 计算每个维度的系数A, C和距离DA = 2 * np.random.rand(self.dimension) - 1C = 2 * np.random.rand()D_alpha = np.abs(C * self.alpha - self.population[i])X1 = self.alpha - A * D_alphaA = 2 * np.random.rand(self.dimension) - 1C = 2 * np.random.rand()D_beta = np.abs(C * self.beta - self.population[i])X2 = self.beta - A * D_betaA = 2 * np.random.rand(self.dimension) - 1C = 2 * np.random.rand()D_delta = np.abs(C * self.delta - self.population[i])X3 = self.delta - A * D_deltaself.population[i] = (X1 + X2 + X3) / 3 # 更新个体位置# 计算种群的适应度fitness = np.array([self.objective_function(ind) for ind in self.population])# 根据适应度排序并更新alpha, beta, deltabest_indexes = np.argsort(fitness)[:3]self.alpha, self.beta, self.delta = self.population[best_indexes]# 定义电网优化的目标函数
def power_system_optimization(x):return np.sum(x**2) # 返回所有参数的平方和# 初始化优化器参数
dimension = 5
lower_bound = [0]*dimension
upper_bound = [100]*dimension
population_size = 30
iterations = 50# 创建灰狼优化器实例
gwo = GreyWolfOptimizer(power_system_optimization, dimension, lower_bound, upper_bound, population_size, iterations)
gwo.optimize() # 进行优化# 可视化优化过程中Alpha, Beta, Delta的变化
plt.plot(gwo.alpha, label='Alpha')
plt.plot(gwo.beta, label='Beta')
plt.plot(gwo.delta, label='Delta')
plt.xlabel('Iteration')
plt.ylabel('Value')
plt.legend()
plt.title('GWO Optimization Process')
plt.show() # 显示图表
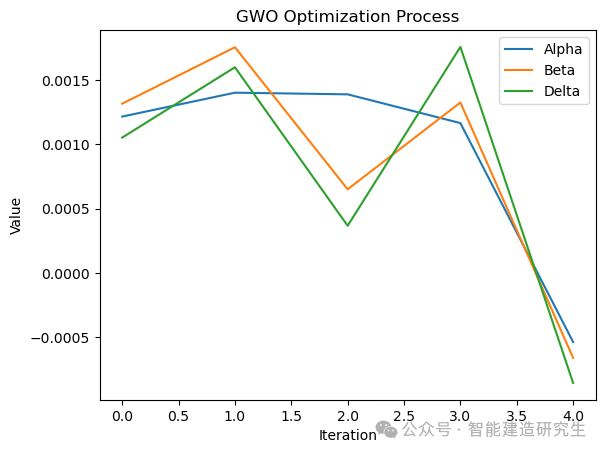
在上面的示例中,GWO算法被用于优化一个简化的电力系统模型,其中目标函数定义为所有变量的平方和,代表了一个假设的优化目标。代码初始化一个包含随机值的种群,然后通过迭代过程不断更新种群中个体的位置,以寻找最小化目标函数的解。这个过程中,算法更新了三个最优解,即 Alpha、Beta 和 Delta,它们代表了种群中的最优个体。
以上内容总结自网络,如有帮助欢迎关注与转发,我们下次再见!
相关文章:

智能优化算法之灰狼优化算法(GWO)
智能优化算法是一类基于自然界中生物、物理或社会现象的优化技术。这些算法通过模拟自然界中的一些智能行为,如遗传学、蚁群觅食、粒子群体运动等,来解决复杂的优化问题。智能优化算法广泛应用于各种工程和科学领域,因其具有全局搜索能力、鲁…...

昇思25天学习打卡营第17天|计算机视觉
昇思25天学习打卡营第17天 文章目录 昇思25天学习打卡营第17天ShuffleNet图像分类ShuffleNet网络介绍模型架构Pointwise Group ConvolutionChannel ShuffleShuffleNet模块构建ShuffleNet网络 模型训练和评估训练集准备与加载模型训练模型评估模型预测 打卡记录 ShuffleNet图像分…...
-MFC-C/C++ - 键鼠操作)
Windows图形界面(GUI)-MFC-C/C++ - 键鼠操作
公开视频 -> 链接点击跳转公开课程博客首页 -> 链接点击跳转博客主页 目录 MFC鼠标 派发流程 鼠标消息(客户区) 鼠标消息(非客户) 坐标处理 客户区 非客户 坐标转换 示例代码 MFC键盘 击键消息 虚拟键代码 键状态 MFC鼠标 派发流程 消息捕获&#…...

Angular 18.2.0 的新功能增强和创新
一.Angular 增强功能 Angular 是一个以支持开发强大的 Web 应用程序而闻名的平台,最近发布了 18.2.0 版本。此更新带来了许多新功能和改进,进一步增强了其功能和开发人员体验。在本文中,我们将深入探讨 Angular 18.2.0 为开发人员社区提供的…...

matlab 小数取余 rem 和 mod有 bug
目录 前言Matlab取余函数1 mod 函数1.1 命令行输入1.2 命令行输出 2 rem 函数2.1 命令行输入2.2 命令行输出 分析原因注意 前言 在 Matlab 代码中mod(0.11, 0.1) < 0.01 判断为真,mod(1.11, 0.1) < 0.01判断为假,导致出现意料外的结果。 结果发现…...

Avalonia中的数据模板
文章目录 1. 介绍和概述什么是数据模板:数据模板的用途:2. 定义数据模板在XAML中定义数据模板:在代码中定义数据模板:3. 使用数据模板在控件中使用数据模板:数据模板选择器:定义数据模板选择器:在XAML中使用数据模板选择器:4. 复杂数据模板使用嵌套数据模板:使用模板绑…...

Sqlmap中文使用手册 - Techniques模块参数使用
目录 1. Techniques模块的帮助文档2. 各个参数的介绍2.1 --techniqueTECH2.2 --time-secTIMESEC2.3 --union-colsUCOLS2.4 --union-charUCHAR2.5 --union-fromUFROM2.6 --dns-domainDNS2.7 --second-urlSEC2.8 --second-reqSEC 1. Techniques模块的帮助文档 Techniques:These o…...
科普文:kubernets原理
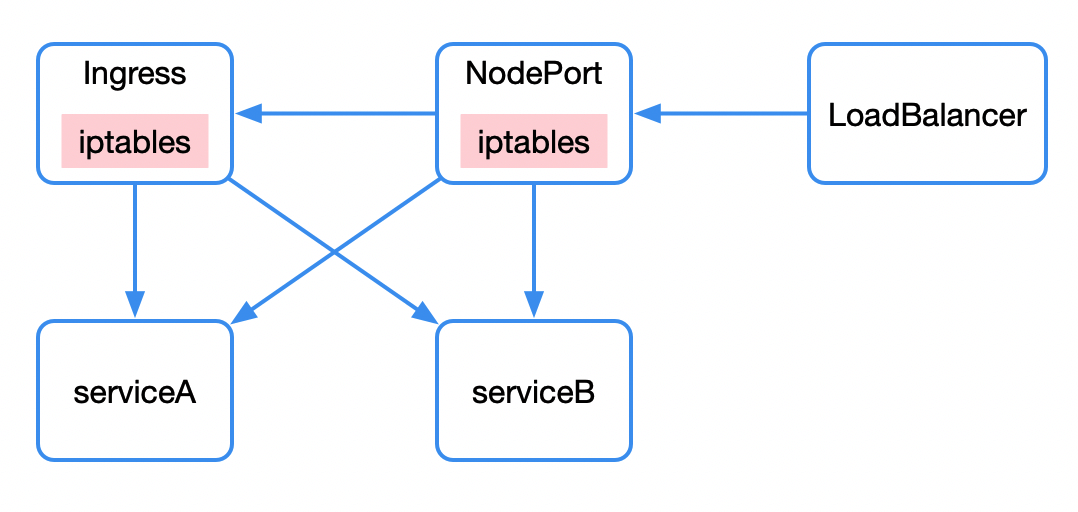
kubernetes 已经成为容器编排领域的王者,它是基于容器的集群编排引擎,具备扩展集群、滚动升级回滚、弹性伸缩、自动治愈、服务发现等多种特性能力。 本文将带着大家快速了解 kubernetes ,了解我们谈论 kubernetes 都是在谈论什么。 一、背…...

GO-学习-02-常量
常量是不变的 const package main import "fmt"func main() {//常量定义时必须赋值const pi 3.1415926const e 2.718//一次声明多个常量const(a 1b 2c "ihan")const(n1 100n2n3)//n2,n3也是100 同时声明多个常量时,如果省略了值则表示和…...

Vue系列面试题
大家好,我是有用就扩散,有用就点赞。 1.Vue中组件间有哪些通信方式? 父子组件通信: (1)props | $emit (接收父组件数据 | 传数据给父组件) (2)ref | $refs&a…...

等级保护 总结2
网络安全等级保护解决方案的主打产品: HiSec Insight安全态势感知系统、 FireHunter6000沙箱、 SecoManager安全控制器、 HiSecEngine USG系列防火墙和HiSecEngine AntiDDoS防御系统。 华为HiSec Insight安全态势感知系统是基于商用大数据平台FusionInsight的A…...

关于Redis(热点数据缓存,分布式锁,缓存安全(穿透,击穿,雪崩));
热点数据缓存: 为了把一些经常访问的数据,放入缓存中以减少对数据库的访问频率。从而减少数据库的压力,提高程序的性能。【内存中存储】成为缓存; 缓存适合存放的数据: 查询频率高且修改频率低 数据安全性低 作为缓存的组件: redis组件 memory组件 e…...

【北京迅为】《i.MX8MM嵌入式Linux开发指南》-第三篇 嵌入式Linux驱动开发篇-第四十七章 字符设备和杂项设备总结回顾
i.MX8MM处理器采用了先进的14LPCFinFET工艺,提供更快的速度和更高的电源效率;四核Cortex-A53,单核Cortex-M4,多达五个内核 ,主频高达1.8GHz,2G DDR4内存、8G EMMC存储。千兆工业级以太网、MIPI-DSI、USB HOST、WIFI/BT…...

C#初级——枚举
枚举 枚举是一组命名整型常量。 enum 枚举名字 { 常量1, 常量2, …… 常量n }; 枚举的常量是由 , 分隔的列表。并且,在这个整型常量列表中,通常默认第一位枚举符号的值为0,此后的枚举符号的值都比前一位大1。 在将枚举赋值给 int 类型的…...

Linux 动静态库
一、动静态库 1、库的理解 库其实是给我们提供方法的实现,如上面的对于printf函数的实现就是在库中实现的,而这个库也就是c标准库,本质也是文件,也有对应的路径 2、区别 静态库是指编译链接时,把库文件的代码全部加入…...
微信小游戏之 三消(一)
首先设定一下 单个 方块 cell 类: 类定义和属性 init 方法 用于初始化方块,接收游戏实例、数据、宽度、道具类型和位置。 onWarning 方法 设置警告精灵的帧,并播放闪烁动作,用于显示方块的警告状态。 grow 方法 根据传入的方向…...

软件测试---Linux
Linux命令使用:为了将来工作中与服务器设备进行交互而准备的技能(远程连接/命令的使用)数据库的使用:MySQL,除了查询动作需要重点掌握以外,其他操作了解即可什么是虚拟机 通过虚拟化技术,在电脑…...

数据库之数据表基本操作
目录 一、创建数据表 1.创建表的语法形式 2.使用SQL语句设置约束条件 1.设置主键约束 2.设置自增约束 3.设置非空约束 4.设置唯一性约束 5.设置无符号约束 6.设置默认约束 7.设置外键约束 8.设置表的存储引擎 二、查看表结构 1.查看表基本结构 2.查看建表语句 三…...

利用OSMnx求路网最短路径并可视化(二)
书接上回,为了增加多路径的可视化效果和坐标匹配最近点来实现最短路可视化,我们使用图形化工具matplotlib结合OSMnx的绘图功能来展示整个路网图,并特别高亮显示计算出的最短路径。 多起终点最短路路径并计算距离和时间 完整代码#运行环境 P…...
及其Python和MATLAB实现)
双向门控循环神经网络(BiGRU)及其Python和MATLAB实现
BiGRU是一种常用的深度学习模型,用于处理序列数据的建模和预测。它是基于GRU(Gated Recurrent Unit)模型的改进版本,通过引入更多的隐藏层和增加网络的宽度,能够更好地捕捉复杂的序列数据中的模式。 背景:…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...
