为什么样本方差(sample variance)的分母是 n-1?
样本均值与样本方差的定义
首先来看一下均值,方差,样本均值与样本方差的定义
总体均值的定义:
μ = 1 n ∑ i = 1 n X i \mu=\frac{1}{n}\sum_{i=1}^{n} X_i μ=n1i=1∑nXi
也就是将总体中所有的样本值加总除以个数,也可以叫做总体的数学期望或简称期望
总体方差的定义:
σ 2 = 1 n ∑ i = 1 n ( X i − μ ) 2 \sigma ^2=\frac {1}{n}\sum_{i=1}^{n} (X_i-\mu)^2 σ2=n1i=1∑n(Xi−μ)2
总体中全部样本各数值与总体均值差的平方和的平均数,用来衡量随机变量或一组数据离散程度的度量。
在实际应用中,我们一般是拿不到总体的均值与总体的方差,只能通过抽样得到的样本均值与样本方差来估计总体的均值与方差。于是我们就得到了样本均值和样本方差:
样本均值的定义
X ˉ = 1 n ∑ i = 1 n X i \bar {X}=\frac{1}{n}\sum_{i=1}^{n} X_i Xˉ=n1i=1∑nXi
样本方差的定义
S 2 = 1 n − 1 ∑ i = 1 n ( X i − X ˉ ) 2 S^2=\frac{1}{n-1} \sum_{i=1}^{n} (X_i - \bar X)^2 S2=n−11i=1∑n(Xi−Xˉ)2
对比总体方差的公式,样本方差的公式的系数为什么变为了 1 n − 1 \frac{1}{n-1} n−11?
通俗理解-自由度
一个比较通俗的的理解就是自由度,可以理解为对应的独立信息量。样本均值和样本方差就是抽样后把所有的独立的信息量(这里的独立的信息量就是数值,包含了均值和方差的信息)平均得到,在计算样本方差时用 X ˉ \bar X Xˉ替代了总体均值 μ \mu μ,自由度减少了一个。
假设只采样了两个样本 X 1 , X 2 X_1,X_2 X1,X2,这其中的信息量是多少呢?方差是计算样本之间的偏离程度,所以一个独立有效的信息量就是这个数值减去均值。在计算方差时分子有两项: ( X 1 − X ˉ ) 2 (X_1-\bar X)^2 (X1−Xˉ)2 和 ( X 2 − X ˉ ) 2 (X_2-\bar X)^2 (X2−Xˉ)2 . 要算第一个样本的偏离程度,毋庸置疑只能老老实实算 ( X 1 − X ˉ ) (X_1-\bar X) (X1−Xˉ);但是,第二个样本呢?计算 ( X 2 − X ˉ ) (X_2-\bar X) (X2−Xˉ) 吗?其实还有另外一种方法,因为 X ˉ = X 1 + X 2 2 \bar X=\frac{X_1+X_2}{2} Xˉ=2X1+X2, X 1 X_1 X1 和 X 2 X_2 X2 其实是对于 X ˉ \bar X Xˉ对称的。所以其实 ( X 2 − X ˉ ) = ( 2 X ˉ − X 1 − X ˉ ) = − ( X 1 − X ˉ ) (X_2-\bar X)=(2\bar X-X_1-\bar X)=-(X_1-\bar X) (X2−Xˉ)=(2Xˉ−X1−Xˉ)=−(X1−Xˉ)。也就是我们在用样本均值 X ˉ \bar X Xˉ替代总体均值后,只要 X 1 X_1 X1确定了之后, X 2 X_2 X2是可以根据 X 1 X_1 X1推出来具体数值的,实际能够有效提供样本到 X ˉ \bar X Xˉ的偏移量的信息数只有一条 X 1 X_1 X1。
我们对这种现象可以有一个表述:就是 ( X 2 − X ˉ ) (X_2-\bar X) (X2−Xˉ) 是不自由的,因为从之前的式子可以推出它。当然,对称地,我们也可以说 ( X 1 − X ˉ ) (X_1-\bar X) (X1−Xˉ)是不自由的。总之,这两个式子当中,只有一个是自由的,所以我们称这两个式子的自由度为 1.所以在两个样本求方差的时候要除1,应为实际应用到方差计算种的只有 ( X 1 − X ˉ ) (X_1-\bar X) (X1−Xˉ)这一个有效信息。
同样,将样本数增加至三个,当有两个样本 X 1 , X 2 X_1,X_2 X1,X2并且知道 X ˉ \bar X Xˉ的情况下,我们就可以推出第三个样本 X 3 X_3 X3的值,对应的自由度为 2.
以此类推,当我们有 n n n个样本的时候,其自由度为 n − 1 n - 1 n−1.也就是说,当我们有 n n n 个样本的时候,我们虽然看起来在分子上做了 n n n 个减法,但实际上我们只算出了 n − 1 n - 1 n−1 个偏差量。因此,做平均的时候,要除以的分母就是 n − 1 n - 1 n−1
但是,为什么 n 个减法做完,自由度只有 n - 1?是谁从中搞鬼,偷走了一个自由度?答案很简单,是 X ˉ \bar X Xˉ 。注意在总体方差中,隐含的分布均值是 μ \mu μ ,这个均值是知道了总体的分布后计算出来的,而在样本方差中 μ \mu μ 是未知的,所以在估计方差之前,我们会需要先找一个 μ \mu μ 的代替,也就是 X ˉ \bar X Xˉ ,而 X ˉ \bar X Xˉ是根据样本算出来的. 也就是说,在用 X ˉ \bar X Xˉ 代替 μ \mu μ 的过程中,我们损失了一个自由度。
那么,如果问题的背景变了,我们知道隐含的分布均值 μ \mu μ ,只是不知道 σ 2 \sigma^2 σ2 ,那我们该如何估计 σ 2 \sigma^2 σ2?这种情况下求方差就变成了符合直觉的 ( X 1 − μ ) 2 + ( X 2 − μ ) 2 + ⋯ + ( X n − μ ) 2 n \frac{(X_1-\mu)^2+(X_2-\mu)^2+\dots+(X_n-\mu)^2}{n} n(X1−μ)2+(X2−μ)2+⋯+(Xn−μ)2。
严密推导过程
估计量的评选标准
当我们用抽样的方法去估计总体时,总是希望每次抽样的结果尽可能的靠近实际的总体评估量,同时抽取的样本越多时越接近实际的总体评估量。对于评估量的好坏有如下三个评价指标
无偏性
设 θ \theta θ是总体的未知参数, X 1 , X 2 , . . . . . X n X_1,X_2,.....X_n X1,X2,.....Xn是总体的一个样本, θ ^ \widehat \theta θ 是参数的一个估计量,若
E ( θ ^ ) = θ E(\widehat \theta)=\theta E(θ )=θ
则称 θ ^ \widehat \theta θ 是 θ \theta θ的一个无偏估计量
无偏性简单来说就是取样后得到的估计量 θ ^ \widehat \theta θ 的期望就等于总体的估计量。
考虑如下一个打靶的例子。如果有一个射击高手打靶,那么结果总会在靶心附近(总体期望 θ \theta θ),那么我们一般会通过打靶结果(也就是样本 θ ^ \widehat \theta θ )认为这是一个熟练的射击手,对于多次的打靶结果我们对其打靶结果的期望是靶心( E ( θ ^ ) = θ E(\widehat \theta)=\theta E(θ )=θ),也就是无偏的。
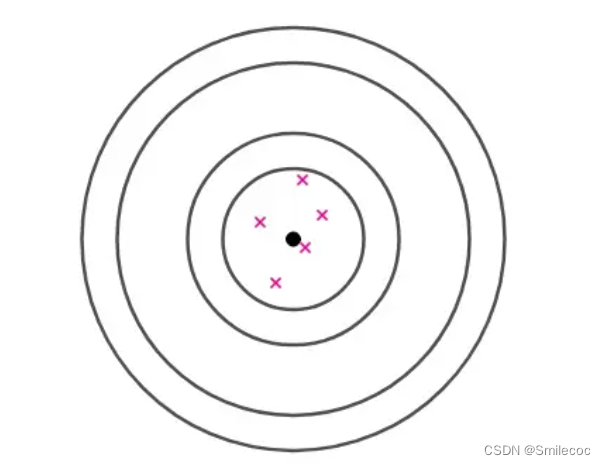
但如果出现了如下这种结果,通过这些样本我们就会猜测集中在一点附近可能是一个射击高手,这个偏差可能是由于瞄准镜歪了这种导致的呢
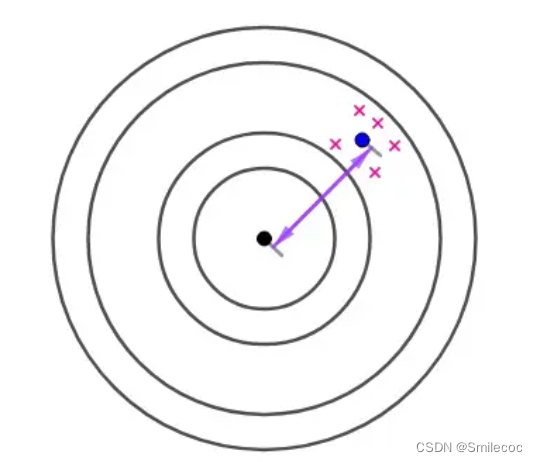
对于这种稳定影响结果的因素导致的偏差称为系统偏差,也就是 E ( θ ^ ) − θ E(\widehat \theta)-\theta E(θ )−θ。无偏估计的实际意义就是无系统偏差。很明显无偏估计更接近实际的总体统计量
有效性
若 θ ^ 1 {\widehat \theta}_1 θ 1和 θ ^ 2 {\widehat \theta}_2 θ 2都是样本 X 1 , X 2 , . . . . . X n X_1,X_2,.....X_n X1,X2,.....Xn的无偏估计量,若对于任意取值范围里有 D ( θ ^ 1 ) ≤ D ( θ ^ 2 ) D({\widehat \theta}_1) \le D({\widehat \theta}_2) D(θ 1)≤D(θ 2),
则 θ ^ 1 {\widehat \theta}_1 θ 1比 θ ^ 2 {\widehat \theta}_2 θ 2更加有效。
有效性就是同样无偏的估计量,更集中,方差更小的估计量更好
接着考虑如下打靶结果,虽然期望都是靶心,但是很明显后面的结果更加集中,相应的评估效果也会更好
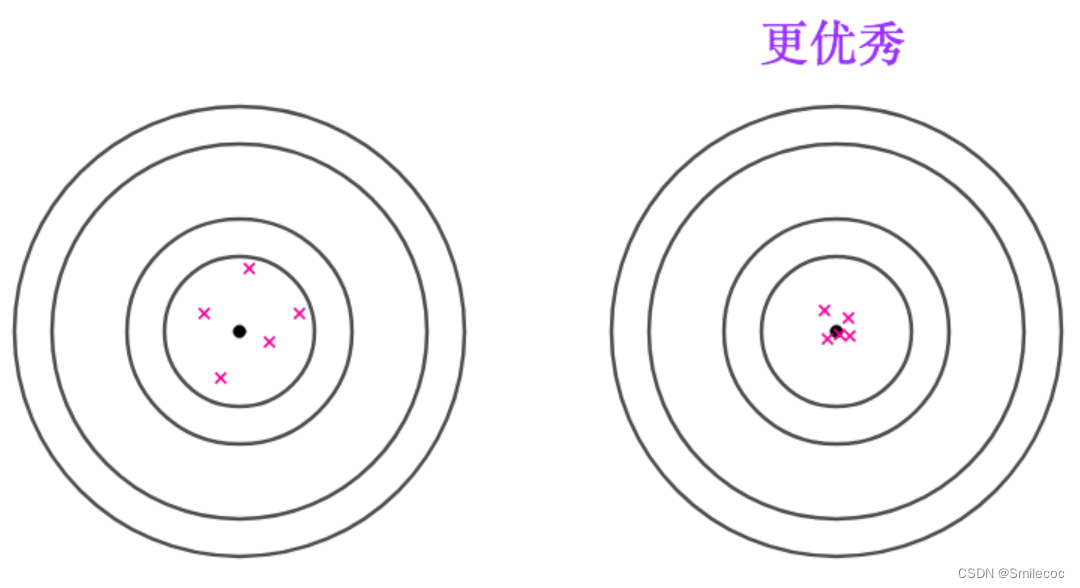
相合性
之前的无偏性和一致性都是在样本容量固定为n的情况下讨论的,而如果样本容量越来越多时,一个估计量能稳定于待估的参数真值
相合性大样本条件下,估计值等于实际值.对于任意 θ > 0 \theta >0 θ>0,有
lim n → ∞ P ( ∣ θ ^ − θ ∣ < ε ) = 1. \lim\limits_{n\to\infty}P\left(|\hat\theta-\theta| < \varepsilon\right)=1. n→∞limP(∣θ^−θ∣<ε)=1.
推导
首先来看一下在分母为n的情况下样本方差是不是总体方差的无偏估计量:
E ( S 2 ) = E [ 1 n ∑ i = 1 n ( X i − X ˉ ) 2 ] = E [ 1 n ∑ i = 1 n ( ( X i − μ ) − ( X ˉ − μ ) ) 2 ] = E [ 1 n ∑ i = 1 n ( ( X i − μ ) 2 − 2 ( X i − μ ) ( X ˉ − μ ) + ( X ˉ − μ ) 2 ) ] = E [ 1 n ∑ i = 1 n ( X i − μ ) 2 − 2 n ( X ˉ − μ ) ∑ i = 1 n ( X i − μ ) + 1 n ( X ˉ − μ ) 2 ∑ i = 1 n 1 ] = E [ 1 n ∑ i = 1 n ( X i − μ ) 2 − 2 n ( X ˉ − μ ) ∑ i = 1 n ( X i − μ ) + ( X ˉ − μ ) 2 ] \begin{aligned} E(S^2) &= E \left [ \frac{1}{n} \sum_{i=1}^{n} (X_i - \bar X)^2 \right ] \\ &= E \left [ \frac{1}{n} \sum_{i=1}^{n} \Bigg( (X_i - \mu)-(\bar X - \mu) \Bigg)^2 \right ] \\ &= E \left [ \frac{1}{n} \sum_{i=1}^{n} \Bigg( (X_i - \mu)^2-2(X_i - \mu)(\bar X - \mu)+(\bar X - \mu)^2 \Bigg) \right ] \\ &= E \left [ \frac{1}{n} \sum_{i=1}^{n} (X_i - \mu)^2- \frac{2}{n} (\bar X - \mu) \sum_{i=1}^{n}(X_i - \mu)+ \frac{1}{n} (\bar X - \mu)^2 \sum_{i=1}^{n} 1 \right ] \\ &= E \left [ \frac{1}{n} \sum_{i=1}^{n} (X_i - \mu)^2- \frac{2}{n} (\bar X - \mu) \sum_{i=1}^{n}(X_i - \mu)+ (\bar X - \mu)^2 \right ] \end{aligned} E(S2)=E[n1i=1∑n(Xi−Xˉ)2]=E n1i=1∑n((Xi−μ)−(Xˉ−μ))2 =E[n1i=1∑n((Xi−μ)2−2(Xi−μ)(Xˉ−μ)+(Xˉ−μ)2)]=E[n1i=1∑n(Xi−μ)2−n2(Xˉ−μ)i=1∑n(Xi−μ)+n1(Xˉ−μ)2i=1∑n1]=E[n1i=1∑n(Xi−μ)2−n2(Xˉ−μ)i=1∑n(Xi−μ)+(Xˉ−μ)2]
其中
X ˉ − μ = 1 n ∑ i = 1 n X i − 1 n ∑ i = 1 n μ = 1 n ∑ i = 1 n ( X i − μ ) \bar X - \mu=\frac{1}{n}\sum_{i=1}^{n} X_i-\frac{1}{n}\sum_{i=1}^{n} \mu=\frac{1}{n}\sum_{i=1}^{n} (X_i-\mu) Xˉ−μ=n1i=1∑nXi−n1i=1∑nμ=n1i=1∑n(Xi−μ)
接着计算有:
E ( S 2 ) = E [ 1 n ∑ i = 1 n ( X i − μ ) 2 − 2 n ( X ˉ − μ ) ∑ i = 1 n ( X i − μ ) + ( X ˉ − μ ) 2 ] = E [ 1 n ∑ i = 1 n ( X i − μ ) 2 − 2 n ( X ˉ − μ ) ⋅ n ⋅ ( X ˉ − μ ) + ( X ˉ − μ ) 2 ] = E [ 1 n ∑ i = 1 n ( X i − μ ) 2 − ( X ˉ − μ ) 2 ] = E [ 1 n ∑ i = 1 n ( X i − μ ) 2 ] − E [ ( X ˉ − μ ) 2 ] = σ 2 − E [ ( X ˉ − μ ) 2 ] \begin{aligned} E(S^2) &= E \left [ \frac{1}{n} \sum_{i=1}^{n} (X_i - \mu)^2- \frac{2}{n} (\bar X - \mu) \sum_{i=1}^{n}(X_i - \mu)+ (\bar X - \mu)^2 \right ] \\ &= E \left [ \frac{1}{n} \sum_{i=1}^{n} (X_i - \mu)^2- \frac{2}{n} (\bar X - \mu) \cdot n \cdot (\bar X - \mu)+ (\bar X - \mu)^2 \right ] \\ &= E \left [ \frac{1}{n} \sum_{i=1}^{n} (X_i - \mu)^2- (\bar X - \mu)^2 \right ] \\ &= E \left [ \frac{1}{n} \sum_{i=1}^{n} (X_i - \mu)^2 \right ]- E \bigg [(\bar X - \mu)^2 \bigg ] \\ &= \sigma^2-E \bigg [(\bar X - \mu)^2 \bigg ] \end{aligned} E(S2)=E[n1i=1∑n(Xi−μ)2−n2(Xˉ−μ)i=1∑n(Xi−μ)+(Xˉ−μ)2]=E[n1i=1∑n(Xi−μ)2−n2(Xˉ−μ)⋅n⋅(Xˉ−μ)+(Xˉ−μ)2]=E[n1i=1∑n(Xi−μ)2−(Xˉ−μ)2]=E[n1i=1∑n(Xi−μ)2]−E[(Xˉ−μ)2]=σ2−E[(Xˉ−μ)2]
可以看到同样在除以 n n n的情况下只有当 X ˉ = μ \bar X = \mu Xˉ=μ时才有 E ( S 2 ) = σ 2 E(S^2)= \sigma^2 E(S2)=σ2,在其他情况下 E ( S 2 ) E(S^2) E(S2)都是小于 σ 2 \sigma^2 σ2的。这一个结果也很好理解,只要样本均值 X ˉ \bar X Xˉ越偏离总体均值 μ \mu μ,样本也就越偏离总体均值。
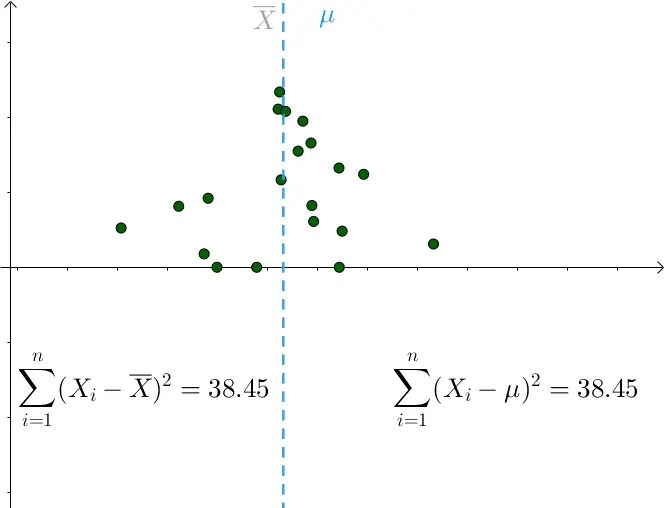
接下来就是要计算出差异 E [ ( X ˉ − μ ) 2 ] E \bigg [(\bar X - \mu)^2 \bigg ] E[(Xˉ−μ)2]是多少
由
E ( X ˉ ) = E ( 1 n ∑ i = 1 n X i ) = 1 n ∑ i = 1 n E ( X i ) = 1 n ∑ i = 1 n μ = μ E(\bar{X}) = E\bigg(\frac{1}{n} \sum_{i=1}^{n} X_i\bigg) = \frac{1}{n}\sum_{i=1}^nE(X_i) = \frac{1}{n}\sum_{i=1}^n \mu = \mu E(Xˉ)=E(n1i=1∑nXi)=n1i=1∑nE(Xi)=n1i=1∑nμ=μ
D ( a X i ) = a 2 D ( X i ) D(aX_i) = a^2 D(X_i) D(aXi)=a2D(Xi)
代入有:
E [ ( X ˉ − μ ) 2 ] = E [ ( X ˉ − E ( X ˉ ) ) 2 ] = D ( X ˉ ) = D ( 1 n ∑ i = 1 n X i ) = 1 n 2 ∑ i = 1 n D ( X i ) = 1 n 2 ⋅ n σ 2 = σ 2 n \begin{aligned} E \bigg [(\bar X - \mu)^2 \bigg ] &= E \bigg [(\bar X - E(\bar{X}))^2 \bigg ] \\ &=D(\bar{X})\\ &=D\bigg(\frac{1}{n} \sum_{i=1}^{n} X_i\bigg)\\ &=\frac{1}{n^2} \sum_{i=1}^{n} D(X_i) \\ &=\frac{1}{n^2} \cdot n \sigma^2 \\ &=\frac{\sigma^2}{n} \end{aligned} E[(Xˉ−μ)2]=E[(Xˉ−E(Xˉ))2]=D(Xˉ)=D(n1i=1∑nXi)=n21i=1∑nD(Xi)=n21⋅nσ2=nσ2
所以
E ( S 2 ) = σ 2 − E [ ( X ˉ − μ ) 2 ] = n − 1 n σ 2 E(S^2) = \sigma^2-E \bigg [(\bar X - \mu)^2 \bigg ] =\frac{n-1}{n}\sigma^2 E(S2)=σ2−E[(Xˉ−μ)2]=nn−1σ2
进行一下调整,即有
n n − 1 E ( S 2 ) = n n − 1 E [ 1 n ∑ i = 1 n ( X i − X ˉ ) 2 ] = E [ 1 n − 1 ∑ i = 1 n ( X i − X ˉ ) 2 ] = σ 2 \frac{n}{n-1}E(S^2)=\frac{n}{n-1} E \left [ \frac{1}{n} \sum_{i=1}^{n} (X_i - \bar X)^2 \right ]=E \left [ \frac{1}{n-1} \sum_{i=1}^{n} (X_i - \bar X)^2 \right ]=\sigma^2 n−1nE(S2)=n−1nE[n1i=1∑n(Xi−Xˉ)2]=E[n−11i=1∑n(Xi−Xˉ)2]=σ2
这样得到的就是无偏的估计
https://www.zhihu.com/question/20099757
https://www.zhihu.com/question/22983179
相关文章:

为什么样本方差(sample variance)的分母是 n-1?
样本均值与样本方差的定义 首先来看一下均值,方差,样本均值与样本方差的定义 总体均值的定义: μ 1 n ∑ i 1 n X i \mu\frac{1}{n}\sum_{i1}^{n} X_i μn1i1∑nXi 也就是将总体中所有的样本值加总除以个数,也可以叫做总…...

编解码器架构
一、定义 0、机器翻译是序列转换模型的一个核心问题, 其输入和输出都是长度可变的序列。 为了处理这种类型的输入和输出, 我们设计一个包含两个主要组件的架构: 第一个组件是一个编码器(encoder): 它接受一…...

追问试面试系列:JVM运行时数据区
hi 欢迎来到追问试面试系列之JVM运行时数据区,在面试中出现频率非常高,并且其中还存在一些误导性的面试,一定要注意。 什么误导性呢?面试中,有的面试官本来是想问JVM运行时数据区,不过提问时难免有些让你觉得很不爽。比如:你说说java内存模型,还比如说说JVM内存模型,…...

React Native在移动端落地实践
在移动互联网产品迅猛发展的今天,技术的不断创新使得企业越来越注重降低成本、提升效率。为了在有限的开发资源下迅速推出高质量、用户体验好的产品,以实现公司发展,业界催生了许多移动端跨平台解决方案。这些方案不仅简化了开发流程…...

《操作系统》(学习笔记)(王道)
一、计算机系统概述 1.1 操作系统的基本概念 1.1.1 操作系统的概念 1.1.2 操作系统的特征 1.1.3 操作系统的目标和功能 1.2 操作系统的发展与分类 1.2.1 手工操作阶段(此阶段无操作系统) 1.2.2 批处理阶段(操作系统开始出现࿰…...

LabVIEW学习-LabVIEW处理带分隔符的字符串从而获取数据
带分隔符的字符串很好处理,只需要使用"分隔符字符串至一维字符串数组"函数或者"一维字符串数组至分隔符字符串"函数就可以很轻松地处理带分隔符地字符串。 这两个函数所在的位置为: 函数选板->字符串->附加字符串函数->分…...

freesql简单使用操作mysql数据库
参考:freesql中文官网指南 | FreeSql 官方文档 这两天准备做一个测试程序,往一个系统的数据表插入一批模拟设备数据,然后还要模拟设备终端发送数据包,看看系统的承压能力。 因为系统使用的第三方框架中用到了freesql,…...

使用Java和Spring Retry实现重试机制
使用Java和Spring Retry实现重试机制 大家好,我是微赚淘客系统3.0的小编,是个冬天不穿秋裤,天冷也要风度的程序猿!今天,我们将探讨如何在Java中使用Spring Retry来实现重试机制。重试机制在处理临时性故障和提高系统稳…...
:自定义配置与插件管理)
Linux Vim教程(十):自定义配置与插件管理
目录 1. 概述 2. Vim 配置文件 2.1 .vimrc 文件 2.2 .gvimrc 文件 3. 自定义配置 3.1 自定义快捷键 3.2 自动命令 3.3 函数定义 4. 插件管理 4.1 插件管理工具 4.1.1 安装 vim-plug 4.1.2 配置 vim-plug 4.1.3 安装插件 4.2 常用插件 4.2.1 NERDTree 4.2.2 Fzf…...

代理协议解析:如何根据需求选择HTTP、HTTPS或SOCKS5?
代理IP协议是一种网络代理技术,可以实现隐藏客户端IP地址、加速网站访问、过滤网络内容、访问内网资源等功能。常用的IP代理协议主要有Socks5代理、HTTP代理、HTTPS代理这三种。代理IP协议主要用于分组交换计算机通信网络的互联系统中使用,只负责数据的路…...
Verilog语言和C语言的本质区别是什么?
在开始前刚好我有一些资料,是我根据网友给的问题精心整理了一份「C语言的资料从专业入门到高级教程」, 点个关注在评论区回复“888”之后私信回复“888”,全部无偿共享给大家!!! 用老石的一句话其实很好说…...

Delphi5实现鱼C屏幕保护程序
效果图 鱼C屏幕保护程序 添加背景图片 在additional添加image组件,修改picture属性上传图片。 这个图片可以截屏桌面,方便后面满屏不留白操作。实现无边框 即上面的“- □ ”不显示 将Form1的borderstyle属性改为bsnone实现最大化,满屏 将…...

【计算机毕业设计】844学籍管理系统
🙊作者简介:拥有多年开发工作经验,分享技术代码帮助学生学习,独立完成自己的项目或者毕业设计。 代码可以私聊博主获取。🌹赠送计算机毕业设计600个选题excel文件,帮助大学选题。赠送开题报告模板ÿ…...

Java之开发 系统设计 分布式 高性能 高可用
1、restful api 基于rest构建的api 规范: post delete put get 增删改查路径 接口命名 过滤信息状态码 2、软件开发流程 3、命名规范 类名:大驼峰方法名:小驼峰成员变量、局部变量:小驼峰测试方法名:蛇形命名 下划…...

java连接redis和基础操作命令
引入依赖 <!--引入java连接redis的驱动--><dependency><groupId>redis.clients</groupId><artifactId>jedis</artifactId><version>4.3.1</version></dependency> 单机模式连接redis main(){ //连接redis的信息 默认连接…...

土耳其云手机提升TikTok电商效率
在数字化飞速发展的今天,TikTok不仅是一个社交平台,更是一个巨大的电商市场。随着TikTok电商功能在全球范围内的扩展,土耳其的商家和内容创作者正面临着前所未有的机遇。本文将详细介绍土耳其云手机怎样帮助商家抓住机遇,实现业务…...

《Utilizing Ensemble Learning for Detecting Multi-Modal Fake News》
系列论文研读目录 文章目录 系列论文研读目录论文题目含义ABSTRACTINDEX TERMSI. INTRODUCTIONII. RELATED WORKA. FAKE NEWS CLASSIFICATION APPROACHES FOR SINGLE-MODALITY 单模态虚假新闻分类方法1) SINGLE-MODALITY BASED CLASSIFICATION APPROACHES USING TEXTUAL FEATUR…...

Oracle集群RAC磁盘管理命令asmcmd的使用
文章目录 ASM磁盘共享简介ASM磁盘共享的优势ASM磁盘组成ASM磁盘共享的应用场景Asmcmd简介Asmcmd的功能Asmcmd的命令Asmcmd的使用注意事项Asmcmd运行模式交互模式运行非交互模式运行ASMCMD命令分类实例管理命令:文件管理命令:磁盘组管理命令:模板管理命令:文件访问管理命令:…...

vscode插件开发笔记——大模型应用之AI编程助手
系列文章目录 文章目录 系列文章目录前言一、代码补全 前言 最近在开发vscode插件相关的项目,网上很少有关于大模型作为AI 编程助手这方面的教程。因此,借此机会把最近写的几个demo分享记录一下。 一、代码补全 思路: 读取vscode插件上鼠…...

@JSONField(format = “yyyyMMddHH“)的作用和使用
JySellerItqrdDataDO对象中的字段为: private Date crdat; 2.数据库中的相应字段为: crdat datetime DEFAULT NULL COMMENT 创建时间,2. 打印出的结果为: “crdat”:“2024072718” 年月日时分秒 3. 可以调整format的格式 4. 这样就把Date类…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...
