【算法/训练】:动态规划(线性DP)
一、路径类
1. 字母收集

思路:
1、预处理
对输入的字符矩阵我们按照要求将其转换为数字分数,由于只能往下和往右走,因此走到(i,j)的位置要就是从(i - 1, j)往下走,或者是从(i,j - 1)的位置往右走,由于我们要使得路程遍历积分最多,则应该从积分多的位置过来,
2、状态表示 dp[i][j] 表示:从[0, 0]出发,到底[i, j]位置,一共有多少分
3、状态转移方程
故(i,j)位置的积分应该为dp[ i ][ j ] = max(dp[ i - 1 ][ j ], dp[ i ][ j - 1 ]) + dp[ i ][ j ];
4、初始化
但是上面仅对于(i >= 1 && j >= 1)成立,对于第一行和第一列我们应该特殊处理,利用前缀和的知识可以求得,走到第一列的第i个位置最多能拿的积分以及走到第一行的第j个位置最多能拿的积分,然后我们就可以按照dp[ i ][ j ] = max(dp[ i - 1 ][ j ], dp[ i ][ j - 1 ]) + dp[ i ][ j ]的方法遍历每个节点即可
#include <iostream>
using namespace std;const int N = 1005;
int dp[N][N];int main() {int n, m;cin >> n >> m;char ch;for (int i = 0; i < n; i++){for (int j = 0; j < m; j++){cin >> ch;if (ch == 'l') dp[i][j] = 4;else if (ch == 'o') dp[i][j] = 3;else if (ch == 'v') dp[i][j] = 2;else if (ch == 'e') dp[i][j] = 1;else a[i][j] = 0;}}for (int i = 1; i < n; i++) dp[i][0] = dp[i - 1][0] + dp[i][0];
for (int j = 1; j < m; j++) dp[0][j] = dp[0][j - 1] + dp[0][j]; for (int i = 1; i < n; i++){for (int j = 1; j < m; j++){dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]) + dp[i][j];}}cout << dp[n - 1][m - 1] << endl;return 0;
}
2、[NOIP2002 普及组] 过河卒

分析:

思路:
1、状态表示
dp[i][j] 表示:从[0, 0]出发,到底[i, j]位置,一共有多少种方法
2、状态转移方程dp[ i ][ j ] = dp[ i - 1 ][ j ] + dp[i][j - 1] (i > 0 && j > 0)
当走到马可以走的地方,dp[ i ][ j ] = 0;
3、初始化先创建一个 dp[ n + 2 ][ m + 2 ],然后让dp[ 0 ][ 1 ] = 1 或者 dp[ 1 ][ 0 ] = 1。注意这样初始化的时候,x需要+1,y也需要+1.和dp表位置一一对应
#include <iostream>
#include <vector>
using namespace std;//int dp[1005][1005];
int main()
{int n, m, x, y;cin >> n >> m >> x >> y;vector<vector<long long>> dp(n + 2, vector<long long>(m + 2));dp[0][1] = 1;x += 1, y += 1;和dp表位置一一对应for (int i = 1; i <= n + 1; i++){for (int j = 1; j <= m + 1; j++) { //马所在位置if (i != x && j != y && abs(i - x) + abs(j - y) == 3 || (i == x && j == y)){dp[i][j] == 0;}else dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}}cout << dp[n + 1][m + 1] << endl;return 0;
}二、子序列和连续序列类
1. mari和shiny

🌈线性 dp
在维护 i 位置之前,⼀共有多少个 "s" "sh" ,然后更新 "shy" 的个数。
(1)状态表示
s[i]:字符串 str 中 [0, i] 区间内有多少个 "s"。
h[i]:字符串 str 中 [0, i] 区间内有多少个 "sh"。
y[i]:字符串 str 中 [0, i] 区间内有多少个 "shy。
(2)状态转移方程
(3)空间优化
用三个变量来表示即可
s:(字符串 str 中 [0, n-1] 区间内有多少个 "s")
h:(字符串 str 中 [0, n-1] 区间内有多少个 "sh")
y:(字符串 str 中 [0, n-1] 区间内有多少个 "shy")
最后的遍历结束后,y即我们需要的结果
#include <iostream>
#include <string>
using namespace std;
typedef long long ll;
int main()
{int n;string str;cin >> n >> str;ll s = 0, h = 0, y = 0;for (int i = 0; i < n; i++) {if (str[i] == 's') s++;else if (str[i] == 'h') h += s;else if (str[i] == 'y') y += h;}cout << y << endl;return 0;
}🌈二维 dp
这道题目如果不是子序列,而是要求连续序列的,那就可以考虑用 KMP。
(1)dp[i][j] 含义
- string t="shy"
dp[i][j]:以 i-1 为结尾的 str 子序列中出现以 j-1 为结尾的 t 的个数为 dp[i][j]。
(2)递推关系
- str[i - 1] 与 t[j - 1]相等
- str[i - 1] 与 t[j - 1] 不相等
当 str[i - 1] 与 t[j - 1]相等时,dp[i][j] 可以有两部分组成:
- 一部分是用 str[i - 1] 来匹配,那么个数为 dp[i - 1][j - 1]。即不需要考虑当前 str 子串和 t 子串的最后一位字母,所以只需要 dp[i-1][j-1]。
- 一部分是不用 str[i - 1] 来匹配,个数为 dp[i - 1][j]。
为什么还要考虑不用 str[i - 1] 来匹配,都相同了指定要匹配?
🧩例如: str:shyy 和 t:shy ,str[3] 和 t[2] 是相同的,但是字符串 str 也可以不用 str[3] 来匹配,即用 str[0]str[1]str[2] 组成的 "shy"。当然也可以用 str[3] 来匹配,即:str[0]str[1]str[3] 组成的 "shy"。所以,当 str[i - 1] 与 t[j - 1] 相等时,dp[ i ][ j ] = dp[ i - 1 ][ j - 1 ] + dp[ i - 1 ][ j ];
当 str[i - 1] 与 t[j - 1] 不相等时,dp[i][j] 只有一部分组成,不用 str[i - 1] 来匹配(就是模拟在 str 中删除这个元素),即:dp[i - 1][j],所以递推公式为:dp[ i ][ j ] = dp[ i - 1 ][ j ];
为什么只考虑 “不用 str[i - 1] 来匹配” 这种情况, 不考虑 “不用 t[j - 1] 来匹配” 的情况呢?
🧩这里要明确,我们求的是 str 中有多少个 t,而不是求 t 中有多少个 str,所以只考虑 str 中删除元素的情况,即不用 str[i - 1] 来匹配 的情况。
(3)状态转移方程
dp[i][j]显然要从dp[i-1][?]递推而来。立即思考dp[i-1][j], dp[i-1][j-1]分别与dp[i][j]的关系。因为少一个字符,自然而然从当前字符着手。考察si的第i个字符(表为s[i])和tj的第j个字符(表为t[j])的关系。
若s[i] ≠ t[j]:那么s_i中的所有t_j子序列,必不包含s[i],即s_i-1和s_i中tj的数量是一样的,得到该情形的转移方程: dp[ i ][ j ] = dp[ i -1 ][ j ]
若s[i] = t[j]:假设s_i中的所有t_j子序列中,包含s[i]的有a个,不包含的有b个。s_i中包含s[i]的子序列个数相当于s_i-1中t_j-1的个数,不包含s[i]的子序列个数与上一种情况一样,于是得到该情形的转移方程:
a = dp[ i -1 ][ j -1 ] b = dp[ i-1 ][ j ] dp[ i ][ j ] = a + b = dp[i-1][j-1] + dp[i-1][j]
(4)遍历顺序
从上到下,从左到右。
#include <iostream>
#include <vector>using namespace std;int main()
{int n;cin >> n;string str;cin >> str;string t="shy";int m=t.size();vector<vector<long long>> dp(n+1, vector<long long>(m+1));for(int i=0; i<=n; i++) dp[i][0]=1;for(int i=1; i<=n; i++){for(int j=1; j<=m; j++){if(str[i-1]==t[j-1])dp[i][j]=dp[i-1][j-1]+dp[i-1][j];elsedp[i][j]=dp[i-1][j];}}cout << dp[n][m] << endl;return 0;
}2. 不同的子序列

该题于上题不一样的是,上面给定了t的具体字符串,而这里没有给定,但是我们也需要用二维dp的方法来写。
(1)dp[i][j] 含义
s[ i ]的子序列中在t[ j ]出现的次数
s[ i ]表示s从下标 i 到末尾的子字符串。
t[ j ]表示t从下标 j 到末尾的子字符串。
(2)递推关系
- 分别令两个维度为0,推测边界。
- dp[0][j]表示s_0中t_j的个数。s_0是空字符串,只有当j=0时,才有dp[0][j] = 1,表示s子空串中有一个t子空串,否则dp[0][j] = 0,因为一个空串不可能包含一个非空串。
dp[i][0]表示s_i中t0的个数。t_0是空字符串,显然任何串(包括空串)都含有一个空子串。因此dp[i][0] = 1。
注意到,dp[i][0] = 1实际上已经包含了dp[0][j] = 1的情形。
(3)初始化
- dp[i][0] 表示:以 i-1 为结尾的 str 可以随便删除元素,出现空字符串的个数。所以,dp[i][0] 一定都是 1,因为也就是把以 i-1 为结尾的 str,删除所有元素,出现空字符串的个数就是 1。
- dp[0][j] 表示:空字符串 str 可以随便删除元素,出现以 j-1 为结尾的字符串 t 的个数。所以,dp[0][j] 一定都是 0,因为 str 如论如何也变成不了 t。
- dp[0][0] 表示:空字符串 str 可以删除 0 个元素,变成空字符串 t。所以,dp[0][0] = 1。
(4)遍历顺序
从上到下,从左到右。
int numDistinct(string s, string t) {int n = s.size(), m = t.size();if (n < m) return 0;vector<vector<unsigned int>> dp(n + 1, vector<unsigned int>(m + 1)); //注意是unsigned intfor (int i = 0; i <= n; i++) dp[i][0] = 1;for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {dp[i][j] = dp[i - 1][j] +(s[i - 1] == t[j - 1] ? dp[i - 1][j - 1] : 0);}}return dp[n][m];
}相关文章:

【算法/训练】:动态规划(线性DP)
一、路径类 1. 字母收集 思路: 1、预处理 对输入的字符矩阵我们按照要求将其转换为数字分数,由于只能往下和往右走,因此走到(i,j)的位置要就是从(i - 1, j)往下走&#…...

计算巨头 Azure、AWS 和 GCP 的比较
云计算领域由三大主要参与者主导:Microsoft Azure、Amazon Web Services (AWS) 和 Google Cloud Platform (GCP)。每个平台都为希望利用云提供基础设施、平台服务等的企业提供强大的功能。在本文中,我们将深入探讨这些平台之间的差异,重点关注…...

Thinkphp5跨域问题常见的处理方法
在ThinkPHP5中,处理跨域问题通常涉及配置中间件或直接在控制器中设置响应头。以下是几种常见的解决跨域问题的方法: 1. 使用中间件处理跨域 你可以创建一个中间件来专门处理跨域请求。这个中间件会检查请求的来源,并设置相应的响应头来允许…...

Matlab编程资源库(9)数据插值与曲线拟合
一、一维数据插值 在MATLAB中,实现这些插值的函数是interp1,其调用格式为: Y1interp1(X,Y,X1,method) 函数根据X,Y的值,计算函数在X1处的值。X,Y是两个等长的已知向量,分别描述采样点和样本值,X1是一个向量…...

matplotlib的科研绘图辅助
matplotlib的科研绘图辅助 趁着暑假,与和鲸科技合作了一个python绘图的教程,作为暑期夏令营的一小部分,主要内容是介绍如何使用matplotlib、pandas、seaborn和plotnine进行医学科研绘图,感兴趣的可以通过如下地址进行访问&#x…...

C++内存管理(候捷)第五讲 笔记
GNU C对allocators的描述 new_allocator 和malloc_allocator,它们都没有特别的动作,无非底部调用operator new和malloc。它们没有用内存池 区别:::operator new是可重载的 智能型的allocator,使用内存池,分一大块然后…...

谷粒商城实战笔记-63-商品服务-API-品牌管理-OSS获取服务端签名
文章目录 一,创建第三方服务模块thrid-party1,创建一个名为gulimall-third-party的模块2,nacos上创建third-party命名空间,用来管理这个服务的所有配置3,配置pom文件4,配置文件5,单元测试6&…...

详细介绍BIO、NIO、IO多路复用(select、poll、epoll)
BIO、NIO、IO多路复用 BIO(Blocking IO)NIO(Non-blocking IO) 同步非阻塞IOIO多路复用selectpollepoll Redis的IO多路复用 BIO(Blocking IO) 最基础的IO模型,当进行IO操作时,线程会被阻塞,直到操作完成。 比如read和write,通常IO…...

昇思25天学习打卡营第11天|xiaoyushao
今天分享ResNet50迁移学习。 在实际应用场景中,由于训练数据集不足,所以很少有人会从头开始训练整个网络。普遍的做法是,在一个非常大的基础数据集上训练得到一个预训练模型,然后使用该模型来初始化网络的权重参数或作为固定特征提…...
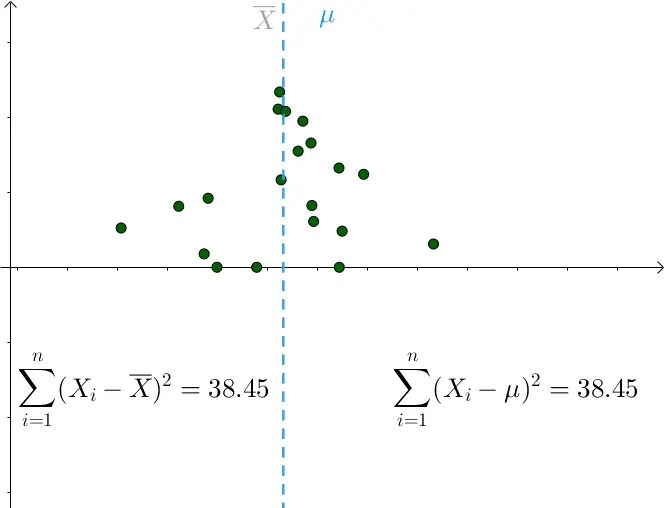
为什么样本方差(sample variance)的分母是 n-1?
样本均值与样本方差的定义 首先来看一下均值,方差,样本均值与样本方差的定义 总体均值的定义: μ 1 n ∑ i 1 n X i \mu\frac{1}{n}\sum_{i1}^{n} X_i μn1i1∑nXi 也就是将总体中所有的样本值加总除以个数,也可以叫做总…...

编解码器架构
一、定义 0、机器翻译是序列转换模型的一个核心问题, 其输入和输出都是长度可变的序列。 为了处理这种类型的输入和输出, 我们设计一个包含两个主要组件的架构: 第一个组件是一个编码器(encoder): 它接受一…...

追问试面试系列:JVM运行时数据区
hi 欢迎来到追问试面试系列之JVM运行时数据区,在面试中出现频率非常高,并且其中还存在一些误导性的面试,一定要注意。 什么误导性呢?面试中,有的面试官本来是想问JVM运行时数据区,不过提问时难免有些让你觉得很不爽。比如:你说说java内存模型,还比如说说JVM内存模型,…...

React Native在移动端落地实践
在移动互联网产品迅猛发展的今天,技术的不断创新使得企业越来越注重降低成本、提升效率。为了在有限的开发资源下迅速推出高质量、用户体验好的产品,以实现公司发展,业界催生了许多移动端跨平台解决方案。这些方案不仅简化了开发流程…...

《操作系统》(学习笔记)(王道)
一、计算机系统概述 1.1 操作系统的基本概念 1.1.1 操作系统的概念 1.1.2 操作系统的特征 1.1.3 操作系统的目标和功能 1.2 操作系统的发展与分类 1.2.1 手工操作阶段(此阶段无操作系统) 1.2.2 批处理阶段(操作系统开始出现࿰…...

LabVIEW学习-LabVIEW处理带分隔符的字符串从而获取数据
带分隔符的字符串很好处理,只需要使用"分隔符字符串至一维字符串数组"函数或者"一维字符串数组至分隔符字符串"函数就可以很轻松地处理带分隔符地字符串。 这两个函数所在的位置为: 函数选板->字符串->附加字符串函数->分…...

freesql简单使用操作mysql数据库
参考:freesql中文官网指南 | FreeSql 官方文档 这两天准备做一个测试程序,往一个系统的数据表插入一批模拟设备数据,然后还要模拟设备终端发送数据包,看看系统的承压能力。 因为系统使用的第三方框架中用到了freesql,…...

使用Java和Spring Retry实现重试机制
使用Java和Spring Retry实现重试机制 大家好,我是微赚淘客系统3.0的小编,是个冬天不穿秋裤,天冷也要风度的程序猿!今天,我们将探讨如何在Java中使用Spring Retry来实现重试机制。重试机制在处理临时性故障和提高系统稳…...
:自定义配置与插件管理)
Linux Vim教程(十):自定义配置与插件管理
目录 1. 概述 2. Vim 配置文件 2.1 .vimrc 文件 2.2 .gvimrc 文件 3. 自定义配置 3.1 自定义快捷键 3.2 自动命令 3.3 函数定义 4. 插件管理 4.1 插件管理工具 4.1.1 安装 vim-plug 4.1.2 配置 vim-plug 4.1.3 安装插件 4.2 常用插件 4.2.1 NERDTree 4.2.2 Fzf…...

代理协议解析:如何根据需求选择HTTP、HTTPS或SOCKS5?
代理IP协议是一种网络代理技术,可以实现隐藏客户端IP地址、加速网站访问、过滤网络内容、访问内网资源等功能。常用的IP代理协议主要有Socks5代理、HTTP代理、HTTPS代理这三种。代理IP协议主要用于分组交换计算机通信网络的互联系统中使用,只负责数据的路…...
Verilog语言和C语言的本质区别是什么?
在开始前刚好我有一些资料,是我根据网友给的问题精心整理了一份「C语言的资料从专业入门到高级教程」, 点个关注在评论区回复“888”之后私信回复“888”,全部无偿共享给大家!!! 用老石的一句话其实很好说…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...


