关于顺序表数组下标的一些关系梳理


相关文章:

关于顺序表数组下标的一些关系梳理
...

VS C++ Project(项目)的工作目录设置
如果只是简单创建一个VS CProject或者MFC Project,可能很多时候,只关心将Project放在硬盘的那个位置,与Project目录相关的的其他问题,并不引人注意,我们也不是十分在意。有时我们不得不进行工作目录方面的设置…...

STM32自定义协议串口接收解析指令程序
1、在使用串口接收自定义协议指令时,需要串口解析收到的是什么指令,举例通信报文为 上位机->单片机 名称 长度 备注 帧头 1Byte 0x5A 0x5A 帧长度 1Byte 数据包的长度0x00-0xFF 数据包 命令字 1Byte 功能标识 数据 可以为空 校验 …...

STM32——GPIO(点亮LEDLED闪烁)
一、什么是GPIO? GPIO(通用输入输出接口): 1.GPIO 功能概述 GPIO 是通用输入/输出(General Purpose I/O)的简称,既能当输入口使用,又能当输出口使用。端口,就是元器件…...

VulnHub靶机入门篇--kioptrix.level 3
1.环境准备 靶机:Kioptrix Level 3(Nat模式) 下载地址:https://download.vulnhub.com/kioptrix/KVM3.rar 攻击机:kali(192.168.26.128)(Nat模式) 2.渗透测试 信息收…...

aiGPT系统源码★重大升级★AI写作/AI绘画/AI音乐/AI视频
亲爱老铁们好,又一段时间未更新内容了,我依然是爱你们的神点妹,今天点妹给大家带来一波新的福利:咱们用的aiGPT经过攻城师们近半年来夜以继日的技术升级,今天终于迎来了新版上线首秀。此次升级内容包含:首先…...

Vue Router高级用法:动态路由与导航守卫
Vue Router是Vue.js官方的路由管理器,它和Vue.js的核心深度集成,让构建单页应用变得轻而易举。 动态路由 动态路由允许你在路由路径中使用变量,这些变量可以从实际的URL中获取,并传递给对应的路由组件。 定义动态路由 在route…...

江科大/江协科技 STM32学习笔记P9-11
文章目录 OLED1、OLED硬件main.c EXTI外部中断1、中断系统2、中断执行流程图3、STM32中断4、中断地址的作用5、EXTI6、EXTI基本结构7、AFIO复用IO口8、EXTI框图或门和与门 9、旋转编码器介绍10、硬件电路 OLED 1、OLED硬件 SCL和SDA是I2C的通信引脚,需要接在单片机…...

【培训通知】成为Power BI数据分析可视化实战第一人,加入3天直播即可
Power BI数据分析可视化实战课程培训是一门旨在提升学员在数据分析与可视化领域能力的专业课程。以下是对该培训课程的详细介绍: 一、课程概述 Power BI 是一种业务分析服务,能够提供深入的见解,帮助用户实现快速、明智的决策。该课程通过实…...

24暑假算法刷题 | Day22 | LeetCode 77. 组合,216. 组合总和 III,17. 电话号码的字母组合
目录 77. 组合题目描述题解 216. 组合总和 III题目描述题解 17. 电话号码的字母组合题目描述题解 77. 组合 点此跳转题目链接 题目描述 给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。 你可以按 任何顺序 返回答案。 示例 1: 输…...

一篇文章告诉你对讲机为什么不能被手机取代的7个原因
在智能时代,手机几乎无处不在,涵盖了从基本通信到多媒体娱乐的一切功能。然而,即使在这种情况下,对讲机仍然没有被完全取代。这不仅仅是出于怀旧或专业需求,还有许多实质性的原因使得对讲机在特定领域和情况下仍然保持…...

LION论文阅读
一、论文主要出发点 3D目标检测的性能受限于3D卷积的局部感受野。 Transformer在3D检测领域效果很好,但由于算力限制,已有的工作在pillar内,或将voxel分组在组内进行特征交互,阻碍了他们捕捉更远程的依赖关系。 线性RNN算子的计…...

在Android上实现汉字笔顺动画效果——HanZiWriter
序,万般皆是命,半点不由人。 Hanzi Writer 是 javascript 免费开源库,根据汉字书写时按照笔画顺序的特征,可以播放正确笔画顺序的描边动画和练习测试。支持简体字和繁体字。可以让全球用户能够通过手绘模仿的方式来学习和练习书写…...

黑马头条vue2.0项目实战(一)——项目初始化
1. 图标素材(iconfont简介) 制作字体图标的工具有很多,推荐使用:iconfont-阿里巴巴矢量图标库。 注册账户 创建项目 可以根据项目自定义 class 前缀 上传图标到项目 生成链接,复制 css 代码,在项目中使用…...

Unity Shader动画:用代码绘制动态视觉效果
在Unity中,Shader是运行在GPU上的小程序,用于控制顶点和像素的渲染过程。通过编写自定义Shader,开发者可以创造出各种令人惊叹的动画效果,从简单的颜色变化到复杂的流体模拟。本文将探讨如何使用Unity Shader来实现动画效果。 Sh…...
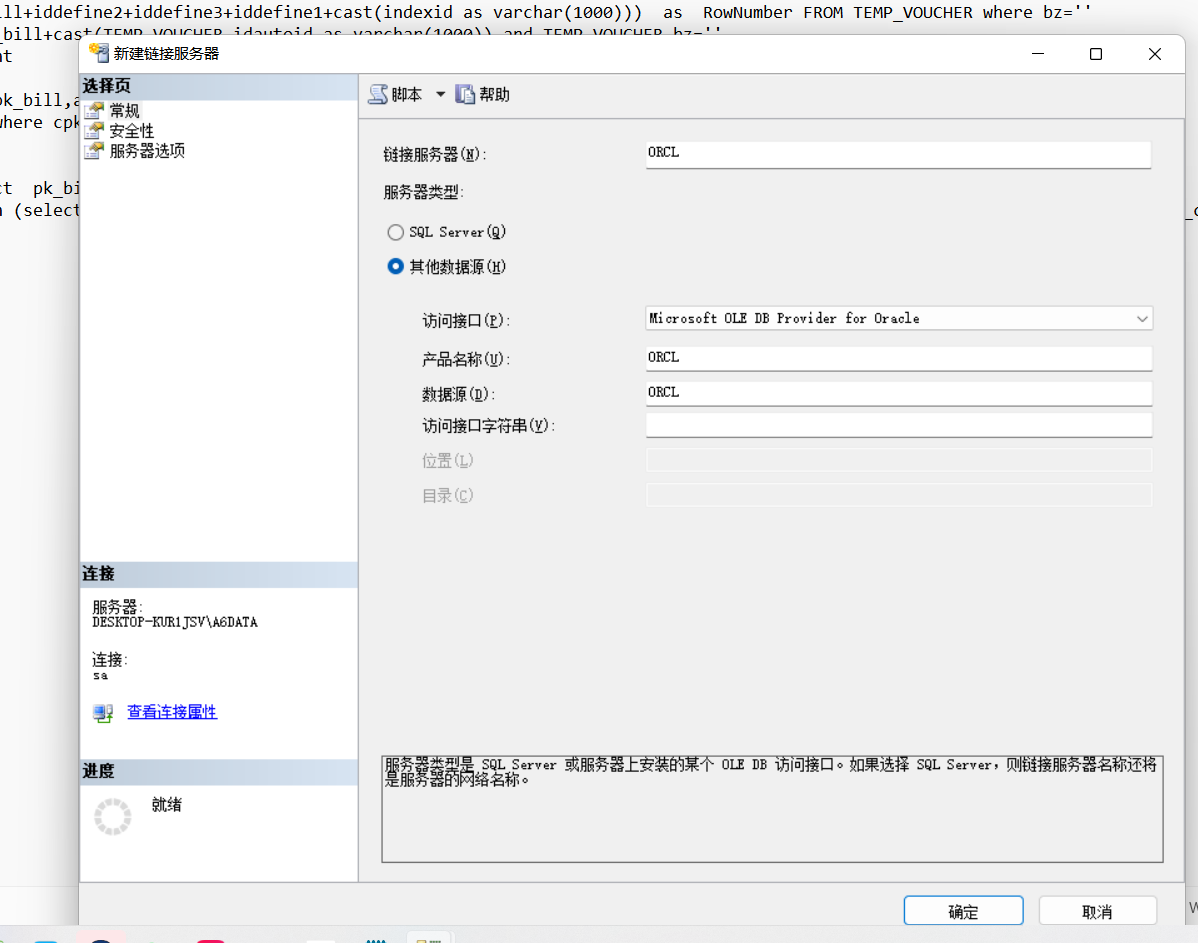
智税集成2.0生成凭证
:::info 💡 整体业务流程 从A9服务器中取数,生成列表数据,写入到对方oracle数据库中。 ::: 项目关键点 1.连接数据库 左连接连接本地SQLserver数据库、右连接要链接A9开票服务器的数据库然后设想用SQLserver 自带的外部连接来连接oracle数据…...

B4005 [GESP202406 四级] 黑白方块 【暴力枚举】【前缀和】
#include<bits/stdc.h> using namespace std; int n,m,ans,tmp; char mp[20][20]; int cheak(int a,int b,int c,int d){//a<c b<dint cnt0;//枚举矩阵中的每个点 for(int ia;i<c;i)for(int jb;j<d;j)if(mp[i][j]1) cnt;//统计黑格的个数 return 2*cnt(c-a1…...

深度学习趋同性的量化探索:以多模态学习与联合嵌入为例
深度学习趋同性的量化探索:以多模态学习与联合嵌入为例 参考文献 据说是2024年最好的人工智能论文,是否有划时代的意义? [2405.07987] The Platonic Representation Hypothesis (arxiv.org) arxiv.org/abs/2405.07987 趋同性的量化表达 …...

决策树与随机森林:比较与应用场景分析
决策树与随机森林:比较与应用场景分析 引言 决策树和随机森林是机器学习中广泛使用的两种算法,因其简单性和强大的功能而被广泛采用。决策树是一种树形结构的决策模型,易于理解和解释。随机森林则是通过集成多棵决策树来提高预测性能的模型…...

C#用Aspose.Cells导出Excel,.NET导出Excel
ASP.NET MVC 控制器里面Action处理,下载文件,输出文件流 public async Task<ActionResult> ExportNewsAuthorFee(string deptId, DateTime? startDate, DateTime? endDate){if (startDate null){startDate DateTime.Parse(DateTime.Now.Year …...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...
