LeetCode 面试经典 150 题 | 位运算
目录
- 1 什么是位运算?
- 2 67. 二进制求和
- 3 136. 只出现一次的数字
- 4 137. 只出现一次的数字 II
- 5 201. 数字范围按位与
1 什么是位运算?
✒️ 源自:位运算 - 菜鸟教程
在现代计算机中,所有数据都以二进制形式存储,即 0 0 0 和 1 1 1 两种状态。计算机对二进制数据进行的运算(如:加、减、乘、除)被称为位运算,即对二进制数的每一位进行操作的运算。
为了更好地理解位运算,举个简单的例子:假设我们有如下代码进行两个整数的加法运算:
int a = 35;
int b = 47;
int c = a + b;
计算机会将这两个整数转换为二进制形式,然后进行加法运算:
35: 0010 0011
47: 0010 1111
--------------
82: 0101 0010
因此,与直接使用 + + +、 − - −、 ∗ * ∗、 / / / 运算符相比,合理运用位运算可以显著提高代码在机器上的执行效率。
✒️ 位运算概览
| 符号 | 描述 | 运算规则 |
|---|---|---|
| & | 与 | 两个位都为 1 时,结果才为 1 |
| | | 或 | 两个位都为 0 时,结果才为 0 |
| ^ | 异或 | 两个位相同为 0,相异为 1 |
| ~ | 取反 | 0 变 1,1 变 0 |
| << | 左移 | 各二进制位全部左移若干位,高位丢弃,低位补 0 |
| >> | 右移 | 各二进制位全部右移若干位,高位补 0 或符号位补齐 |
2 67. 二进制求和
假设需要计算 a a = 111 aa=111 aa=111 和 b b = 101 bb=101 bb=101 的和,那么可以将每一位的计算结果分为本位和进位:

让我们从右往左看整个计算过程:
- ① 首先是 1 + 1 1+1 1+1,本位是 0 0 0,进位是 1 1 1;
- ② 然后是 1 + 0 1+0 1+0,本位是 1 1 1,进位是 0 0 0;
- ③ 最后是 1 + 1 1+1 1+1,本位是 0 0 0,进位是 1 1 1。
通常会在 ② 中加上 ① 产生的进位,即在处理当前位的时候考虑上一位的进位。与之相反,我们不单独考虑进位,而是对进位进行统一处理,即先计算出所有的本位以及所有的进位,再对二者进行求和。
继续来看上面的计算过程,我们已经得到:
- 本位 = 0...0010 =0...0010 =0...0010
- 进位 = 0...1010 =0...1010 =0...1010
然后再计算本位和进位的和,得到新的本位和进位。重复上述操作,直到进位为 0 0 0,即没有进位时为止。
核心代码
auto ans = aa ^ bb; // 按位异或计算本位
auto carry = (aa & bb) << 1; // 按位与计算进位
其中变量 a n s \mathrm{ans} ans 用于存储所有本位,变量 c a r r y \mathrm{carry} carry 用于存储所有进位。
由于进位是指进到更高的一位,因此需要对按位与的结果进行左移一位的操作。
完整代码
string addBinary(string a, string b) {// 转换为二进制串auto aa = bitset<10001>(a);auto bb = bitset<10001>(b);// 求和while (bb != 0) {auto ans = aa ^ bb;auto carry = (aa & bb) << 1;aa = ans;bb = carry;}// 去除多余的前缀零string ans = aa.to_string();int pos = ans.find('1');if (pos > ans.size()) ans = "0";else ans = ans.substr(pos);return ans;
}
3 136. 只出现一次的数字
题目信息:除了某个元素只出现一次以外,其余每个元素均出现两次,找出那个只出现了一次的元素。
假设元素分别为 a 1 , a 2 , . . . , a n a_1,a_2,...,a_n a1,a2,...,an,根据异或操作的定义可知:
a i ⊗ a i = 0 a_i \otimes a_i = 0 ai⊗ai=0
如果是 a 7 a_7 a7 元素只出现了一次,那么有:
a 1 ⊗ a 2 ⊗ . . . ⊗ a 7 ⊗ . . . ⊗ a n = 0 ⊗ a 7 ⊗ 0 = a 7 a_1 \otimes a_2 \otimes ... \otimes a_7 \otimes ... \otimes a_n = 0 \otimes a_7 \otimes 0 = a_7 a1⊗a2⊗...⊗a7⊗...⊗an=0⊗a7⊗0=a7
因此,我们只要对所有元素进行异或,就能找出那个只出现了一次的元素。
完整代码
int singleNumber(vector<int>& nums) {int ans = 0;for (auto & num : nums)ans ^= num;return ans;
}
4 137. 只出现一次的数字 II
本题一看就是上一题的姊妹题,但是完全不能用上一题的思路做。
本题思路:对于数组中非答案的元素,每一个元素都出现了 3 3 3 次,对应着第 i i i 个二进制位的 3 3 3 个 0 0 0 或 3 3 3 个 1 1 1。无论是哪一种情况, 0 0 0 或 1 1 1 的个数都是 3 3 3 的倍数。现在计算所有元素的第 i i i 个二进制位为 1 1 1 的个数,如果不为 3 3 3 的倍数,那么多余的 1 1 1 一定是答案的第 i i i 个二进制位提供的,即答案的第 i i i 个二进制位为 1 1 1;否则为 0 0 0。
说明:“答案” 是指那个只出现了一次的元素。
完整代码
int singleNumber(vector<int>& nums) {int ans = 0;for (int i = 0; i < 32; ++i) {int cnt = 0;for (auto & num : nums) {if (num >> i & 1)++cnt;}if (cnt % 3 == 1)ans |= 1 << i;}return ans;
}
这种解法属于是通用解法了,完全可以用来解决上一题。不过思路这么繁琐,我用哈希表不香吗 😇
5 201. 数字范围按位与
假设 l e f t \mathrm{left} left 和 r i g h t \mathrm{right} right 的前 i i i 位相同,由于 l e f t < r i g h t \mathrm{left<right} left<right 且第 i + 1 i+1 i+1 位不同,因此 l e f t \mathrm{left} left 的第 i + 1 i+1 i+1 位必为 0 0 0, r i g h t \mathrm{right} right 的第 i + 1 i+1 i+1 位必为 1 1 1(从左往右数)。由于前 i i i 位相同,因此按位与的结果等于前 i i i 位本身。如下图所示:

对于第 i + 1 i+1 i+1 位及剩余的位,因为从 0... . . . . 0...\ .... 0... .... 到 1... . . . . 1...\ .... 1... .... 必然会经过 1000 0000 1000\ 0000 1000 0000,因此按位与的结果一定为 0000 0000 0000\ 0000 0000 0000。通过上述分析可知,我们只需要找出前 i i i 位相同的部分,剩余的位置为 0 0 0 即可。
完整代码
int rangeBitwiseAnd(int left, int right) {int ans = 0;int pos = 1 << 30;while (pos > 0 && ((left & pos) == (right & pos))) {ans |= (left & pos);pos >>= 1;}return ans;
}
其中变量 p o s \mathrm{pos} pos 从高位到低位,逐位比较 l e f t \mathrm{left} left 和 r i g h t \mathrm{right} right 是否相同。
相关文章:

LeetCode 面试经典 150 题 | 位运算
目录 1 什么是位运算?2 67. 二进制求和3 136. 只出现一次的数字4 137. 只出现一次的数字 II5 201. 数字范围按位与 1 什么是位运算? ✒️ 源自:位运算 - 菜鸟教程 在现代计算机中,所有数据都以二进制形式存储,…...

postMessage 收到消息类型 “webpackWarnings“
场景描述: 当A系统中的parent页面使用iframe内嵌C系统的child页面,并且在parent页面中通过postMessageg给child页面发送消息时,如果C系统中使用了webpack,则webpack也会给child页面发送消息 ,消息类型为webpackWarnings。那么如何…...

计算机基础(day1)
1.什么是内存泄漏?什么是内存溢出?二者有什么区别? 2.了解的操作系统有哪些? Windows,Unix,Linux,Mac 3. 什么是局域网,广域网? 4.10M 兆宽带是什么意思?理论…...

cesium添加流动线
1:新建Spriteline1MaterialProperty.js文件 import * as Cesium from cesium;export function Spriteline1MaterialProperty(duration, image) {this._definitionChanged new Cesium.Event();this.duration duration;this.image image;this._time performance.…...

使用java自带的队列进行存取数据ArrayBlockingQueue 多线程读取ExecutorService
场景: 防止接收数据时处理不过来导致阻塞,使用ArrayBlockingQueue队列存储数据后,以多线程的方式处理数据 保证系统性能。 package com.yl.demo.main4;import java.text.SimpleDateFormat; import java.util.Date; import java.util.concurr…...

【音视频之SDL2】Windows配置SDL2项目模板
文章目录 前言 SDL2 简介核心功能 Windows配置SDL2项目模板下载SDL2编译好的文件VS配置SDL2 测试代码效果展示 总结 前言 在开发跨平台的音视频应用程序时,SDL2(Simple DirectMedia Layer 2)是一个备受欢迎的选择。SDL2 是一个开源库&#x…...

JavaScript 里的深拷贝和浅拷贝
JavaScript 里的深拷贝和浅拷贝 JS中数据类型分为基本数据类型和引用数据类型。 基本类型值指的是那些保存在栈内存中的简单数据段。包含Number,String,Boolean,Null,Undefined ,Symbol。 引用类型值指的是那些保存…...

Oracle基础-集合
集合:两个结果集的字段个数和字段类型必须相同,才能使用集合操作。 --UNION 并集 重复行会去重 (SELECT A,B FROM DUAL UNION SELECT C,D FROM DUAL) UNION (SELECT A,B FROM DUAL UNION SELECT E,F FROM DUAL ); --UNION ALL 全集 包含所有记录 不去重…...

《浅谈如何培养树立正确的人工智能伦理观念》
目录 摘要: 一、引言 二、《机械公敌》的情节与主题概述 三、人工智能伦理与法律问题分析 1.伦理挑战 2.法律问题 四、培养正确的人工智能伦理观念的重要性 五、培养正确的人工智能伦理观念的途径与方法 1.加强教育与宣传 2.制定明确的伦理准则和规范 3.…...
uniapp实现局域网(内网)中APP自动检测版本,弹窗提醒升级
uniapp实现局域网(内网)中APP自动检测版本,弹窗提醒升级 在开发MES系统的过程中,涉及到了平板端APP的开发,既然是移动端的应用,那么肯定需要APP版本的自动更新功能。 查阅相关资料后,在uniapp的…...
)
【Golang 面试 - 进阶题】每日 3 题(六)
✍个人博客:Pandaconda-CSDN博客 📣专栏地址:http://t.csdnimg.cn/UWz06 📚专栏简介:在这个专栏中,我将会分享 Golang 面试中常见的面试题给大家~ ❤️如果有收获的话,欢迎点赞👍收藏…...
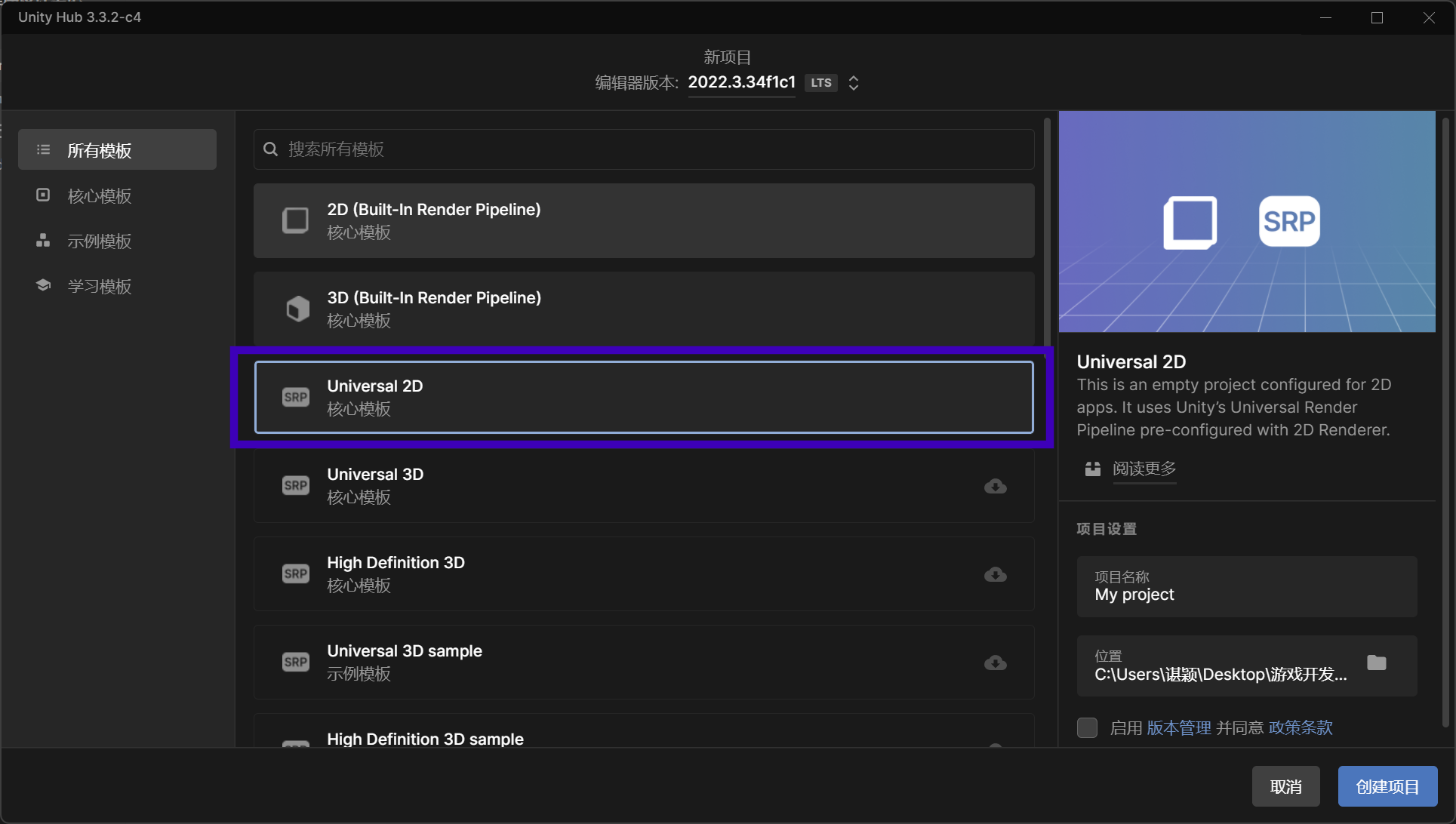
Unity横板动作游戏 -项目准备
项目准备 这是一篇 Unity 2022 最新稳定版本的教程同步笔记,本文将会讲解一些开始学习必须的条件。 安装环境 首先是安装 UnityHub,然后在 UnityHub 中安装 Unity 的版本(2022)。 只需要安装 开发者工具 和文档即可,导出到其他平台的工具等…...

基于Gunicorn + Flask + Docker的高并发部署策略
标题:基于Gunicorn Flask Docker的高并发部署策略 引言 随着互联网用户数量的增长,网站和应用程序需要能够处理越来越多的并发请求。Gunicorn 是一个 Python WSGI HTTP 服务器,Flask 是一个轻量级的 Web 应用框架,Docker 是一…...

jdk版本管理利器-sdkman
1.什么是sdkman? sdkman是一个轻量级、支持多平台的开源开发工具管理器,可以通过它安装任意主流发行版本(例如OpenJDK、Kona、GraalVM等等)的任意版本的JDK。通过下面的命令可以轻易安装sdkman: 2.安装 curl -s "https://…...

Kafka知识总结(事务+数据存储+请求模型+常见场景)
文章收录在网站:http://hardyfish.top/ 文章收录在网站:http://hardyfish.top/ 文章收录在网站:http://hardyfish.top/ 文章收录在网站:http://hardyfish.top/ 事务 事务Producer保证消息写入分区的原子性,即这批消…...

C#中重写tospring方法
在C#中,重写ToString方法允许你自定义对象的字符串表示形式。当你想要打印对象或者在调试时查看对象的状态时,重写ToString方法非常有用。 默认情况下,ToString方法返回对象的类型名称。通过重写这个方法,你可以返回一个更有意义…...

【机器学习基础】机器学习的数学基础
【作者主页】Francek Chen 【专栏介绍】 ⌈ ⌈ ⌈Python机器学习 ⌋ ⌋ ⌋ 机器学习是一门人工智能的分支学科,通过算法和模型让计算机从数据中学习,进行模型训练和优化,做出预测、分类和决策支持。Python成为机器学习的首选语言,…...

fastapi之零
FastAPI 详细介绍 FastAPI 是一个现代、快速(高性能)的 web 框架,用于构建 API。它基于标准的 Python 类型提示,使用 Starlette 作为 web 框架,Pydantic 进行数据验证和解析。以下是对 FastAPI 的详细介绍,…...

SpringBoot整合PowerJob 实现远程任务
PowerJob介绍 PowerJob 是全新一代分布式任务调度和计算框架,提供了可视化界面,可通过单机、远程等形式调用任务并提供了运行监控和日志查看的功能模块,是当前比较流行的分布式定时任务框架之一; PowerJob 官网文档地址 环境搭建…...

【扒模块】DFF
图 医学图像分割任务 代码 import torch import torch.nn as nnfrom timm.models.layers import DropPath # 论文:D-Net:具有动态特征融合的动态大核,用于体积医学图像分割(3D图像任务) # https://arxiv.org/abs/2403…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
