SPSSAU | 最好最差权重BWM原理及案例实操分析
BWM(best-worse-method,最好最差法)是一种多准则决策方法,由Jafar Rezaei于2015年提出,其通常用于确定决策标准的权重。其原理是比如5个指标,如果以前AHP就需要5个指标两两的相对重要性数据。但是现在简化为先得到‘最优’和‘最差’这2个指标。得到后需要得到BO(Best-to-other)和OW(Others-to-worst)数据,BO表示‘最好指标与各指标’的相对重要性,OW表示‘各指标与最差指标’的相对重要性。那么5个指标BO就5个数字,OW也5个数字。共10个数字就好了。
得到后使用数学求解规则那套东西来求解,其求解规划数学表达式如下:

Wbest表示最好指标的权重,Wworse表示最差指标的权重,Wj表示某指标权重,cBj表示第j个指标BO时的数据,cWj表示第j个指标OW时的数据,ε(eps)为误差,通常情况下希望该误差越小越好,越接近0越好(其实际意义为规划求解得到和实际情况的gap值)。从上述来看其思想是:本属于该重要性位置的指标,它也应该属于该重要的位置,这是BWM权重的思想意会。
最好最差权重BWM案例
1 背景
当前有一份数据需要进行BWM权重计算,其BO数据和OW数据如下:

BO数据表示‘最好指标与各指标’的相对重要性,比如上表格中指标2对应的BO数据为1,其意味着‘最好指标与指标2’的重要程度为2,至于2代表的意义,其由标度决定(通常情况下使用1 ~ 9级标度较多即1分最不重要,9分最重要,如果是这样则意味着‘最好指标’相对于指标2来讲,重要性很弱,也即说明指标2很重要的意思);
others-to-worst(OW)表示‘各指标与最差指标’的相对重要性,比如上表格中指标2对应的OW数据为8,其意味着‘指标2与最差指标’的相对重要性为8,如果8代表很重要,那么意味着‘指标2’相对于‘最差指标’,指标2很重要。
2 理论
针对BWM权重法,其一般的步骤如下:
- 确定好研究的指标即准则指标;
- 确定最优准则和最劣准则,即最优和最劣指标
- 确定好使用的标度,比如使用1~9分法,1分表示最差,9分表示最差;
- 在确认好指标、最优和最劣指标及标度后,准备好分析数据即BO数据和OW数据;
- 利用数学规划求解计算出权重值;
- 进行一致性检验。
3 操作
本例子SPSSAU操作如下:

需要注意的是,SPSSAU提供两个表格分别放BO和OW数据。以及如果有多个专家打分,那么比如BO数据就有多行,依次放入就好。与此同时,在计算结果输出时,1个专家对应着1份权重数据,多个专家就对应多份权重数据,因此结果中还会有多个专家权重的平均值即输出global权重值。
4 SPSSAU输出结果
SPSSAU共输出5个表格和1个权重分布图,如下说明。
| 表格 | 说明 |
|---|---|
| BO和OW值 | 即放入的原始数据BO和OW数据 |
| BWM权重结果 | 展示BWM法计算得到的权重 |
| Consistency Index(CI)表格 | 展示一致性指数CI值 |
| BWM一致性检验结果 | 展示CR指标及一致性检验结果 |
5文字分析

上表格展示BO和OW数据,即原始输入数据。事实上BWM权重计算时,其前期准备工作包括准备好准则指标,确定最优和最劣指标,确定好标度,然后让专家进行打分,专家打分数据才得到最终的BO和OW数据。

BWM权重计算的原理是数学规划求解,其核心目的是让‘让本应该某指标所属地位,就让其在该位置’,意思是本来该项重要那么其权重就应该高,本来某项不重要那么其权重就应该低。并且这种gap(即数学规划里面的eps指标)应该尽可能小。

上表格展示一致性系数Consistency Index;CI指标为固定值,当前最多为9阶数据,CI指标是接下来CR指标的计算中间值,其为中间过程值并不特别意义。

上表格展示一致性检验及其结果等。上表格展示EPS指标,EPS是BWM进行数学规划求解时计算得到。CI值是查表得到,比如当前是5个专家打分数据,那么对应为2.3。一致性比率CR指标用于评价一致性,CR=EPS指标/CI值,并且对CR进行检验的标准为0.5,如果小于0.5则意味着通过一致性检验,反之则说明没有通过一致性检验。本次数据计算得到CR值为0.005,即通过一致性检验,意味着专家打分数据相对重要性满足一致性,并没有逻辑性问题。
如果没有通过一致性检验,需要考虑是否有出现比如指标1相对指标2更加重要,指标2比起指标3更加重要,那么肯定指标1相对指标3更重要,但数据上却出现指标3比指标1更重要。
6 剖析
涉及以下几个关键点,分别如下:
- 请确保分别放入BO和OW数据,并且如果有多个专家,那么对应就有多行BO或者OW数据。
- BWM的计算参考文献如下:Rezaei J .Best-worst multi-criteria decision-making method: Some properties and a linear model[J].Omega, 2016, 64(oct.):126-130.DOI:10.1016/j.omega.2015.12.001.
7 疑难解惑
- BWM权重计算时一致性检验没有通过?
如果没有通过一致性检验,需要考虑是否有出现比如指标1相对指标2更加重要,指标2比起指标3更加重要,那么肯定指标1相对指标3更重要,但数据上却出现指标3比指标1更重要。
相关文章:

SPSSAU | 最好最差权重BWM原理及案例实操分析
BWM(best-worse-method,最好最差法)是一种多准则决策方法,由Jafar Rezaei于2015年提出,其通常用于确定决策标准的权重。其原理是比如5个指标,如果以前AHP就需要5个指标两两的相对重要性数据。但是现在简化为…...
docker安装elasticsearch(es)最新版本
docker安装elasticsearch(es) docker官网 https://hub.docker.com/ https://www.cnblogs.com/balloon72/p/13177872.html 1、拉取最新项目elasticsearch docker pull elasticsearch:8.14.3lscpu 查看架构 2、构建环境 mkdir -p /data/elasticsear…...

02 RabbitMQ:下载安装
02 RabbitMQ:下载&安装 1. 下载&安装1.1. 官网1.2. Docker方式1.2.1. 下载镜像1.2.2. 启动1.2.3. 登录验证 1. 下载&安装 1.1. 官网 RabbitMQ: One broker to queue them all | RabbitMQ 1.2. Docker方式 1.2.1. 下载镜像 # docker pull 镜像名称[…...

mmcv库出现No module named ‘mmcv._ext
遇到 "No module named mmcv._ext" 这个错误通常意味着你的 Python 环境中缺少 mmcv 库的扩展模块 _ext。mmcv(MMDetection 训练工具箱的核心库)通常依赖于 _ext 模块来提供一些高性能的操作,这些操作是用 C/C 实现的,并…...
)
防止xss(跨站脚本攻击)
1、输出数据时进行转义:这是最基本的预防措施。确保在输出数据到HTML时对特殊字符进行适当的转义,以防止它们被解释为HTML或JavaScript代码。PHP中可以使用htmlspecialchars()、strip_tags()、htmlentities函数来实现这一点。 echo htmlspecialchars($d…...

django小型超市库存与销售管理系统-计算机毕业设计源码46608
摘 要 随着信息技术的快速发展,超市库存与销售管理面临着前所未有的挑战与机遇。为了提升超市的运营效率,优化库存管理,并增强销售数据的分析能力,我们基于Django框架设计并开发了一套小型超市库存与销售管理系统。该系统充分利用…...

项目实战_表白墙(简易版)
你能学到什么 一个比较简单的项目:表白墙(简易版),浏览器:谷歌升级版将在下个博客发布 效果如下 正文 说明 我们是从0开始一步一步做这个项目的,里面的各种问题,我也会以第一人称视角来解…...

优化 Spring Boot 项目启动速度:高效管理大量 Bean 注入
个人名片 🎓作者简介:java领域优质创作者 🌐个人主页:码农阿豪 📞工作室:新空间代码工作室(提供各种软件服务) 💌个人邮箱:[2435024119@qq.com] 📱个人微信:15279484656 🌐个人导航网站:www.forff.top 💡座右铭:总有人要赢。为什么不能是我呢? 专栏导…...

《LeetCode热题100》---<5.普通数组篇六道>
本篇博客讲解LeetCode热题100道普通数组篇中的六道题 第一道:最大子数组和(中等) 第二道:合并区间(中等) 第一道:最大子数组和(中等) 法一:贪心算法 class So…...

【Hot100】LeetCode—169. 多数元素
目录 题目1- 思路2- 实现⭐169. 多数元素——题解思路 3- ACM 实现 题目 原题连接:169. 多数元素 1- 思路 定义两个变量 一个是 count:维护当前元素的出现次数一个是 ret :维护当前元素 思路 遍历整个数组**①如果 count 0 **ÿ…...

专科、本科、研究生是按照什么分类的?
高等教育按照阶段主要分为以下几类 一、专业学位教育 特点:职业导向 专业学位教育是针对特定职业领域的专业培训,如医学、法律、工程等,旨在使学生具备从事相关职业所需的专业知识和实践技能。 实践性 专业学位教育注重实践教学和职业技…...

关于实时ODS层数仓搭建的三个问题
目录 问题一:数据同步的实时性无法满足 问题二:批量数据同步计算处理效率低 问题三:没有稳定的数据传输管道 FineDataLink的解决方案 实战案例-销售部门与财务部门数据同步 设置ODS层实时同步任务 设置DW层增量数据同步 设置 DM 层任务汇总 关…...

微信仿H5支付是什么
仿H5支付是指一种模拟原生H5支付流程的非官方支付方式。这种支付方式通常是由第三方支付服务提供商开发和维护的,目的是为了绕过官方支付渠道的限制,如费率、审核等问题。然而,由于仿H5支付并非官方授权和认可的支付方式,其安全性…...

网络安全知识竞赛规则及流程方案
为普及网络安全知识,进一步提升网络安全意识,树立正确的网络安全观,营造安全健康文明的网络环境,在2023年国家网络安全宣传周到来之际,特举办网络安全知识有奖竞赛活动,通过竞赛活动普及国家法律法规、政策…...

赞!蚓链用数字化打造助农扶农电商平台!
助农扶农电商平台在推动农村经济发展、促进农民增收方面发挥着重要作用。蚓链数字化平台使用“防伪溯源”为农户、商户、平台、政府与消费者打造了全方位的信任链条和纽带。给各方带来众多价值! (一)农户方面 1、拓宽销售渠道,降…...

RocketMQ延时消息
RocketMQ消息发送基本示例(推送消费者)-CSDN博客 RocketMQ消费者主动拉取消息示例-CSDN博客 RocketMQ顺序消息-CSDN博客 RocketMQ广播消息-CSDN博客 延时消息: 延时消息实现的效果就是产者调用 producer.send 方法后,消息会立即发送到 Broker,并被存…...

【C++/STL】:哈希的应用 -- 位图布隆过滤器
目录 🚀🚀前言一,位图1. 位图的概念2. STL库中的位图3. 位图的设计4. 位图的模拟实现5. 位图的优缺点6. 位图相关考察题⽬ 二,布隆过滤器1. 布隆过滤器的概念2. 布隆过滤器的实现3. 布隆过滤器删除问题4. 布隆过滤器的优缺点 点击…...
非线性面板数据实证模型及 Stata 具体操作步骤
目录 一、引言 二、文献综述 三、理论原理 四、实证模型 五、稳健性检验 六、程序代码及解释 一、引言 在当今的经济和社会研究中,非线性面板数据模型的应用日益广泛。这类模型能够更好地捕捉数据中的复杂关系,为研究者提供更深入和准确的分析结果。…...

视角 | 麻省理工学院提出出温度计校准法,专治AI大模型过度自信
在数字化浪潮的推动下,人工智能(AI)正成为塑造未来的关键力量。硅纪元视角栏目紧跟AI科技的最新发展,捕捉行业动态;提供深入的新闻解读,助您洞悉技术背后的逻辑;汇聚行业专家的见解,…...
昇思25天学习打卡营第XX天|CycleGAN图像风格迁移互换
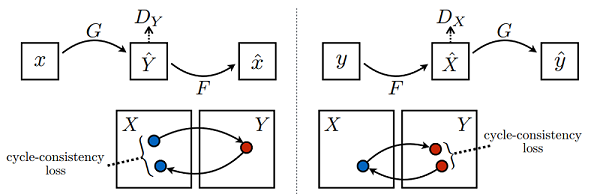
CycleGAN是一种用于图像到图像翻译的生成对抗网络,它突破了传统域迁移模型的限制,无需成对样本即可学习图像在不同域间的转换。这种无监督的方法特别适用于难以获取配对数据的场景,例如艺术风格迁移。与需要成对训练样本的Pix2Pix不同&#x…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...

GraphQL 实战篇:Apollo Client 配置与缓存
GraphQL 实战篇:Apollo Client 配置与缓存 上一篇:GraphQL 入门篇:基础查询语法 依旧和上一篇的笔记一样,主实操,没啥过多的细节讲解,代码具体在: https://github.com/GoldenaArcher/graphql…...

ZYNQ学习记录FPGA(一)ZYNQ简介
一、知识准备 1.一些术语,缩写和概念: 1)ZYNQ全称:ZYNQ7000 All Pgrammable SoC 2)SoC:system on chips(片上系统),对比集成电路的SoB(system on board) 3)ARM:处理器…...
