【每日一题】【最短路】【BFS】小红走矩阵 “葡萄城杯”牛客周赛 Round 53 F题 C++
“葡萄城杯”牛客周赛 Round 53 F题
小红走矩阵
题目背景
“葡萄城杯”牛客周赛 Round 53
题目描述
n × m n\times m n×m的矩阵由障碍和空地组成,初始时小红位于起点 ( 1 , 1 ) (1,1) (1,1),她想要前往终点 ( n , m ) (n,m) (n,m)。小红每一步可以往上下左右四个方向的空地移动一格。
小红在起点处可以进行最多一次操作:选择矩阵中的一处障碍替换为空地,但代价是小红必须选择失去向上下左右四个方向中一个移动的能力。
求小红从起点到达终点的最小步数,如果无法到达则输出 − 1 -1 −1
输入格式
第一行输入两个整数 n , m ( 1 ≤ n , m ≤ 1000 ) n, m(1\le n ,m \le 1000) n,m(1≤n,m≤1000)代表矩阵的大小。
此后 n n n 行,每行输入 m m m个字符 a 1 a 2 . . . a n ( a i ∈ { ′ X ′ , ′ . ′ } ) a_1a_2...a_n(a_i\in{\{'X','.'\}}) a1a2...an(ai∈{′X′,′.′})描述矩阵中这一行的情况,其中 ′ X ′ 'X' ′X′(Ascii:88)代表障碍, ′ . ′ '.' ′.′(Ascii:46)代表空地。保证起点和终点都是空地
输出格式
在一行上输出一个整数,表示小红从起点到达终点的最小步数;如果无论怎么操作都无法到达,则直接输出 − 1 -1 −1
样例 #1
样例输入 #1
4 4
..X.
XXX.
.X..
.X..
样例输出 #1
6
说明
小红失去向上走的能力,消除 ( 1 , 3 ) (1,3) (1,3)处障碍,从起点到终点的最小步数为 6 6 6。
样例 #2
样例输入 #2
4 4
.XX.
XXX.
.X..
.X..
样例输出 #2
-1
说明
小红最多只能删除一个障碍,无法到达终点。
做题要点
- 起点处可以进行最多一次操作
- 选择失去向上下左右四个方向中一个移动的能力
- 最短路
- n , m ( 1 ≤ n , m ≤ 1000 ) n, m(1\le n ,m \le 1000) n,m(1≤n,m≤1000)
做题难点
没处理好删除一个障碍和不删除障碍的最短路关系。
如果混在一起都记为到当前格子最短路。
那么就可能出现情况有删除障碍提前到达更新了最短路,导致不删除障碍后达的无法更新最短路并加入后续bfs中,但后续又有障碍,因为只能删除一个障碍,就会导致本来有解变无解。
做题思路
这道题为典型的最短路变种问题,通常使用方法为广度优先搜索(BFS)。
首先如果不考虑失去一个方向移动能力和删除操作。
普通的跑一次BFS,可记为第一种答案。
BFS基本套路为:
- 初始化队列和标记数组(花费数组),将起点加入队列
- 取队列元素并出队,根据当前元素进行下一步行走(判断+更新+入队)
- 重复第二步直到队列为空
还有就是禁掉(ban)一个移动能力然后再跑一次BFS,这次加入可以穿越障碍一次的判断即可。
因为有四个方向,所以跑四次BFS。
重点在于如何处理好删除一个障碍和不删除障碍的最短路关系。
如果设的是花费数组那么二维的数组 c n t i , j cnt_{i,j} cnti,j是不够的,因为二维的记录当前坐标的最短路,可能会产生删除障碍到 ( i , j ) (i,j) (i,j)的最短路为 k k k,而不删除障碍到 ( i , j ) (i,j) (i,j)的最短路为 k + a k+a k+a, a ≥ 1 a \ge 1 a≥1,然后从 ( i , j ) (i,j) (i,j)到终点还有障碍(必须穿过),就会导致在前面就用掉了这次删除障碍的机会。后面不删除的因为最短路并不是最短的无法继续入队执行BFS导致最后答案为无解。
如果额外想办法以消耗时间的方法去解决,很容易导致TLE(超时)
这里就需要用额外空间的方法去解决,设三维数组 c n t i , j , k cnt_{i,j,k} cnti,j,k其中第三维大小为2,即布尔下标,其中 k = t r u e / 1 k=true/1 k=true/1时候表示为从起点到 ( i , j ) (i,j) (i,j)的没消耗删除障碍次数的最短路,
反之 k = f a l s e / 0 k=false/0 k=false/0时候表示为从起点到 ( i , j ) (i,j) (i,j)的消耗删除障碍次数的最短路。
最后本次到终点的最短路取两者的最小值即可。
总结思路
- 普通BFS一次
- ban掉四个方向各一次并跑BFS
- 取所以答案的最短路最小值
核心代码对应思路
ban掉四个方向各一次并跑BFS
bfs();
for(int i=0;i<4;i++){memset(cnt,0x3f,sizeof(cnt));//重置花费数组memset(cut,true,sizeof(cut));//重置禁止数组cut[i] = false;//ban掉该方向bfs2();
}
处理好删除一个障碍和不删除障碍的最短路关系
if(a[nx][ny] == '.' && cnt[nx][ny][have] > cnt[x][y][have] + 1){cnt[nx][ny][have] = cnt[x][y][have] + 1;q.push(make_tuple(nx,ny,have));}else if(a[nx][ny] == 'X' && have && cnt[nx][ny][false] > cnt[x][y][have] + 1){cnt[nx][ny][false] = cnt[x][y][have] + 1;//!!!q.push(make_tuple(nx,ny,false));}
时间复杂度分析
相当于跑五次BFS为 O ( 5 n × m ) O(5n\times m) O(5n×m)
伪代码

代码
#include <iostream>
#include <vector>
#include <queue>
#include <deque>
#include <tuple>
#include <map>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1e3+10;
const int INF = 0x3f3f3f3f;
const long long LNF = 0x3f3f3f3f3f3f3f3f;
int n,m,ans = INF;
char a[N][N];
int cnt[N][N][2];
int bt[4][2] = {{0,1},{1,0},{0,-1},{-1,0}};
bool cut[4];
void init(){cin >> n >> m;//for(int i=1;i<=n;i++)cin >> a[i];//for(int i=1;i<=n;i++)a[i] = " " + a[i];memset(cnt,0x3f,sizeof(cnt));for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)cin >> a[i][j];
}
inline bool check(int x,int y){return x>=1 && x<=n && y>=1 && y<=m;
}
void bfs(){int x,y,nx,ny;queue<pair<int,int> > q;cnt[1][1][0] = 0;q.push(make_pair(1,1));while(!q.empty()){tie(x,y) = q.front();q.pop();for(int i=0;i<4;i++){nx = x + bt[i][0];ny = y + bt[i][1];if(check(nx,ny) && a[nx][ny] == '.' && cnt[nx][ny][0] > cnt[x][y][0] + 1){cnt[nx][ny][0] = cnt[x][y][0] + 1;q.push(make_pair(nx,ny));}}}ans = min(ans,cnt[n][m][0]);
}
void bfs2(){int x,y,nx,ny;bool have;queue<tuple<int,int,bool> > q;cnt[1][1][1] = 0;q.push(make_tuple(1,1,true));while(!q.empty()){tie(x,y,have) = q.front();q.pop();for(int i=0;i<4;i++){if(!cut[i])continue;nx = x + bt[i][0];ny = y + bt[i][1];if(check(nx,ny)){if(a[nx][ny] == '.' && cnt[nx][ny][have] > cnt[x][y][have] + 1){cnt[nx][ny][have] = cnt[x][y][have] + 1;q.push(make_tuple(nx,ny,have));}else if(a[nx][ny] == 'X' && have && cnt[nx][ny][false] > cnt[x][y][have] + 1){cnt[nx][ny][false] = cnt[x][y][have] + 1;q.push(make_tuple(nx,ny,false));}}}}ans = min({ans,cnt[n][m][false],cnt[n][m][true]});
}
int main(){init();bfs();for(int i=0;i<4;i++){memset(cnt,0x3f,sizeof(cnt));memset(cut,true,sizeof(cut));cut[i] = false;bfs2();}if(ans == INF)cout << -1;else cout << ans;return 0;
}
相关文章:

【每日一题】【最短路】【BFS】小红走矩阵 “葡萄城杯”牛客周赛 Round 53 F题 C++
“葡萄城杯”牛客周赛 Round 53 F题 小红走矩阵 题目背景 “葡萄城杯”牛客周赛 Round 53 题目描述 n m n\times m nm的矩阵由障碍和空地组成,初始时小红位于起点 ( 1 , 1 ) (1,1) (1,1),她想要前往终点 ( n , m ) (n,m) (n,m)。小红每一步可以往上…...

无线磁吸充电宝哪个牌子值得入手?什么牌子磁吸充电宝性价比高?
在当下科技日新月异的时期,无线磁吸充电宝成为了众多电子设备用户的得力助手。然而,面对市场上众多品牌和型号的无线磁吸充电宝,消费者常常陷入选择的困境:到底哪个牌子值得入手?什么牌子的磁吸充电宝性价比高…...
)
互联网摸鱼日报(2024-08-01)
互联网摸鱼日报(2024-08-01) 36氪新闻 氪星晚报 | Uber与比亚迪合作,将在平台上增加10万辆电动汽车;维维股份将收购大窑汽水?公司回应:消息不实;我国科学家取得全固态锂电池研究新突破 《死侍与金刚狼》,…...
Alpla003经典的价量背离的因子在可转债列表里的因子分析(附python代码)
原创文章第605篇,专注“AI量化投资、世界运行的规律、个人成长与财富自由"。 遗传算法给出的因子五花八门,可解释性不高。 强化学习原理不同,但结果类似。 大模型之前咱们尝试过,Quantlab3.9代码:内置大模型LL…...

进阶理解——typeof 、instanceof
typeof 、instance of 先聊聊JavaScript基本类型数据类型5种含值数据类型2种不含值类型 6种类型的*对象* typeofinstanceof总结进一步扩展一下具体讨论一下typeof局限性扩展判断方法 很多时候,回头望,理解会更深刻,也希望能帮助一些初学的同学…...
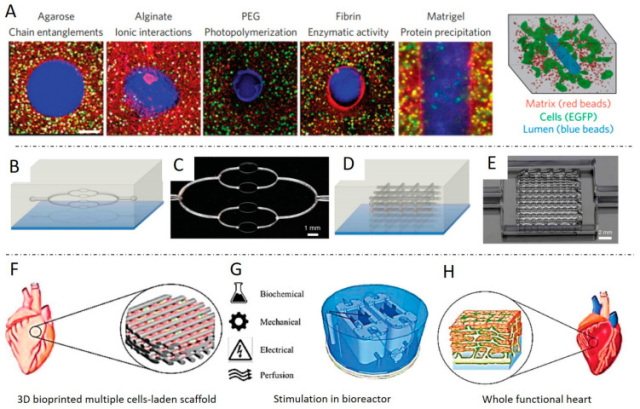
不同类型的生物反应器在支架成熟过程中具有哪些特点和应用?
3D Bioprinting of Human Tissues: Biofabrication, Bioinks, and Bioreactors是发表于《International Journal of Molecular Sciences》的一篇综述,详细介绍了3D生物打印人体组织的相关技术进展,包括数据处理、生物打印技术、生物墨水配方、生物反应器…...

8. Spring Ai之入门到精通(超级详细)
简介 2024年5月30号Spring AI 的 1.0.0 里程碑 1 版本发布。表明版本已正在巩固,并且大部分主要错误和问题已经解决,API基本已确定,不会发生很大的变化。 在与大模型集成方面,继LangChain4j之后,又一重大的框架诞生。标…...

寄存器和硬件的关系
寄存器也是一种存储器,只不过普通的存储器只能写和读。里面的数据并没有赋予什么实际意义。但是寄存器就不一样了,寄存器的每一位数据,都对应了硬件电路的状态。寄存器和外设的硬件电路,是可以进行互动的。所以,程序到…...

【WEB】ctfshow-萌新-web9-15
文章目录 题目介绍:题目分析:payload: 题目介绍: ctfshow-萌新计划-web9-15 <?php # flag in config.php include("config.php"); if(isset($_GET[c])){$c $_GET[c];if(preg_match("/system|exec|highlight…...

【Vulnhub靶场AI-WEB-1.0打靶教程】
第一步:查看虚拟机的ip 第二步:扫描ip下开放的80端口 第三步:扫描查到的ip地址下的目录 第四步:访问查到的目录 访问robot.txt 第五步:访问robot.txt显示出的目录 第六步:打开kali终端,使用sqlmap功能 sq…...

html实现酷炫美观的可视化大屏(十种风格示例,附源码)
文章目录 完整效果演示1.蓝色流线风的可视化大屏1.1 大屏效果1.2 大屏代码1.3 大屏下载 2.地图模块风的可视化大屏2.1 大屏效果2.2 大屏代码2.3 大屏下载 3.科技轮动风的可视化大屏3.1 大屏效果3.2 大屏代码3.3 大屏下载 4.蓝色海洋风的可视化大屏4.1 大屏效果4.2 大屏代码4.3 …...

【C++BFS算法 二分查找】2812. 找出最安全路径
本文涉及知识点 CBFS算法 C二分查找 LeetCode2812. 找出最安全路径 给你一个下标从 0 开始、大小为 n x n 的二维矩阵 grid ,其中 (r, c) 表示: 如果 grid[r][c] 1 ,则表示一个存在小偷的单元格 如果 grid[r][c] 0 ,则表示一…...

轻触开关 KH-4.5X4.5X5.5H-STM
品 牌: kinghelm(金航标) 厂家型号: KH-4.5X4.5X5.5H-STM 封装: SMD 商品毛重: 0.317克(g) 包装方式: 编带...

3.redis客户端
1.命令行客户端 在安装redis的时候就已经安装好了,就是redis-cli redis-cli -h 127.0.0.1 -p 6379 -a 123456 -a 表示密码 -h 表示ip,不配置默认为本机 127.0.0.1 -p 表示端口,不配置默认为 6379 进入后可以输入ping,返回pong代表…...

Rust配置国内源,解决安装依赖慢问题
温馨提示:最新内容仅在原文更新。 国内源使用字节的RsProxy https://rsproxy.cn/ 解决rust-analyzer加载时间过长(请参考本文) 配置环境变量 Mac export RUSTUP_DIST_SERVER"https://rsproxy.cn" export RUSTUP_UPDATE_ROOT"https://rsproxy.cn/r…...

AI学习指南机器学习篇- Q学习的参数与调优
AI学习指南机器学习篇- Q学习的参数与调优 在强化学习领域中,Q学习是一种经典的算法,可以用来解决各种问题,包括游戏和机器人控制等。Q学习算法的性能很大程度上取决于一些重要的参数,例如学习率和折扣因子。本文将介绍这些参数的…...

《小迪安全》学习笔记02
域名默认存放目录和IP默认存放目录不一样。 IP地址是WWW文件里的,域名访问是WWW里的一个子目录里的(比如是blog)。 Nmap: Web源码拓展 拿到一个网站的源码,要分析这几个方面↑。 不同类型产生的漏洞类型也不一样 在网站中&…...

C语言:自定义类型进阶(结构体、联合体、枚举)
自定义类型(结构体、联合体、枚举) 一、结构体(一)结构体的内存对齐1、结构体内存对齐规则(1)引子(2)offsetof 宏函数(3)内存对齐原理(4ÿ…...

SPSSAU | 最好最差权重BWM原理及案例实操分析
BWM(best-worse-method,最好最差法)是一种多准则决策方法,由Jafar Rezaei于2015年提出,其通常用于确定决策标准的权重。其原理是比如5个指标,如果以前AHP就需要5个指标两两的相对重要性数据。但是现在简化为…...
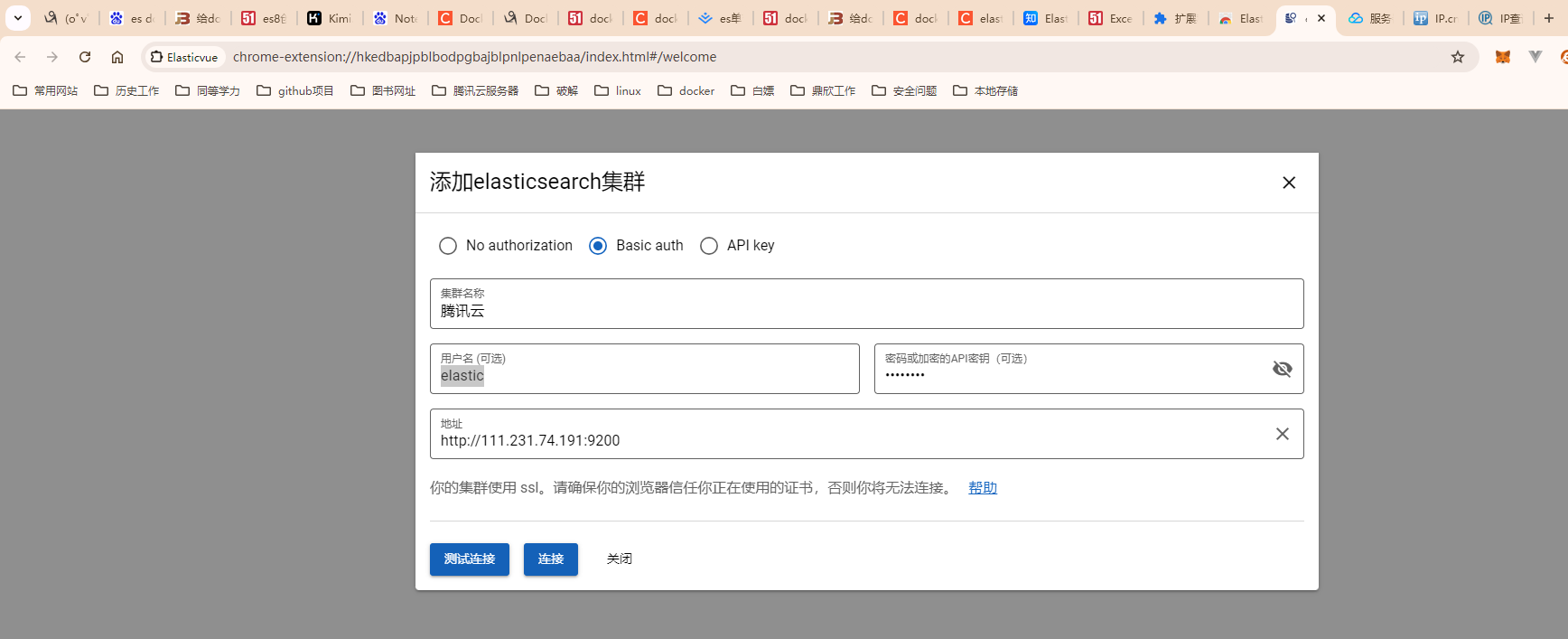
docker安装elasticsearch(es)最新版本
docker安装elasticsearch(es) docker官网 https://hub.docker.com/ https://www.cnblogs.com/balloon72/p/13177872.html 1、拉取最新项目elasticsearch docker pull elasticsearch:8.14.3lscpu 查看架构 2、构建环境 mkdir -p /data/elasticsear…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...

Python网页自动化Selenium中文文档
1. 安装 1.1. 安装 Selenium Python bindings 提供了一个简单的API,让你使用Selenium WebDriver来编写功能/校验测试。 通过Selenium Python的API,你可以非常直观的使用Selenium WebDriver的所有功能。 Selenium Python bindings 使用非常简洁方便的A…...

Sklearn 机器学习 缺失值处理 获取填充失值的统计值
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 使用 Scikit-learn 处理缺失值并提取填充统计信息的完整指南 在机器学习项目中,数据清…...

AT模式下的全局锁冲突如何解决?
一、全局锁冲突解决方案 1. 业务层重试机制(推荐方案) Service public class OrderService {GlobalTransactionalRetryable(maxAttempts 3, backoff Backoff(delay 100))public void createOrder(OrderDTO order) {// 库存扣减(自动加全…...
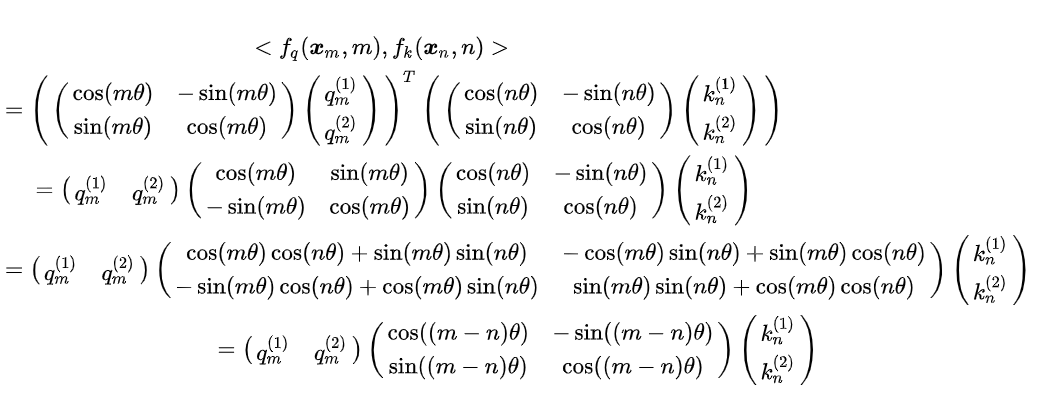
多模态学习路线(2)——DL基础系列
目录 前言 一、归一化 1. Layer Normalization (LN) 2. Batch Normalization (BN) 3. Instance Normalization (IN) 4. Group Normalization (GN) 5. Root Mean Square Normalization(RMSNorm) 二、激活函数 1. Sigmoid激活函数(二分类&…...
