程序员面试题------N皇后问题算法实现
N皇后问题是一个著名的计算机科学问题,它要求在N×N的棋盘上放置N个皇后,使得它们之间不能相互攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上。这个问题可以看作是一个回溯算法问题,通过逐步尝试不同的放置位置,并在发现不满足条件时回溯到上一步,来找到所有可能的解。
以下是解决N皇后问题的详细解题思路:
- 初始化棋盘:创建一个N×N的棋盘,通常使用一个二维数组来表示,初始化所有位置为空,即没有放置任何皇后。
- 选择位置:从棋盘的第一行开始,尝试在每一行中选择一个位置放置一个皇后。由于棋盘是N×N的,因此每一行都有N个可能的放置位置。
- 检查冲突:在选择了一个位置后,需要检查该位置是否与其他已经放置的皇后冲突。这包括检查同一列、两条对角线(一条是从左上到右下,另一条是从右上到左下)是否有冲突。如果有冲突,则说明当前放置位置不合适,需要回溯到上一步,选择另一个位置。
- 放置皇后:如果当前选择的位置没有冲突,则在该位置放置一个皇后,并标记该位置为已占用。
- 递归:在当前行放置了一个皇后后,需要继续在下一行中放置皇后。这需要重复执行选择位置、检查冲突和放置皇后的步骤,直到所有N个皇后都被放置在棋盘上。
- 回溯:如果在放置皇后的过程中发现当前选择的位置不合适(即有冲突),则需要回溯到上一步,并尝试在之前已经放置的皇后所在的行中选择一个新的位置。
- 收集解:当所有N个皇后都被放置在棋盘上且没有冲突时,得到了一个有效的解。将这个解收集起来,继续寻找下一个解。
- 结束条件:当所有可能的行都尝试过,仍然没有找到一个有效的解时,算法结束。
N皇后问题的一个关键点是回溯算法的使用。通过递归地尝试不同的放置位置,并在发现不合适时回溯,算法能够找到所有可能的解。这个过程需要仔细设计和实现,以确保能够正确地检查冲突和回溯。
N皇后问题有哪些经典算法实现?
N皇后问题有多种经典算法实现,其中最著名的是回溯算法。回溯算法通过递归地在棋盘上尝试放置皇后,并在发现冲突时回溯到上一步,以找到所有可能的解决方案。以下是几种实现N皇后问题的经典算法:
- 回溯算法:
- 回溯算法是解决N皇后问题的最直接和最常用的方法。它通过递归地在棋盘上尝试放置皇后,并在发现冲突时回溯到上一步。这种方法可以找到所有可能的解决方案。
- 位运算:
- 位运算是一种高效的方法,它使用位向量来表示棋盘上的皇后放置情况。通过位运算,可以快速判断是否有冲突,并且能够优化空间复杂度。
- 动态规划:
- 动态规划是一种将问题分解为更小子问题的方法。对于N皇后问题,可以使用动态规划来避免重复计算,从而提高算法的效率。
- 迭代算法:
- 迭代算法是一种使用循环结构而不是递归结构的算法。它通过模拟回溯过程来找到解决方案,但通常不如递归算法直观。
- 启发式算法:
- 启发式算法,如遗传算法、模拟退火等,可以在没有完全解决方案的情况下找到近似解。这些算法适用于N皇后问题的变体,如在限制条件下寻找最优解。
回溯算法是解决N皇后问题的最经典和最直接的方法,因此通常被视为标准实现。位运算和动态规划是提高算法效率的优化方法,而迭代算法和启发式算法适用于特定场景和变体。在面试或算法竞赛中,回溯算法是最常见的实现方式。
- 启发式算法,如遗传算法、模拟退火等,可以在没有完全解决方案的情况下找到近似解。这些算法适用于N皇后问题的变体,如在限制条件下寻找最优解。

来检查同一列是否有冲突,通过异或运算(XOR)来检查同一斜线上是否有冲突。
-
回溯:如果在放置皇后的过程中发现冲突,则需要回溯到上一步,并尝试在之前已经放置的皇后所在的行中选择一个新的位置。
-
收集解:当所有N个皇后都被放置在棋盘上且没有冲突时,得到了一个有效的解。将这个解收集起来,继续寻找下一个解。
位运算应用于N皇后问题的优点是能够快速判断冲突,并且只需要一个整数数组来表示整个棋盘的状态,从而优化了空间复杂度。这种方法通常比传统的回溯算法更加高效。
代码示例
以下是一个简单的 Python 代码示例,展示了如何使用回溯算法解决 N 皇后问题:
def solveNQueens(n):def is_safe(board, row, col):# Check this row on left sidefor i in range(col):if board[row][i] == 'Q':return False# Check upper diagonal on left sidefor i, j in zip(range(row, -1, -1), range(col, -1, -1)):if board[i][j] == 'Q':return False# Check lower diagonal on left sidefor i, j in zip(range(row, n, 1), range(col, -1, -1)):if board[i][j] == 'Q':return Falsereturn Truedef solve(board, col):if col >= n:return Truefor i in range(n):if is_safe(board, i, col):board[i][col] = 'Q'if solve(board, col + 1):return Trueboard[i][col] = '.' # Backtrackreturn Falseboard = [['.' for _ in range(n)] for _ in range(n)]if not solve(board, 0):return "Solution does not exist"return board
# Example usage:
n = 4
print(solveNQueens(n))
这个代码定义了一个 solveNQueens 函数,它接受一个整数 n 作为参数,表示棋盘的大小。它内部定义了一个辅助函数 is_safe 来检查是否可以在棋盘的某一位置放置一个皇后,以及一个递归函数 solve 来尝试在棋盘上放置所有皇后。最终,solveNQueens 函数返回所有可能的解决方案。
请注意,这段代码是一个简化的示例,它没有处理所有可能的边界条件和优化。在实际的面试中,面试官可能会要求你实现一个更完整和优化的版本。

相关文章:

程序员面试题------N皇后问题算法实现
N皇后问题是一个著名的计算机科学问题,它要求在NN的棋盘上放置N个皇后,使得它们之间不能相互攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上。这个问题可以看作是一个回溯算法问题,通过逐步尝试不同的放置位置…...
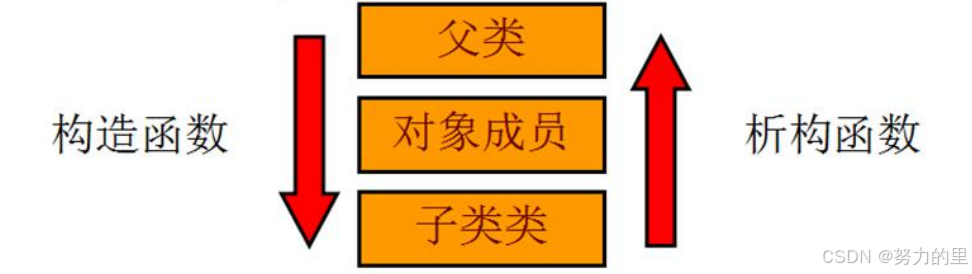
【C++学习】6、继承
1、什么是继承? 继承描述的是类与类之间的关系,A类继承B类,A类就拥有B类的数据和方法。 继承的方式: 公有继承(public) 保护继承(protected) 私有继承(private&…...
 按键与外部中断)
从零开始的MicroPython(三) 按键与外部中断
上一篇:从零开始的MicroPython(二) GPIO及点灯代码 文章目录 前言硬件原理软件原理注意代码编写轮询外部中断其他 前言 点灯是嵌入式GPIO输出的典型,按键则是输入的典型。 硬件原理 按键对角接通。 软件原理 如果是一端接高电平,一端接单…...

Windows下编译安装Kratos
Kratos是一款开源跨平台的多物理场有限元框架。本文记录在Windows下编译Kratos的流程。 Ref. from Kratos KRATOS Multiphysics ("Kratos") is a framework for building parallel, multi-disciplinary simulation software, aiming at modularity, extensibility, a…...
)
汽车-腾讯2023笔试(codefun2000)
题目链接 汽车-腾讯2023笔试(codefun2000) 题目内容 现在塔子哥有 n 个汽车,所有的汽车都在数轴上,每个汽车有1.位置 pos 2.速度 v ,它们都以在数轴上以向右为正方向作匀速直线运动。 塔子哥可以进行任意次以下操作:选择两个汽车…...

软测面试二十问(最新面试)
1.软件测试的流程是什么 参加需求评审会,解决需求疑问---写测试用例---对测试用例进行评审---评审后开始执行测试---提交bug---追踪bug---关闭bug---回归测试---交叉测试---编写测试报告---冒烟测试 2.什么是黑盒测试和白盒测试?它们有何区别 黑盒测试…...

风吸杀虫灯采用新型技术 无公害诱虫捕虫
TH-FD2S】风吸杀虫灯利用害虫的趋光性和对特定波长的光源(如紫外光、蓝光)的敏感性,通过光波引诱害虫成虫扑灯。同时,内置的风扇产生强烈的气流,形成负压区,将害虫迅速吸入到收集器中。害虫在收集器内被风干…...
)
随手记录第十二话 -- JDK8-21版本的新增特性记录(Lambda,var,switch,instanceof,record,virtual虚拟线程等)
本文主要用于记录jdk8以来的新增特性及使用方法! 1.Java8 Lambda表达式(8) 1.1 方法引用 List<String> list List.of("1", "2", "3");list.forEach(i -> System.out.println(i));//方法引用list.forEach(System.out::println);1.2 接…...
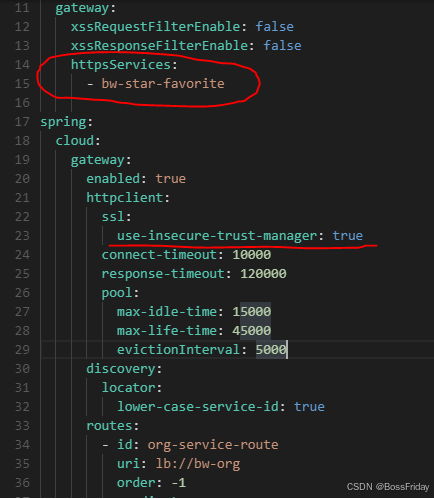
SpringCloud网关 SpringBoot服务 HTTP/HTTPS路由/监听双支持
背景 一般来说SpringCloud Gateway到后面服务的路由属于内网交互,因此路由方式是否是Https就显得不是那么重要了。事实上也确实如此,大多数的应用开发时基本都是直接Http就过去了,不会一开始就是直接上Https。然而随着时间的推移,…...

JavaScript做网页是否过期的处理
通过路由上的参数生成唯一md5和路由上token做验证_md5 token-CSDN博客 前言:基于这篇文章我们做网页是否超时,网页是否过期的处理。打开一个网页允许他在一定时间内可以访问,过了这个时间就不可以访问了,encrypt是h5加密方法&…...

python coding时遇到的问题
Q:只有cpu的时候加载模型 A:checkpoint torch.load(model_path, map_locationtorch.device(‘cpu’)) Q:vscode的文件路径和spyder的不一样 A:在vscode中,右键要用的文件,选择“文件相对路径”...

攻防演练号角吹响,聚铭铭察高级威胁检测系统助您零失分打赢重保攻坚战
在数字化浪潮中,攻防演练成为了衡量网络安全防御力的核心标尺,其重要性与日俱增。这项由政府、行业监管或企业内部主导的安全活动,随着互联网普及而兴起,现已发展成为全球公认的检验网络安全体系效能的标准。它不仅关乎技术实力的…...

个人量化交易兴起!有什么好用的量化软件推荐?迅投QMT量化平台简介!
QMT是专门为机构、活跃投资者、高净值客户等专业投资者研发的智能量化交易终端,拥有高速行情、极速交易、策略交易、多维度风控等专业功能,满足专业投资者的特殊交易需求。覆盖业务范围广:沪深A股、港股通、两融、期权、期货。 适合用QMT的投资者&#x…...

SQL labs-SQL注入(七,sqlmap对于post传参方式的注入,2)
本文仅作为学习参考使用,本文作者对任何使用本文进行渗透攻击破坏不负任何责任。参考:SQL注入之Header注入_sqlmap header注入-CSDN博客 序言: 本文主要讲解基于SQL labs靶场,sqlmap工具进行的post传参方式的SQL注入,…...

SAM 2: Segment Anything in Images and Videos
Introduction 提出的目的: 1.现有的应用像自动驾驶,AR等来说都是需要temporal localization beyond image-level segmentation(时序定位而不仅是图片分割) 2. 一个好的分割模型不应该仅仅局限于图片领域,而是图视频两…...

软件测试面试,如何自我介绍?
又是一年金九银十,相信不少小伙伴都在准备跳槽面试,而面试中一个必不可少的环节就是自我介绍,所以,今天我们就来聊一聊软件测试面试中如何自我介绍。 为什么要自我介绍 在讨论如何自我介绍之前,我们先来讨论一下为…...

力扣第四十七题——全排列II
内容介绍 给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。 示例 1: 输入:nums [1,1,2] 输出: [[1,1,2],[1,2,1],[2,1,1]]示例 2: 输入:nums [1,2,3] 输出:[[1,2,3],…...

Springer旗下中科院2区TOP,国人优势大!
关注GZH【欧亚科睿学术】,第一时间了解期刊最新动态! 1 通信网络类 【期刊简介】IF:4.0-5.0,JCR1区,中科院3区 【出版社】ELSEVIER出版社 【检索情况】SCIE&EI双检,CCF-C类 【征稿领域】通信网络的…...

【C++】C++入门知识详解(下)
大家好~我们接着【C】C入门知识详解(上)-CSDN博客来介绍另一些C入门基础知识。 1.缺省值和缺省参数 缺省参数就是声明或定义函数时为函数的参数指定一个缺省参数。在调用该函数时,如果没有指定实参,则采用该形参的缺省值…...
分压电阻方式的ADC电压校准
无人机有个流程是电池电压校准。具体做法是:让你用万用表测量一下电池两端的电压,然后输入到文本框中,电机计算能重新计算出电压分压器的值,从而获得电池电压值。 这种方法实现的原理是这样的: 电阻分压检测电压原理,以上图为例: 当电路确定时,R2/(R1+R2)是一个定值R,…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...

WebRTC调研
WebRTC是什么,为什么,如何使用 WebRTC有什么优势 WebRTC Architecture Amazon KVS WebRTC 其它厂商WebRTC 海康门禁WebRTC 海康门禁其他界面整理 威视通WebRTC 局域网 Google浏览器 Microsoft Edge 公网 RTSP RTMP NVR ONVIF SIP SRT WebRTC协…...

大数据治理的常见方式
大数据治理的常见方式 大数据治理是确保数据质量、安全性和可用性的系统性方法,以下是几种常见的治理方式: 1. 数据质量管理 核心方法: 数据校验:建立数据校验规则(格式、范围、一致性等)数据清洗&…...

解析“道作为序位生成器”的核心原理
解析“道作为序位生成器”的核心原理 以下完整展开道函数的零点调控机制,重点解析"道作为序位生成器"的核心原理与实现框架: 一、道函数的零点调控机制 1. 道作为序位生成器 道在认知坐标系$(x_{\text{物}}, y_{\text{意}}, z_{\text{文}}…...
