数据结构与算法 - 递归
一、递归
1. 概述
定义:在计算机科学中,递归是一种解决计算问题的方法,其中解决方案取决于同一类问题的更小子集。
比如单链表递归遍历的例子:
void f(Node node) {if(node == null) {return;}println("before:" + node.value)f(node.next);println("after:" + node.value)
}说明:
- 自己调用自己,如果说每个函数对应着一种解决方案,自己调用自己意味着解决方案是一样的(有规律的)
- 每次调用,函数处理的数据会较上次缩减(子集),而且最后会缩减至无需继续递归
- 内层函数调用(子集处理)完成,外层函数才能算调用完成
原理
假设链表中有3个节点,value分别为1,2,3,以上代码的执行流程类似于下面的伪码
// 1 -> 2 -> 3 -> null f(1)void f(Node node = 1) {println("before:" + node.value) // 1void f(Node node = 2) {println("before:" + node.value) // 2void f(Node node = 3) {println("before:" + node.value) // 3void f(Node node = null) {if(node == null) {return;}}println("after:" + node.value) // 3}println("after:" + node.value) // 2}println("after:" + node.value) // 1
}思路
1. 确定能否使用递归求解
2. 推导出递推关系,即父问题与子问题的关系,以及递归的结束条件
例如之前遍历链表的递推关系为

- 深入到最里层叫递
- 从最里层处理叫归
- 在递的过程中,外层函数内的局部变量(以及方法参数)并未消失,归的时候还可以用到
2. 单路递归Single Recursion
2.1 阶乘
用递归方法求阶乘
- 阶乘的定义:n! = 1 * 2 * 3 ... (n - 2) * (n - 1) * n,其中n为自然数,当然 0! = 1
- 递推关系

代码
private static int f(int n) {if (n == 1) {return 1;}return n * f(n - 1);
}拆解伪码如下,假设n初始值为3
f(int n = 3) { // 解决不了,递return 3 * f(int n = 2) { // 解决不了,继续递return 2 * f(int n = 1) {if (n == 1) { // 可以解决, 开始归return 1;}}}
}2.1 反向打印字符串
用递归反向打印字符串,n 为字符在整个字符串 str 中的索引位置
-
递:n 从 0 开始,每次 n + 1,一直递到 n == str.length() - 1
-
归:从 n == str.length() 开始归,从归打印,自然是逆序的
递推关系

代码为
public static void reversePrint(String str, int index) {if (index == str.length()) {return;}reversePrint(str, index + 1);System.out.println(str.charAt(index));
}2.2 二分查找(单路递归)
public static int binarySearch(int[] a, int target) {return recursion(a, target, 0, a.length - 1);
}public static int recursion(int[] a, int target, int i, int j) {if (i > j) {return -1;}int m = (i + j) >>> 1;if (target < a[m]) {return recursion(a, target, i, m - 1);} else if (a[m] < target) {return recursion(a, target, m + 1, j);} else {return m;}
}2.3 冒泡排序(单路递归)
- 将数组划分为两部分[0 ... j] [j + 1 ... a.length - 1]
- 左边[0 ... j]是未排序部分
- 右边[j + 1 ... a.length - 1]是已排序部分
- 未排序区间内,相邻的两个元素比较,如果前一个大于后一个,则交换位置
public static void main(String[] args) {int[] a = {3, 2, 6, 1, 5, 4, 7};bubble(a, 0, a.length - 1);System.out.println(Arrays.toString(a));
}private static void bubble(int[] a, int low, int high) {if(low == high) {return;}int j = low;for (int i = low; i < high; i++) {if (a[i] > a[i + 1]) {swap(a, i, i + 1);j = i;}}bubble(a, low, j);
}private static void swap(int[] a, int i, int j) {int t = a[i];a[i] = a[j];a[j] = t;
}- low与high为未排序范围
- j表示的是未排序的边界,下一次递归时的high
- 发生交换,意味着有无序情况
- 最后一次交换(以后没有无序)时,左侧i仍是无序,右侧i+1已然有序
private static void bubble(int[] a, int j) {if (j == 0) {return;}int x = 0; // x右侧的元素都是有序的for(int i = 0; i < j; i++) {{if(a[i] > a[i + 1]) {{int t = a[i];a[i] = a[i + 1];a[i + 1] = t;x = i;}}bubble(a, x);
}C++版冒泡排序:exchange右侧都是有序的
#include<iostream>
#include<vector>
using namespace std;void BubbleSort(vector<int>& data, int length){int j, exchange, bound, temp;exchange = length - 1; // 第一趟冒泡排序的区间是[0 ~ length - 1]while(exchange != 0){bound = exchange;exchange = 0;for(j = 0; j < bound; j++) // 一趟冒泡排序的区间是[0 ~ bound]{if(data[j] > data[j + 1]){temp = data[j];data[j] = data[j + 1];data[j + 1] = temp;exchange = j; // 记载每一次记录交换的位置 }} }
}2.4 插入排序(单路递归)
public static void main(String[] args) {int[] a = {3, 2, 6, 1, 5, 7, 4};insertion(a, 1, a.length - 1);System.out.println(Arrays.toString(a));
}private static void insertion(int[] a, int low, int high) {if (low > high) {return;}// low指针指的是未排序区的边界int i = low - 1; // 已排序区的指针int t = a[low];while (i >= 0 && a[i] > t) { // 没有找到插入位置a[i + 1] = a[i]; // 空出插入位置i--;}if(i + 1 != low) {a[i + 1] = t;} insertion(a, low + 1, high);
}public void insertionSort(int[] nums, int length) {int i, j, temp;for(i = 1; i < length; i++) {temp = nums[i];for(j = i - 1; j >= 0 && temp < nums[j]; j--) { // 寻找插入位置nums[j + 1] = nums[j]; // 后移}nums[j + 1] = temp;}
}2.5 约瑟夫问题(单路递归)
n个人排成圆圈,从头开始报数,每次数到第m个人杀之,继续从下一个人重复以上过程,求最后活下来的人是谁?
解法一:
设josephus(n, m)表示在n个人中,每m个人被杀时最后存活的人。递归关系为:
josephus(n, m) = (josephus(n - 1, m) + m) % n, n > 1
josephus(1, m) = 0
这个关系的意思是,若我们知道n-1个人时的存活者,我们可以通过调整索引来得出n个人时的存活者。

class Solution { public int findTheWinner(int n, int m) { return josephus(n, m) + 1; // 转换为1-based索引 } private int josephus(int n, int m) { if (n == 1) return 0; // 只有一个人时,返回其索引0 return (josephus(n - 1, m) + m) % n; // 递归公式 } public static void main(String[] args) { Solution solution = new Solution(); int n = 7; // 总人数 int m = 3; // 每次报数到m的人被杀 int winner = solution.findTheWinner(n, m); System.out.println("最后存活下来的人的位置是: " + winner); // 输出最后存活者的1-based索引 }
}3 多路递归 Multi Recursion
如果每个递归函数例包含多个自身调用,称之为multi recursion
3.1 裴波那契数列
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
示例 1:
输入:n = 2 输出:2 解释:有两种方法可以爬到楼顶。 1. 1 阶 + 1 阶 2. 2 阶
示例 2:
输入:n = 3 输出:3 解释:有三种方法可以爬到楼顶。 1. 1 阶 + 1 阶 + 1 阶 2. 1 阶 + 2 阶 3. 2 阶 + 1 阶
提示:
1 <= n <= 45
Java实现
解法一:递归,会超时
class Solution {public int climbStairs(int n) {if(n == 1) {return 1;}if(n == 2) {return 2;}return climbStairs(n - 1) + climbStairs(n - 2);}
}递归的次数也符合斐波那契数列规律:2 * f(n + 1) - 1
时间复杂度推导过程:

解法二:
class Solution {public int climbStairs(int n) {if(n == 1) {return 1;}if(n == 2) {return 2;}int prev = 1;int curr = 2;for(int i = 3; i <= n; i++) {int temp = curr;curr = prev + curr;prev = temp;}return curr;}
}3.2 兔子问题

第一个月,有一对未成熟的兔子。第二个月,它们成熟。第三个月,它们能产下一对新的小兔子。所有兔子遵循相同规律,求第n个月的兔子数量。
分析:设第n个月兔子数为f(n)
- f(n) = 上个月兔子数 + 新生的小兔子数
- 新生的小兔子数 = 上个月成熟的兔子数
- 因为需要一个月兔子就成熟,所以【上个月成熟的兔子数】也就是【上上个月的兔子数】
- 上个月兔子数,即f(n - 1);上上个月的兔子数,即f(n-2)
递推公式:f(n) = f(n -1) + f(n - 2)
class Solution {public int f(int n) {if(n == 1 || n == 2) {return 1;}int a = 1; // f(n-2)int b = 1; // f(n-1)int count = 0;for(int i = 3; i <= n; i++) {count = a + b;a = b; // 更新f(n-2)b = count; // 更新f(n-1)}return count;}
}3.3 汉诺塔问题(多路递归)
Tower of Hanoi,是一个源于印度古老传说:大梵天创建世界时做了三根金刚石柱,在一根柱子从下往上按大小顺序摞着 64 片黄金圆盘,大梵天命令婆罗门把圆盘重新摆放在另一根柱子上,并且规定
-
一次只能移动一个圆盘
-
小圆盘上不能放大圆盘
下面的动图演示了4片圆盘的移动方法

解法一:递归。时间复杂度:O(2^n)
递归分解:
- 若有n个盘子,以A、B和C分别表示起始柱、辅助柱和目标柱
- 首先,将前n-1个盘子从柱A移动到柱B,使用柱C作为辅助
- 接下来,将第n个盘子(最大的盘子)从柱A移动到柱C
- 最后,将n-1个盘子从柱B移动到柱C,使用柱A作为辅助
class Solution { public void hanota(List<Integer> A, List<Integer> B, List<Integer> C) { int n = A.size(); moveDisks(n, A, C, B); // A -> C, B为辅助 } private void moveDisks(int n, List<Integer> from, List<Integer> to, List<Integer> aux) { // 基本情况:如果没有盘子要移动,直接返回 if (n == 0) { return; } // 1. 将 n-1 个盘子从 "from" 移动到 "aux",使用 "to" 作为辅助 moveDisks(n - 1, from, aux, to); // 2. 将第 n 个盘子从 "from" 移动到 "to" to.add(from.remove(from.size() - 1)); // 从 "from" 中移除最后一个盘子并添加到 "to" // 3. 将 n-1 个盘子从 "aux" 移动到 "to",使用 "from" 作为辅助 moveDisks(n - 1, aux, to, from); }
} package com.itheima.algorithm.recursion_multi;import org.springframework.util.StopWatch;import java.util.LinkedList;/*** 递归汉诺塔*/
public class E02HanoiTower {static LinkedList<Integer> a = new LinkedList<>();static LinkedList<Integer> b = new LinkedList<>();static LinkedList<Integer> c = new LinkedList<>();static void init(int n) {for (int i = n; i >= 1; i--) {a.addLast(i);}}/*** <h3>移动圆盘</h3>** @param n 圆盘个数* @param a 由* @param b 借* @param c 至*/static void move(int n, LinkedList<Integer> a,LinkedList<Integer> b,LinkedList<Integer> c) {if (n == 0) {return;}move(n - 1, a, c, b); // 把 n-1 个盘子由a,借c,移至bc.addLast(a.removeLast()); // 把最后的盘子由 a 移至 c
// print();move(n - 1, b, a, c); // 把 n-1 个盘子由b,借a,移至c}// T(n) = 2T(n-1) + c, O(2^64)public static void main(String[] args) {StopWatch sw = new StopWatch();int n = 1;init(n);print();sw.start("n=1");move(n, a, b, c);sw.stop();print();System.out.println(sw.prettyPrint());}private static void print() {System.out.println("----------------");System.out.println(a);System.out.println(b);System.out.println(c);}
}
3.3 杨辉三角
给定一个非负整数 numRows,生成「杨辉三角」的前 numRows 行。
在「杨辉三角」中,每个数是它左上方和右上方的数的和。

示例 1:
输入: numRows = 5 输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]
示例 2:
输入: numRows = 1 输出: [[1]]
提示:
1 <= numRows <= 30
递推公式:triangle[i][j] = triangle[i - 1][j - 1] + triangle[i - 1][j]
解法一:迭代
class Solution { public List<List<Integer>> generate(int numRows) { List<List<Integer>> triangle = new ArrayList<>(); for (int i = 0; i < numRows; i++) { List<Integer> row = new ArrayList<>(i + 1); for (int j = 0; j <= i; j++) { if (j == 0 || j == i) { row.add(1); // 第一列和最后一列都为1 } else { // 当前元素等于上一行的两个元素之和 row.add(triangle.get(i - 1).get(j - 1) + triangle.get(i - 1).get(j)); } } triangle.add(row); // 将当前行添加到三角形中 } return triangle; }
}解法二:递归。这个递归方法对于较大的 numRows(接近 30)可能会非常低效,因为会有大量重复计算。对于较大的输入,推荐使用迭代的方法。
class Solution { public List<List<Integer>> generate(int numRows) { List<List<Integer>> triangle = new ArrayList<>(); for(int i = 0; i < numRows; i++) {triangle.add(generateRow(i));}return triangle; } private List<Integer> generateRow(int rowIndex) {List<Integer> row = new ArrayList<>();for(int j = 0; j <= rowIndex; j++) {row.add(getValue(rowIndex, j));}return row;}private int getValue(int row, int col) {if(col == 0 || col == row) {return 1;}return getValue(row - 1, col - 1) + getValue(row - 1, col);}
}解法二:递归优化。备忘录模式
二维数组记忆法
class Solution { public List<List<Integer>> generate(int numRows) { List<List<Integer>> triangle = new ArrayList<>(); // 创建一个二维数组用于存储已计算的值 Integer[][] memo = new Integer[numRows][numRows]; for (int i = 0; i < numRows; i++) { triangle.add(new ArrayList<>()); for (int j = 0; j <= i; j++) { triangle.get(i).add(getValue(i, j, memo)); } } return triangle; } private int getValue(int row, int col, Integer[][] memo) { // 如果位置超出边界,返回 0 if (col < 0 || col > row) { return 0; } // 如果是边界元素(最左或最右),返回 1 if (col == 0 || col == row) { return 1; } // 如果已经计算过,直接返回 if (memo[row][col] != null) { return memo[row][col]; } // 递归计算并存储结果到 memo memo[row][col] = getValue(row - 1, col - 1, memo) + getValue(row - 1, col, memo); return memo[row][col]; }
}解法三:一维数组记忆法。
private static void createRow(int[] row, int i) {if (i == 0) {row[0] = 1;return;}for (int j = i; j > 0; j--) {// 下一行当前项等于 上一行的当前项 + 前一项row[j] = row[j] + row[j - 1];}}public static void print2(int n) {int[] row = new int[n];for (int i = 0; i < n; i++) { // 行createRow(row, i);
// printSpace(n, i);for (int j = 0; j <= i; j++) {System.out.printf("%-4d", row[j]);}System.out.println();}}4. 递归优化 - 记忆法
斐波那契数列计算过程中存在很多重复的计算,例如求f(5)的递归分解过程

可以看到(颜色相同的是重复的)
- f(3)重复了2次
- f(2)重复了3次
- f(1)重复了5次
- f(0)重复了3次
随着n的增大,重复次数非常可观,如何优化呢?
Menoization记忆法(也称备忘录)是一种优化技术,通过存储函数调用结果(通常比较昂贵),当再次出现相同的输入(子问题)时,就能实现加速效果。
public static void main(String[] args) {int n = 13;int[] cache = new int[n + 1];Arrays.fill(cache, -1);cache[0] = 0;cache[1] = 1;System.out.println(f(cache, n));
}public static int f(int[] cache, int n) {if (cache[n] != -1) {return cache[n];}cache[n] = f(cache, n - 1) + f(cache, n - 2);return cache[n];
}优化后的图示,只要结果被缓存,就不会执行其子问题

- 改进前的时间复杂度为Θ(1.618^n);空间复杂度O(n)
- 改进后的时间复杂度为O(n);空间复杂度为O(n),额外的空间缓存结果
5. 递归优化 - 尾递归
用递归做 n + (n - 1) + (n - 2) + ... + 1
public static long sum(long n) {if(n == 1) {return 1;}return n + sum(n - 1);
}在我的机器上n = 12000时爆栈了
Exception in thread "main" java.lang.StackOverflowErrorat Test.sum(Test.java:10)at Test.sum(Test.java:10)at Test.sum(Test.java:10)at Test.sum(Test.java:10)at Test.sum(Test.java:10)...为什么呢?
- 每次方法调用都是需要消耗一定的栈内存的,这些内存用来存储方法参数、方法内局部变量、返回地址等。
- 方法调用占用的内存需要等待方法结束时才会释放
- 而递归调用不到最深不会回头,最内层方法没完成之前,外层方法都结束不了。
尾调用
如果函数的最后一步是调用一个函数,那么称为尾调用,例如
function a() {return b()
}下面三段代码不能叫作尾调用
function a() {const c = b()return c
}- 最后一步并非调用函数
function a() {return b() + 1
}- 最后一步执行的是加法
function a(x) {return b() + x
}- 最后一步执行的是加法
一些语言的编译器能够对尾调用做优化,例如
function a() {// 做前面的事return b()
}function b() {// 做前面的事return c()
}function c() {return 1000
}a()没优化之前的伪码
function a() {return function b() {return function c() {return 1000}}
}优化后的伪码如下
a()
b()
c()为何尾递归才能优化?
调用a时
- a返回时发现,没什么可留给b的,将来返回的结果b提供就可以了,用不着我a了,我的内存就可以释放
调用b时
- b返回时发现,没什么可以留给c的,将来返回的结果c提供就可以了,用不着我b了,我的内存就可以释放了
如果调用a时
- 不是尾调用,例如return b() + 1,那么a就不能提前结束,因为它还得利用b的结果做加法
尾递归:是尾调用的一种特例,也就是最后一步执行的是同一个函数
尾递归避免爆栈
安装Scala

Scala入门
object Main {def main(args: Array[String]): Unit = {println("Hello Scala")}
}- Scala是Java的近亲,Java中的类都可以拿来重用
- 类型是放在变量后面的
- Unit表示无返回值,类似于void
- 不需要以分号作为结尾,当然加上也对
先写一个会爆栈的函数
def sum(n: Long): Long = {if (n == 1) {return 1}return n + sum(n - 1)
}Scala最后一行代码若作为返回值,可以省略return
在n = 11000时出了异常
println(sum(11000))Exception in thread "main" java.lang.StackOverflowErrorat Main$.sum(Main.scala:25)at Main$.sum(Main.scala:25)at Main$.sum(Main.scala:25)at Main$.sum(Main.scala:25)...这时因为以上代码,这不是尾调用,要想成为尾调用,那么:
最后一行代码,必须是一次函数调用
内层函数必须摆脱与外层函数的关系,内层函数执行后不依赖于外层的变量或常量
def sum(n: Long): Long = {if (n == 1) {return 1}return n + sum(n - 1) // 依赖于外层函数的 n 变量
}如何让它执行后就拜托对n的依赖呢?
- 不能等递归回来再做加法,那样就必须保留外层的n
- 把n当作内层函数的一个参数传进去,这时n就属于内层函数了
- 传参时就完成累加,不必等回来时累加
sum(n - 1, n + 累加器)改写后代码如下
@tailrec
def sum(n: Long, accumulator: Long): Long = {if (n == 1) {return 1 + accumulator} return sum(n - 1, n + accumulator)
}accumulator作为累加器
@tailrec注解是scala提供的,用来检查方法是否符合尾递归
这回sum(10000000, 0)也没有问题,打印50000005000000
执行流程如下,以伪码表示sum(4, 0)
// 首次调用
def sum(n = 4, accumulator = 0): Long = {return sum(4 - 1, 4 + accumulator)
}// 接下来调用内层 sum, 传参时就完成了累加, 不必等回来时累加,当内层 sum 调用后,外层 sum 空间没必要保留
def sum(n = 3, accumulator = 4): Long = {return sum(3 - 1, 3 + accumulator)
}// 继续调用内层 sum
def sum(n = 2, accumulator = 7): Long = {return sum(2 - 1, 2 + accumulator)
}// 继续调用内层 sum, 这是最后的 sum 调用完就返回最后结果 10, 前面所有其它 sum 的空间早已释放
def sum(n = 1, accumulator = 9): Long = {if (1 == 1) {return 1 + accumulator}
}本质上,尾递归优化就是将函数的递归调用,变成了函数的循环调用
改循环避免爆栈
public static void main(String[] args) {long n = 100000000;long sum = 0;for (long i = n; i >= 1; i--) {sum += i;}System.out.println(sum);
}6. 递归时间复杂度 - 主定理(Master theorem)
若有递归式

其中
- T(n)是问题的运行时间,n是数据规模
- a是子问题的个数
- T(n/b)是子问题运行时间,每个子问题被拆成原问题数据规模的n/b
- f(n)是除递归外执行的计算
令x = log_b a,即x = log_子问题缩小倍数 子问题个数,那么

例1:T(n) = 2T(n/2) + n ^ 4
- 此时x = 1 < 4,由后者决定整个时间复杂度Θ(n^4)
例2:T(n) = T(7n / 10) + n
- 此时x = 0 < 1,由后者决定整个时间复杂度Θ(n)
例3:T(n) = 16T(n/4) + n^2
- a = 16, b = 4, x = 2, x = 2;此时x = c = 2,时间复杂度为Θ(n^2 * logn)
例4:T(n) = 7T(n/3) + n^2
- a = 7, b = 3, c = 2, x = 1.?;此时x < c,由后者决定整个时间复杂度Θ(n^2)
例5:T(n) = 7T(n/2) + n^2
- a = 7, b = 2, c = 2, x = 2.? > c,由前者决定整个时间复杂度Θ(n^log_2 7)
例6:T(n) = 2T(n/4) + sqrt(n)
- a = 2, b = 4, c = 1/2,x = c,时间复杂度为Θ(sqrt(n) * logn)
例7:二分查找递归
int f(int[] a, int target, int i, int j) {if (i > j) {return -1;}int m = (i + j) >>> 1;if (target < a[m]) {return f(a, target, i, m - 1);} else if (a[m] < target) {return f(a, target, m + 1, j);} else {return m;}
}- 子问题个数a = 1
- 子问题数据规模缩小倍数b = 2
- 除递归之外执行的计算是常数级c = 0
- 此时x = 0 = c,时间复杂度为Θ(logn)
例8:归并排序递归
void split(B[], i, j, A[])
{if (j - i <= 1) return; m = (i + j) / 2; // 递归split(A, i, m, B); split(A, m, j, B); // 合并merge(B, i, m, j, A);
}- 子问题个数a = 2
- 子问题数据规模缩小倍数b = 2
- 除递归外,主要时间花在合并上,它可以用f(n) = n表示
- T(n) = 2T(n/2) + n,此时x = 1 = c,时间复杂度Θ(nlogn)
例9:快速排序递归
algorithm quicksort(A, lo, hi) is if lo >= hi || lo < 0 then return// 分区p := partition(A, lo, hi) // 递归quicksort(A, lo, p - 1) quicksort(A, p + 1, hi) -
子问题个数 a=2
-
子问题数据规模缩小倍数
-
如果分区分的好,b=2
-
如果分区没分好,例如分区1 的数据是 0,分区 2 的数据是 n-1
-
-
除递归外,主要时间花在分区上,它可以用 $f(n) = n 表示
情况1 - 分区分的好
T(n) = 2T(n\2) + n
-
此时 x=1=c,时间复杂度 Θ(nlogn)
情况2 - 分区没分好
T(n) = T(n-1) + T(1) + n
-
此时不能用主定理求解
7. 递归时间复杂度 - 展开求解
像下面的递归式,都不能用主定理求解
例1:递归求和
long sum(long n) {if (n == 1) {return 1;}return n + sum(n - 1);
}T(n) = T(n - 1) + c,T(1) = c
下面为展开过程
T(n) = T(n-2) + c + c
T(n) = T(n-3) + c + c + c
...
T(n) = T(n-(n-1)) + (n-1)c
-
其中 T(n-(n-1)) 即 T(1)
-
带入求得 T(n) = c + (n-1)c = nc
时间复杂度为 O(n)
例2:递归冒泡排序
void bubble(int[] a, int high) {if(0 == high) {return;}for (int i = 0; i < high; i++) {if (a[i] > a[i + 1]) {swap(a, i, i + 1);}}bubble(a, high - 1);
}T(n) =T(n - 1) + n,T(1) = c
下面为展开过程
T(n) = T(n-2) + (n-1) + n
T(n) = T(n-3) + (n-2) + (n-1) + n
...
T(n) = T(1) + 2 + ... + n = T(1) + (n-1)*(2+n)/2 = c + n^2/2 + n/2 -1
时间复杂度 O(n^2)
注:等差数列求和为 个数 * (首项 + 末项)/2
例3:递归快排
快速排序分区没分好的极端情况
T(n) = T(n-1) + T(1) + n,T(1) = c
T(n) = T(n-1) + c + n
下面为展开过程
T(n) = T(n-2) + c + (n-1) + c + n
T(n) = T(n-3) + c + (n-2) + c + (n-1) + c + n
...
T(n) = T(n-(n-1)) + (n-1)c + 2+...+n = n^2 / 2 + (2cn + n) / 2 -1
时间复杂度 O(n^2)
不会推导的同学可以进入 Wolfram|Alpha: Computational Intelligence
-
例1 输入 f(n) = f(n - 1) + c, f(1) = c
-
例2 输入 f(n) = f(n - 1) + n, f(1) = c
-
例3 输入 f(n) = f(n - 1) + n + c, f(1) = c
相关文章:

数据结构与算法 - 递归
一、递归 1. 概述 定义:在计算机科学中,递归是一种解决计算问题的方法,其中解决方案取决于同一类问题的更小子集。 比如单链表递归遍历的例子: void f(Node node) {if(node null) {return;}println("before:" node…...

python:plotly 网页交互式数据可视化工具
pip install plotly plotly-5.22.0-py3-none-any.whl pip install plotly_express 包含:GDP数据、餐厅的订单流水数据、鸢尾花 Iris数据集 等等 pip show plotly Name: plotly Version: 5.22.0 Summary: An open-source, interactive data visualization librar…...

聊一聊 webpack5性能优化有哪些?
介绍 此文章基于webpack5来阐述 webpack性能优化较多,可以对其进行分类 优化打包速度,开发或者构建时优化打包速度(比如exclude、catch等)优化打包后的结果,上线时的优化(比如分包处理、减小包体积、CDN…...

公布一批神马爬虫IP地址,真实采集数据
一、数据来源: 1、这批神马爬虫IP来源于尚贤达猎头公司网站采集数据; 2、数据采集时间段:2023年10月-2024年1月; 3、判断标准:主要根据用户代理是否包含“YisouSpider”,具体IP没做核实。 二、神马爬虫主…...

uni-app全局文件与常用API
文章目录 rpx响应式单位import导入css样式及scss变量用法与static目录import导入css样式uni.scss变量用法 pages.json页面路由globalStyle的属性pages设置页面路径及窗口表现tabBar设置底部菜单选项及iconfont图标 vite.config中安装插件unplugin-auto-import自动导入vue和unia…...
连接器表面缺陷检测方案
连接器是一种用于连接电子设备或电路中不同部件之间的组件,通常用于传输电力、信号或数据。连接器的设计和类型各不相同,以适应不同设备和应用的需求。连接器用于连接电子设备之间的电线、电缆或电路板,实现信号传输和电力供应。连接器设计应…...

React项目动态设置index.html中的<title>标签内容
1. 安装react-helmet-async npm install react-helmet-async -S2. 如下修改App.tsx即可 import { ConfigProvider } from "antd"; import { RouterProvider } from "react-router-dom"; import { router } from "//router"; import { Helmet, …...

大龄程序员转型攻略:拥抱人工智能,开启新征程
前言 随着科技的飞速发展,人工智能浪潮席卷全球,相关岗位炙手可热。在这个背景下,许多大龄程序员开始思考如何转型,以适应时代的变化。结合自身编程基础,大龄程序员可以学习机器学习、深度学习算法,投身于…...

Jenkins保姆笔记(1)——基于Java8的Jenkins安装部署
前言 记录分享下Jenkins的相关干货知识。分2-3篇来介绍Jenkins的安装部署以及使用。还是和以前一样,文章不介绍较多概念和细节,多介绍实践过程,以战代练,来供大家学习和理解Jenkins 概念 Jenkins是一个开源的自动化服务器&…...
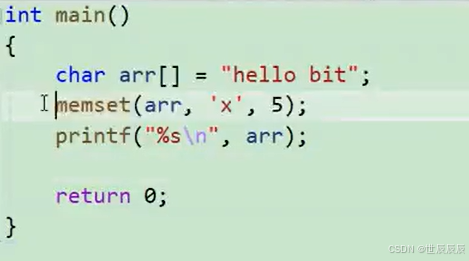
学习c语言第18天(字符串和内存函数)
1.函数介绍 1.1 strlen size_t(就是无符号整形) strlen(const char * str); 字符串已经\0作为结束标志,strlen函数返回的是在字符串中\0前面出现的字符个数(不包 含\0) 参数指向的字符串必须要以\0结束。 注意函数的返回值为size_t,…...

无心剑七绝《潘展乐神》
七绝潘展乐神 潘江陆海忘情游 展志凌云筑玉楼 乐创全球新纪录 神姿英发舞金钩 2024年8月1日 平水韵十一尤平韵 潘展乐神,这四个字,如同四座矗立的丰碑,分别代表了潘展乐在游泳领域的卓越成就、豪情壮志、快乐创新和非凡风采。无心剑的这首…...

Linux C++ 开发1 - 搭建C++开发环境
1. 安装GCC/GDB 1.1. 安装1.2. 校验 2. 安装CMake 2.1. 安装2.2. 校验 3. 安装IDE 3.1. VSCode3.2. CLion 1. 安装GCC/GDB 1.1. 安装 # 更新软件源 sudo apt update # 通过以下命令安装编译器和调试器 sudo apt install build-essential gdb Ubuntu 默认情况下没有提供C/C…...

吴恩达老师机器学习-ex4
梯度检测没有实现。有借鉴网上的部分 导入相关库,读取数据 因为这次的数据是mat文件,需要使用scipy库中的loadmat进行读取数据。 通过对数据类型的分析,发现是字典类型,查看该字典的键,可以发现又X,y等关…...

C语言-函数例题
函数经典例题 1、编写一个函数实现该功能:从键盘输入一个字串符, 再输入两个正整数 m 和 n, 输出字符串中从 m 开始, 连续 n 个字符。例如, 输入 abcdefg,2,3,输出 bcd. #include <stdio.h> /*作者: zcy日期:功能描述:编写…...

鸿蒙应用框架开发【多HAP】程序框架
多HAP 介绍 本示例展示多HAP开发,简单介绍了多HAP的使用场景,应用包含了一个entry HAP和两个feature HAP,两个feature HAP分别提供了音频和视频播放组件,entry中使用了音频和视频播放组件。 三个模块需要安装三个hap包ÿ…...

PG如何实现跨大版本升级
数据库进行升级,是一个再正常不过的功能,比如功能的需要,遇到BUG,安全漏洞等等,具体升级包含子版本升级,主版本升级。如果用过ORACLE的朋友,一定知道,在ORACLE中,如果要实…...

JDK 8 升级 17 及 springboot 2.x 升级 3.x 指南
JDK 8 升级 17 简介 从 JDK 8 升级到 JDK 17 的过程中,有几个主要的变化,特别是 Java Platform Module System (JPMS) 的引入,以及一些包路径的调整。以下是与 JDK 17 相关的一些重要变化: Java Platform Module System (JPMS) …...

基于java的人居环境整治管理系统(源码+lw+部署文档+讲解等)
前言 💗博主介绍:✌全网粉丝20W,CSDN特邀作者、博客专家、CSDN新星计划导师、全栈领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java、小程序技术领域和毕业项目实战✌💗 👇🏻…...

深入了解Pip:Python包管理器的详细指南
目录 Pip简介Pip的安装与升级Pip的基本使用 安装包卸载包列出已安装的包查看包的信息 管理依赖 使用requirements.txt冻结当前环境的包 Pip进阶用法 安装特定版本的包使用代理安装包从本地文件安装包 创建和发布Python包 创建一个Python包编写setup.py文件发布到PyPI 常见问题…...

Corsearch 用 ClickHouse 替换 MySQL 进行内容和品牌保护
本文字数:3357;估计阅读时间:9 分钟 作者:ClickHouse Team 本文在公众号【ClickHouseInc】首发 Chase Richards 自 2011 年在初创公司 Marketly 担任工程负责人,直到 2020 年公司被收购。他现在是品牌保护公司 Corsear…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...
