成为git砖家(10): 根据文件内容生成SHA-1
文章目录
- 1. `.git/objects` 目录
- 2. `git cat-file` 命令
- 3. 根据文件内容生成 sha-1
- 4. 结语
- 5. References
1. .git/objects 目录
git 是一个根据文件内容进行检索的系统。 当创建 hello.py, 填入
print("hello, world")
的内容, 并执行
git add hello.py
git commit -m "init"
会在 .git/objects 目录生成子目录和文件。 子目录是2位,文件则是38位, 子目录和文件名字拼接起来的到的40位哈希码, 就是 SHA-1:

比较新版本的 git, 当执行上述 git 操作后, 会在 .git/objects 里存储多个子目录, 旧版本的 git 则只生成一个子目录。我用的 git 2.45.2, 目录结构为:

2. git cat-file 命令
git cat-file 命令能查看 sha-1 的情况, 这里暂时未查阅文档, 仅做基本介绍。
git cat-file -t <sha-1> 查看的是 sha-1 的类型。 其中 sha-1 是子目录和文件拼接起来的。例如
➜ test git:(main) ✗ git cat-file -t 8cde7829c178ede96040e03f17c416d15bdacd01
blob
git cat-file -p <sha-1> 则是查看 blob 类型的内容:
➜ test git:(main) ✗ git cat-file -p 8cde7829c178ede96040e03f17c416d15bdacd01
print("hello world")
3. 根据文件内容生成 sha-1
git 其实已经帮我们计算了 sha-1, 这是它存储文件时最基本的计算。 当我们有两个内容完全一样的文件被 git add 和 git commit, 对应的 blob 对象是相同的。
作为验证,我们拷贝 hello.py 内容并提交:
➜ test git:(main) ✗ cp hello.py world.py
➜ test git:(main) ✗ git add world.py
➜ test git:(main) ✗ git commit -m "add world.py"
[main f72f05d] add world.py1 file changed, 1 insertion(+)create mode 100644 world.py

发现 .git/objects 目录新增的两个子目录,分别是 tree 和 commit 类型,并不是 blob 类型。 换言之, world.py 和 hello.py 对应的 blob 都是 8cde7829c17.
作为验证, 可以使用 Python 的 hashlib模块, 基于如下格式算出 sha-1:
blob {文件内容长度}\0 {file_content}
其中 {file_content} 是文件内容.
的到的结果是:
➜ test git:(main) ✗ python githash.py hello.py
8cde7829c178ede96040e03f17c416d15bdacd01
➜ test git:(main) ✗ python githash.py world.py
8cde7829c178ede96040e03f17c416d15bdacd01
具体的 githash.py 实现如下:
#!/usr/bin/env python3from sys import argv
from hashlib import sha1
from io import StringIOclass Githash(object):def __init__(self):self.buf = StringIO()def update(self, data):self.buf.write(data)def hexdigest(self):data = self.buf.getvalue().encode('utf-8')h = sha1()h.update(f"blob {len(data)}\0".encode('utf-8'))h.update(data)return h.hexdigest()def githash_data(data):h = Githash()h.update(data)return h.hexdigest()def githash_fileobj(fileobj):return githash_data(fileobj.read())if __name__ == '__main__':for filename in argv[1:]:with open(filename, 'r', encoding='utf-8') as fileobj:print(githash_fileobj(fileobj))
4. 结语
.git/objects 目录存放的子目录中, 有些子目录是 blob 类型的对象, 表示了文件内容。 当两个文件内容一致时, git 对它们生成相同的 SHA-1。 在了解 blob 类型对象的 sha-1 计算过程的前提下,基于 Python 的 hashlib 写了一个工具, 能根据文件内容算出 sha-1, 这既可以作为理解 git 对象存储的初步, 也可以作为后续自行实现一个 mini-git 的基础。
5. References
- https://gist.github.com/msabramo/763200
- https://www.bilibili.com/video/BV1FZ4y1W7ZS/?p=2&spm_id_from=pageDriver
相关文章:

成为git砖家(10): 根据文件内容生成SHA-1
文章目录 1. .git/objects 目录2. git cat-file 命令3. 根据文件内容生成 sha-14. 结语5. References 1. .git/objects 目录 git 是一个根据文件内容进行检索的系统。 当创建 hello.py, 填入 print("hello, world")的内容, 并执行 git add hello.py gi…...

园区导航小程序:一站式解决园区导航问题,释放存储,优化访客体验
随着园区的规模不断扩大,功能区划分日益复杂,导致访客和新员工在没有有效导航的情况下容易迷路。传统APP导航虽能解决部分问题,但其下载安装繁琐、占用手机内存大、且非高频使用导致的闲置,让许多用户望而却步。园区导航小程序的出…...
)
对于n进制转十进制的解法及代码(干货!)
对于p进制转十进制,我们有:(x)pa[0]*p^0a[1]*p^1a[2]*p^2...a[n]*p^n 举个例子:(11001)21*10*20*41*81*1625 (9FA)1610*16^015*16^19*16^22554 据此,我们可以编出c代码来解决问题 …...

当代互联网打工人的生存现状,看完泪流满面!
欢迎私信小编,了解更多产品信息呦~...

花几千上万学习Java,真没必要!(三十八)
测试代码1: package iotest.com; import java.nio.charset.StandardCharsets; import java.io.UnsupportedEncodingException; public class StringByteConversion { public static void main(String[] args) throws UnsupportedEncodingException { // 原始字…...

Zilliz 2025届校园招聘正式启动,寻找向量数据库内核开发工程师
为了解决非结构化数据处理问题,我们构建了向量数据库-Milvus! Milvus 数据库不仅是顶级开源基金会 LF AI&Data 的毕业项目,还曾登上数据库顶会SIGMOD、VLDB,在全球首届向量检索比赛中夺冠。目前,Milvus 项目已获得超过 2.8w s…...

TwinCAT3 新建项目教程
文章目录 打开TwinCAT 新建项目(通过TcXaeShell) 新建项目(通过VS 2019)...

大模型算法面试题(十九)
本系列收纳各种大模型面试题及答案。 1、SFT(有监督微调)、RM(奖励模型)、PPO(强化学习)的数据集格式? SFT(有监督微调)、RM(奖励模型)、PPO&…...

应用地址信息获取新技巧:Xinstall来助力
在移动互联网时代,应用获取用户地址信息的需求越来越普遍。无论是为了提供个性化服务,还是进行精准营销,地址信息都扮演着至关重要的角色。然而,如何合规、准确地获取这一信息,却是许多开发者面临的挑战。今天…...

图的最短路径算法:Dijkstra、Floyd-Warshall、Bellman-Ford
本文意在探讨图中最短路径算法 Dijkstra、Floyd-Warshall、Bellman-Ford 的对比和细节 整体分为如下四部分 总结性的比较了 Dijkstra、Floyd-Warshall、Bellman-FordDijkstra 算法介绍Floyd-Warshall 算法介绍Bellman-Ford 算法介绍 其中1、2、3 算法介绍部分会比较简洁&…...
)
Camera的pipline(TODO)
(TODO)...

非关系数据库-非关系数据库入门指南
非关系数据库入门指南 1. 引言:非关系数据库的兴起 在互联网技术飞速发展的今天,传统的关系型数据库面对海量数据和高并发访问时逐渐显得力不从心。于是,非关系数据库(NoSQL,Not Only SQL)应运而生&…...
)
看门狗IWDG、WWDG(速记版)
内置的看门狗有 独立看门狗 IWDG 和 窗口看门狗 WWDG 都用来在程序卡死的时候复位程序。 独立看门狗只有一个最晚时间界限。窗口看门狗有一个最早界限和最晚界限。独立看门狗有独立的时钟,一般设置来源时钟LSI40KHz。窗口看门狗挂靠在APB1总线上36MHz。 IWDG IWDG处于VDD供…...

ETL工程师角度下的SQL优化
作为ETL(Extract, Transform, Load)工程师,SQL优化是提高数据处理和分析效率的关键一环。优化SQL查询可以显著降低数据处理时间,提高ETL过程的性能。本文将从 合理设计数据模型:在ETL过程中,正确的数据模型…...
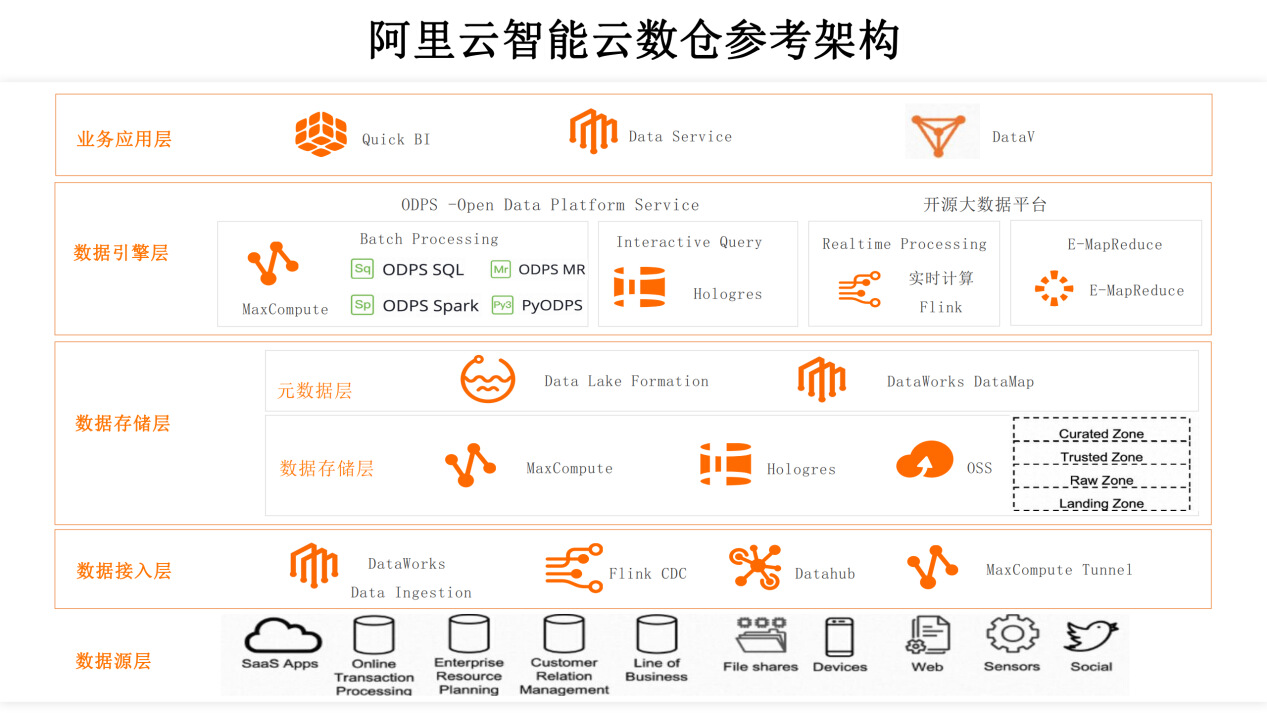
阿里云实时计算Flink在多行业的应用和实践
摘要:本文整理自 Flink Forward Asia 2023 中闭门会的分享。主要分享实时计算在各行业的应用实践,对回归实时计算的重点场景进行介绍以及企业如何使用实时计算技术,并且提供一些在技术架构上的参考建议。内容分为以下四个部分: 业…...
)
开源项目与工具:C++中的高性能并发库 - Intel Threading Building Blocks (TBB)
在C++的世界里,随着多核处理器成为常态,如何有效利用这些多核资源以实现高性能的并发编程成为了开发者们关注的焦点。Intel Threading Building Blocks (TBB) 作为一个专为并行编程设计的C++库,凭借其易用性、高效性和可扩展性,在高性能计算、游戏开发、金融分析等多个领域…...

Chapter 22 数据可视化——折线图
欢迎大家订阅【Python从入门到精通】专栏,一起探索Python的无限可能! 文章目录 前言一、Pyecharts介绍二、安装Pyecharts三、全局配置项四、绘制折线图 前言 在大数据时代,数据可视化成为了分析和展示数据的重要手段。Pyecharts 是一个基于 …...

管理流创建schema流程源码解析
一、简析 schema是pulsar重要的功能之一,现在就一起从源码的视角看下管理流创建schema时客户端和服务端的表现 客户端 客户端主要经历以下四个步骤 创建Schema实例 根据数据类型创建相对应的实例,例如Avro创建AvroSchema、JSON创建JSONSchema等 获取…...

【iOS】iOS内存五大分区
iOS内存五大分区 总揽 iOS中,内存主要分为五大区域:栈区,堆区,全局区/静态区,常量区和代码区。总览图如下。 这个图我觉得更好记,因为下面是低地址,上面是高地址,是比较符合日常…...

【项目实战】—— 高并发内存池
文章目录 什么是高并发内存池?项目介绍一、项目背景二、项目目标三、核心组件四、关键技术五、应用场景六、项目优势 什么是高并发内存池? 高并发内存池是一种专门设计用于高并发环境下的内存管理机制。它的原型是Google的一个开源项目tcmallocÿ…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

go 里面的指针
指针 在 Go 中,指针(pointer)是一个变量的内存地址,就像 C 语言那样: a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10,通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...
