B树的平衡性与性能优化
B树的平衡性与性能优化
B树(B-tree)是一种自平衡的树数据结构,广泛应用于数据库和文件系统中,用于保持数据的有序性并允许高效的插入、删除和查找操作。B树能够很好地处理大规模数据,并在磁盘I/O操作中表现出色。本文将详细探讨B树的平衡性和性能优化策略,深入源码进行解析,全面了解其内部机制和优化方法。
目录
- B树概述
- B树的结构和性质
- B树的平衡性
- 自动平衡机制
- 插入操作中的平衡性维护
- 删除操作中的平衡性维护
- B树的性能优化
- 高效的磁盘I/O操作
- 内存优化
- 并行化与并发控制
- B树的应用场景与案例分析
- 源码解析
- B树的基本操作源码分析
- 平衡性维护源码解析
- 性能优化源码解析
- 总结
1. B树概述
B树是一种广义的平衡多叉树,它能够在保持数据有序的同时,实现快速的查找、插入和删除操作。B树的设计目标是减少磁盘I/O操作,使其非常适合于存储系统和数据库系统。B树的每个节点可以包含多个子节点,这样可以更有效地利用磁盘块,并减少树的高度。
2. B树的结构和性质
结构
B树由根节点、内部节点和叶子节点组成。每个节点包含若干键值和子节点指针。B树的节点结构如下:
class BTreeNode {
public:int *keys; // 存储键值的数组int t; // 最小度数BTreeNode **C; // 存储子节点指针的数组int n; // 当前存储的键值数量bool leaf; // 是否为叶子节点BTreeNode(int _t, bool _leaf); // 构造函数// 插入一个新的键值到非满节点void insertNonFull(int k);// 分裂子节点void splitChild(int i, BTreeNode *y);// 其他操作,如删除、查找等
};
性质
- 节点的键值数量:每个节点至少包含
t-1个键值,最多包含2t-1个键值。 - 根节点的特殊性:根节点至少包含一个键值。
- 平衡性:所有叶子节点都位于同一层,树的高度平衡。
- 子节点数量:非叶子节点的子节点数量为键值数量加一。
3. B树的平衡性
自动平衡机制
B树的平衡性通过其插入和删除操作自动维护。在插入和删除过程中,通过节点的分裂和合并操作来保持树的平衡。具体来说:
- 插入操作:当一个节点满时,进行分裂操作,将中间键提升到父节点,从而保持树的平衡。
- 删除操作:当删除导致某个节点的键值数量少于
t-1时,通过节点合并和键值借用来保持平衡。
插入操作中的平衡性维护
插入操作时,如果目标节点已满,需要进行分裂操作:
- 找到插入位置。
- 如果节点满,则分裂节点,将中间键提升到父节点。
- 递归调整父节点,直至根节点。
插入操作的代码示例:
void BTreeNode::insertNonFull(int k) {int i = n-1;if (leaf) {// 在叶子节点中插入新的键值while (i >= 0 && keys[i] > k) {keys[i+1] = keys[i];i--;}keys[i+1] = k;n = n+1;} else {// 找到子节点进行递归插入while (i >= 0 && keys[i] > k)i--;if (C[i+1]->n == 2*t-1) {// 子节点满,进行分裂splitChild(i+1, C[i+1]);if (keys[i+1] < k)i++;}C[i+1]->insertNonFull(k);}
}void BTreeNode::splitChild(int i, BTreeNode *y) {BTreeNode *z = new BTreeNode(y->t, y->leaf);z->n = t - 1;for (int j = 0; j < t-1; j++)z->keys[j] = y->keys[j+t];if (!y->leaf) {for (int j = 0; j < t; j++)z->C[j] = y->C[j+t];}y->n = t - 1;for (int j = n; j >= i+1; j--)C[j+1] = C[j];C[i+1] = z;for (int j = n-1; j >= i; j--)keys[j+1] = keys[j];keys[i] = y->keys[t-1];n = n + 1;
}
删除操作中的平衡性维护
删除操作较为复杂,需要考虑以下几种情况:
- 删除叶子节点中的键值:直接删除,并调整节点中的键值。
- 删除内部节点中的键值:用前驱或后继键值替代,并递归删除。
- 借用兄弟节点的键值:如果兄弟节点有多余的键值,可以借用来保持平衡。
- 节点合并:如果兄弟节点没有多余键值,需要进行节点合并。
删除操作的代码示例:
void BTreeNode::remove(int k) {int idx = findKey(k);if (idx < n && keys[idx] == k) {if (leaf)removeFromLeaf(idx);elseremoveFromNonLeaf(idx);} else {if (leaf) {cout << "The key " << k << " does not exist in the tree\n";return;}bool flag = (idx == n);if (C[idx]->n < t)fill(idx);if (flag && idx > n)C[idx-1]->remove(k);elseC[idx]->remove(k);}
}void BTreeNode::removeFromLeaf(int idx) {for (int i = idx+1; i < n; ++i)keys[i-1] = keys[i];n--;
}void BTreeNode::removeFromNonLeaf(int idx) {int k = keys[idx];if (C[idx]->n >= t) {int pred = getPred(idx);keys[idx] = pred;C[idx]->remove(pred);} else if (C[idx+1]->n >= t) {int succ = getSucc(idx);keys[idx] = succ;C[idx+1]->remove(succ);} else {merge(idx);C[idx]->remove(k);}
}int BTreeNode::getPred(int idx) {BTreeNode *cur = C[idx];while (!cur->leaf)cur = cur->C[cur->n];return cur->keys[cur->n-1];
}int BTreeNode::getSucc(int idx) {BTreeNode *cur = C[idx+1];while (!cur->leaf)cur = cur->C[0];return cur->keys[0];
}void BTreeNode::fill(int idx) {if (idx != 0 && C[idx-1]->n >= t)borrowFromPrev(idx);else if (idx != n && C[idx+1]->n >= t)borrowFromNext(idx);else {if (idx != n)merge(idx);elsemerge(idx-1);}
}void BTreeNode::borrowFromPrev(int idx) {BTreeNode *child = C[idx];BTreeNode *sibling = C[idx-1];for (int i = child->n-1; i >= 0; --i)child->keys[i+1] = child->keys[i];if (!child->leaf) {for (int i = child->n; i >= 0; --i)child->C[i+1] = child->C[i];}child->keys[0] = keys[idx-1];if (!child->leaf)child->C[0] = sibling->C[sibling->n];keys[idx-1] = sibling->keys[sibling->n-1];child->n += 1;sibling->n -= 1;
}void BTreeNode::borrowFromNext(int idx) {BTreeNode *child = C[idx];BTreeNode *sibling = C[idx+1];child->keys[child->n] = keys[idx];if (!child->leaf)child->C[child->n+1] = sibling->C[0];keys[idx] = sibling->keys[0];for (int i = 1; i < sibling->n; ++i)sibling->keys[i-1] = sibling->keys[i];if (!sibling->leaf) {for (int i = 1; i <= sibling->n; ++i)sibling->C[i-1] = sibling->C[i];}child->n += 1;sibling->n -= 1;
}void BTreeNode::merge(int idx) {BTreeNode *child = C[idx];BTreeNode *sibling = C[idx+1];child->keys[t-1] = keys[idx];for (int i = 0; i < sibling->n; ++i)child->keys[i+t] = sibling->keys[i];if (!child->leaf) {for (int i = 0; i <= sibling->n; ++i)child->C[i+t] = sibling->C[i];}for (int i = idx+1; i < n; ++i)keys[i-1] = keys[i];for (int i = idx+2; i <= n; ++i)C[i-1] = C[i];child->n += sibling->n + 1;n--;delete sibling;
}
4. B树的性能优化
高效的磁盘I/O操作
- 批量操作:在插入和删除操作中,尽量减少磁盘I/O次数。例如,批量插入或删除数据。
- 缓存机制:利用缓存机制,将常用的节点保存在内存中,减少磁盘访问次数。
- 预读和延迟写:在读取数据时,可以采用预读策略,一次读取多个节点数据;在写入数据时,可以采用延迟写策略,减少写入次数。
内存优化
- 节点大小设计:设计合适的节点大小,以充分利用内存和磁盘空间。通常,节点大小与磁盘块大小一致,能够提高磁盘I/O效率。
- 压缩存储:对节点中的键值和指针进行压缩存储,减少内存占用。
- 内存池管理:使用内存池管理节点对象,减少频繁的内存分配和释放,提高内存使用效率。
并行化与并发控制
- 读写锁机制:使用读写锁机制,允许多线程同时读取,提高查询并发性能。在写操作时,使用写锁,确保数据一致性。
- 分区锁机制:将树分成多个分区,每个分区独立加锁,减少锁竞争,提高并发性能。
- 多线程构建:在构建B树时,采用多线程并行构建,提高构建速度。
5. B树的应用场景与案例分析
数据库系统
B树广泛应用于数据库系统中的索引结构,如MySQL的InnoDB存储引擎使用B+树作为默认的索引结构。通过B树,数据库能够高效地进行数据插入、删除和查找操作。
文件系统
文件系统中也大量使用B树进行目录和文件的管理。例如,ReiserFS文件系统使用B树来存储文件和目录,提高文件系统的性能和稳定性。
具体案例分析
MySQL中的B+树索引
MySQL的InnoDB存储引擎使用B+树作为默认的索引结构。每个B+树节点包含一个页,页的大小通常为16KB。B+树中的每个节点存储多个键值和指针,通过页的链表实现有序存储。在查询过程中,通过B+树的层级结构快速定位目标数据,提高查询性能。
ReiserFS文件系统
ReiserFS文件系统使用B树来管理文件和目录。通过B树,文件系统能够高效地进行文件查找、插入和删除操作。ReiserFS还使用了日志机制,确保文件系统的可靠性和数据一致性。
6. 源码解析
B树的基本操作源码分析
以下是B树的基本操作(插入、删除、查找)的源码解析:
插入操作
插入操作通过递归实现,在插入过程中进行节点分裂,保持树的平衡。
void BTree::insert(int k) {if (root == nullptr) {root = new BTreeNode(t, true);root->keys[0] = k;root->n = 1;} else {if (root->n == 2*t-1) {BTreeNode *s = new BTreeNode(t, false);s->C[0] = root;s->splitChild(0, root);int i = 0;if (s->keys[0] < k)i++;s->C[i]->insertNonFull(k);root = s;} elseroot->insertNonFull(k);}
}
删除操作
删除操作通过递归实现,在删除过程中进行节点合并和键值借用,保持树的平衡。
void BTree::remove(int k) {if (!root) {cout << "The tree is empty\n";return;}root->remove(k);if (root->n == 0) {BTreeNode *tmp = root;if (root->leaf)root = nullptr;elseroot = root->C[0];delete tmp;}
}
查找操作
查找操作通过递归实现,在节点中查找目标键值,如果未找到,则递归查找子节点。
BTreeNode* BTreeNode::search(int k) {int i = 0;while (i < n && k > keys[i])i++;if (keys[i] == k)return this;if (leaf)return nullptr;return C[i]->search(k);
}
平衡性维护源码解析
在插入和删除操作中,B树通过节点分裂、节点合并和键值借用等机制,自动维护树的平衡。具体的平衡性维护源码已经在前文中详细介绍,不再重复。
性能优化源码解析
以下是一些性能优化的源码示例,包括批量操作、缓存机制和并行化构建等。
批量插入操作
批量插入操作通过减少磁盘I/O次数,提高插入性能。
void BTree::bulkInsert(vector<int> keys) {for (int k : keys)insert(k);
}
缓存机制
缓存机制通过将常用节点保存在内存中,减少磁盘访问次数。
class BTreeCache {
public:unordered_map<int, BTreeNode*> cache;BTreeNode* getNode(int id) {if (cache.find(id) != cache.end())return cache[id];// 从磁盘加载节点BTreeNode *node = loadFromDisk(id);cache[id] = node;return node;}void putNode(int id, BTreeNode *node) {cache[id] = node;}
};
并行化构建
并行化构建通过多线程提高B树的构建速度。
void BTree::parallelBuild(vector<int> keys) {int n = keys.size();#pragma omp parallel forfor (int i = 0; i < n; i++)insert(keys[i]);
}
7. 总结
B树作为一种高效的平衡多叉树数据结构,广泛应用于数据库和文件系统中。通过自动平衡机制,B树能够在插入和删除操作中保持树的平衡,确保高效的查找性能。通过合理的性能优化策略,如批量操作、缓存机制和并行化构建,可以进一步提高B树的性能。本文详细介绍了B树的平衡性和性能优化策略,并通过源码解析提供了深入的理解。希望能够帮助读者更好地理解和应用B树,提高系统性能。
相关文章:

B树的平衡性与性能优化
B树的平衡性与性能优化 B树(B-tree)是一种自平衡的树数据结构,广泛应用于数据库和文件系统中,用于保持数据的有序性并允许高效的插入、删除和查找操作。B树能够很好地处理大规模数据,并在磁盘I/O操作中表现出色。本文…...

llama3源码解读之推理-infer
文章目录 前言一、整体源码解读1、完整main源码2、tokenizer加载3、llama3模型加载4、llama3测试数据文本加载5、llama3模型推理模块1、模型推理模块的数据处理2、模型推理模块的model.generate预测3、模型推理模块的预测结果处理6、多轮对话二、llama3推理数据处理1、完整数据…...

【教程】Linux安装Redis步骤记录
下载地址 Index of /releases/ Downloads - Redis 安装redis-7.4.0.tar.gz 1.下载安装包 wget https://download.redis.io/releases/redis-7.4.0.tar.gz 2.解压 tar -zxvf redis-7.4.0.tar.gz 3.进入目录 cd redis-7.4.0/ 4.编译 make 5.安装 make install PREFIX/u…...

全球汽车线控制动系统市场规模预测:未来六年CAGR为17.3%
引言: 随着汽车行业的持续发展和对安全性能需求的增加,汽车线控制动系统作为提升车辆安全性和操控性的关键组件,正逐渐受到市场的广泛关注。本文旨在通过深度分析汽车线控制动系统行业的各个维度,揭示行业发展趋势和潜在机会。 【…...

Ubuntu运行深度学习代码,代码随机epoch中断没有任何报错
深度学习运行代码直接中断 文章目录 深度学习运行代码直接中断问题描述设备信息问题补充解决思路问题发现及正确解决思路新问题出现最终问题:ubuntu系统,4090显卡安装英伟达驱动535.x外的驱动会导致开机无法进入桌面问题记录 问题描述 运行深度学习代码…...

只有4%知道的Linux,看了你也能上手Ubuntu桌面系统,Ubuntu简易设置,源更新,root密码,远程服务...
创作不易 只因热爱!! 热衷分享,一起成长! “你的鼓励就是我努力付出的动力” 最近常提的一句话,那就是“但行好事,莫问前程"! 与辉同行的董工说:守正出奇。坚持分享,坚持付出,坚持奉献,…...
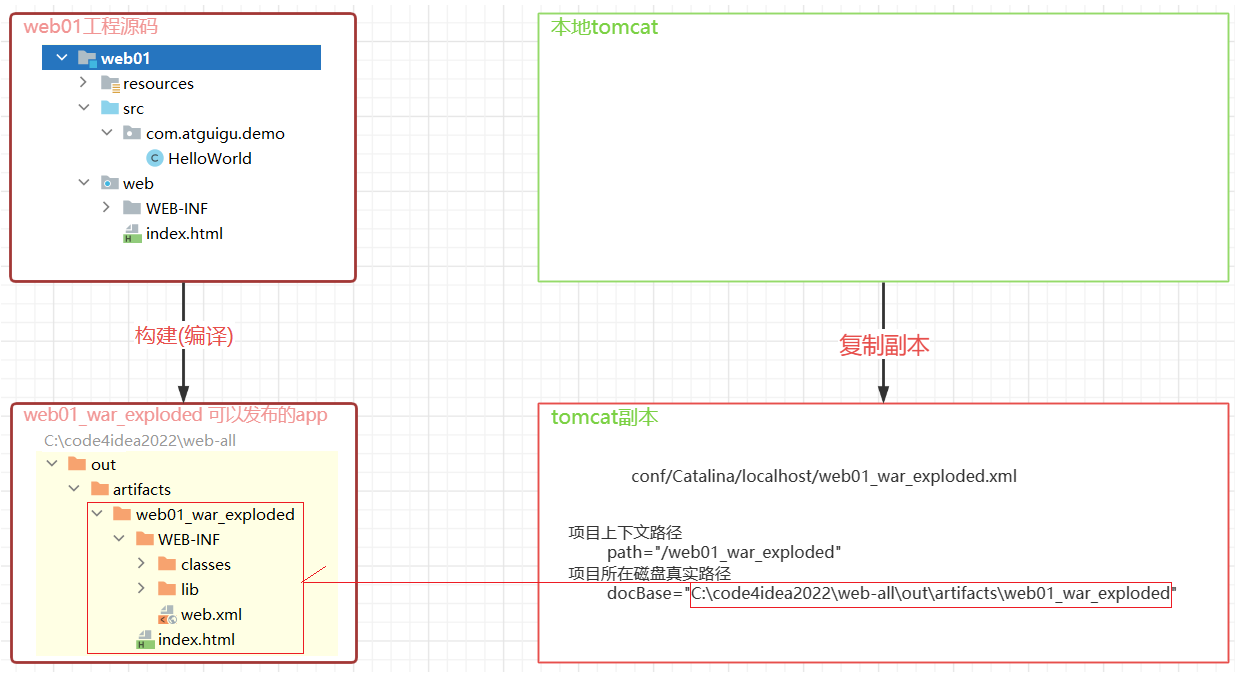
Tomcat部署——个人笔记
Tomcat部署——个人笔记 文章目录 [toc]简介安装配置文件WEB项目的标准结构WEB项目部署IDEA中开发并部署运行WEB项目 本学习笔记参考尚硅谷等教程。 简介 Apache Tomcat 官网 Tomcat是Apache 软件基金会(Apache Software Foundation)的Jakarta 项目中…...

常见且重要的用户体验原则
以下是一些常见且重要的用户体验原则: 1. 以用户为中心 - 深入了解用户的需求、期望、目标和行为习惯。通过用户研究、调查、访谈等方法获取真实的用户反馈,以此来设计产品或服务。 - 例如,在设计一款老年手机时,充分考虑老年…...

web基础及nginx搭建
第四周 上午 静态资源 根据开发者保存在项目资源目录中的路径访问静态资源 html 图片 js css 音乐 视频 f12 ,开发者工具,网络 1 、 web 基本概念 web 服务器( web server ):也称 HTTP 服务器( HTTP …...

C++ 布隆过滤器
1. 布隆过滤器提出 我们在使用新闻客户端看新闻时,它会给我们不停地推荐新的内容,它每次推荐时要去重,去掉 那些已经看过的内容。问题来了,新闻客户端推荐系统如何实现推送去重的? 用服务器记录了用 户看过的所有历史…...

使用HTML创建用户注册表单
在当今数字化时代,网页表单对于收集用户信息和促进网站交互至关重要。无论您设计简单的注册表单还是复杂的调查表,了解HTML的基础知识可以帮助您构建有效的用户界面。在本教程中,我们将详细介绍如何使用HTML创建基本的用户注册表单。 第一步…...

Python零基础入门教程
Python零基础详细入门教程可以从以下几个方面进行学习和掌握: 一、Python基础认知 1. Python简介 由来与发展:Python是一种广泛使用的高级编程语言,由Guido van Rossum(吉多范罗苏姆)于1991年首次发布。Python以其简…...

成为git砖家(10): 根据文件内容生成SHA-1
文章目录 1. .git/objects 目录2. git cat-file 命令3. 根据文件内容生成 sha-14. 结语5. References 1. .git/objects 目录 git 是一个根据文件内容进行检索的系统。 当创建 hello.py, 填入 print("hello, world")的内容, 并执行 git add hello.py gi…...

园区导航小程序:一站式解决园区导航问题,释放存储,优化访客体验
随着园区的规模不断扩大,功能区划分日益复杂,导致访客和新员工在没有有效导航的情况下容易迷路。传统APP导航虽能解决部分问题,但其下载安装繁琐、占用手机内存大、且非高频使用导致的闲置,让许多用户望而却步。园区导航小程序的出…...
)
对于n进制转十进制的解法及代码(干货!)
对于p进制转十进制,我们有:(x)pa[0]*p^0a[1]*p^1a[2]*p^2...a[n]*p^n 举个例子:(11001)21*10*20*41*81*1625 (9FA)1610*16^015*16^19*16^22554 据此,我们可以编出c代码来解决问题 …...

当代互联网打工人的生存现状,看完泪流满面!
欢迎私信小编,了解更多产品信息呦~...

花几千上万学习Java,真没必要!(三十八)
测试代码1: package iotest.com; import java.nio.charset.StandardCharsets; import java.io.UnsupportedEncodingException; public class StringByteConversion { public static void main(String[] args) throws UnsupportedEncodingException { // 原始字…...

Zilliz 2025届校园招聘正式启动,寻找向量数据库内核开发工程师
为了解决非结构化数据处理问题,我们构建了向量数据库-Milvus! Milvus 数据库不仅是顶级开源基金会 LF AI&Data 的毕业项目,还曾登上数据库顶会SIGMOD、VLDB,在全球首届向量检索比赛中夺冠。目前,Milvus 项目已获得超过 2.8w s…...

TwinCAT3 新建项目教程
文章目录 打开TwinCAT 新建项目(通过TcXaeShell) 新建项目(通过VS 2019)...

大模型算法面试题(十九)
本系列收纳各种大模型面试题及答案。 1、SFT(有监督微调)、RM(奖励模型)、PPO(强化学习)的数据集格式? SFT(有监督微调)、RM(奖励模型)、PPO&…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...
