C++ 布隆过滤器
1. 布隆过滤器提出
我们在使用新闻客户端看新闻时,它会给我们不停地推荐新的内容,它每次推荐时要去重,去掉 那些已经看过的内容。问题来了,新闻客户端推荐系统如何实现推送去重的? 用服务器记录了用 户看过的所有历史记录,当推荐系统推荐新闻时会从每个用户的历史记录里进行筛选,过滤掉那 些已经存在的记录。 如何快速查找呢?
1. 用哈希表存储用户记录,缺点:浪费空间
2. 用位图存储用户记录,缺点:位图一般只能处理整形,如果内容编号是字符串,就无法处理了。
3. 将哈希与位图结合,即布隆过滤器
2. 布隆过滤器概念
布隆过滤器是由布隆(Burton Howard Bloom)在1970年提出的一种紧凑型的、比较巧妙的概率型数据结构,特点是高效地插入和查询,可以用来告诉你 “某样东西一定不存在或者可能存在”,它是用多个哈希函数,将一个数据映射到位图结构中。此种方式不仅可以提升查询效率,也可以节省大量的内存空间。
、
3. 布隆过滤器的实现代码
#include<iostream>
#include<bitset>
using namespace std;
//哈希函数
struct BKDRHash
{size_t operator()(const string& s){// BKDRsize_t value = 0;for (auto ch : s){value *= 31;value += ch;}return value;}
};
struct APHash
{size_t operator()(const string& s){size_t hash = 0;for (long i = 0; i < s.size(); i++){if ((i & 1) == 0)hash ^= ((hash << 7) ^ s[i] ^ (hash >> 3));elsehash ^= (~((hash << 11) ^ s[i] ^ (hash >> 5)));}return hash;}
};
struct DJBHash
{size_t operator()(const string & s){size_t hash = 5381;for (auto ch : s){hash += (hash << 5) + ch;}return hash;}
};
//第一个参数为插入的个数,第二个参数为容器要开空间为插入个数的倍数大小,
//第三个参数为插入的元素类型,后三个参数为哈希函数
template<size_t N,size_t X = 5,class K = string,class Hash1= BKDRHash,class Hash2 = APHash, class Hash3 = DJBHash >
class BloomFilter
{
public:void set(const K& key){size_t len = N * X;size_t index1 = Hash1()(key) % len;size_t index2 = Hash2()(key) % len;size_t index3 = Hash3()(key) % len;_bitset.set(index1);_bitset.set(index2);_bitset.set(index3);}bool test(const K& key){size_t len = N * X;size_t index1 = Hash1()(key) % len;if (_bitset.test(index1) == false)return false;size_t index2 = Hash2()(key) % len;if (_bitset.test(index2) == false)return false;size_t index3 = Hash3()(key) % len;if (_bitset.test(index2) == false)return false;return true;}private:bitset<N* X> _bitset;
};3.1 布隆过滤器的插入
假设我们要插入元素x,使用三个哈希函数分别计算元素x,得到三个位置。将这三个位置的值从0改为1。

3.2 布隆过滤器的查找
3.3 布隆过滤器删除
4.布隆过滤器的优缺点
5.布隆过滤器的应用场景
布隆过滤器广泛应用于各种计算机系统中,用于提高数据处理的效率和减少不必要的磁盘或网络I/O操作。一些典型的应用场景包括:
-
缓存穿透防护:在分布式缓存系统中,布隆过滤器可以用来检测一个请求的键是否可能存在于缓存中,从而避免不必要的数据库查询。
-
网络爬虫:布隆过滤器可以帮助网络爬虫避免重复访问同一个URL。
-
垃圾邮件过滤:通过维护一个包含已知垃圾邮件特征的布隆过滤器,可以快速过滤掉疑似垃圾邮件。
-
社交网络内容过滤:布隆过滤器可以用来避免向用户推荐他们已经查看过的内容。
-
数据库优化:在数据库中,布隆过滤器可以用来减少对不存在的行或列的查找,从而提高查询效率。
相关文章:

C++ 布隆过滤器
1. 布隆过滤器提出 我们在使用新闻客户端看新闻时,它会给我们不停地推荐新的内容,它每次推荐时要去重,去掉 那些已经看过的内容。问题来了,新闻客户端推荐系统如何实现推送去重的? 用服务器记录了用 户看过的所有历史…...

使用HTML创建用户注册表单
在当今数字化时代,网页表单对于收集用户信息和促进网站交互至关重要。无论您设计简单的注册表单还是复杂的调查表,了解HTML的基础知识可以帮助您构建有效的用户界面。在本教程中,我们将详细介绍如何使用HTML创建基本的用户注册表单。 第一步…...

Python零基础入门教程
Python零基础详细入门教程可以从以下几个方面进行学习和掌握: 一、Python基础认知 1. Python简介 由来与发展:Python是一种广泛使用的高级编程语言,由Guido van Rossum(吉多范罗苏姆)于1991年首次发布。Python以其简…...

成为git砖家(10): 根据文件内容生成SHA-1
文章目录 1. .git/objects 目录2. git cat-file 命令3. 根据文件内容生成 sha-14. 结语5. References 1. .git/objects 目录 git 是一个根据文件内容进行检索的系统。 当创建 hello.py, 填入 print("hello, world")的内容, 并执行 git add hello.py gi…...

园区导航小程序:一站式解决园区导航问题,释放存储,优化访客体验
随着园区的规模不断扩大,功能区划分日益复杂,导致访客和新员工在没有有效导航的情况下容易迷路。传统APP导航虽能解决部分问题,但其下载安装繁琐、占用手机内存大、且非高频使用导致的闲置,让许多用户望而却步。园区导航小程序的出…...
)
对于n进制转十进制的解法及代码(干货!)
对于p进制转十进制,我们有:(x)pa[0]*p^0a[1]*p^1a[2]*p^2...a[n]*p^n 举个例子:(11001)21*10*20*41*81*1625 (9FA)1610*16^015*16^19*16^22554 据此,我们可以编出c代码来解决问题 …...

当代互联网打工人的生存现状,看完泪流满面!
欢迎私信小编,了解更多产品信息呦~...

花几千上万学习Java,真没必要!(三十八)
测试代码1: package iotest.com; import java.nio.charset.StandardCharsets; import java.io.UnsupportedEncodingException; public class StringByteConversion { public static void main(String[] args) throws UnsupportedEncodingException { // 原始字…...

Zilliz 2025届校园招聘正式启动,寻找向量数据库内核开发工程师
为了解决非结构化数据处理问题,我们构建了向量数据库-Milvus! Milvus 数据库不仅是顶级开源基金会 LF AI&Data 的毕业项目,还曾登上数据库顶会SIGMOD、VLDB,在全球首届向量检索比赛中夺冠。目前,Milvus 项目已获得超过 2.8w s…...

TwinCAT3 新建项目教程
文章目录 打开TwinCAT 新建项目(通过TcXaeShell) 新建项目(通过VS 2019)...

大模型算法面试题(十九)
本系列收纳各种大模型面试题及答案。 1、SFT(有监督微调)、RM(奖励模型)、PPO(强化学习)的数据集格式? SFT(有监督微调)、RM(奖励模型)、PPO&…...

应用地址信息获取新技巧:Xinstall来助力
在移动互联网时代,应用获取用户地址信息的需求越来越普遍。无论是为了提供个性化服务,还是进行精准营销,地址信息都扮演着至关重要的角色。然而,如何合规、准确地获取这一信息,却是许多开发者面临的挑战。今天…...

图的最短路径算法:Dijkstra、Floyd-Warshall、Bellman-Ford
本文意在探讨图中最短路径算法 Dijkstra、Floyd-Warshall、Bellman-Ford 的对比和细节 整体分为如下四部分 总结性的比较了 Dijkstra、Floyd-Warshall、Bellman-FordDijkstra 算法介绍Floyd-Warshall 算法介绍Bellman-Ford 算法介绍 其中1、2、3 算法介绍部分会比较简洁&…...
)
Camera的pipline(TODO)
(TODO)...

非关系数据库-非关系数据库入门指南
非关系数据库入门指南 1. 引言:非关系数据库的兴起 在互联网技术飞速发展的今天,传统的关系型数据库面对海量数据和高并发访问时逐渐显得力不从心。于是,非关系数据库(NoSQL,Not Only SQL)应运而生&…...
)
看门狗IWDG、WWDG(速记版)
内置的看门狗有 独立看门狗 IWDG 和 窗口看门狗 WWDG 都用来在程序卡死的时候复位程序。 独立看门狗只有一个最晚时间界限。窗口看门狗有一个最早界限和最晚界限。独立看门狗有独立的时钟,一般设置来源时钟LSI40KHz。窗口看门狗挂靠在APB1总线上36MHz。 IWDG IWDG处于VDD供…...

ETL工程师角度下的SQL优化
作为ETL(Extract, Transform, Load)工程师,SQL优化是提高数据处理和分析效率的关键一环。优化SQL查询可以显著降低数据处理时间,提高ETL过程的性能。本文将从 合理设计数据模型:在ETL过程中,正确的数据模型…...
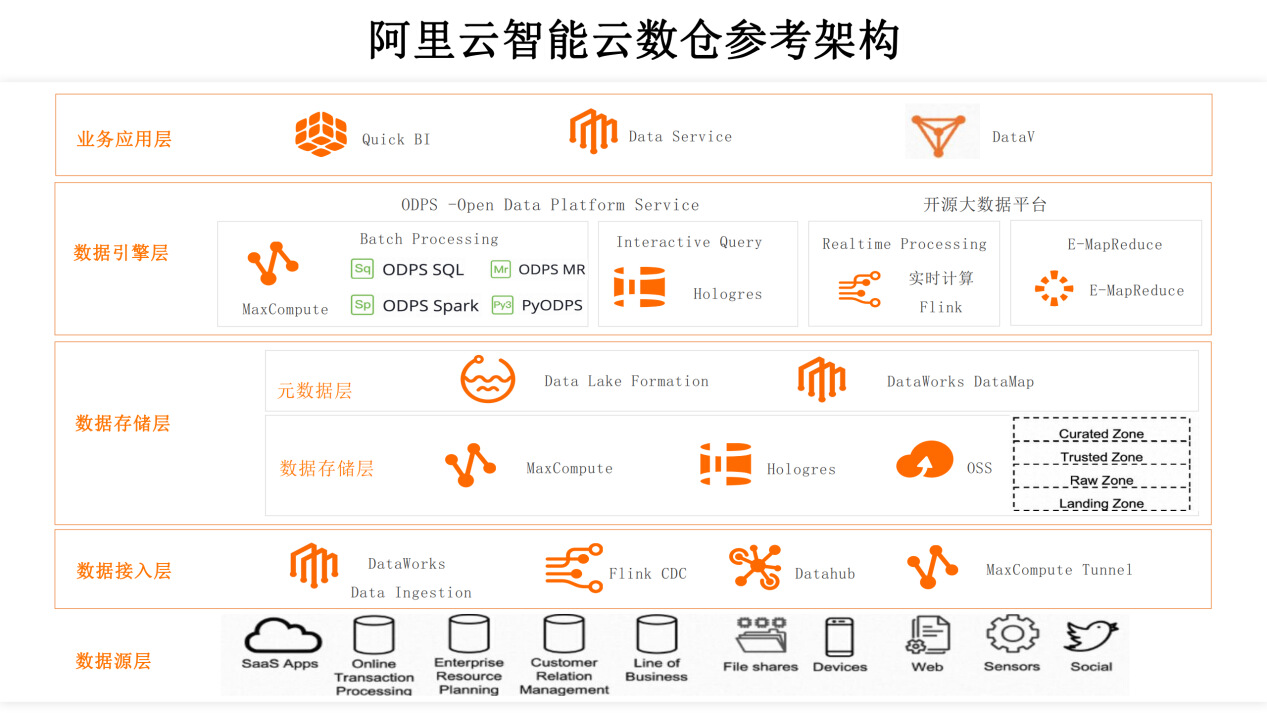
阿里云实时计算Flink在多行业的应用和实践
摘要:本文整理自 Flink Forward Asia 2023 中闭门会的分享。主要分享实时计算在各行业的应用实践,对回归实时计算的重点场景进行介绍以及企业如何使用实时计算技术,并且提供一些在技术架构上的参考建议。内容分为以下四个部分: 业…...
)
开源项目与工具:C++中的高性能并发库 - Intel Threading Building Blocks (TBB)
在C++的世界里,随着多核处理器成为常态,如何有效利用这些多核资源以实现高性能的并发编程成为了开发者们关注的焦点。Intel Threading Building Blocks (TBB) 作为一个专为并行编程设计的C++库,凭借其易用性、高效性和可扩展性,在高性能计算、游戏开发、金融分析等多个领域…...

Chapter 22 数据可视化——折线图
欢迎大家订阅【Python从入门到精通】专栏,一起探索Python的无限可能! 文章目录 前言一、Pyecharts介绍二、安装Pyecharts三、全局配置项四、绘制折线图 前言 在大数据时代,数据可视化成为了分析和展示数据的重要手段。Pyecharts 是一个基于 …...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...
