泛化的最近点迭代法(Generalized-ICP)
Generalized-ICP算法是由斯坦福大学的Aleksandr V. Segal、Dirk Haehnel和Sebastian Thrun提出的,于2009年在Robotics science and system会议上发表。
GICP是一种ICP算法的变体,其原理与ICP算法相同,之所以称为泛化的ICP算法是因为大多数ICP框架没有被修改,仍用kd树检索临近点以保持速度和简单性,GICP所提出的泛化只处理目标函数的迭代计算,对收敛函数进行优化,将协方差矩阵计算加入误差函数。
GICP是一种ICP算法的变体,其原理与ICP算法相同,之所以称为泛化的ICP算法是因为大多数ICP框架没有被修改,仍用kd树检索临近点以保持速度和简单性,GICP所提出的泛化只处理目标函数的迭代计算,对收敛函数进行优化,将协方差矩阵计算加入误差函数。

其标准算法可以分为两步: (a)确定两组点云之间的点的对应关系; (b)计算一个使对应点之间的距离最小化的变换;

ICP算法核心的核心部分在伪码的第五行:在点云A中查找R·bi + t的对应点,为了保持算法的简单性,选择欧式距离最小的点作为对应点; 第七行:寻找最佳的将R·bi + t变换到mi的变换函数。这里最佳变化函数通过使一个特定的损失函数最小化确定,这个损失函数的不同也是本节提到的三种算法的根本区别。
ICP算法有很多变体,其中point-to-plane的变体利用表面法线信息提高了性能。在标准ICP算法中,通过迭代使得对应点的欧氏距离即∑▒||R·b_i+t−m_i||^2最小化,但point-to-plane变体中,是使源表面上的点沿目标表面的曲面法线投影到切平面子空间上的误差最小化,如图,源表面上的点s1沿目标表面上的点d1的法线方向l1投影到d1的切平面上,投影点到d1的距离即为所求误差。


这一变化是通过改变标准ICP算法Algorithm 1中的第5行完成的,其中表示mi的曲面法线:

而GICP则是在这一步对目标函数的迭代估计上引入了概率模型,但是对应点的查找仍然使用欧式距离,而非概率度量,从而仍能使用kd树来查找最近点,保持了ICP相对于其他完全依赖概率模型的算法的主要优势——速度和简单性。 假设点云A={ai}和B={bi}(i=1,...,n)是已经完成对应点匹配的两个点云,即ai与bi是对应点。建立一种点云概率模型,假设存在一组潜在的点A ̂={(a_i) ̂}和B ̂={(b_i) ̂}符合高斯分布,且点ai和点bi是从和中选取,即:
![]()
![]()
ai和bi是点(a_i) ̂和(b_i) ̂的真实位置,{C_i^A}和{C_i^B}是已知的协方差矩阵。定义残差d_i^R,t=b_i− R·a_i−t,则有:

对于真实位置的变换(R*,t*)则有:

接下来通过最大似然估计法(Maximum Likelihood Estimation, MLE)对R*和t*进行估计,则有最大似然函数:

由于上式不是凸函数,不便求其最大值,所以将(R,t)放在协方差中再利用MLE进行估算,将优化问题简化为最小化损失函数:

其中,M_i=(C_i^B+RC_i^AR^T)^−1 上式即是GICP算法的核心内容。容易发现当令{C_i^A}=0和{C_i^B}=1时,得到的正是标准ICP的算式,即标准ICP算法是泛化ICP算法的一种特殊情况。
在这种形式下也简化了梯度计算,用r_i表示残差,即r_i=b_i−R·a_i−t,梯度可以表示为:

由于这是一个约束优化问题,R必须是一个旋转矩阵,所以不能使用共轭梯度下降来解决。引入欧拉参数对旋转矩阵R进行描述,欧拉参数化的优点是使用了三个独立的参数(θ_x,θ_y,θ_z)。
由于这是一个约束优化问题,R必须是一个旋转矩阵,所以不能使用共轭梯度下降来解决。引入欧拉参数对旋转矩阵R进行描述,欧拉参数化的优点是使用了三个独立的参数(θ_x,θ_y,θ_z)。

则有R相对于θ的梯度:

通过链式规则,有:

GICP中使用的点云协方差矩阵与传统的点云协方差矩阵的定义不同,由于现实物体表面是分段可微的,因此GICP假设数据集是局部平面的,即点服从平面分布,每个采样点在其局部平面方向上分布的协方差很高,而在曲面法线方向上分布的协方差很低。则可以设计一个模型,使得点在法线方向具有较小的方差,设为,值为0.001;在平面方向具有较大的方差,设为1:

这里的R_ni是一个旋转矩阵,将基底向量e1旋转到点的法线方向。实际计算中,这个旋转矩阵是通过计算该点附近的点的协方差矩阵,并进行奇异值分解(Singular Value Decomposition,SVD)得到的,即为Σ ̂=UDU^T中的矩阵U。

相关文章:

泛化的最近点迭代法(Generalized-ICP)
Generalized-ICP算法是由斯坦福大学的Aleksandr V. Segal、Dirk Haehnel和Sebastian Thrun提出的,于2009年在Robotics science and system会议上发表。 GICP是一种ICP算法的变体,其原理与ICP算法相同,之所以称为泛化的ICP算法是因为大多数ICP…...

Java | Leetcode Java题解之第313题超级丑数
题目: 题解: class Solution {public int nthSuperUglyNumber(int n, int[] primes) {int[] dp new int[n 1];int m primes.length;int[] pointers new int[m];int[] nums new int[m];Arrays.fill(nums, 1);for (int i 1; i < n; i) {int minN…...

单细胞数据整合-去除批次效应harmony和CCA (学习)
目录 单细胞批次效应学习 定义 理解 常用的去批次方法-基于Seurat 1) Seurat-integration(CCA) 2) Seurat-harmony 去批次代码 ①Seurat-integration(CCA) ②Seurat-harmony 单细胞批次效应学习 …...

MuRF代码阅读
对图像Size的处理, 以适应Transformer 在MVSPlat 当中使用 Center_Crop 裁剪图像,适用于 Transformer 的32 倍数, 其中 焦距 f 不变化,只改变 cx,cy.MuRF 直接对图像进行 插值,合成理想的 size. 根据 ori_size 和 inference_size…...

pycharm无法导入pyside2模块;“ModuleNotFoundError: No module named ‘PySide2“
参考博客: 1)pycharm中配置pyqt designer和pyside2【功能是在pycharm中可以打开designer,并且可以把.ui文件转换为.py文件】 https://blog.csdn.net/kuntliu/article/details/117219237 2).ui转化为.py后,点击运行,报错…...

c语言指针中“数组名的理解”以及“一维数组传参”的本质
数组名的理解 数组名就是数组首元素的地址。 例如:输入一个数组的所有元素,再打印出来。 另一种写法 以上可以看出:*arri) arr[i] 也即是:*(iarr)i[arr] 本质上无区别 1:数组就是数组,是一块…...

计算机毕业设计Python+Flask微博舆情分析 微博情感分析 微博爬虫 微博大数据 舆情监控系统 大数据毕业设计 NLP文本分类 机器学习 深度学习 AI
基于Python/flask的微博舆情数据分析可视化系统 python爬虫数据分析可视化项目 编程语言:python 涉及技术:flask mysql echarts SnowNlP情感分析 文本分析 系统设计的功能: ①用户注册登录 ②微博数据描述性统计、热词统计、舆情统计 ③微博数…...
KubeBlocks v0.9 解读|最高可管理 10K 实例的 InstanceSet 是什么?
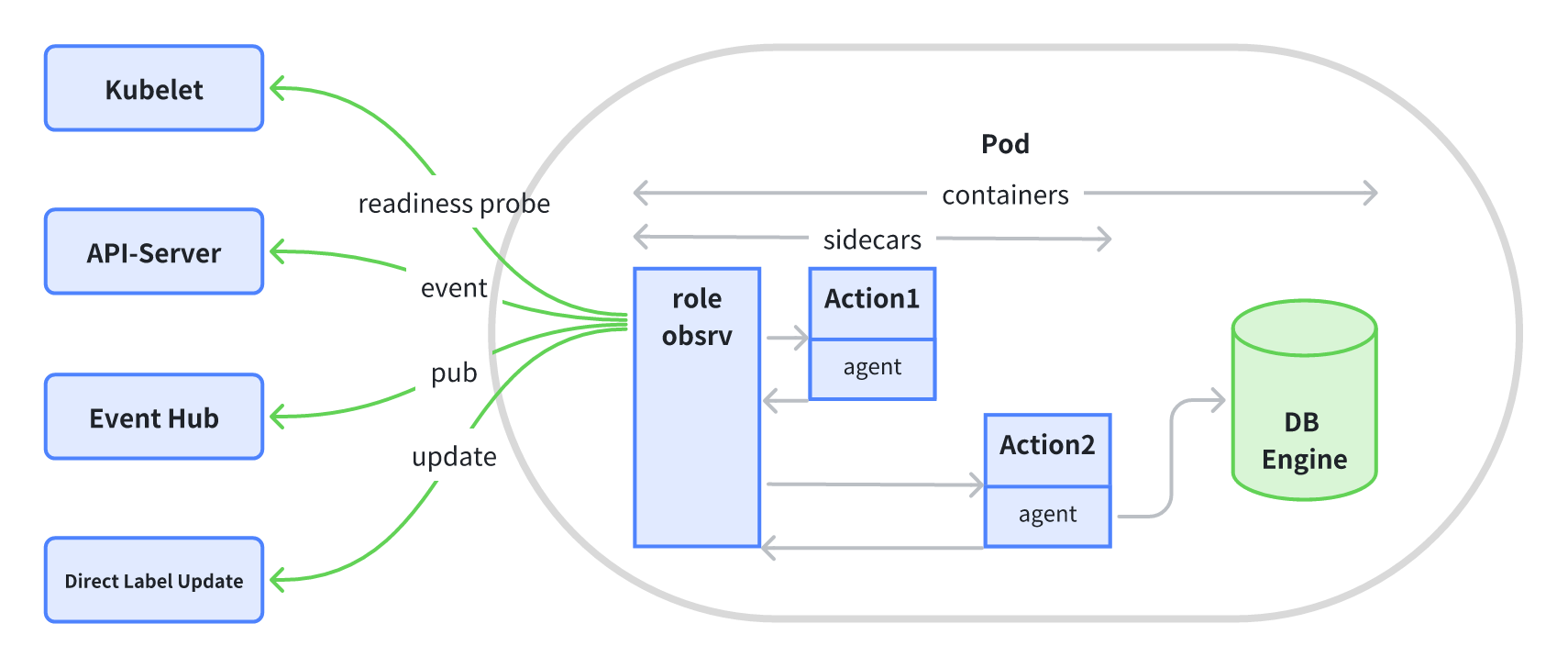
实例(Instance)是 KubeBlocks 中的基本单元,它由一个 Pod 和若干其它辅助对象组成。为了容易理解,你可以先把它简化为一个 Pod,下文中将统一使用实例这个名字。 InstanceSet 是一个通用 Workload API,负责…...

ZW3D二次开发_菜单_禁用/启用表单按钮
1.如图示,ZW3D可以禁用表单按钮(按钮显示灰色) 2.禁用系统默认表单按钮,可以在菜单空白处右击,点击自定义,找到相关按钮的名称,如下图。 然后使用代码: char name[] "!FtAllBo…...

windows子系统wsl完成本地化设置locale,LC_ALL
在 Windows 的子系统 Linux(WSL)环境中,解决本地化设置问题可以采取以下步骤: 1. **检查本地化设置**: 打开你的 WSL 终端(比如 Ubuntu、Debian 等),运行以下命令来查看当前的本…...

MYSQL 根据条件order by 动态排序
文章目录 案例1:根据动态值的不同,决定某个字段是升序还是降序案例2:根据动态值的不同,决定使用哪个字段排序 最近在做大数据报表时,遇到这样一种情况,若是A类型,则部门按照正序排序;…...

DirectX修复工具下载安装指南:电脑dll修复拿下!6种dll缺失修复方法!
在日常使用电脑的过程中,不少用户可能会遇到“DLL文件缺失”的错误提示,这类问题往往导致程序无法正常运行或系统出现不稳定现象。幸运的是,DirectX修复工具作为一款功能强大的系统维护软件,能够有效解决大多数DLL文件缺失问题&am…...
虚拟数字键盘的封装,(2)以及子组件改变父组件变量的值进而使子组件实时响应值的变化,(3)子组件调用父组件中的方法(带参))
vue3(1)虚拟数字键盘的封装,(2)以及子组件改变父组件变量的值进而使子组件实时响应值的变化,(3)子组件调用父组件中的方法(带参)
父组件 <template><div><!-- 数字键盘 --><NumericKeyboardv-model:myDialogFormVisible"myDialogFormVisible" :myValueRange"myValueRange"submit"numericKeyboardSubmitData"/></div> </template><s…...

反序列化靶机serial
1.创建虚拟机 2.渗透测试过程 探测主机存活(目标主机IP地址) 使用nmap探测主机存活或者使用Kali里的netdicover进行探测 -PS/-PA/-PU/-PY:这些参数即可以探测主机存活,也可以同时进行端口扫描。(例如:-PS࿰…...

扎克伯格说Meta训练Llama 4所需的计算能力是Llama 3的10倍
Meta 公司开发了最大的基础开源大型语言模型之一 Llama,该公司认为未来将需要更强的计算能力来训练模型。马克-扎克伯格(Mark Zuckerberg)在本周二的 Meta 第二季度财报电话会议上表示,为了训练 Llama 4,公司需要比训练…...

CTFHUB-文件上传-双写绕过
开启题目 1.php内容: <?php eval($_POST[cmd]);?> 上传一句话木马 1.php,抓包,双写 php 然后放包,上传成功 蚁剑连接 在“/var/www/html/flag_484225427.php”找到了 flag...

RabbitMQ docker部署,并启用MQTT协议
在Docker中部署RabbitMQ容器并启用MQTT插件的步骤如下: 一、准备工作 安装Docker: 确保系统上已安装Docker。Docker是一个开源的容器化平台,允许以容器的方式运行应用程序。可以在Docker官方网站上找到适合操作系统的安装包,并…...

Python面试宝典第25题:括号生成
题目 数字n代表生成括号的对数,请设计一个函数,用于能够生成所有可能的并且有效的括号组合。 备注:1 < n < 8。 示例 1: 输入:n 3 输出:["((()))","(()())","(())()"…...

计算机毕业设计选题推荐-社区停车信息管理系统-Java/Python项目实战
✨作者主页:IT研究室✨ 个人简介:曾从事计算机专业培训教学,擅长Java、Python、微信小程序、Golang、安卓Android等项目实战。接项目定制开发、代码讲解、答辩教学、文档编写、降重等。 ☑文末获取源码☑ 精彩专栏推荐⬇⬇⬇ Java项目 Python…...

Python面试整理-自动化运维
在Python中,自动化运维是一个重要的应用领域。Python凭借其简单易用的语法和强大的库支持,成为了运维工程师的首选工具。以下是一些常见的自动化运维任务以及如何使用Python来实现这些任务: 1. 文件和目录操作 Python的os和shutil模块提供了丰富的文件和目录操作功能。 impo…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...

嵌入式常见 CPU 架构
架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集,单周期执行;低功耗、CIP 独立外设;用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel(原始…...
